基于三角形面积的航迹降采样算法∗

陆 遥 刘雪娇 鲁爱国

（1.武汉数字工程研究所 武汉 430205）（2.91977部队 北京 100036）

1 引言

随着现代通讯协议和通讯设备的发展，运动目标的航迹数据监测变得越来越容易。已经有很多研究者探讨了如何利用ADS-B 系统采集飞行数据［1］或利用AIS 系统采集船舶数据［2］，如何解读这些报文信息，如何应用特定规则处理时间戳误差［3］，如何利用卡尔曼滤波等经典算法清洗异常数据［4］以及如何利用各种聚类算法研究不同目标的航迹之间的关联性［5］。

本文将关注航迹数据的展示环节。在有限的用户屏幕空间内显示过多的航迹历史点，可能会导致整体图像看起来非常杂乱，尤其是当被监视的目标没有固定的运动路线或是采取了大量机动动作时。

包含高密度的数据点分布的折线图无法向图表的观察者提供有效的信息。在部分片段上，多个历史点迹绘制在过于接近的屏幕位置上，因此很难确定飞行目标的运动状态和未来趋势。例如，如果在相对较小的画布上绘制1000个数据点，如图1所示，最终会得到这种类型的历史航迹图。

图1 包含1000个历史点迹的航迹数据（模拟生成）

在将大量航迹历史点迹可视化为图像时，如果想要看清整个图表，则须采取一些必要步骤来避免前面讨论的问题。在目标运动模式相对简单的场景下，可以取一些原始数据点的平均值作为新的数据点来表示原始数据的缩略效果。为了实现这一效果，可以应用例如回归分析等众所周知的方法。

然而，本文算法设计的重点在于探索使用原始数据中存在的数据点作为子集的降采样算法。最简单的办法即是根据历史点迹的数据量和画布的大小，仅使用每隔十个数据点或可能间隔更多取数据点作为原始数据的代表。不过，这种方法仅适用于原始数据平滑且波动很小的情况。如果原始数据的波动幅度巨大，那么使用上述方法绘制的图像会损失原始数据中的许多视觉特征，如图2 所示。显然，航迹数据展示环节需要一种更合适的降采样算法，这就是本文的写作目的。

图2 对图1每隔10个历史点迹保留1个点

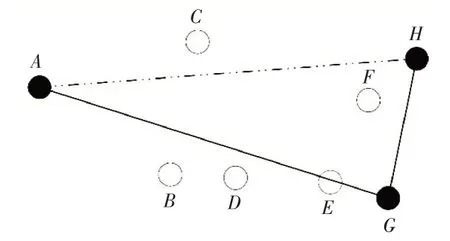
图3 点G距离直线AH最远

需要强调的是，降采样后的数据仅用于直观地表示原始数据的特征以供用户观察，而不是用于数据分析、统计或其他任务。在处理视觉表示的信息时，只保留提供最多可被人为感知的特征的数据点很重要，其余的数据点可以丢弃。因此，数据分析领域的算法的一部分评估指标可能不适用于评价降采样算法。

2 相关工作分析

在对船舶AIS 航迹信息或飞行器ADS-B 航迹信息的数据采集、清洗和处理分析的许多相关文章中，有一部分讨论了如何压缩保存海量的原始数据，这些作者采用了几种不同的航迹简化办法。

2.1 最小描述长度准则

对于已经确定的航迹数据，可以利用特定的编码模型对其进行数据压缩。为了正确还原航迹原始数据，需要将压缩后的数据和所用的编码模型保存起来。需要保存的数据长度即为原始航迹数据被编码压缩后的数据长度和编码模型的数据长度，其被称为总描述长度。最小描述长度准则［6］即需要寻找总描述长度最小的编码模型。

肖潇［7］把航向和航速变化超过阈值的点筛选为特征点，再提出了最小描述长度准则的开销计算公式，进一步筛选关键点。

2.2 自适应航迹拟合压缩算法

考虑到运动目标在大多时候处于平稳运动状态，速度、航向和高度变化很小，因此可以在运动目标的平稳运动阶段采用三次函数拟合其轨迹，而保留爬升、下降或变速阶段的关键航迹点，最终只需要存储原始航迹中的变化关键点和平稳状态的拟合多项式系数。

梁复台［8］利用迭代逼近的方法寻找拟合误差最小的航迹分段方式，将其中速度及高度保持稳定的分段用三次函数拟合，将其余分段的航迹信息保留，即使将一段特定的航迹压缩至7%，仍可以使压缩后的航迹与原始航迹拟合误差小于0.0001。

2.3 Douglas-Peucker算法

Douglas-Peucker 算法［9］是制图领域中针对折线简化的经典算法，其先在轨迹折线的首尾两点之间连接一条直线AH，然后求折线上的其他所有点到直线AH 的距离，找到距离最远的点G，将距离记为dmax；比较该距离dmax与预先定义的阈值D 大小，如果dmax

张树凯［10］对琼海海峡的AIS 数据应用了不同阈值的Douglas-Peucker 算法，将航迹点数量压缩至原始数据的15%仍可以取得与原始数据类似的显示效果。

2.4 Visvalingam-Whyatt算法

Visvalingam-Whyatt算法［11］是另一种制图领域中专门简化折线的算法。该算法背后的基本思想是根据一个点与前后的两个相邻点形成的三角形的面积大小赋予其重要性等级，这通常记作该点的有效面积。根据有效面积去除原始数据中最不重要的点，被去除的点的相邻点需要重新计算有效面积，然后再次执行该算法直到所有剩余的点的有效面积超过预先设定的阈值。例如，图4 中F 点的有效面积EFG 比其余都小，优先删除F 点，此后相邻点E的有效面积从DEF变为DEG。

图4 相邻点组成的三角形EFG面积最小

秦育罗［12］利用Visvalingam-Whyatt算法简化了海南省的海岸线地图点迹，在原始数据压缩至24%时仍可以不丢失原始细节。

3 算法改进设计

现有的航迹降采样算法可以在保证误差极小的前提下对静态存储的航迹数据做到极高的压缩效率，但这些现有算法的时间效率都不是太理想，即使是效率最高的Visvalingam-Whyatt算法的时间复杂度也为O（n log（n））。在部分需要实时展示最新航迹数据的场景下，提高降采样算法的时间效率是非常必要的任务，为此可以牺牲一部分误差率，只要求降采样后的航迹图像保留原始视觉特征即可。本文将在Visvalingam-Whyatt算法的思想基础上以提升时间效率为目标改进算法作为新的航迹降采样算法。

3.1 分段并行的Visvalingam-Whyatt算法

这个算法思路非常简单。首先将原始航迹数据平均分组，例如将1000 个点降采样为200 个点时，则每组均有5 个点。然后仿照Visvalingam-Whyatt 算法的第一步计算每个点与前后两点组成的三角形面积大小作为每个点的重要性，对同一个组内的所有点进行重要性排名（需要排除有效面积为空的点）。最后，选择每个分组内排名最高的点（最大有效区域）来表示降采样后的数据。

如图5 所示，点B、点C、点D 被分到同一个分组内，因为B点与相邻两点组成的三角形ABC面积比三角形BCD 或三角形CDE 更大，所以降采样后的数据将选择B点作为该分组的代表点。

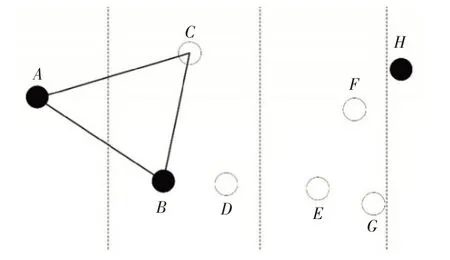
图5 B点的有效面积在其分组内最大

图6 对图1采用算法1降采样至100个点

算法1 分段并行的Visvalingam-Whyatt算法

输入参数：原始数据点，降采样后的点数量m

1：将原始数据点的首尾两点作为降采样后的首尾点

2：将剩余的原始数据点平均分为m-2组

3：在每一个分组内：

计算每个点与前后两点组成的三角形面积

选择面积最大的点作为该组的代表点

4：将首尾点和每一组的代表点作为降采样后的数据点

该算法对于航迹点迹的取舍仅仅取决于每个点与前后点组成的三角形面积，因此在保证了时间复杂度为O（n）的前提下，在一定程度上保留原始数据中的“突变”点，而“突变点”是对于航迹图像观察者在视觉上最为显著的特征。

3.2 远视的Visvalingam-Whyatt改进算法

3.1节中的算法在计算一个点的有效面积时只考虑这个点前后的两个相邻点，这在大多数情况下都可以完成降采样任务，但如果原始航迹数据中存在大量分布不均匀的跳点时，3.1 节中的算法可能存在问题。此时原始数据中某两个航迹点的时间距离大于其余点之间的时间距离，也即这两个点之间的物理距离可能远大于其余点之间的物理距离，这将导致跳点附近航迹点的有效面积远大于其他点。以往的算法可能会尝试利用现有数据补全原始航迹数据中的跳点，但为提升算法的时间效率和存储效率，本文尝试采用一种更为巧妙的优化办法。

一个明显的解决思路是能否让一个点的有效面积更大，并且在某种意义上让每一组内选择的点更具有长期代表性？本节将讨论与3.1节类似的算法，但此算法中一个点的有效面积不取决于它的两个相邻点的位置，而是取决于上一个和下一个分组中的点，使得该点的有效面积所表示的特征区域大得多也更具有长期代表性。

第一步与算法1 相同，也是将所有数据点平均分成数量相等的分组。同样地，将原始数据点的起始点和结束点作为降采样后的起始点和结束点。

下一步是从左到右依次遍历从第一个到最后一个分组，在每一个分组内选择一个点，该点应与前一个分组的代表点和后一个分组的代表点组成的三角形面积最大。

计算形成上述的三角形面积时，左侧的第一个点始终固定为上一个分组的代表点，中间的点为当前的分组中的一个点，需要通过遍历求出。问题是从下一个分组中选择哪一个点来形成三角形。

显而易见的答案是使用蛮力方法并简单地尝试所有可能性。即对于当前分组中的每个点，与下一个分组中的所有点形成一个三角形，显然这种蛮力做法效率低下，不可能应用于实际生产环境中。例如，如果要将1000个原始数据点降采样为100个点，则算法共计需要计算大约10000 次三角形的面积。更高效的解决方案是在下一个分组中添加一个虚拟点作为下一个分组的代表。这样需要计算的三角形的数量只等于原始数据的点数，然后选择当前分组中与左右两个固定点形成面积最大的三角形的点。图7 中显示了B 点、C 点、D 点被分到同一个分组，其中C 点与固定点A（之前分组选择的）和虚拟点X 形成的三角形ACX 面积比三角形ABX或三角形ADX更大，所以这一分组内将选择C点作为代表点。

图7 C点与A点和虚拟点X组成的三角形在其分组内最大

图8 对图1采用算法2降采样至100个点

图9 包含1000个点的原始数据图像（即图1）

图10 每隔20个点保留一个点的降采样结果

图11 采用算法1降采样至50个点

图12 采用算法2降采样至50个点

下一个分组中的这个虚拟点应该如何决定的问题仍然存在。一个简单的想法是使用下一个分组中的所有点的平均值。经过实验在大多数情况下，这与蛮力方法降采样后的图像一样有效，但效率更高。

算法2 远视的Visvalingam-Whyatt改进算法

输入参数：原始数据点，降采样后的点数量m

1：将原始数据点的首尾两点作为降采样后的首尾点

2：将剩余的原始数据点平均分为m-2组

3：在每一个分组内：

计算下一个分组的所有点的坐标平均值

计算每个点与前一个分组的代表点和下一个分组的平均点组成的三角形面积

选择面积最大的点作为该组的代表点

4：将首尾点和每一组的代表点作为降采样后的数据点

4 极端降采样比例下的结果对比

上述几种算法在常规的降采样任务中得到的最终图像非常相近，时间复杂度均为O（n），满足了实时展示航迹数据场景下的降采样需求。但在极端条件下，即降采样后的数据点与原始数据点的数量比例下降到一个极小值时，两者产生的图像会产生些许不同。

经过实际测试，在包含不规则变化的连续数据集上进行降采样时，如果用少于原始数量5%的点表示原始图像时，不管采取何种高效算法或暴力算法，都会大幅度损失其原始数据的变化特征。因此，本文比较了降采样比例恰好为5%的情况下各算法生成的图像。

显然算法2 在降采样比例低至5%时更能保留原始数据的图像特征。作为时间复杂度O（n）的算法，算法2 是同等运行时间条件下降采样效果最好的算法。

5 结语

本论文的主要目标是设计和实现一些可以对航迹数据进行降采样的高效率的算法，以产生保留数据特征的视觉简化表示，然后比较这些算法以确定哪些是最实用的。事实证明，算法2 在大多数情况下能够高效地产生良好的结果。但对包含大量平滑区间的航迹数据采用平均分组的降采样算法，在极端的降采样比例下无论如何取舍原始点都会损失大量图形特征，后续工作将探讨根据原始航迹数据的运动特征进行不平均分组的降采样算法。