不同注浆压力下采空区浆液扩散规律研究
2023-11-15程立朝李新旺郝云德王海璇
程立朝,路 滨,李新旺,郝云德,龙 杭,王海璇
(1.河北工程大学矿业与测绘工程学院,河北邯郸 056038;2.河北工程大学 河北省高校煤炭资源开发与建设应用技术研发中心,河北 邯郸 056038;3.河北工程大学 邯郸市煤基固废规模化利用技术创新中心,河北 邯郸 056038)
0 引 言
煤炭开采规模的不断扩大,导致地表形成大面积的沉陷区,地表生态环境出现破坏[1]。采空区充填注浆是近年发展起来的生态保护性开采技术,采空区注浆加固治理是一种通过地面打孔渗透注浆实现采空区沉降改善的治理工艺[2-3]。通过将特定性质的材料配制成浆液,借由地面提前钻孔布设的注浆管,在一定的压力下将浆液注入采空区地基矸石堆体内,通过浆液的渗透实现采空区充填。随后,浆液经过胶凝或固化处理,促使地基的物理力学性质得到改善,从而达到加固采空区地表地基的目的。渗透注浆作为一种有效的施工方法,在工程领域具有广泛的应用前景。
在对采空区渗透注浆扩散规律的相关研究中,国内外学者已经进行了大量的工作。杨志全[4]等基于宾汉姆流体浆液时变性的流变方程和渗流运动过程,得到了浆液时变性对注浆扩散半径的影响规律;阮文军[5]通过大量的试验研究,建立了不同流形浆液的粘度时变性方程,在此基础上获得了稳定的水泥浆液注浆扩散模型;李术才[6]等研究了基于黏度时变性的双液浆液扩散运移机制;黄河飞[7]利用COMSOL 探究了水灰比、注浆压力等对浆液扩散渗透规律的影响;尚宏波[8]等利用COMSOL 构建了地面下含水层帷幕注浆浆液扩散物理模型,讨论了在动水条件下浆液扩散范围影响因素;刘洋[9]等通过COMSOL 建立在岩石裂隙中注浆扩散模型,研究了粘度及裂隙粗糙度对扩散半径的影响;钱自卫[10]等基于达西定律推算出全新的渗透注浆浆液扩散半径公式;张宏图[11]等基于COMSOL 中流固耦合模块,研究了不同注浆压力下瓦斯抽采水泥砂浆封孔注浆扩散模型,讨论了砂浆黏度变化对注浆影响;王庆磊[12]等基于渗滤效应的多孔介质探究了低渗透率宾汉姆浆液渗透扩散规律;Maghous 等[13]分析了水泥浆液在多孔介质中径向流动时出现的过滤现象;杨文才研究获得了基于浆液自重的牛顿、宾汉姆和幂律流体的球形渗透注浆理论[14];朱明听[15]利用CFD 中的COMSOL 软件,在单一裂隙注浆扩散为背景下,采用理论分析与数值模拟相结合的方法,通过控制变量包括注浆压力、注浆速度和裂隙开度等,模拟了浆液扩散运移和注浆压力在不同流场下的分布规律。这些学者的研究工作丰富了采空区渗透注浆扩散规律的理论基础。他们通过试验、理论推导和数值模拟等手段,对不同类型的注浆流体和工程情况进行了深入的研究。这些研究成果对于优化渗透注浆工程的设计参数、预测注浆效果,以及提高工程施工质量,具有重要意义。通过进一步深入研究和探索,能够更好地理解和应用采空区渗透注浆扩散规律,提升了采空区治理的效果和安全性。
当前国内外学者在注浆浆液扩散规律方面展开了大量的研究,但多以Magg 球状扩散理论和达西定律为主,对于在浅埋深大面积采空区注浆工程中,注浆在杂乱矸石堆中扩散规律鲜有研究。因此,本文旨在以宾汉姆粉煤灰浆液为研究基础,考虑宾汉姆粉煤灰浆液的黏度特性、流动性以及与土层矸石堆的相互作用等因素,对其在采空区内复杂的流动扩散规律进行研究,以提供一定的理论基础来指导实际的注浆工程。
1 采空区内渗透注浆浆液扩散物理模型
1.1 水泥粉煤灰浆液流变方程
在对采空区内水泥粉煤灰浆液渗透扩散机理进行研究时,可对采空区提出以下假设。
(1)注浆治理的采空区内被注煤矸石和冒落岩石散体是一种均匀和各向同性的多孔介质,被注散体各个方向性质相同。
(2)水泥粉煤灰浆液可被视为不可压缩的流体,同时其自身也是均质且各向同性。此外,浆液粘度随时间发生变化,这种变化关系可以用指数函数来描述。而在整个注浆过程中,水泥粉煤灰浆液的屈服应力整体上保持不变。
(3)采用填压法进行注浆,通过注浆管口将水泥粉煤灰浆液注入采空区被注介质内。
(4)浆液流动速度较小,除了在注浆孔周围局部区域,浆液的流态呈现紊流状态外,其余部分表现为层流。
以Brinkman 方程为研究基础,认为水泥粉煤灰浆液遵循宾汉姆流体流动特性,满足流变方程:
式中:τ 为剪切应力,Pa;τ0为屈服应力,Pa;μn为塑性粘度,Pa·S;γ 为剪切速率(γ=-),S-1。
水泥粉煤灰浆液的粘度时变性规律为:
式中:μno为水泥粉煤灰浆液初始粘度值,Pa·s;μn为浆液时变粘度值,Pa·S;k 为粘度时变系数;t为注浆时间,S。
式(1)、式(2)联立可得水泥粉煤灰浆液考虑粘度时变性状况下的流变方程:
1.2 宾汉姆流体渗流扩散规律
当研究宾汉姆流体在圆管中的层流流动时,可以考虑在圆管内取一段以管轴为对称轴的流体柱,其长度取dl,半径取r<r0,r0为圆管半径,如图1所示。

图1 水泥粉煤灰浆液在圆管中的流动示意Fig.1 Flowdiagram of cement fly ash slurry in circular tube
在不考虑重力对其流动影响下,该流体柱力学平衡公式为:
流体柱微元部dl 两端的压力分别为p+dp 和p,两端压差为dp。流体柱元素表面上受剪切应力为τ,其方向向左与流速方向相反。可以得到剪应力τ:
在柱元素表面上,剪切应力τ 与柱元素半径r和压力梯度dp/dl 的乘积成正比,但符号相反。将上式带入宾汉姆流变方程可得水泥粉煤灰浆液的渗流运动方程为:
式中:v 为水泥粉煤灰浆液渗流速度,m/s;K 为地层渗透系数;α 为水的渗透系数。
由v=q/A 可得:
积分可得:
根据边界条件p=p1时,l=l0;p=p0时,l=l0可以计算出浆液扩散半径:
2 采空区注浆浆液扩散数值模拟
2.1 控制方程
采空区注浆浆液扩散过程本质上是水泥粉煤灰浆液驱替其他物质的过程。采空区内有大量冒落的矸石和其他岩体,其松散堆积体可以视为多孔介质,孔隙率一般都比较大,故选择COMSOL 中的Brinkman 方程对采空区内浆液扩散效果进行模拟。
(1)运动控制方程。
Brinkman 方程是一种在多孔介质流动中考虑渗流和粘流耦合效应的方程。该方程描述了在多孔介质中流动的动量守恒和连续性。第一项表示速度的散度,第二项表示速度的扩散,第三项表示速度的粘性耗散,第四项表示压力梯度,最后一项表示外部施加的力场。
式中:εp为孔隙率;K 为渗透系数;Qm为流量。
2.2 模型建立及边界设定
以邯邢地区浅埋深煤层采空区为研究背景,数值模拟模型设定为100 m×100 m×4 m,工作面平均厚度为4 m,注浆管直径为10 cm,注浆管位于模型的中心位置,整个模型采取自由形三角形单元进行划分,为了提高计算的精确度,在注浆管口处网格进行加密处理。网格划分如图2 所示。

图2 模型概图Fig.2 Model overview
模型的四周边界均为无滑移,入口边界设定为压力入口,注浆压力为p_in=0.2 MPa,出口边界为p=0,冒落矸石堆孔隙率为0.302 6,水泥粉煤灰的密度为1 342 kg/m3,数值模拟参数见表1。

表1 计算参数Table 1 Calculation parameters
水泥粉煤灰浆液的时变性曲线如图3 所示。

图3 粘度时变性曲线Fig.3 Viscosity time-varying curve
2.3 浆液扩散数值模拟结果和分析
在用COMSOL MULTIPHYSICS 模拟水泥粉煤灰浆液在采空区冒落矸石堆中流动扩散规律时,可以用浓度指标来表示注浆浆液的扩散范围,可以认为浓度达到0.1 以上时,浆液可以到达这些地方,即为浆液扩散区域。
2.3.1 注浆时间对扩散半径的影响
在进行注浆时,由于水泥粉煤灰浆液具有黏度时变性,故研究浆液扩散随时间变化的趋势,截取不同时间点的扩散形态图,其它参数保持不变。模拟结果如图4 所示。

图4 注浆时间对浆液扩散距离的影响Fig.4 Effect of grouting time on slurry diffusion distance
观察结果表明,水泥粉煤灰浆液在模拟实验中以注浆管为中心以圆状进行扩散,这可以归因于对被注入的矸石堆采用各向同性假设。根据这个假设,浆液从注浆孔流出后在各个方向上的扩散距离是相等的,因此导致了浆液以相同速率扩散至各个方向。在以下描述中,圆形区域表示了浆液在采空区内的扩散距离:对于注浆时间为2 h 的情况(图4a),浆液的扩散距离达到了6.93 m;对于注浆时间为4 h 的情况(图4b),扩散距离增至8.27 m;对于注浆时间为6 h 的情况(图4c),浆液的扩散距离为9.15 m;在注浆时间为8 h 的情况下(图4d),浆液的扩散距离扩展至9.95 m。
上述数据可以整理成图5,显示了不同注浆时间下浆液扩散距离的变化趋势。这一趋势清晰地展示了浆液扩散随着注浆时间变化的关系。
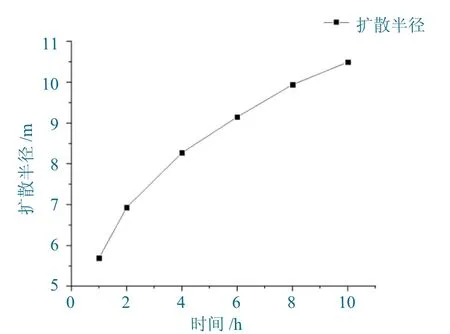
图5 扩散距离与时间的关系Fig.5 The relationship between diffusion distance and time
由图5 可知:
(1)在进行采空区注浆加固的初期,由于采空区内孔隙率较大,随着注浆时间的增大,水泥粉煤灰浆液扩散半径也随之增加。
(2)浆液的流动扩散速度随着浆液扩散的位置越远而逐渐减小,这是因为浆液的粘度随着时间的增加而增大,到一定时刻,浆液的粘度无限大后,浆液停止流动。因此对于采空区注浆加固来说,注浆时间对于水泥粉煤灰浆液扩散半径的影响主要取决于浆液何时凝固。
2.3.2 注浆压力对扩散半径的影响
注浆压力是指在注浆过程中施加到浆液上的力,使浆液能够克服地下介质的阻力,渗透进入孔隙或裂缝中。注浆压力的大小对注浆效果具有重要影响,过低的压力可能导致浆液无法充分渗透,而过高的压力则可能引起地下介质的破坏或浆液四溢,造成浆液浪费。查阅有关规定,此次模拟注浆压力主要选取0.2~1 MPa。
在保证其他条件不变的情况下,改变注浆压力。模拟结果如图6 所示。

图6 注浆压力对浆液扩散距离的影响Fig.6 Effect of grouting pressure on slurry diffusion distance
图6(a)展示了在0.2 MPa 注浆压力下,浆液的扩散情况,结果显示浆液最终的扩散范围达到10.01 m;而图6(b)呈现了在0.5 MPa 注浆压力下,浆液在介质中的扩散情况,相应扩散距离为14.51 m;图6(c)呈现了在1 MPa 注浆压力下浆液的扩散状况,浆液最终的扩散距离达到18.96 m。图中圆圈内区域为浆液的最大流速区域,而圆圈外区域则代表浆液流速为零的区域。
由图6 可以看出:
(1)在相同的注浆材料、冒落矸石堆孔隙率下,不同情况的浆液扩散半径随着注浆压力增大而增大。
(2)注浆压力的增加会导致浆液的初始流动速度增大。当水泥粉煤灰浆液在采空区内矸石堆孔隙流动时,克服孔隙水压力和颗粒之间的阻力等会导致浆液动能损失,从而引起流速逐渐减小。当浆液的初始流动速度较大时,这种流速减缓的趋势较为缓和,因此在采空区内的扩散半径越大。
为研究在注浆过程中,不同区域压力的变化,在离注浆管口1、2、3 m 的高度布设3 条注浆压力测线,线上均匀布设监测点,如图7 所示。不同距离压力变化如图8 所示。

图7 监测点布设Fig.7 layout of monitoring spot

图8 不同距离压力变化Fig.8 Pressure variation at different heights
从图8 可以看出,在同一深度,压力值在注浆管中心位置,同一高度压力在注浆管中心附近压力值最大,压力随着水泥粉煤灰浆液扩散范围的增大而向边界递减,在深度越大的位置,注浆渗透压力的值越小,变化幅度越小,距离注浆管越远的地方压力增加速度越慢,说明注浆压力对距离越远的测点影响越弱。
3 结 论
(1)水泥粉煤灰浆液属于宾汉姆流体,在注浆过程中其粘度存在时变性,粘度随时间发生指数型变化。
(2)水泥粉煤灰浆液在采空区内扩散形态最初呈球体变化至圆柱体;浆液扩散半径随着注浆时间增加而增大,且变化速度随着浆液粘度的增大而减小。
(3)注浆扩散距离随着时间的增大而增加,由于粘度时变性的影响,扩散速度随之减少。注浆压力对浆液扩散范围影响较为明显,随着注浆压力的增大,浆液扩散距离随之增大,可以得出,在前期注浆的时候可以提供较小的压力,可适当地提高注浆压力来提高注浆效率。
