基于关键刀轴矢量插值的球头铣刀五轴加工光顺刀轴矢量生成方法
2023-11-15卢耀安丘洪键王成勇
卢耀安 丘洪键 王成勇
1.广东工业大学机电工程学院,广州,5100062.广东省微创手术器械设计与精密制造重点实验室,广州,5100063.高性能工具全国重点实验室,广州,510006
0 引言
与三轴机床相比,五轴机床在加工灵活性方面具有明显的优势,这些优势来自五轴机床的两个旋转轴,它使刀具能够以不同姿态切触零件表面,切削过程更容易避免碰撞干涉。选取合适的刀轴矢量可以提高加工带宽和材料去除率[1]、减小加工振动[2]等。复杂曲面类零件主要是指由复杂曲线、曲面组成的形状复杂、曲面曲率变化大的零件。球头铣刀由于其几何自适应性好,被广泛应用于复杂曲面类零件加工。
五轴铣削加工过程中,刀轴矢量可能存在突变。刀轴矢量突变所需的加减速度可能会超出机床旋转轴的驱动极限,造成加工过程不平稳,在加工表面留有刀具痕迹,直接影响零件表面加工质量,甚至会发生过切。刀轴矢量突变还会造成刀具破损。工件坐标系的刀轴矢量与机床旋转轴角度位置间的非线性变换关系导致工件坐标系下光顺的刀轴矢量不代表加工时机床旋转轴会平稳运动[3]。在机床坐标系下优化刀轴矢量可以使机床旋转轴运动平稳,避免旋转轴频繁地加减速。规划机床旋转轴运动平稳的刀轴矢量首先要保证刀轴矢量无碰撞干涉。刀具-工件-机床间碰撞干涉情况的复杂性导致刀轴矢量可行域边界复杂,如凹区域、不连通区域等,难以用解析式表示复杂的可行域边界。许多学者对刀轴矢量可行域形状进行简化[4-5],然后优化刀轴矢量,但得到的结果可能不是全局最优结果。
目前的刀轴矢量光顺优化研究在加工路径各刀触点刀轴矢量可行域内采样刀轴矢量,然后通过限制机床坐标系下相邻刀轴矢量之间的变化获得光顺的刀轴矢量。PLAKHOTNIK等[6]将刀具前倾角作为优化变量,以整个加工路径的机床旋转轴角度位置变化总和最小为目标,采用最短路径算法获得光顺的刀轴矢量。MI等[7]首先以可行刀轴矢量为顶点、机床旋转轴运动速度为边权重构造有向图,然后提出了差分有向图构造方法,使用最短路径算法求解该差分有向图获得光顺的刀轴矢量,该方法不仅可以考虑机床旋转轴运动速度还可以考虑旋转轴运动加速度。后来,他们以降低机床旋转轴运动加速度和提高切削宽度为目标,使用最短路径算法求解差分有向图获得曲面边界光顺的刀轴矢量,然后采用双线性曲面插值法获得整个曲面的刀轴矢量序列[1]。使用最短路径算法求解光顺刀轴矢量生成问题,若想要获取质量较好的结果,刀轴矢量可行域的采样间隔需要控制得很小,此时可行刀轴矢量个数增多,使用最短路径算法求解光顺刀轴矢量生成问题会需要较长的运行时间[8]。针对最短路径算法求解光顺刀轴矢量问题运行时间长的难题,笔者提出了缩短使用最短路径算法求解光顺刀轴矢量问题运行时间的策略,生成了鼓形铣刀五轴铣削加工刀具路径[9]。GONG等[10]提出了一种基于直纹面空间的五轴铣削加工刀轴矢量优化方法,该方法根据原始刀轴矢量生成直纹面空间,以最小化机床旋转轴角度位置变化为目标优化该直纹面的控制点,最终获得光顺刀轴矢量。为降低球头铣刀刀轴矢量的改变对刀具路径各刀触点处的刀具-工件接触区域的影响,WANG等[5]提出了新的光顺刀具路径生成方法,但该方法的不足之处是它需要简化刀轴矢量可行域形状。
上述光顺刀轴矢量生成研究都是针对整个加工路径各刀触点的刀轴矢量,这些方法需要计算加工路径各刀触点处刀轴矢量可行域,耗费了大量的内存空间和计算时间。基于关键刀轴矢量(representative tool orientation, RTO)插值的刀轴矢量优化方法使刀轴矢量光顺优化和碰撞干涉检查解耦,避免计算整个加工路径各刀触点处刀轴矢量可行域,可缩短光顺刀轴矢量生成时间。该方法首先设定初始的关键刀轴矢量序列,然后插值这些关键刀轴矢量序列获得整个加工路径的刀轴矢量序列,然后进行碰撞干涉检查,如果发生碰撞干涉,则在碰撞干涉区域选择一个可行刀轴矢量作为新关键刀轴矢量,并添加到关键刀轴矢量序列,然后重新插值关键刀轴矢量序列并重复上述步骤,直到加工路径的刀轴矢量序列不发生碰撞干涉。HO等[11]采用球面四元数法插值关键刀轴矢量序列生成加工路径的刀轴矢量序列,随后对存在碰撞干涉的区域添加新关键刀轴矢量,重新插值关键刀轴矢量序列并且重复上述步骤,最终获得无碰撞干涉的光顺刀轴矢量序列。XU等[12]根据关键刀轴矢量序列计算整个加工路径的刀轴矢量序列,然后找出发生碰撞干涉的区域以及刀触点位置,在其可行域边界上搜索与原刀轴矢量夹角最小的新可行刀轴矢量。在每个发生碰撞干涉的区域选取令上述夹角最大的可行刀轴矢量作为该区域的新关键刀轴矢量,然后再计算整个加工路径的刀轴矢量序列。重复上述步骤,最终获得整个加工路径无碰撞干涉的光顺刀轴矢量。后来,他们还提出了在机床坐标系内对刀轴矢量进行局部光顺性修正的方法[13]。
基于关键刀轴矢量插值的刀轴矢量优化方法需设定初始的关键刀轴矢量序列。初始的关键刀轴矢量序列会直接影响整个加工路径的刀轴矢量序列,然而,现有文献直接指定初始关键刀轴矢量序列(文献[11-12]指定加工路径首末两个刀位处刀轴矢量作为初始关键刀轴矢量),较少研究如何合理选择初始关键刀轴矢量序列。优化后的加工路径刀轴矢量序列是否仍存在碰撞干涉、光顺性是否达到要求,这些都与关键刀轴矢量序列选取是否合理有关[14]。然而,在迭代过程,现有方法根据已有的关键刀轴矢量序列选择新的关键刀轴矢量,然后在后续迭代过程中固定这些关键刀轴矢量,缺乏关键刀轴矢量序列整体优化方法,这样会影响整个加工路径刀轴矢量序列的整体光顺性。针对以上问题,本文提出了基于贪心策略的关键刀轴矢量序列整体优化方法,进而提出基于关键刀轴矢量插值的球头铣刀五轴加工复杂曲面光顺刀轴矢量生成方法,该方法对机床旋转轴运动进行光顺优化,使机床旋转轴运动平稳。
1 五轴加工刀具路径基础
1.1 球头铣刀刀位计算
如图1所示,在刀触点O处建立局部坐标系{O;XL,YL,ZL},其中XL与刀触点轨迹线在O处的单位切向量一致,ZL与曲面在O处的单位外法向量一致,YL=ZL×XL。刀具在局部坐标系{O;XL,YL,ZL}的刀轴矢量可以用绕YL旋转的前倾角λ和绕XL旋转的侧倾角ω描述,于是,单位刀轴矢量T可表示为
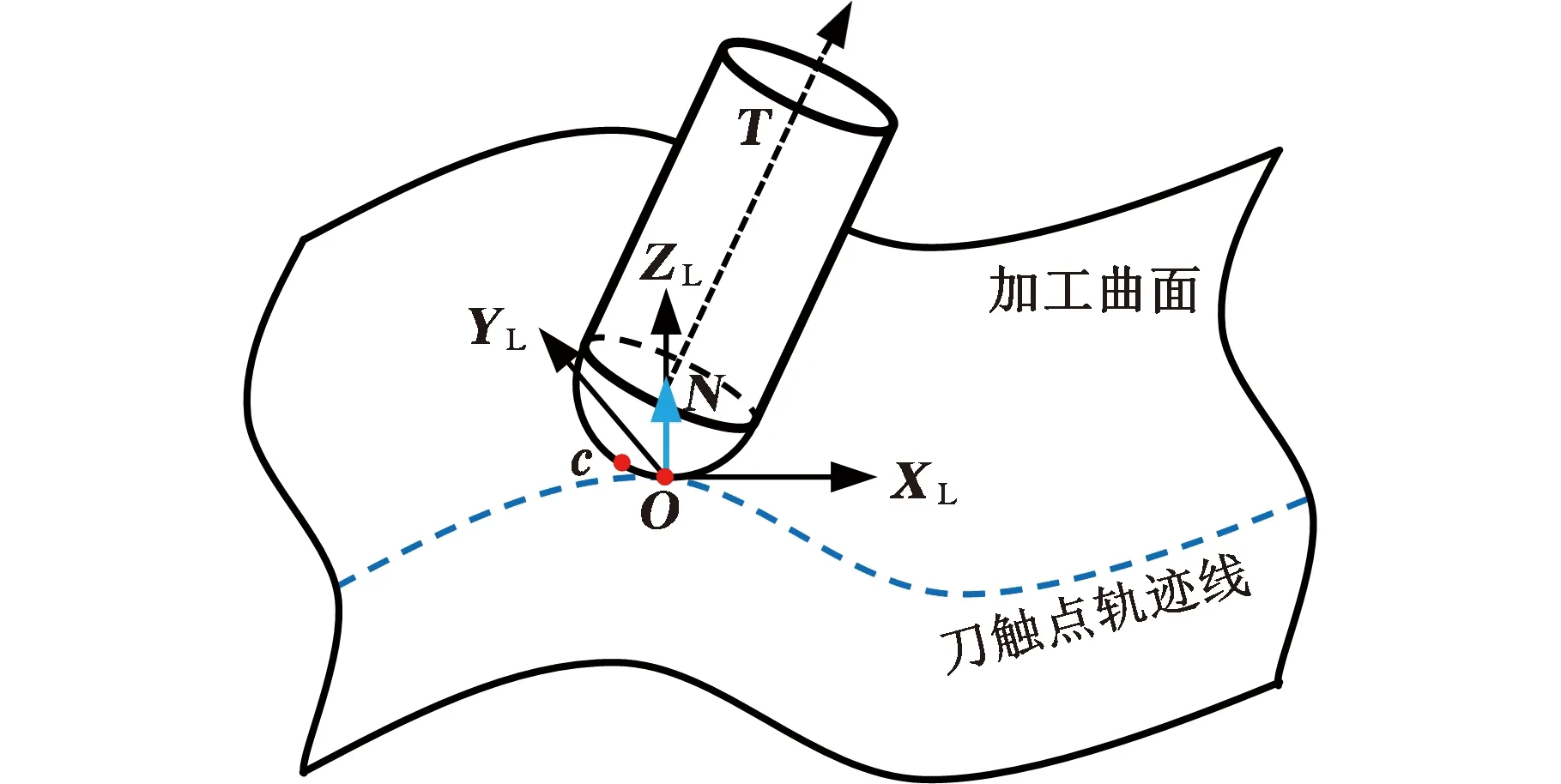
图1 球头铣刀刀位示意图
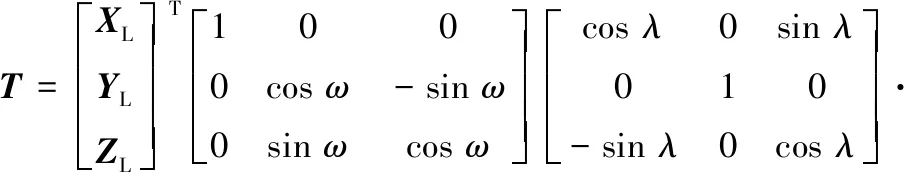
(1)
刀触点O和刀尖点c之间的关系为c=O-rT+rN,其中r表示球头铣刀半径。
1.2 机床旋转轴角度位置与刀具前/侧倾角关系
刀轴矢量不仅可以使用前倾角和侧倾角(λ,ω)表示,还可以使用机床旋转轴角度位置表示。以AC型双转台五轴机床为例,令θA和θC分别表示机床旋转轴角度位置,根据五轴机床运动学模型,刀轴矢量可表示为T=(sinθCsinθA,cosθCsinθA,cosθA)T。于是,当已知AC型双转台机床旋转轴角度位置时,可使用下式计算对应的刀具前倾角和侧倾角:
(2)
需要注意,不同结构类型的五轴机床,其运动变换关系不同,根据机床旋转轴角度位置计算刀具前倾角和侧倾角的公式也会有所不同。
1.3 刀轴矢量可行域
为避免局部干涉,球头铣刀刀具半径r应小于加工曲面最小曲率半径ρmin。针对加工路径的每一个刀触点,分别在机床旋转轴行程范围、刀具前倾角和侧倾角指定范围内采样,计算对应的刀轴矢量,然后采用基于距离的方法判断刀具、刀柄和工件是否发生碰撞干涉[9],具体步骤为:将所有需要进行碰撞干涉检查的曲面离散成点云,刀具、刀柄与工件的碰撞干涉检查转换为计算这些点云与刀具轴线的相对距离。为了缩短碰撞干涉检查时间,使用文献[15]的方法获取点云中与指定点的欧氏距离在指定半径范围内的点集,定位点云中可能与刀具和刀柄发生碰撞干涉的点集,减少后续运算负荷。需要注意的是,刀具前倾角为负的刀轴矢量需要从可行域中剔除,刀轴矢量可行域的刀具姿态使用机床旋转轴角度位置表示。
2 复杂曲面光顺刀轴矢量生成方法
采用等参数线法规划刀触点轨迹,然后利用等参数法将刀触点轨迹离散成许多刀触点,得到整个加工路径的刀触点集合。提出的基于关键刀轴矢量插值的刀轴矢量优化方法流程如图2所示,具体步骤如下:根据关键刀位的初始个数,在刀触点轨迹的参数域内等间隔采样,确定关键刀位的刀触点位置,然后确定每个初始关键刀位的刀轴矢量可行域;遍历首个关键刀位所有的可行刀轴矢量,针对其中第i个可行刀轴矢量,基于贪心策略从其他关键刀位的刀轴矢量可行域中选择刀轴矢量,这些关键刀轴矢量序列记为Si;线性插值关键刀轴矢量序列Si中的机床旋转轴角度位置,获得刀具路径所有刀触点处的刀轴矢量,如果这些刀轴矢量均未发生碰撞干涉,则将关键刀轴矢量序列Si放进集合H;如果集合H为空集合,则增加关键刀位个数,重复上述步骤,否则,通过刀尖点运动轨迹和机床旋转轴运动轨迹的一阶、二阶、三阶导数平方加权和(光顺评价指标),从集合H中选出最优的关键刀轴矢量序列,并计算刀具路径所有刀触点处的刀轴矢量。下面详细介绍各步骤。
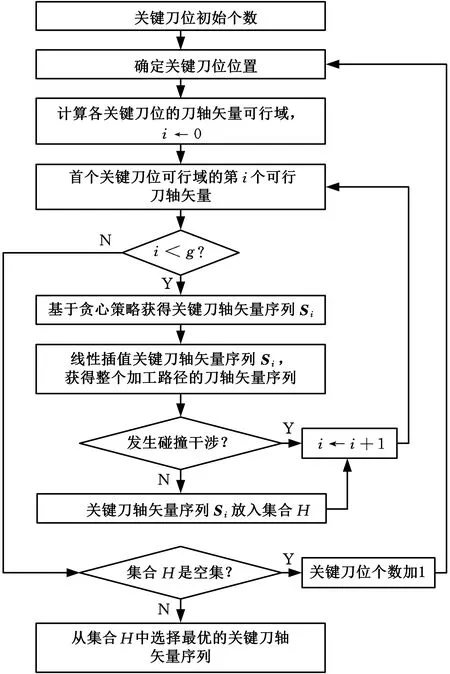
注:g是首个关键刀位的可行刀轴矢量个数。
2.1 刀具路径光顺评价指标
光顺的刀具路径包括刀尖点运动轨迹和旋转轴运动轨迹两者的光顺。类似于曲线的光顺评价指标,采用刀尖点运动轨迹和机床旋转轴运动轨迹的一阶、二阶、三阶导数平方和作为刀具路径光顺评价指标。使用B样条曲线插值加工路径的刀位数据获得刀尖点运动轨迹和机床旋转轴运动轨迹。令F′pt、F″pt和F‴pt分别表示刀尖点运动轨迹的一阶、二阶和三阶导数平方和,F′4、F″4、F‴4、F′5、F″5、F‴5分别表示机床旋转轴运动轨迹的一阶、二阶和三阶导数平方和,它们的表达式分别为
(3)
其中,P(u)表示刀具路径的刀尖点运动轨迹,C4(u)和C5(u)分别为机床旋转轴运动轨迹,[up,ul]是刀尖点运动轨迹和机床旋转轴运动轨迹的定义域[9]。式(3)各指标的矩阵表达式如下:
(4)
其中d4∈Rl、d5∈Rl是机床旋转轴运动轨迹的控制点,dpt∈R3l是刀尖点运动轨迹的控制点,l表示刀具路径的控制点个数,Rl和R3l分别表示l维的实数集合和3l维的实数集合。H1、H2、H3表示刚度矩阵,其计算方式如下:
(5)
其中0≤i,j≤l-1,p表示B样条曲线次数,Bi,p(u)是B样条曲线的基函数。
2.2 关键刀位的刀轴矢量可行域
2.3 关键刀轴矢量序列线性插值
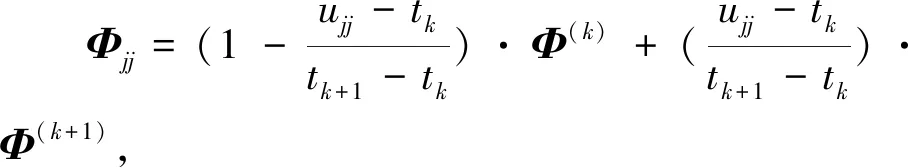
2.4 基于贪心策略的关键刀轴矢量序列选择
关键刀轴矢量序列会直接影响整个加工路径各刀触点处刀轴矢量,如何合理选择各关键刀位处刀轴矢量是难点。首个关键刀位处有多个可行刀轴矢量,但现有方法仅从首个关键刀位的刀轴矢量可行域内选择一个刀轴矢量作为关键刀轴矢量。为此,提出了基于贪心策略确定关键刀轴矢量序列的方法。
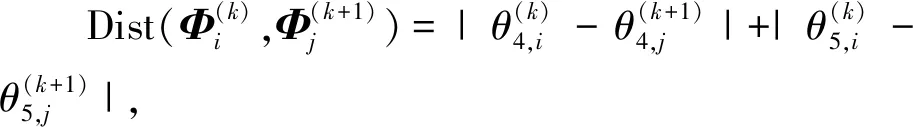
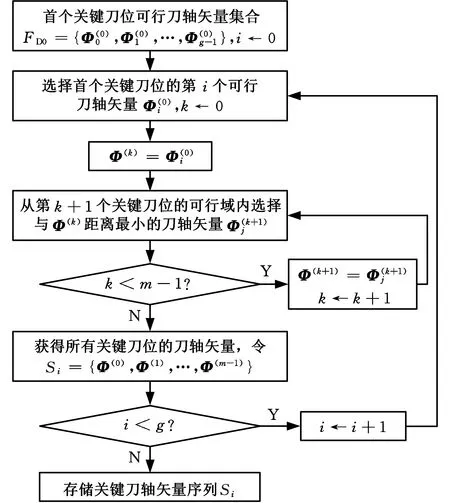
图3 贪心策略流程图
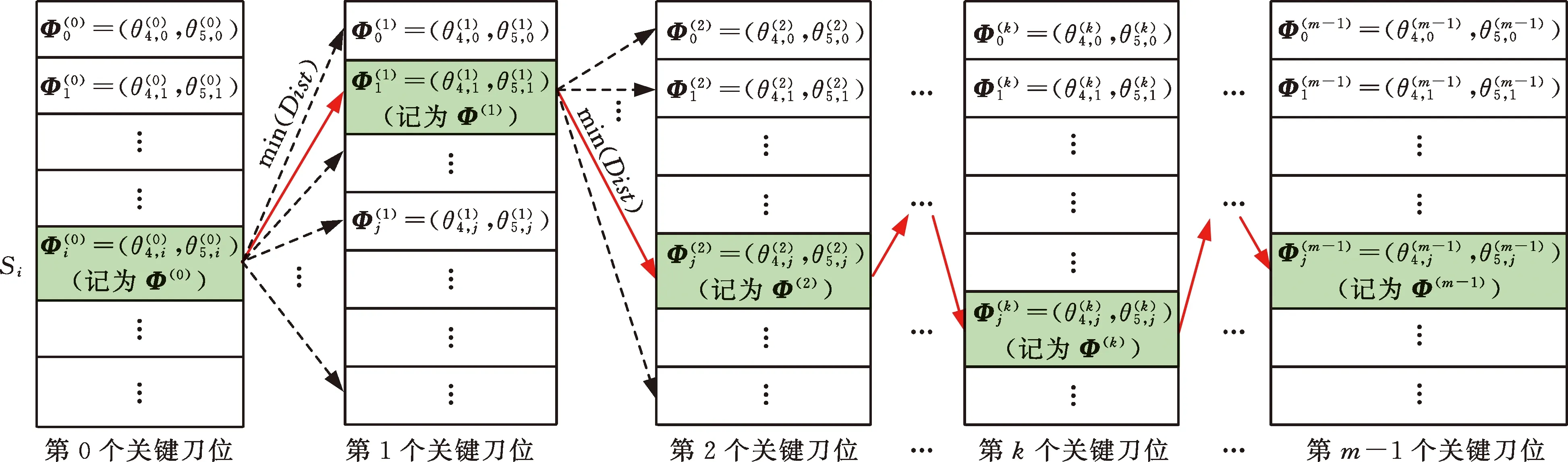
图4 基于贪心策略的关键刀轴矢量序列选择示意图
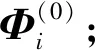
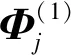
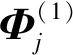
(4)线性插值关键刀轴矢量序列Si,获得整个加工路径各刀触点处刀轴矢量,并进行碰撞干涉检查;如果未发生碰撞干涉,则把关键刀轴矢量序列Si放入集合H;
(5)重复上述步骤,直至遍历完首个关键刀位所有可行刀轴矢量,最后获得关键刀轴矢量序列集合H。
2.5 最优关键刀轴矢量序列确定
以贪心策略获得关键刀轴矢量序列集合H后,针对集合H的每一个关键刀轴矢量序列Si,通过线性插值方法得到整个刀具路径的刀轴矢量序列,计算对应的刀尖点集合{ci|i=0,1,…,n-1}。使用B样条曲线插值这些刀位数据(具体计算方法见文献[9]),并根据式(3)计算刀具路径光顺评价指标。令{F′pt,j}、{F″pt,j}、{F‴pt,j}、{F′4,j}、{F″4,j}、 {F‴4,j}、{F′5,j}、{F″5,j}、{F‴5,j}分别表示集合H中各关键刀轴矢量序列Sj对应的光顺性指标集合,根据评价指标:
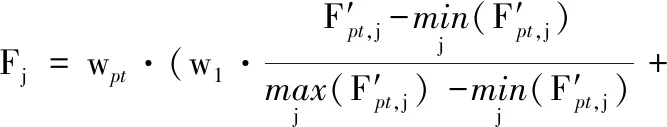
(6)
从集合H中选取最优的关键刀轴矢量序列Sbest,其中w1、w2、w3分别是刀尖点运动轨迹和机床旋转轴运动轨迹一阶、二阶、三阶导数平方和的权重,wpt、w4、w5分别表示刀尖点运动轨迹、机床旋转轴运动轨迹对应的光顺性权重。最后线性插值关键刀轴矢量序列Sbest,获得整个加工路径光顺的刀轴矢量序列以及对应的刀尖点运动轨迹。
3 仿真算例与加工试验
为验证所提球头铣刀五轴加工光顺刀具姿态生成方法的有效性,本节将借助Siemens NX提供的API函数生成叶片曲面的加工路径。使用的五轴机床为双转台AC型机床,其旋转轴行程范围分别为-10°≤θ4≤110°,0°≤θ5≤360°,刀具前倾角和侧倾角的范围分别为0°≤λ≤90°,-180°≤ω≤180°。
3.1 叶盘叶片曲面加工
针对图5所示叶片曲面和叶盘模型(叶展方向长度约40 mm),使用等参数线法规划刀触点轨迹,相邻刀触点轨迹的步距由指定的最大残余高度决定,本算例最大残余高度设为0.002 mm。精加工使用的球头铣刀参数如下:直径8 mm,刃长16 mm,4齿。

(a)叶片曲面 (b)碰撞检测曲面
使用所提方法生成叶片曲面精加工路径的参数如下:刀触点轨迹的刀触点个数n=120,关键刀位初始个数m=10。可依据刀触点轨迹曲线的弧长来选择关键刀位初始个数。计算刀轴矢量可行域时,刀具前倾角和侧倾角采样间隔均设为4°,机床旋转轴角度位置采样间隔设为2°,图5b中橙色曲面是计算刀轴矢量可行域时需要进行碰撞干涉检查的曲面。式(6)中各权重分别为w1=0.6,w2=0.3,w3=0.1,w4=0.45,w5=0.35,wpt=0.2。
在计算机上运行编写的程序计算叶片曲面精加工路径,最终曲面有167条加工路径。这些加工路径对应的机床旋转轴运动轨迹如图6所示。可以看到,曲面的加工路径对应的机床旋转轴运动平稳。
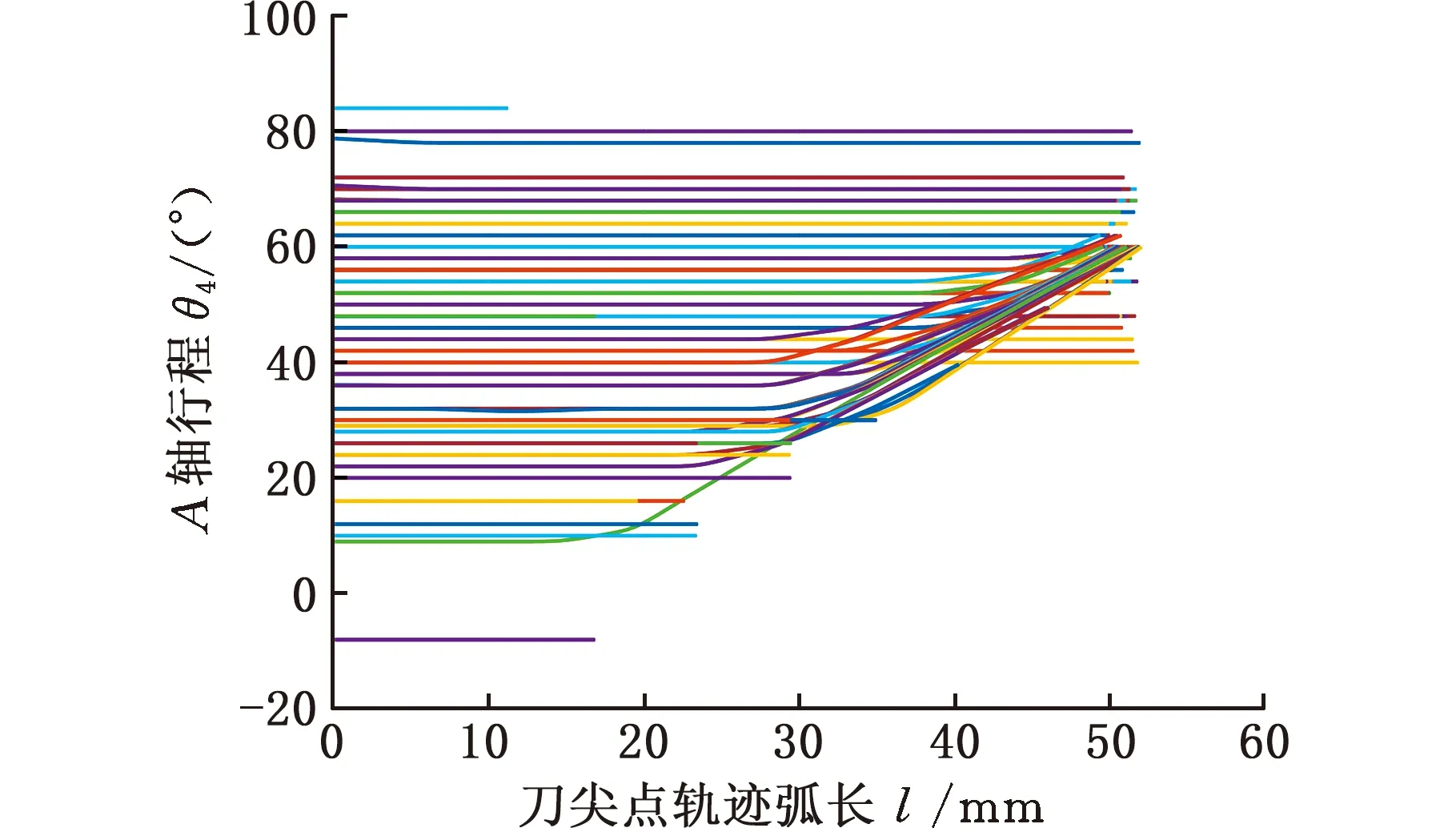
(a)A轴运动轨迹
使用生成的刀具路径在五轴机床上进行切削加工实验,工件材料为6061铝合金。在精加工时,主轴转速设为20 000 r/min,进给速度为1200 mm/min,精加工余量为0.2 mm,顺铣加工。刀具悬伸长度约39 mm。叶片曲面加工结果如图7所示。刀具悬伸长、叶片弱刚性以及加工参数选择不恰当将导致加工过程发生振动,叶片曲面顶部的加工表面留有刀具振纹。所提方法在生成五轴加工刀具姿态时只考虑了五轴加工的几何学和运动学问题,未考虑五轴加工动力学问题。如何合理选择叶片曲面五轴铣削加工的加工参数是研究难点。参考文献[16]的方法,通过加工参数优化减小加工过程的振动,改善叶片曲面表面质量。

图7 叶片曲面加工结果
3.2 涡轮叶片曲面加工
使用所提方法生成图8所示涡轮叶片曲面的刀具加工路径(叶展方向长度约50 mm)。使用等参数线法规划刀触点轨迹,最大残余高度设为0.001mm。相邻叶片的距离在靠近轮毂处只有5mm左右,因此,精加工时使用的球头铣刀参数如下:直径4 mm,刃长6 mm,2齿。

(a)叶片曲面A (b)叶片曲面B
该涡轮叶片长度大,为了减少加工过程的振动,把叶片曲面按照等参数线分成4个区域加工(如图8d所示),每个区域使用不同的刀具悬伸长度,提高加工系统的刚度。图8c中橙色曲面是计算刀轴矢量可行域时需要进行碰撞干涉检查的曲面。计算刀轴矢量可行域时,刀具前倾角和侧倾角采样间隔均设为2°,机床旋转轴角度位置采样间隔设为2°。每条刀触点轨迹的刀触点个数n=50,关键刀位初始个数m=6。
使用所提方法生成叶片曲面4个区域的精加工路径,各权重分别为:w1=0.6,w2=0.3,w3=0.1,w4=0.45,w5=0.35,wpt=0.2,各区域精加工路径对应的机床旋转轴运动轨迹如图9~图12所示,可见机床旋转轴角度位置变化平稳。使用Vericut软件进行切削加工几何仿真,结果如图13所示。加工仿真过程中未发生刀具-刀柄-工件碰撞干涉现象,验证了所提方法的有效性。
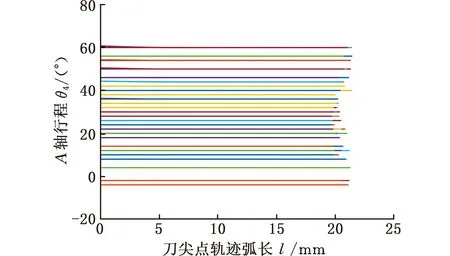
(a)A轴运动轨迹
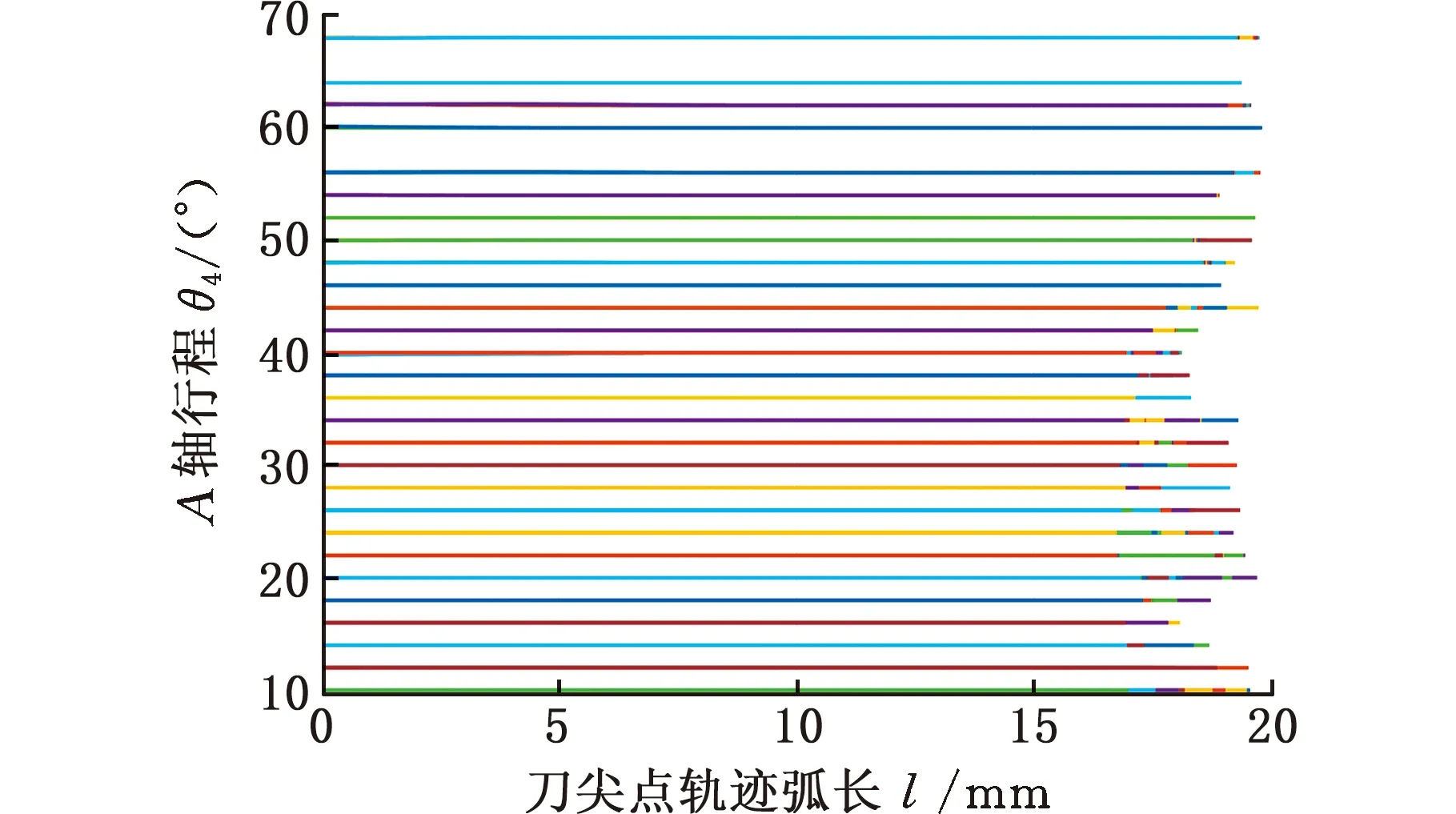
(a)A轴运动轨迹
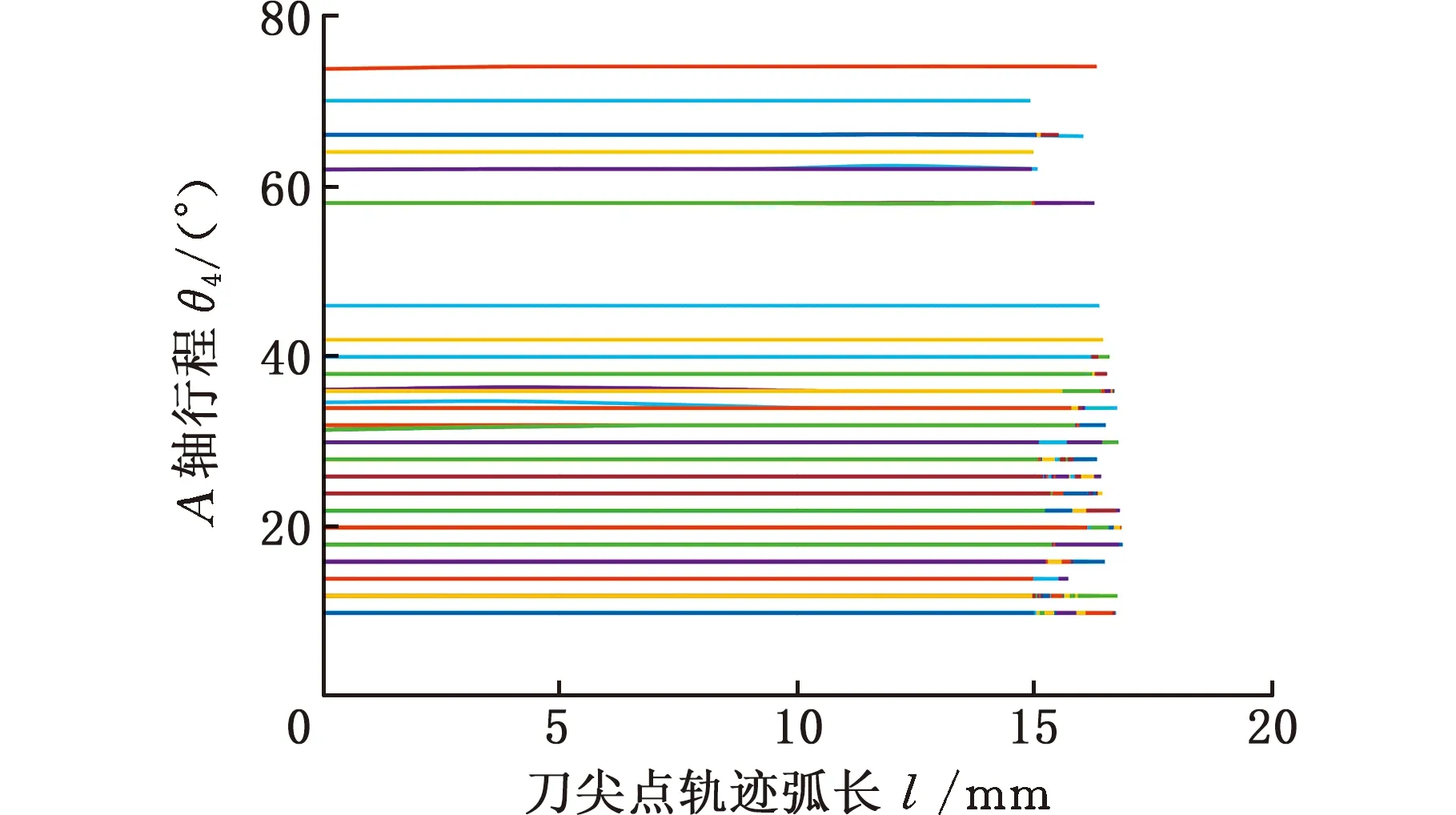
(a)A轴运动轨迹
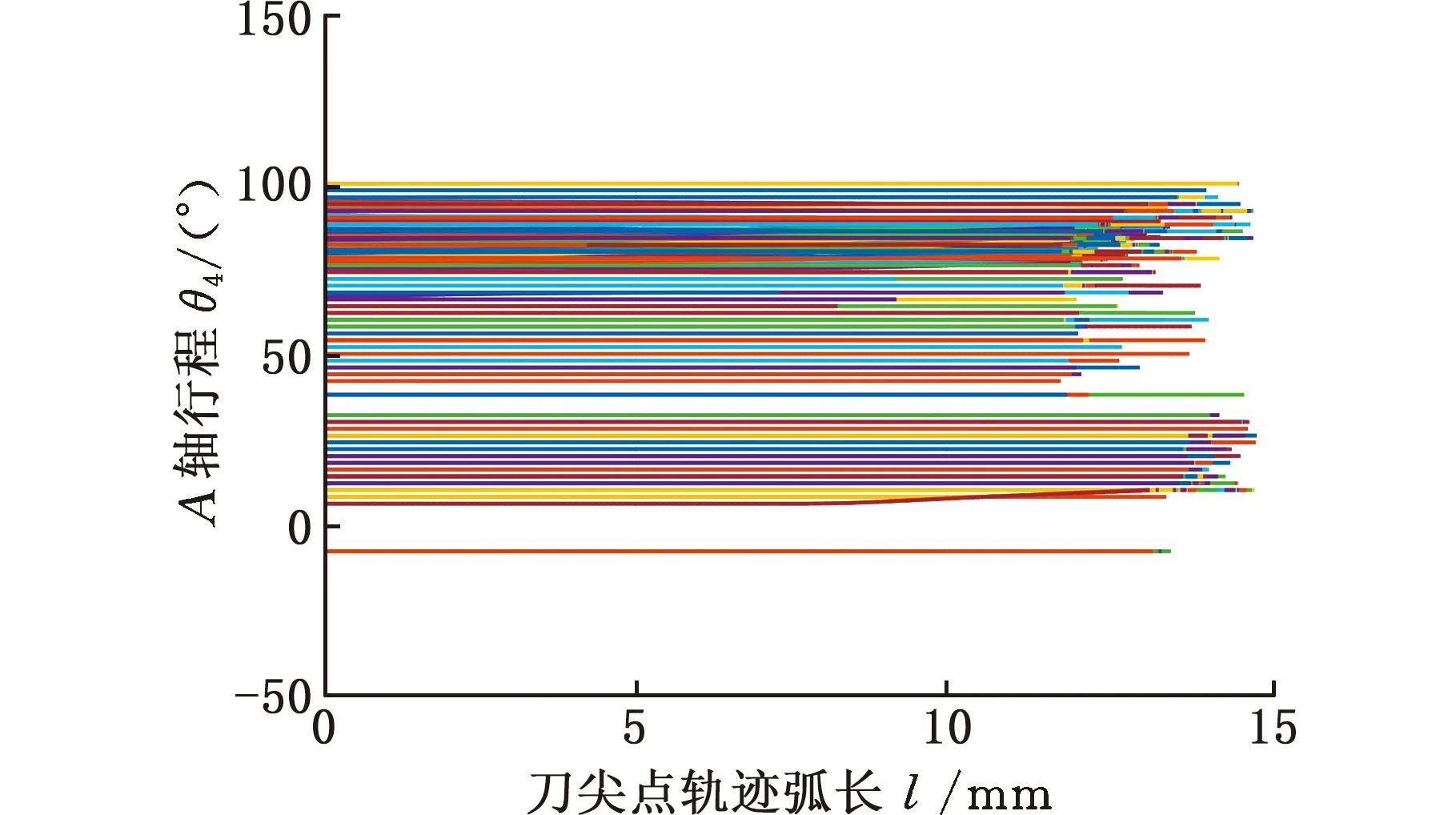
(a)A轴运动轨迹

(a)叶片曲面A (b)叶片曲面B
4 结论
(1)基于关键刀轴矢量插值的刀轴矢量优化方法避免了计算整个加工路径各刀触点处刀轴矢量可行域,可缩短光顺刀轴矢量生成时间。针对目前基于关键刀轴矢量插值的光顺刀轴矢量生成方法存在的不足,提出了关键刀轴矢量序列整体优化方法。
(2)提出了基于关键刀轴矢量插值的球头铣刀加工叶片复杂曲面的光顺刀具姿态生成方法,该方法使加工过程机床旋转轴运动平稳。
(3)通过仿真试验与实际加工测试验证了所提方法的有效性。
