自适应卡尔曼滤波与PSO-GA-BP算法的机器人误差补偿
2023-11-15李光保周愿愿
李光保 高 栋 路 勇 平 昊 周愿愿
1.哈尔滨工业大学机电工程学院,哈尔滨,1500002.上海航天精密机械研究所,上海,201600
0 引言
某型号发射筒(箱)口框位置的切割开孔,传统模式是采用人工划线、手持切割锯进行切割,存在质量稳定性差、效率低、劳动强度大等问题。为了满足常态化高强密度发射形式下导弹快速、批量研制的需求,考虑到激光切割(以中薄板为主)的切割速度快、加工精度高、切缝狭窄等一系列优点[1-2]以及待切割对象形状各异的特点,采用七轴机器人夹持激光切割头的方式对发射筒(箱)进行切割,配合工件装夹平台,发射筒(箱)可完成360°回转,从而将可切割范围覆盖整个发射筒(箱)。但是工业机器人在安装和加工过程中存在几何误差[3-5],另外,其末端在负载和各关节自重的影响下结构发生受力变形,相对应的工业机器人位置也发生偏差,而且运动过程中控制指令发出的脉冲信号容易受到环境干扰,多种因素共同作用使得工业机器人的轨迹精度和定位精度无法得到保证[6-7]。
目前工业机器人误差补偿主要通过激光跟踪仪或多传感器融合采集工业机器人位姿信息作为机器人真实位姿信息。由于一般未考虑测量不确定度问题[8],实际提出的补偿量误差较大。本文针对七轴激光切割机器人,基于Sage-Husa自适应卡尔曼滤波方法建立理想机器人模型[9-10],求解真实的七轴机器人位姿参数;同时采用粒子群优化-遗传算法-BP神经网络(PSO-GA-BP)联合算法建立七轴机器人关节补偿预测模型,并与遗传算法-BP神经网络(GA-BP)算法及粒子群优化-BP神经网络(PSO-BP)算法的预测结果进行对比,最后通过Workvisual 5.0软件对工业机器人各坐标点误差补偿,然后进行加工。
1 七轴激光切割机器人工作原理
七轴激光切割机器人主要由库卡机器人、外部第七轴、发射筒(箱)主轴箱、激光单元、控制系统、水冷机、设备操作台、机器人导轨平台、激光安全防护房等部分组成,如图1所示。机器人选择库卡机器人KR50 R2500结合Y向外部轴电机构成七轴机器人,另外在七轴机器人的末端安装激光切割头,搭建相应的七轴KRC4高性能机器人控制器,附带相应的手持编程器。控制器选配Beckhoff EK1100 EtherCAT通信耦合器与主控制器内部通信,通过EL6631 Profinet通信端子模块进行Profinet通信网路组态与PLC通信,确保控制系统数据信息的实时性能。通过对主控制器进行编程,将激光单元、主轴箱电机、水冷机、辅气系统的运行与机器人本体及第七轴动作结合,合理设计逻辑时序,实现发射筒(箱)激光切割工艺流程。

图1 发射筒七轴激光切割机器人
2 七轴机器人模型的建立
为实现对七轴机器人的误差补偿,运用D-H建模方法建立七轴机器人模型,通过正逆运动学数值算法对建立的七轴机器人模型进行验证,证明模型的正确性,为误差补偿预测模型的建立提供机器人理论位姿数据。
2.1 库卡七轴机器人
发射筒(箱)激光切割采用的机器人结构形式如图2所示,由六根可活动的、相互连接到一起的轴组成,同时在六轴机器人底座位置增加Y轴方向滑动的第七轴,用于机器人Y轴方向的移动。因此,采用的七轴激光切割机器人各连杆的空间坐标系如图2所示。
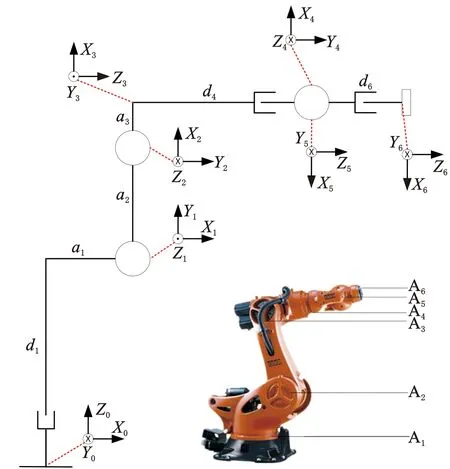
图2 库卡KR50 R2500结构形式
2.2 D-H建模
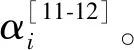
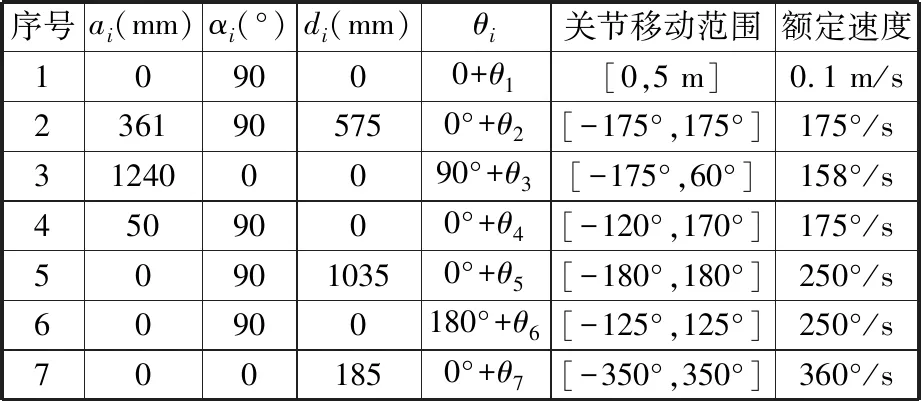
表1 D-H参数
根据表1中的机器人D-H参数,运用机器人工具箱中的Link函数分别建立6个旋转杆件模型和1个移动杆件模型,采用qlim函数定义A1~A7的关节驱动范围,使用SerialLink类函数将Link函数建立的连杆连成一个整体,生成一个串联机械臂模型。运行程序后七轴机器人模型如图3所示。此时,θ1=0.897 43 m,θ2=-1.4694 rad,θ3=-1.8459 rad,θ4=-3.1416 rad,θ5=0.241 79 rad,θ6=-0.436 66 rad,θ7=1.7907 rad,x=1.651 m,y=0.275 m,z=0。
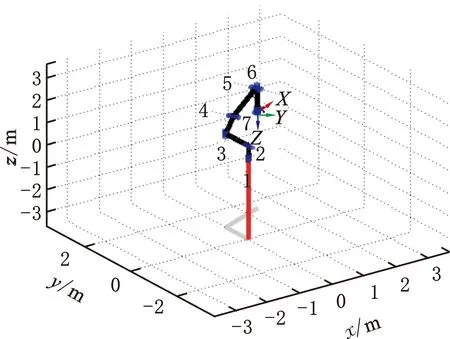
图3 七轴库卡机器人模型
2.3 正逆运动学验证
根据D-H算法确定的参数,用旋转和位移来表示相邻关节坐标系间齐次变换关系[13]:
(1)
式中,(nx,ny,nz)T、(ox,oy,oz)T、(ax,ay,az)T均为激光切割器在基坐标系下的旋转姿态参数;(px,py,pz)T为激光切割器在基坐标系下的位置参数。
七轴机器人末端激光切割器在机器人基坐标系下的位姿可定义为(x,y,z,α,β,γ)T,其中:
(3)
(4)
(5)
式中,(x,y,z)为激光切割器的位置坐标;(α,β,γ)为激光切割器坐标系与基座坐标系三坐标轴的夹角。
随机选取七轴机器人运行范围内的各关节参数进行验证,如图4所示。此时,θ1=1.092 m,θ2=0.132 93 rad,θ3=0.181 37 rad,θ4=-0.156 43 rad,θ5=0.1885 rad,θ6=-3.1166 rad,θ7=-1.8221 rad,x=1.642 m,y=1.312 m,z=0.106 m。
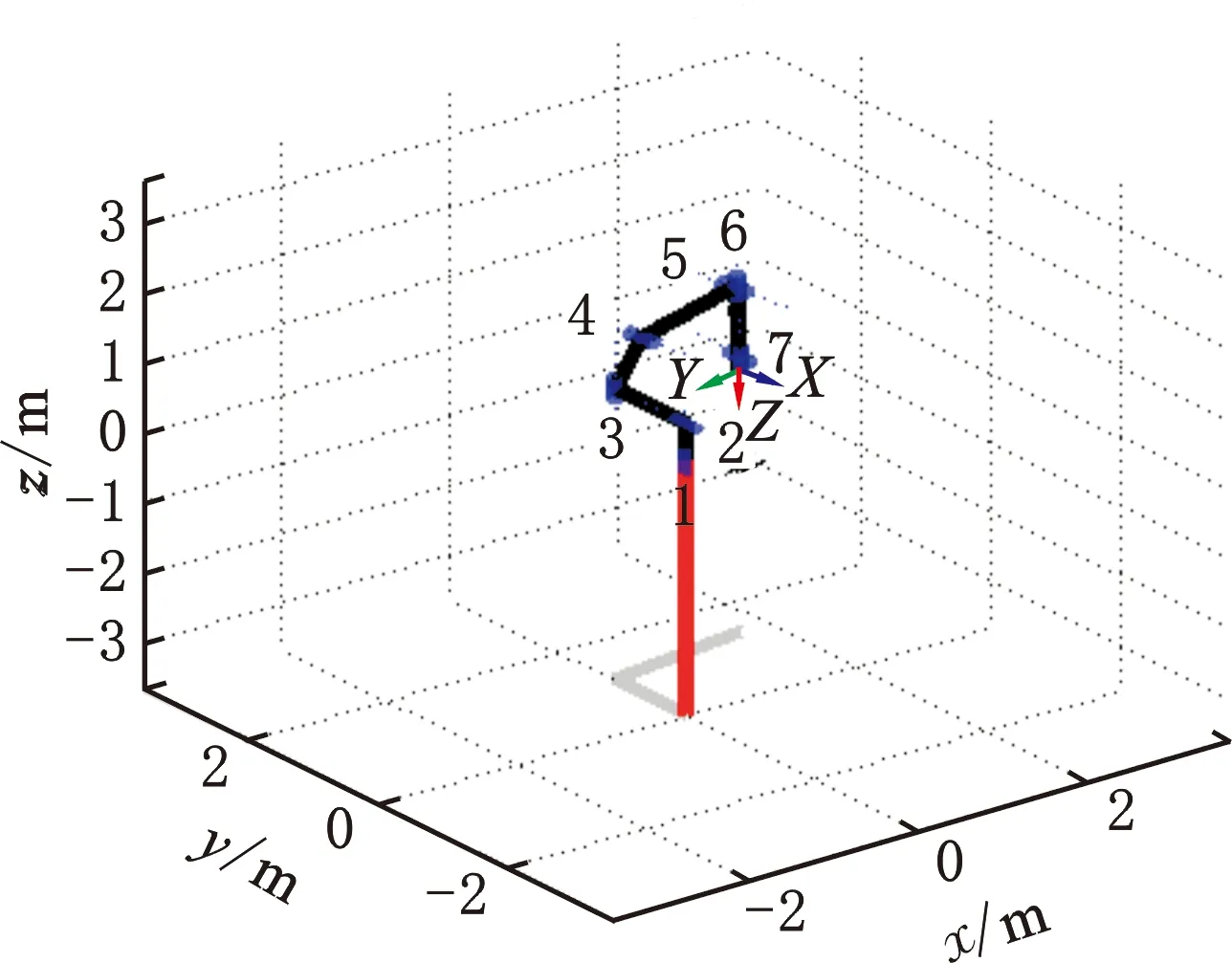
图4 七轴机器人正运动学求解
根据表2随机产生的七轴关节角度值,运用正运动学数值法建立机器人模型,求得的位姿误差最大值为0.0003 m,验证了本文中建立的七轴机器人模型具有较高的正运动学计算精度。
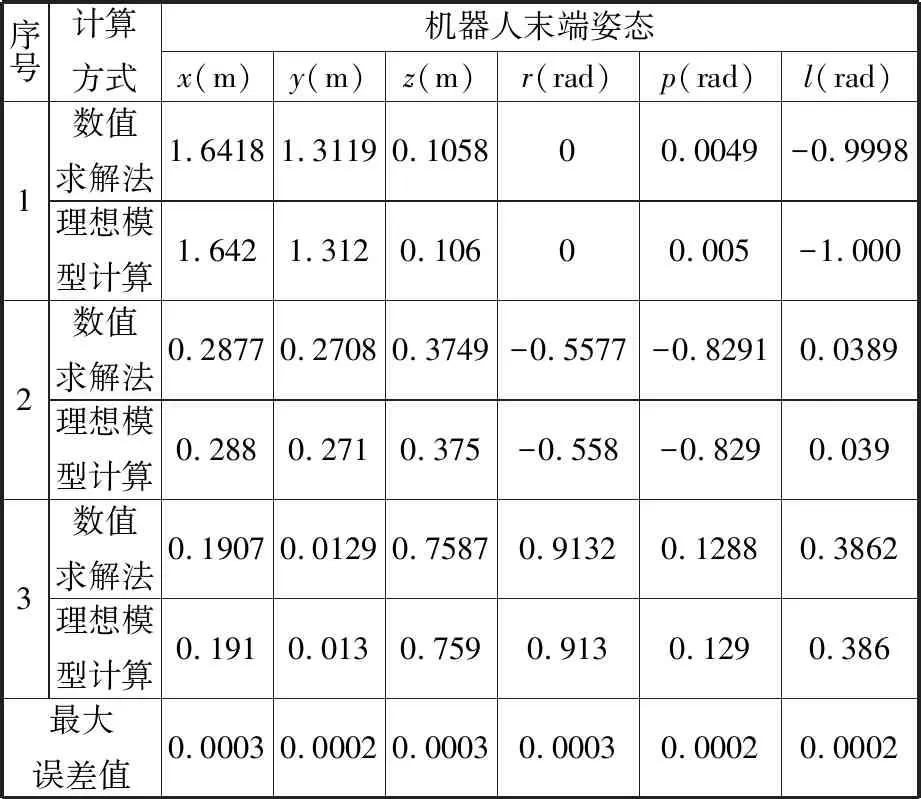
表2 机器人正运动学计算末端姿态值
运用代数求解法完成逆运动学求解,逐个分离变量求解,得到各关节数值[14],即用矩阵逐次左乘简化方程,可得如下方程:
(6)
(7)
计算结果如表3所示。
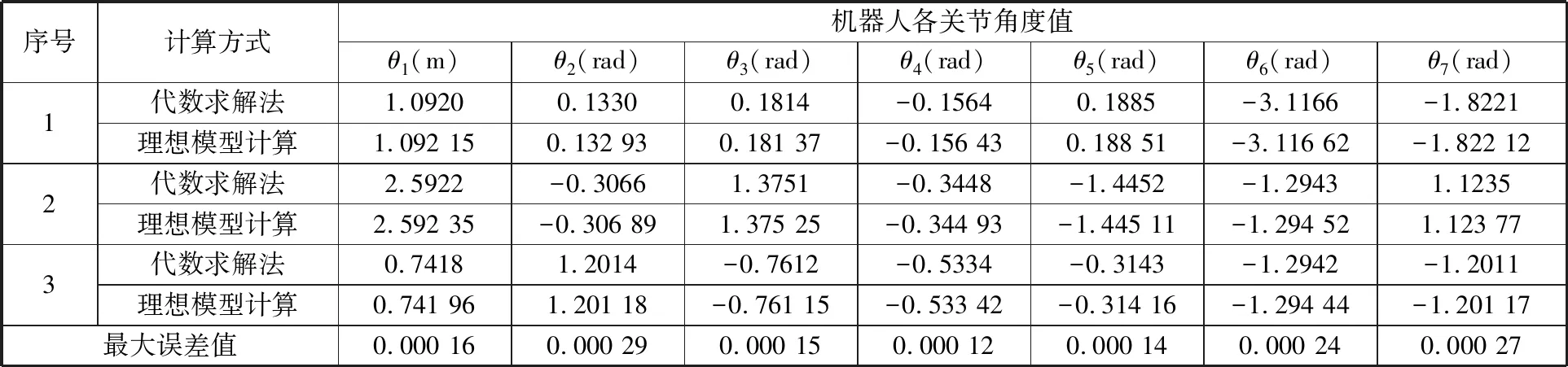
表3 逆运动学求解的各关节角度值
根据随机选择的机器人位姿运用代数求解法和运用机器人工具箱建立机器人模型,求得各关节角度值误差最大值为0.0003 rad,验证了本文中建立的七轴机器人模型具有较高的逆运动学计算精度。
由上述计算结果可证明建立的七轴库卡机器人仿真模型具有较高的数据可信度,可作为机器人位姿理论数据进行处理。
3 Sage-Husa自适应卡尔曼滤波
3.1 卡尔曼滤波
卡尔曼滤波是根据上一时刻的最优估计值和此时刻的测量值来进行连续的加权计算,对测量环境中存在的各种混合噪声干扰进行滤除[15],从而得到当前时刻的最优估计值。结合本文研究的问题,以某一时刻七轴机器人理论模型显示的位姿为卡尔曼滤波算法中的预测值,激光跟踪仪测量的七轴机器人位姿为卡尔曼滤波算法中的测量值,建立的状态方程和测量方程如下:
状态方程
Xk+1=φkXk+Bkuk+ωk
(8)
式中,Xk+1为k+1时刻6维的系统状态变量,包括(x,y,z,r,p,l)机器人位姿参数;φk、Bk为系统参数;uk为机器人控制系统的输入量;ωk为机器人控制系统噪声偏差。
观测方程
Yk+1=Ck+1Xk+1+γk+1
(9)
式中,Yk+1为k+1时刻的机器人位姿测量值;Ck+1为k+1时刻的测量系统参数;γk+1为激光跟踪仪测量噪声偏差。
卡尔曼滤波随着时间的更新而不停地更新预测值和校正值,其中:
(10)
(11)
(12)
(13)
(14)
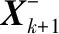
式(10)、式(11)、式(12)为预测方程,式(13)、式(14)为校正方程。式(10)~式(14)为卡尔曼滤波算法的迭代公式,根据分析发现卡尔曼滤波主要依赖系统噪声和测量噪声模型的准确性。
3.2 基于Sage -Husa的自适应卡尔曼滤波器
针对以上情况,本文采用基于Sage-Husa的自适应卡尔曼滤波来解决系统噪声和测量噪声模型不准确的问题,实时更新估计突变噪声的均值、协方差,从而对模型参数和噪声特性进行实时修正,以减小与实际情况的误差[16]。基于Sage-Husa的自适应卡尔曼滤波算法是在卡尔曼滤波每次迭代的同时对噪声模型进行一次更新计算,使得系统噪声和测量噪声均值、协方差的值保持在最优估计值的状态,系统噪声和测量噪声均值、协方差更新如下所示:
(15)
(16)
(17)
dk=(1-b)/(1-bk+1)
(18)
3.3 结果对比
将采集的数据分别使用卡尔曼滤波与基于Sage-Husa的自适应卡尔曼滤波进行滤波降噪。根据工程实践的经验法,采集系统中卡尔曼滤波器的系统噪声协方差设为0.001,测量噪声协方差R设为0.0025,本文采用七轴库卡机器人中Y轴坐标信息进行实验,卡尔曼滤波与基于Sage-Husa的自适应卡尔曼滤波的数据处理结果如图5所示,误差如图6所示。
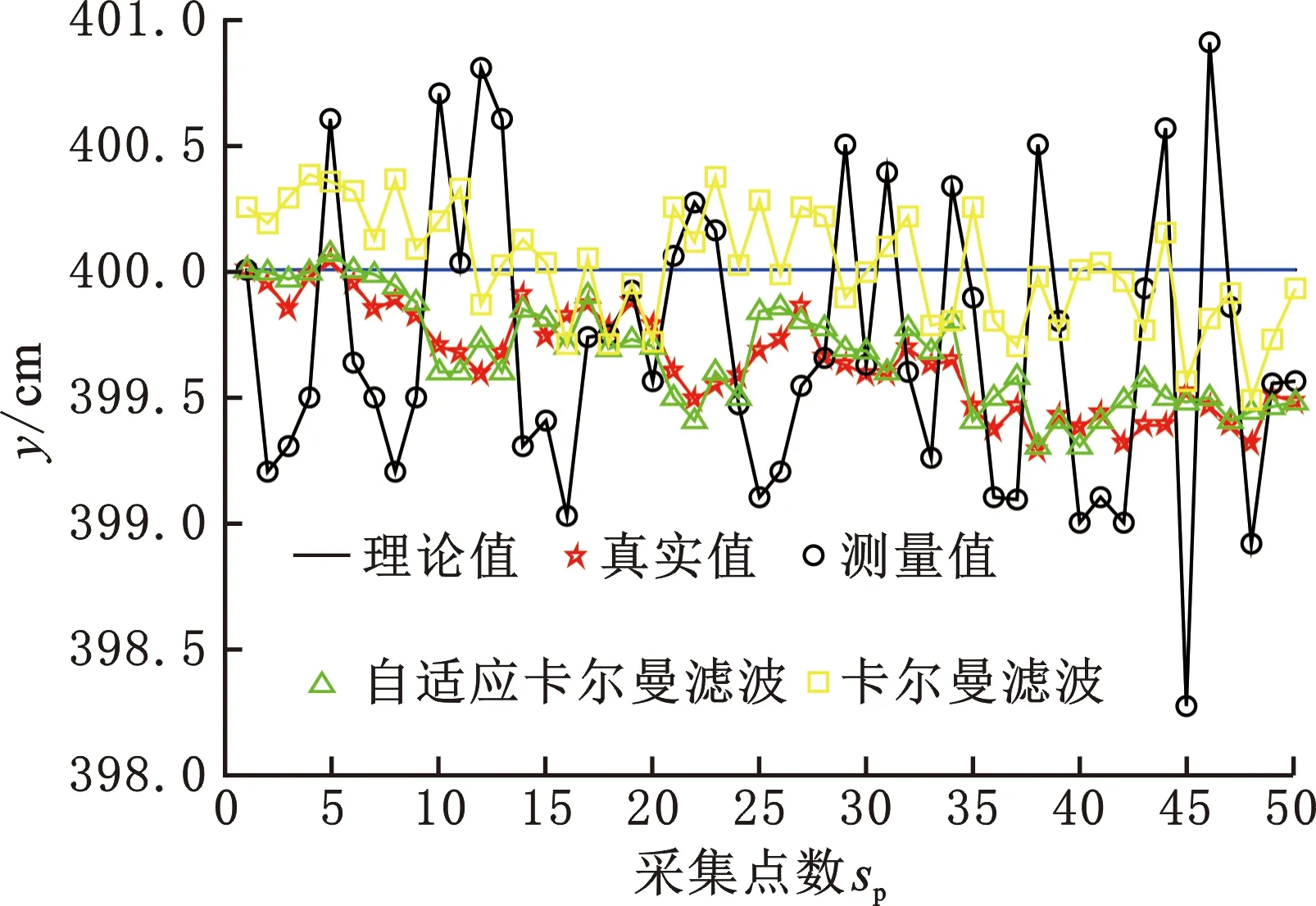
图5 数据分析
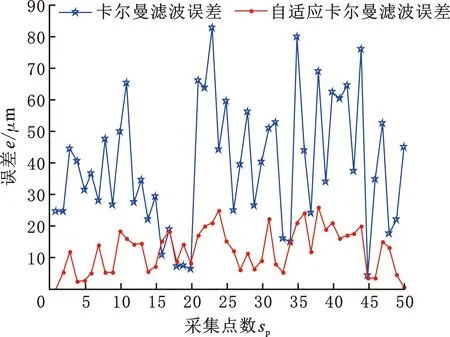
图6 误差分析
4 基于PSO-GA-BP的神经网络误差模型的建立
针对传统机器人误差模型预测方法精度低、需求量大的问题,提出误差反传BP神经网络误差预测模型[17],并利用遗传算法GA模型优化BP神经网络结构模型,再运用粒子群算法PSO优化GA-BP神经网络模型的权值和阈值,从而提高模型的收敛速度以及预测精度。PSO-GA-BP的神经网络误差模型算法流程如图7所示。数据集分为训练数据集和测试数据集。
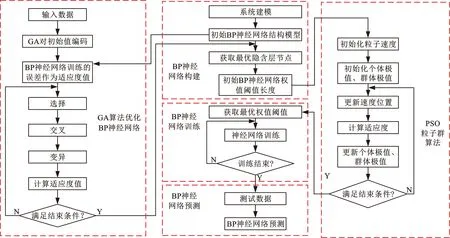
图7 PSO-GA-BP神经网络算法流程
4.1 BP神经网络模型
BP神经网络是一种按误差反向传播算法训练的前向神经网络,一般由输入层、隐含层和输出层组成[18],其数学模型如下所示:
Iout1=f1(w1Iin+b1)
(19)
Iout2=f2(w2Iout1+b2)
(20)
(21)
式中,Iin、f1、w1、Iout1和b1分别为神经网络输入层的输入、隐含层的传递函数、输入层和隐含层之间的连接权值、隐含层的输出、输入层和隐含层之间的连接阈值;Iout2、f2、w2、和b2分别为输出层的输出、输出层的传递函数、隐含层与输出层的连接阈值、隐含层与输出层的连接阈值;h为隐含层节点数;m为输入层节点数;n为输出层节点数;ae为常数,ae∈[1,10]。
理论证明3层的神经网络能逼近任意的非线性映射关系,因此本文采用3层神经网络结构。
根据BP神经网络模型,首先选取七轴库卡机器人的理想位姿参数作为BP神经网络模型输入,包括坐标位置信息以及沿X、Y、Z方向的转动角度。理论位姿计算出的各轴关节角度值与经过Sage-Husa自适应滤波后的各轴关节角度值之差作为BP神经网络模型的输出。输入为6个参数,输出为7个参数,隐含层的节点数根据经验式(21)确定。
基于BP神经网络的七轴机器人误差预测模型如图8所示。
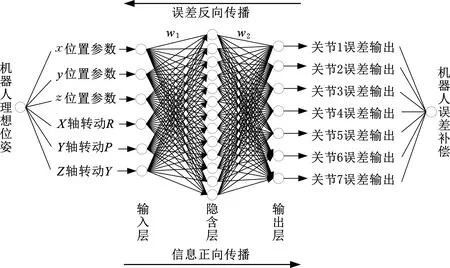
图8 BP神经网络误差预测模型
根据经验公式,隐含层的节点数h区间为[4,13]。选择的隐含层节点数越多,则非凸的目标函数越复杂,局部最小值点成倍增长,利用有限的数据集训练的BP神经网络模型性能较差,而且结构参数也会呈几何级增长;若训练数据较少,则容易出现过拟合现象。过少的隐含层节点又不能完整地反映输入和输出的函数关系。针对此类问题,本文运用GA算法求解最适用的隐含层节点数。
4.2 GA-BP算法选取最优隐含层节点数
对GA算法首先进行种群初始化,包括种群规模、迭代次数,设置各参数的取值范围。根据BP神经网络的初始网络结构,通过GA算法对BP神经网络进行优化,以BP神经网络模型预测值和实际值之间的误差平方和为适应度函数。
(1)选择操作。本文选用基于适应度比例的轮盘赌法选择策略,每个个体i的选择概率Pi为
式中,Fi为个体i的适应度值,由于适应度越小越好,所以在个体选择前对适应度值取倒数;ke为系数;N为种群个数。
(2)交叉操作。由于在本文中个体采用实数编码,所以交叉操作采用实数交叉法,第k个染色体ak和第i个染色体ai在j位的交叉操作如下:
akj=akj(1-be)+aijbe
aij=aij(1-be)+akjbe
式中,be为[0,1]之间的随机数。
(3)变异操作。本文采用单点变异方法,即选取第i个个体的第j个基因进行变异:
f(g)=r2(1-g/Gmax)2
式中,amax、amin为基因aij的上界和下界;r2为一个随机数;g为当前迭代次数;Gmax为最大进化次数;r为[0,1]之间的随机数。
适应度函数和适用隐含层节点数如图9、图10所示,根据仿真分析可知,隐含层节点数为10时均方差较小,故本文中的BP神经网络结构选取10为隐含层节点数。
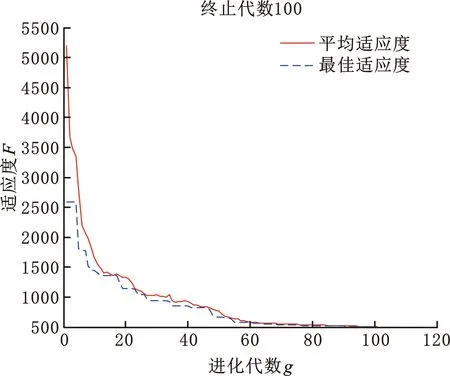
图9 适应度曲线
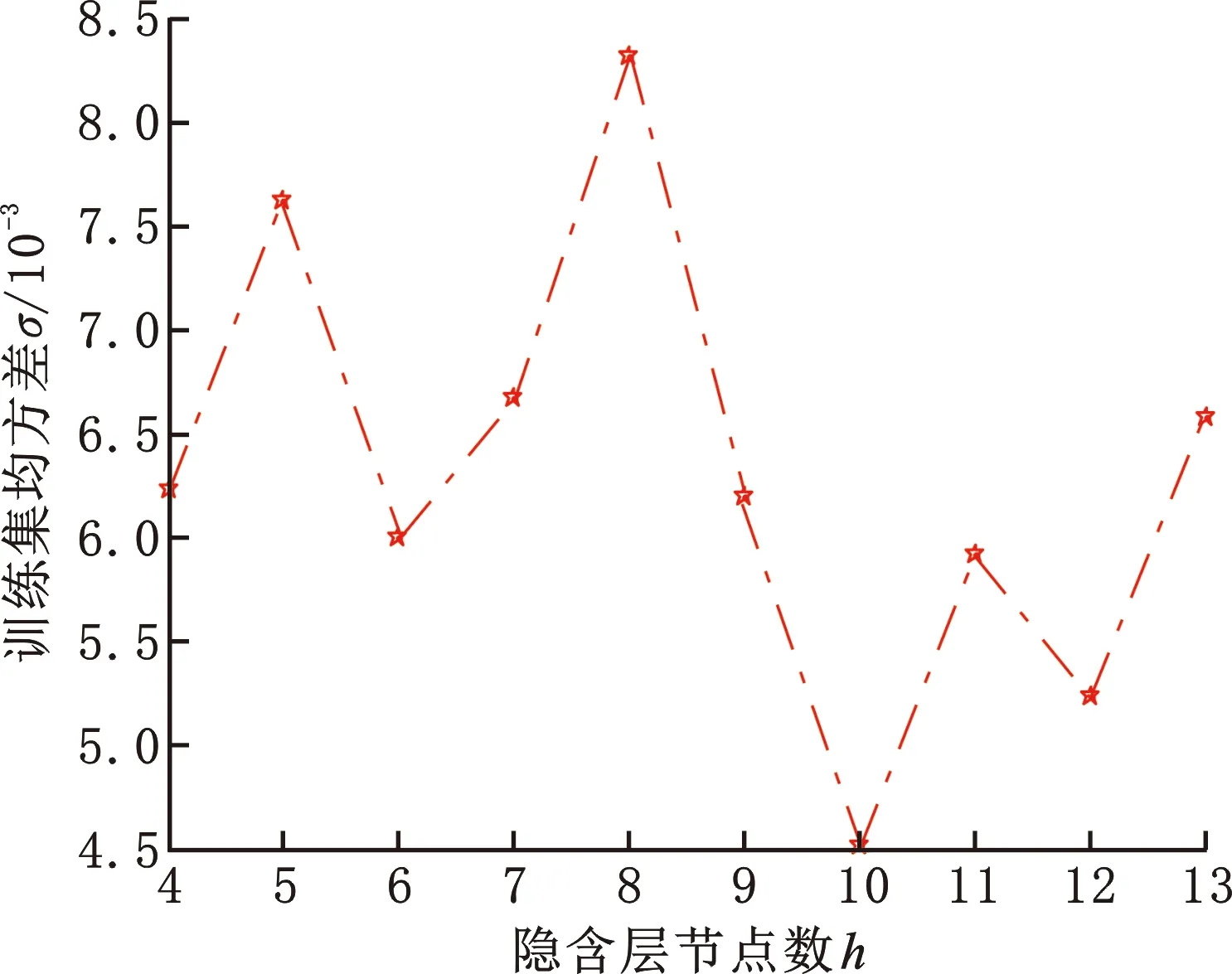
图10 隐含层节点数对应均方差
4.3 基于PSO-GA-BP算法的误差预测模型
运用PSO 算法对BP神经网络进行全局搜索,防止BP神经网络陷入局部最优[19],通过更新粒子速度和位置寻找全局最优粒子,对 BP 神经网络的权值和阈值进行优化,实现对七轴库卡机器人误差预测模型的构建。PSO算法参数设置为:惯性权重we,学习因子ce1、ce2,粒子最大速度和最大迭代次数。本文选用自适应调整的线性递减惯性权重,惯性权重的典型权值为wemax=0.9,wemin=0.4,取初始权重we为0.9。学习因子满足ce1+ce2=4,且ce1为2时迭代次数较小,ce1在两端点0和4时迭代次数较大,出现对称性;在两端点出现搜索失败率较大。取ce1=ce2=2,根据需要的当前位置与最好位置之间的分辨率(精度)设置粒子最大速度为0.5。为防止连续迭代达不到收敛状态和观测的本文粒子群算法迭代收敛次数,确定算法最大迭代次数为200。参数设置完成后对数据进行训练和测试,得到各关节误差补偿值的预测与实际输出的变化,如图11~图17所示。
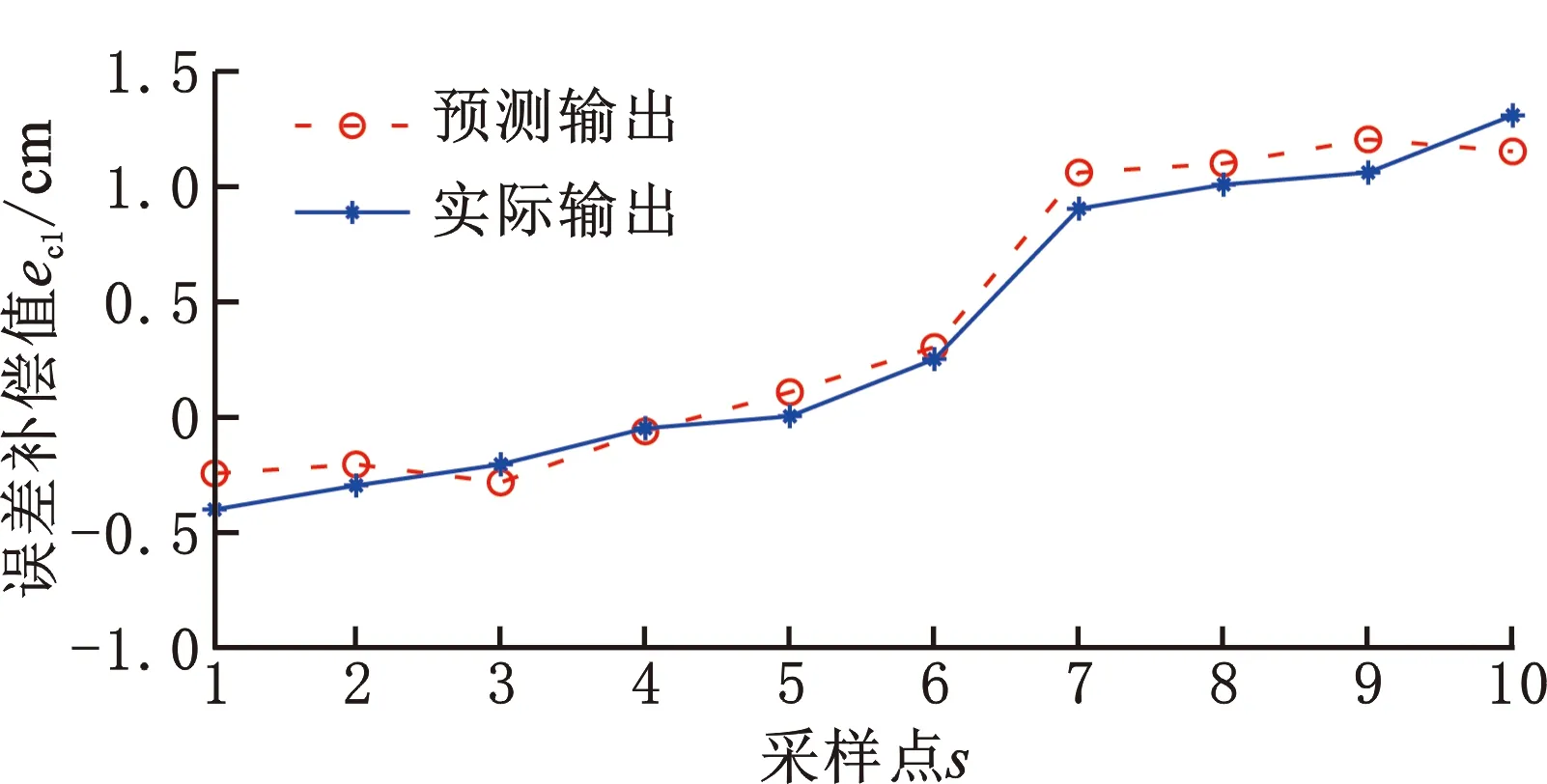
图11 关节1误差补偿值预测效果
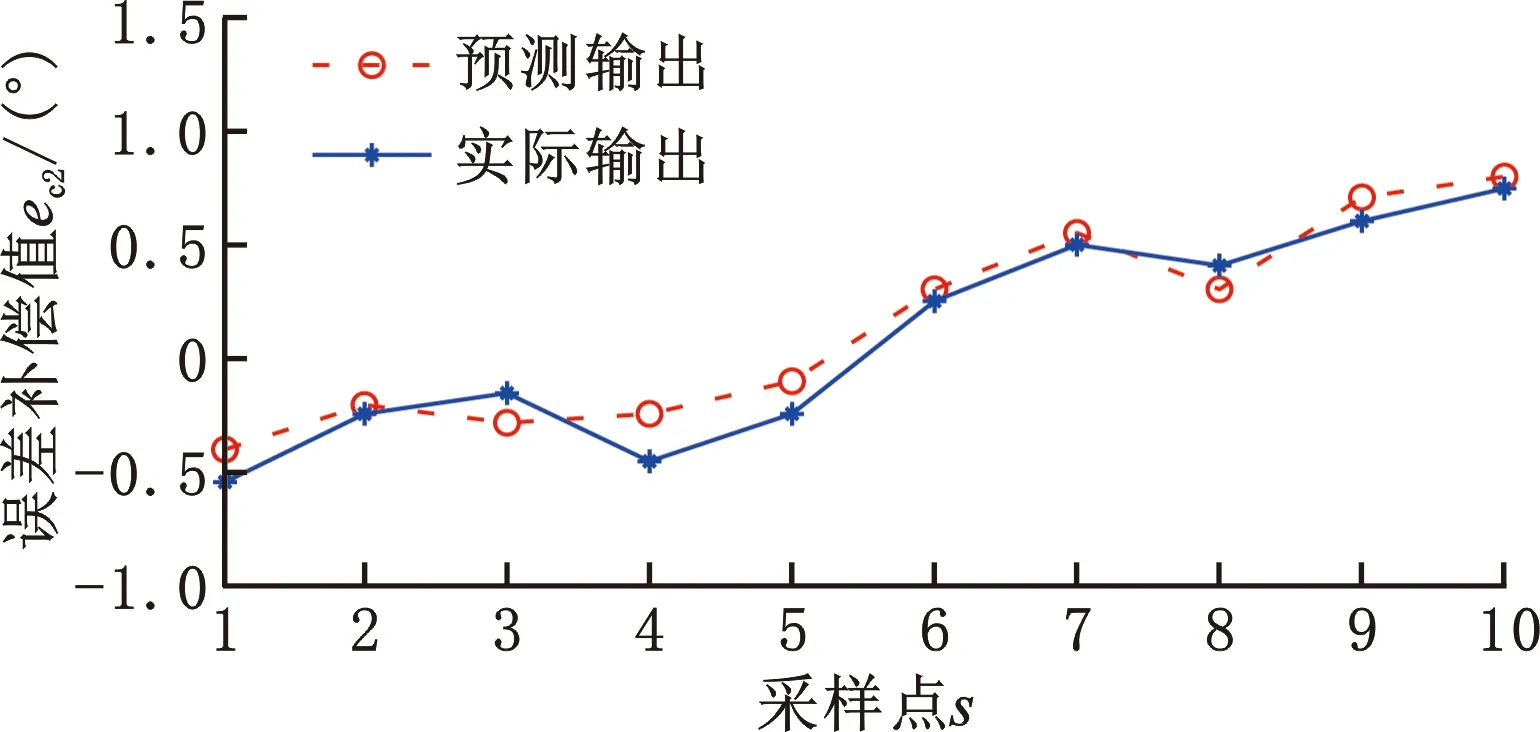
图12 关节2误差补偿值预测效果
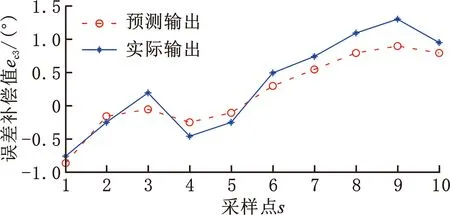
图13 关节3误差补偿值预测效果

图14 关节4误差补偿值预测效果
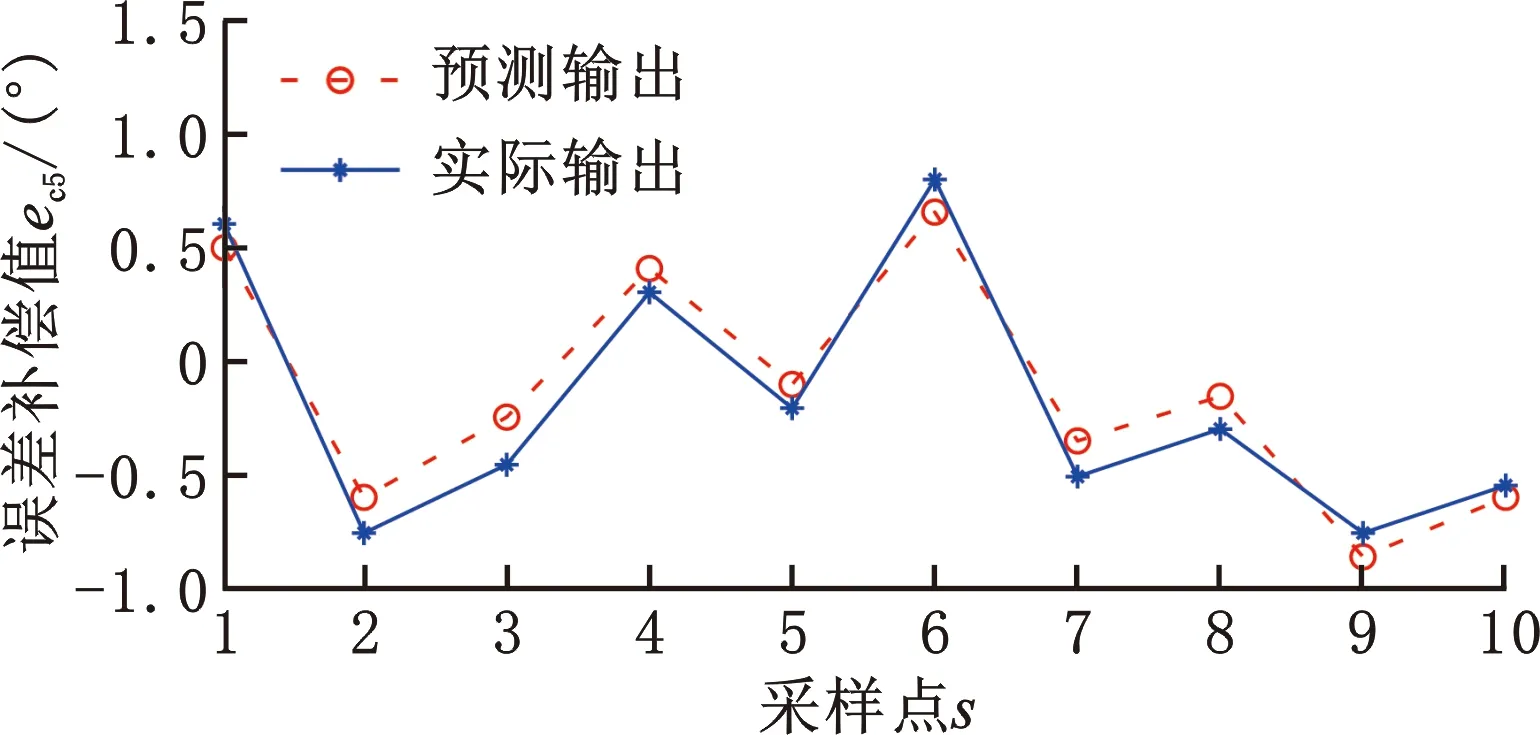
图15 关节5误差补偿值预测效果
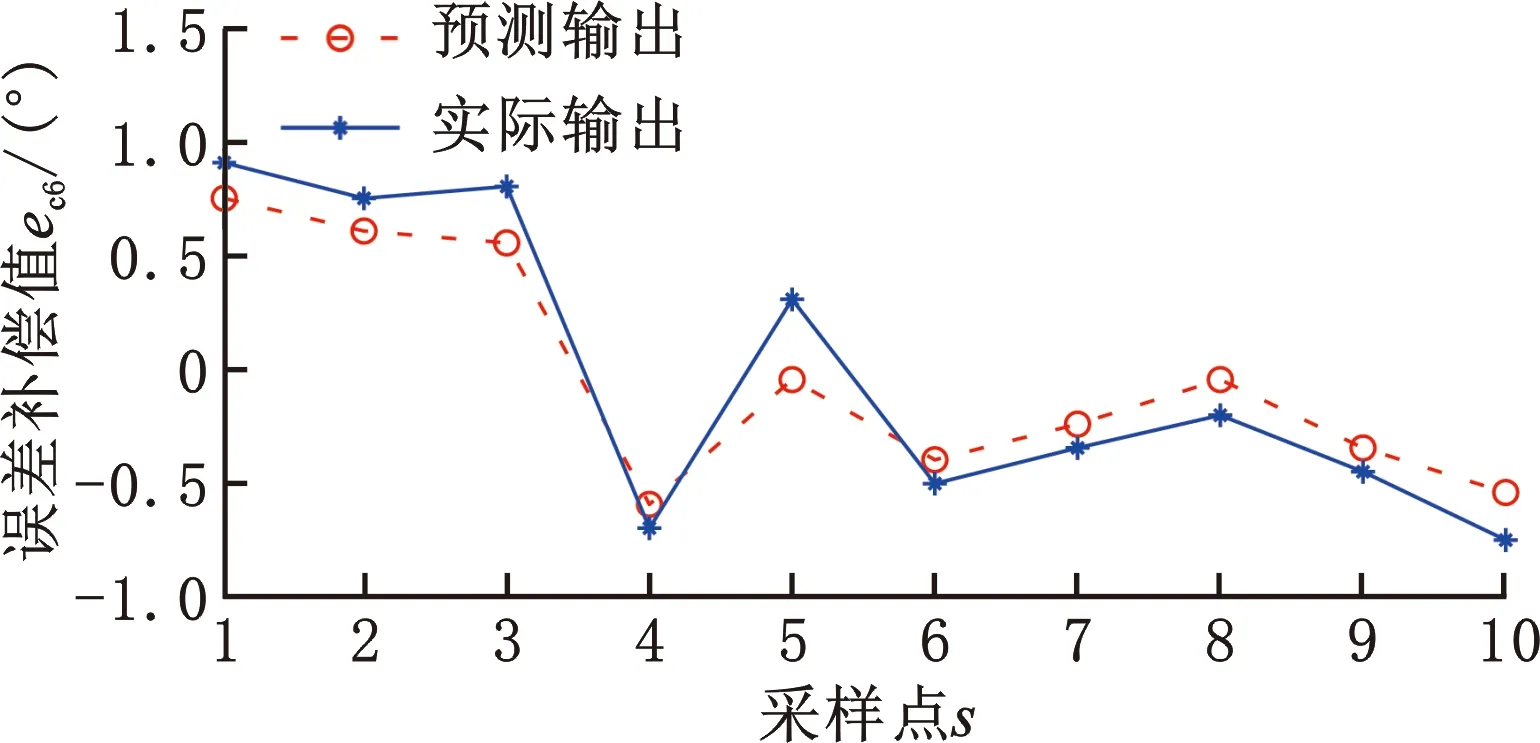
图16 关节6误差补偿值预测效果
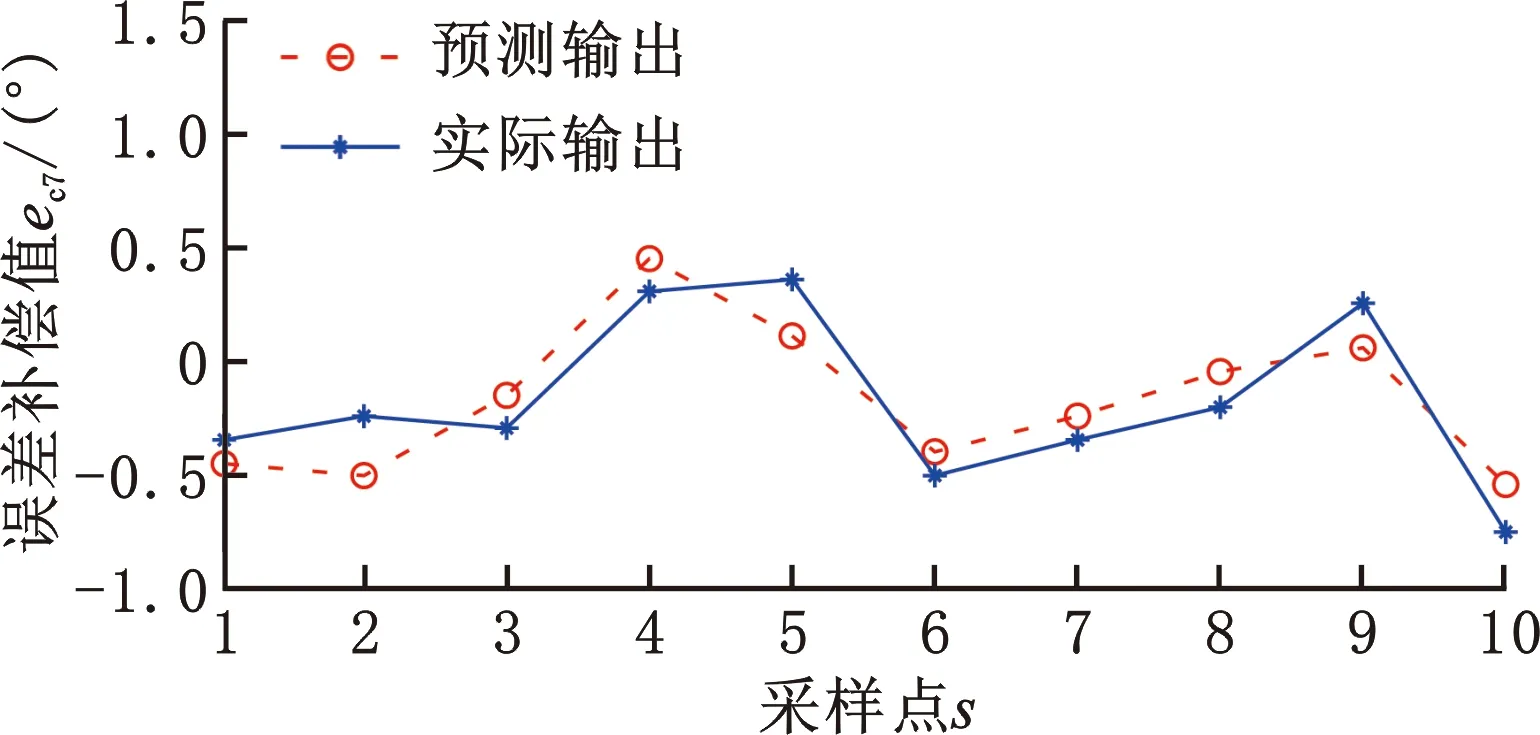
图17 关节7误差补偿值预测效果
4.4 GA-BP、PSO-BP、PSO-GA-BP算法预测数据的误差对比
分别建立GA-BP和PSO-BP算法的误差预测模型,经过数据集训练和测试得到GA-BP算法、PSO-BP算法与PSO-GA-BP算法的预测值和实际值之间的各关节绝对误差,如图18~图24所示。对比可知,PSO-GA-BP模型预测能力较高,预测值和实际值之间的误差较小,为七轴库卡机器人的误差补偿提供了较好的误差补偿模型。
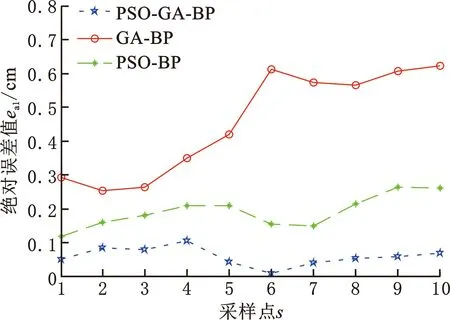
图18 不同算法对应的关节1输出误差绝对值
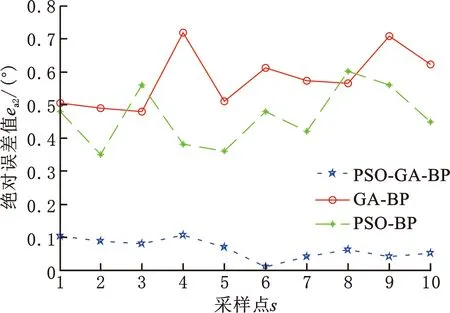
图19 不同算法对应的关节2输出误差绝对值
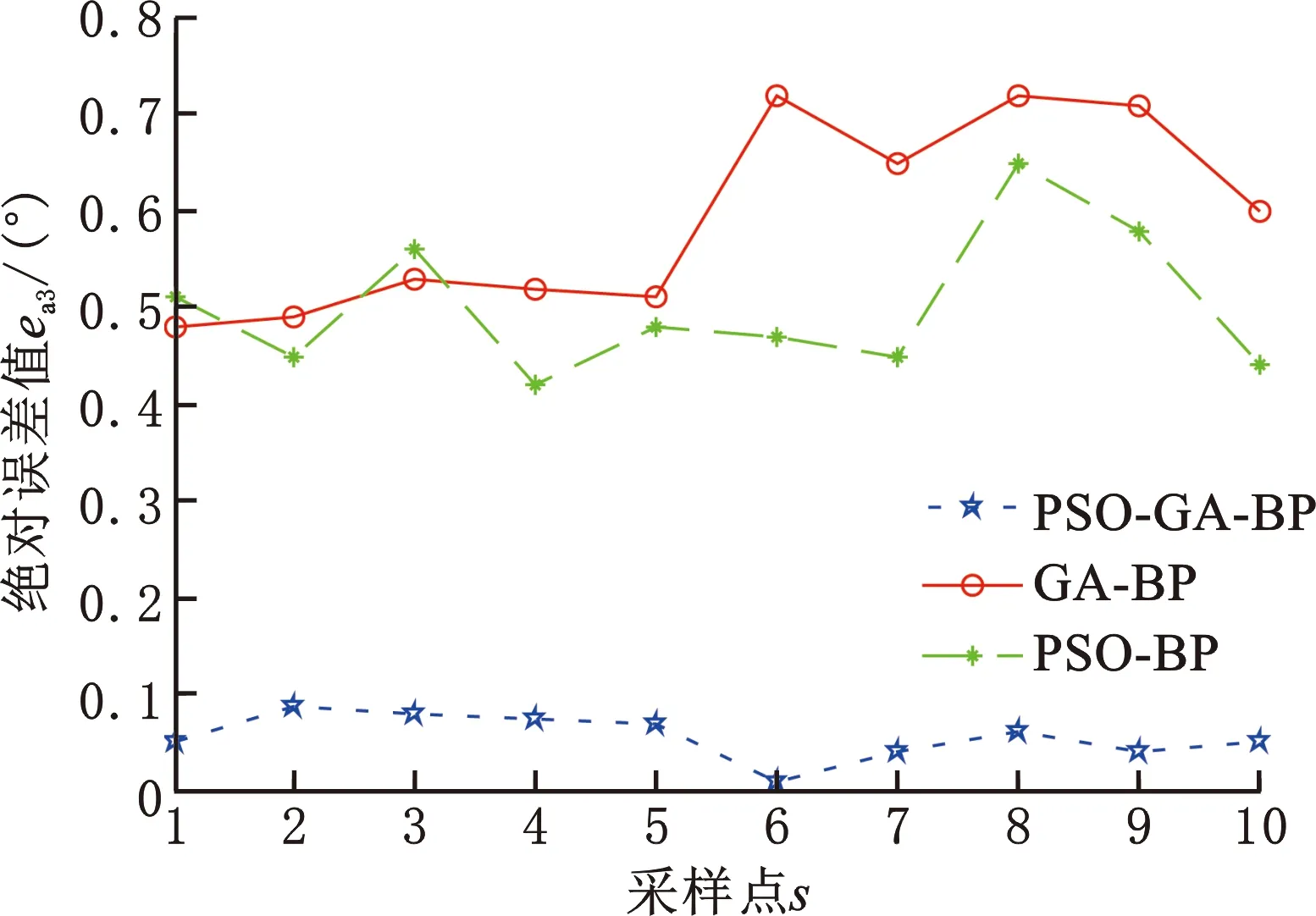
图20 不同算法对应的关节3输出误差绝对值
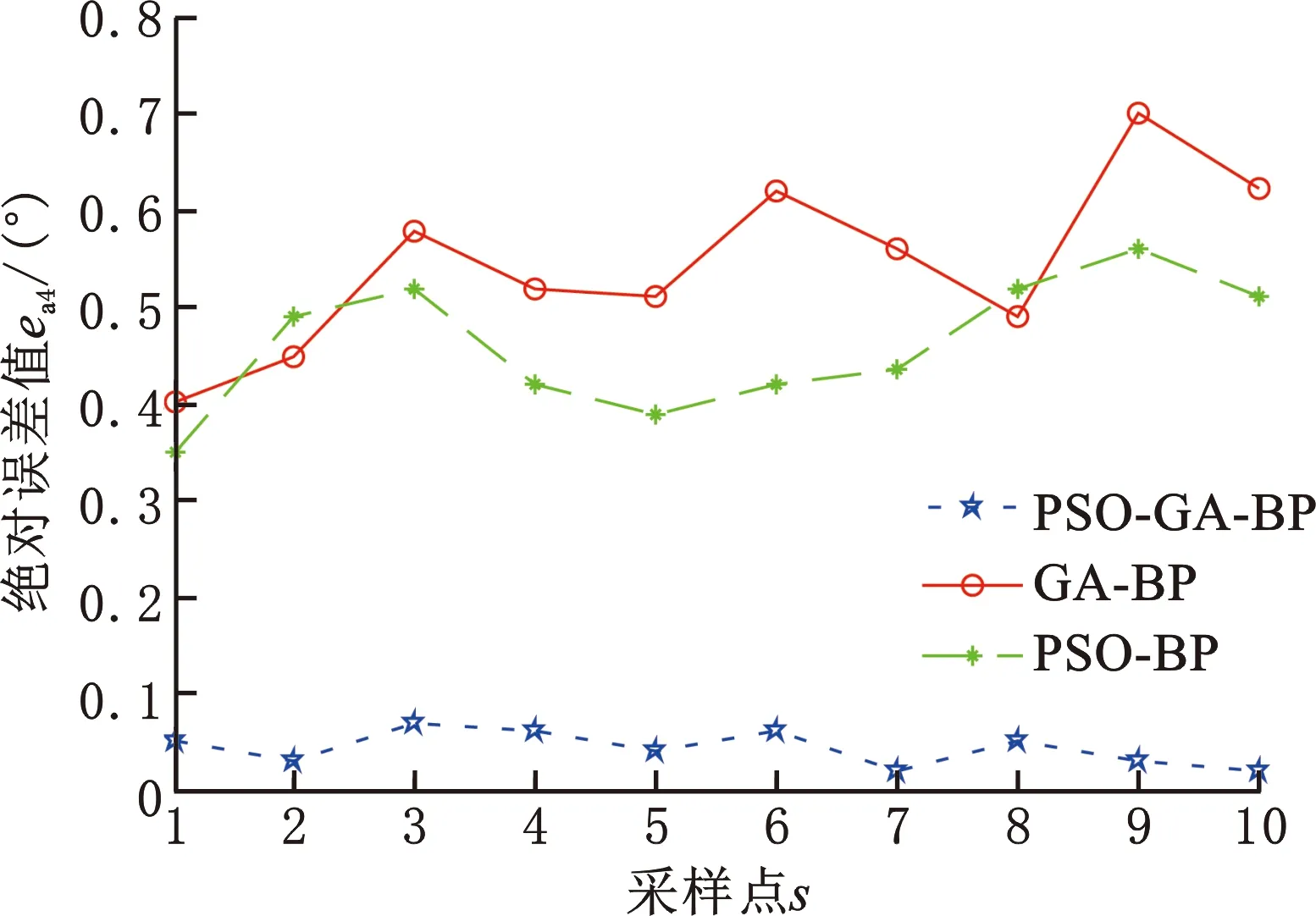
图21 不同算法对应的关节4输出误差绝对值
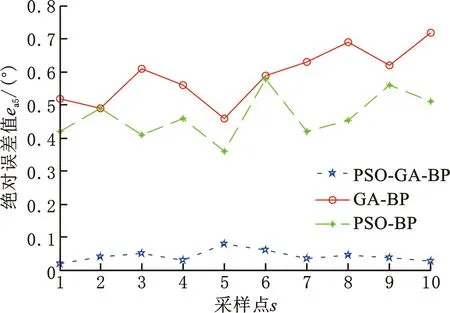
图22 不同算法对应的关节5输出误差绝对值
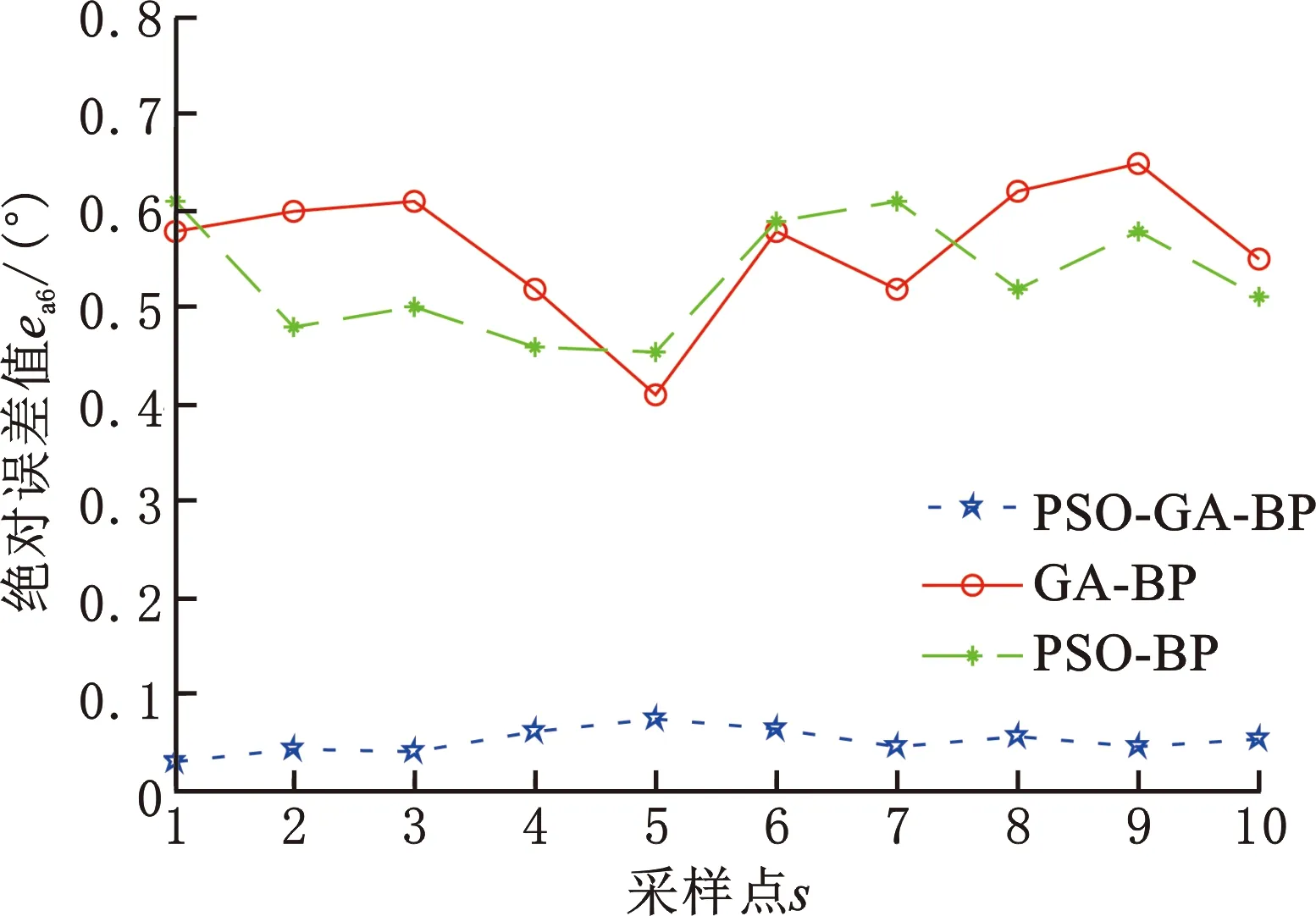
图23 不同算法对应的关节6输出误差绝对值
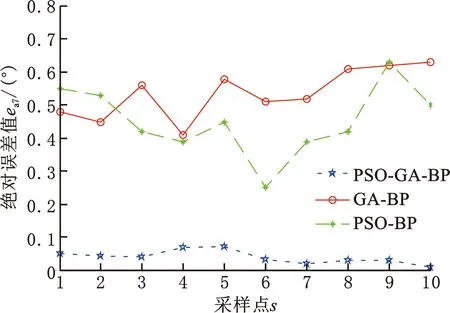
图24 不同算法对应的关节7输出误差绝对值
4.5 误差补偿与加工效果
本文通过上述分析得到机器人各关节误差补偿的预测输出,然后通过库卡机器人Workvisual 5.0软件对各位姿坐标进行误差补偿,减小机器人几何误差、系统误差及测量误差对机器人轨迹的影响,从而提高机器人的定位精度和轨迹精度。对机器人各位姿坐标误差补偿完成后,再次运用携带激光器的七轴库卡机器人对发射筒(箱)进行加工。误差补偿前后的机器人轨迹如图25所示,补偿前后的加工效果如图26、图27所示。
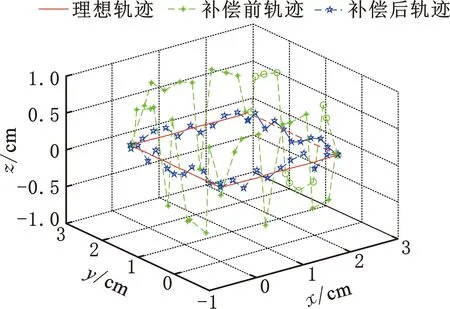
图25 机器人轨迹

(a)补偿前加工试验件正面图 (b)补偿后加工试验件正面图

(a)补偿前加工试验件侧面图
5 结论
(1)本文采用机器人正逆运动学数值计算方法来验证D-H机器人建模方式建立的七轴机器人模型,其计算结果和仿真结果对比发现,机器人位姿参数及各关节角度值误差最大分别为0.0003 m和0.0003 rad,证明了模型具有较高的正确性。
(2)本文采用Sage-Husa自适应卡尔曼滤波来解决系统噪声和测量噪声的模型不准确问题,实时更新估计突变噪声的均值、协方差,从而对模型参数和噪声特性进行实时修正,以减小误差,获得更高的估计精度。
(3)对GA-BP、PSO-BP、PSO-GA-BP算法模型的预测误差进行对比,结果显示PSO-GA-BP算法模型具有较高的预测精度,各关节的预测输出与实际输出的绝对误差最大为0.1 cm和0.1°。
(4)通过采用机器人软件对各关节的误差进行补偿,得到的机器人仿真轨迹误差减小约72%,切割实验表明所得到的加工件满足加工精度要求。
