基于土壤温、湿度记忆性的土壤湿度预测方法研究
2023-11-14魏森涛王澄海张飞民杨凯
魏森涛,王澄海,张飞民,杨凯
(甘肃省气候资源开发及防灾减灾重点实验室,兰州大学大气科学学院,甘肃 兰州 730000)
引言
作为陆地下垫面的主要组成部分,土壤不仅承载着陆地生态系统,还扮演着陆-气之间水分循环、能量平衡“调节器”的重要角色。土壤可以感知来自大气的异常变化信号,还可将这些信息反馈给大气,对水资源、农业和生态系统的时空演变有着重要影响。作为陆面过程研究的重要参量,土壤湿度在气候预测和全球气候变化研究中也起着至关重要的作用。土壤湿度通过改变地表蒸发和反照率、土壤热容量等物理属性以及植被生长状况等直接或间接影响局地及区域气候,还通过参与陆-气之间相互作用影响区域乃至全球气候。因此,土壤湿度既是气候变化的重要影响因子,也是反映地表水文变化的一个总体指标(王澄海等,2008)。通过研究土壤湿度的变化特性,可以更好地理解和提高对全球气候变化的认知水平(Shinoda and Nandintsetseg,2011;Seneviratne and Koster, 2012;Hagemann and Stacke,2015)。
在气候模式中,土壤温、湿度是模式下边界的重要物理量。然而,目前气候模式初始场中的土壤温、湿度多以多年平均值作为参考值,而边界场在大气场的强迫迭代下形成,需要较长的模式平衡时间(spin-up)并高度依赖于陆面过程模式和大气模式的耦合过程,往往偏差较大。近年来,随着机器学习方法的兴起完善,根据土壤温、湿度自身变化规律,建立土壤温、湿度变化的预测模型,预测未来时刻的土壤温、湿度变化,然后将其作为模式的下边界条件,已显示出广阔前景。同时,土壤温、湿度空间差异性较大,且观测站点相对稀少,机器学习建立的预测模型难以全面准确地获得土壤温、湿度空间信息,另外目前卫星观测反演的土壤湿度也存在较大误差。因此,利用机器学习的方法建立理想的土壤湿度预测模型,克服已有预测模型存在预测精度、泛化能力、多特征处理能力等问题,对提高预测性能有着重要的探索意义(Prakash et al., 2018;Cai et al., 2019)。
近年来,随着训练算法的优化、人工智能的快速发展,机器学习方法已成功应用于大气科学领域(Hinton et al., 2006),如降水、气温预测(陈浩等,2017;Cifuentes et al., 2020),厄尔尼诺/南方涛动预测(Guo et al., 2020),数值模式初边界条件、物理参数化方案构建(任萍等,2020)等。利用随机森林方法预测麦田土壤湿度,在0~20 cm和20~40 cm土层的预测精度达到88%以上,显示出机器学习算法在土壤水分建模预测中具有良好潜力(聂红梅,2019)。相比传统前馈神经网络在预测过程中会出现局部最小化及收敛速度慢的问题,深度学习方法采用多层隐藏层结构,增加了对大数据和多特征数据的分类和拟合能力;此外,深度学习方法在图像和序列处理方面有优势,对于呈指数级增长的地球系统科学数据可以通过深度学习进行信息挖掘。研究表明,引入卷积核的卷积神经网络(Convolutional Neural Networks,CNN),可以很好地捕捉图像中的信息(Lecun and Bengio, 1998),通过卷积核进行空间局部连接,将临近点之间相联系,能够有效提取要素分布的空间信息。与传统前馈神经网络对比,卷积神经网络方法表现出明显优势(Tan et al., 2019;Garcia, 2021)。卷积神经网络方法对ENSO指数预测(Ham et al., 2019)、东亚夏季风预测(Tang and Duan, 2021)方面也有出色表现。土壤湿度的空间差异明显,根据卷积神经网络方法可以自动学习土壤湿度空间分布特征与联系,对预测土壤湿度具有很好的潜力。
上述研究表明,利用机器学习进行土壤温、湿度预测,具有良好的潜力和广泛的应用前景。利用机器学习建立单独的土壤湿度预测模型,还可以获得较为精确的土壤湿度预测值,从而代替物理模型为大气模式提供初边界场。已有研究大多考虑预测变量自身变化信息建模,在土壤湿度预测建模时考虑土壤温度的影响,是否可以提高预测性能也是值得探索的问题。本文试图利用土壤湿度自身记忆性特征,基于卷积神经网络深度学习方法预测土壤湿度,探索提高未来月到季节尺度上土壤湿度预测性能。
1 数据和方法
1.1 土壤温、湿度数据
本文使用欧洲中期天气预报中心第五代(ERA5)全球再分析资料中的土壤湿度数据集,研究表明,该数据能很好地刻画土壤湿度的空间分布,其年际变化与观测值高度相关,对土壤湿度季节和年际变化的再现能力较优(王一昕,2019;宋海清等,2020)。为了数据统一和便于讨论,在基于卷积神经网络的土壤湿度预测模型构建中,将ERA5再分析土壤湿度数据视为真值并作为训练数据集。数据空间分辨率为 0.1°×0.1°,土壤温、湿度数据有4个垂直层,深度分别为0~7、7~28、28~100、100~289 cm。选用1961年1月至2020年12月的月平均数据建立神经网络模型,并对2021年1—12月的土壤湿度进行预报和验证。
以往研究在构建土壤湿度预测模型时忽略了土壤温度的影响,Wang和Yang(2018)将等温模型的CLM4.5进行了重构,建立了水热完全耦合的水热传输模式(Fully Coupled-Community Land Model,FCCLM),从而使得土壤水热耦合在理论上更加完备(杨凯,2017),获得了良好的效果。同理,在使用深度学习建立预测模型时不仅需要考虑土壤湿度自身变化信息,也需要考虑土壤温度的影响。因此,本文构建土壤湿度预测模型时选用土壤温、湿度作为预测因子。考虑到大气要素的记忆性较短,在预测月尺度的土壤湿度时暂不把反映大气要素的因子纳入到预测因子中。
所有数据均线性插值到1°×1°网格,研究范围为全球,共181个纬度格点,360个经度格点。为消除不同预测因子之间量纲和单位的影响,在进行数据训练之前,对所有数据进行归一化处理。
1.2 卷积神经网络方法
卷积神经网络是一种专门用来处理具有类似网格结构的数据方法,网络中至少有一层用卷积运算来替代一般的矩阵乘法运算。其核心是卷积层,卷积层功能是对输入数据进行特征提取,其内部包含多个卷积核,组成卷积核的每个元素都对应一个权重系数和一个偏差量,类似于一个前馈神经网络的神经元。卷积层内每个神经元都与前一层中位置接近区域的多个神经元相连,区域的大小取决于卷积核大小,称为“感受野”。卷积核工作时,会有规律地扫过输入特征,在感受野内对输入特征进行矩阵元素乘法求和并叠加偏差量。卷积核的大小、步长和填充共同决定卷积层输出特征图的尺寸,是卷积神经网络的超参数,其中卷积核大小可以指定为小于输入图像尺寸的任意值,卷积核越大,可提取的输入特征越复杂;卷积步长定义了卷积核相邻两次扫过特征图时位置的距离,卷积步长为1时,卷积核会逐个扫过特征图的元素,步长为n时会在下一次扫描跳过n-1个元素;随着卷积层的堆叠,特征图的尺寸逐步减小,因此填充是在特征图通过卷积核之前人为增大其尺寸以抵消计算中尺寸收缩影响的方法,常用的填充方法为按零填充和重复边界值填充。卷积运算定义如下:
式中:X和Y分别表示输入和输出矩阵;W为卷积核的权值矩阵;f为非线性激活函数,对卷积层的输出进行非线性变换,常用的激活函数有sigmoid、tanh和ReLu等;b表示偏置矩阵;i和j分别表示第i层卷积层第j个卷积核;k和l分别表示卷积核的宽度和长度。
卷积神经网络模型减少了训练参数的数量,并且能够保持空间邻域的局部特征。此外,卷积层的输入通常包括平均子采样和最大子采样形式,这样可以减少网络层之间的连接数,降低过拟合风险(Yosinski et al., 2014;周飞燕等,2017)。
1.3 回归拟合决定系数
把陆地上每一个格点作为一次预测,以预测值为横坐标,真实值为纵坐标作散点图,并计算回归拟合决定系数(R2)来直观对比模型对不同深度层土壤湿度的预测效果。回归拟合决定系数计算公式如下:
式中:n为格点数;f(xi)表示预测值;yi表示真实值;y¯表示真实值的平均值。R2越接近1,表示预测效果越好。
2 土壤湿度预测模型的构建
图1为基于土壤湿度记忆性特征建立的卷积神经网络土壤湿度预测模型基本原理。卷积神经网络包含4个卷积层,每层分别有128、64、32、16个滤波器,1个全连接层和1个输出层,每个滤波器的内核大小为5×5。输入层的变量对应于τ-5~τ月的土壤温、湿度(τ表示当前月),把τ+1到τ+6的土壤湿度作为输出变量。对每个卷积层特征映射的边界使用零填充,激活函数是漏校正线性单元(Leaky-ReLU)。为了防止过度拟合,每个卷积层后面都有一个超参数0.3的dropout层,即暂时随机移除30%的神经元。模型的自适应学习率为0.001。
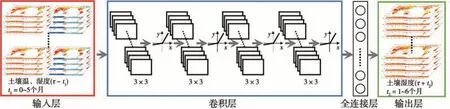
图1 土壤湿度卷积神经网络预测模型示意图Fig.1 The schematic of the convolutional neural network prediction model of soil moisture
在训练过程中,以1961年1月至2020年6月0~7、7~28、28~100、100~289 cm层深度的土壤温、湿度作为预测因子,以1961年7月至2020年12月上述4层土壤温、湿度作为模型逼近和预测对象。用前6个月的土壤温、湿度来预测后6个月的土壤湿度,每连续6个月的土壤温、湿度数据及后6个月的土壤湿度数据分组为一个样本,共709个样本,其中150个样本作为验证集,剩下的样本作为训练集。
图2为训练过程中损失函数变化情况,发现随着训练进行,训练集的损失函数逐渐下降,验证集的损失函数呈明显下降趋势,表明模型稳健且具有良好的鲁棒性能。
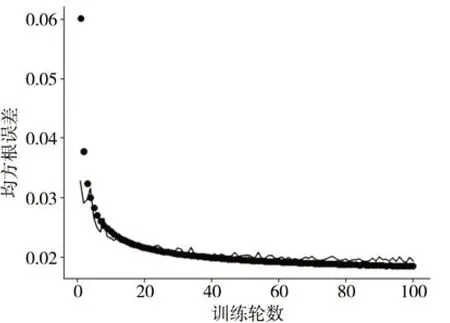
图2 训练数据集和验证数据集的损失函数Fig.2 The loss function of the training dataset and the test dataset
3 土壤湿度预测效果验证
为了检验土壤湿度预测模型的有效性,分别做两组试验:(1)使用2020年7—12月土壤温、湿度预测2021年1—6月土壤湿度;(2)利用2021年1—6月土壤温、湿度预测7—12月土壤湿度。通过比较两组试验,验证模型预测全年土壤湿度的可靠性。从预测和ERA5的2021年7—12月0~7 cm(图3)、7~28 cm(图4)、28~100 cm(图5)、100~289 cm(图6)深度层的土壤湿度差值发现,总体上预测误差大部分在0.05 m3·m-3以内,南北极地地区的预测误差在0.02 m3·m-3以内;热带地区预测误差大于中高纬度地区,且误差随着深度增加明显减小,在28~289 cm深度内预测误差几乎均小于0.02 m3·m-3。具体来看,7—12月随着时间变化,欧亚区域预测效果先变差后变好,北美区域预测效果整体较好,非洲、澳洲、南美洲区域整体上预测效果变差,且4个深度层的变化类似;从土壤浅层到深层,预测效果逐渐变好,其中0~7 cm和7~28 cm的预测效果变化不明显,28~100 cm开始预测效果明显变好,这是由于月尺度上的土壤湿度变化受大气要素变化影响的缘故。
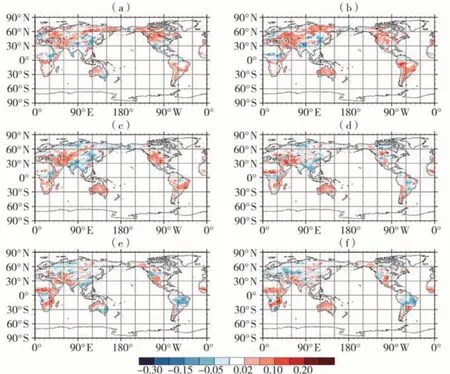
图3 2021年7—12月0~7 cm深度土壤湿度预测值与真实值差值分布(单位:m3·m-3)(a)7月,(b)8月,(c)9月,(d)10月,(e)11月,(f)12月Fig.3 The distribution of difference between the predicted soil moisture of 0-7 cm depth and the real value from July to December 2021 (Unit: m3·m-3)(a) July, (b) August, (c) September, (d) October, (e) November, (f) December

图4 2021年7—12月7~28 cm深度土壤湿度预测值与真实值差值分布(单位:m3·m-3)(a)7月,(b)8月,(c)9月,(d)10月,(e)11月,(f)12月Fig.4 The distribution of difference between the predicted soil moisture of 7-28 cm depth and the real value from July to December 2021 (Unit: m3·m-3)(a) July, (b) August, (c) September, (d) October, (e) November, (f) December

图5 2021年7—12月28~100 cm深度土壤湿度预测值与真实值差值分布(单位:m3·m-3)(a)7月,(b)8月,(c)9月,(d)10月,(e)11月,(f)12月Fig.5 The distribution of difference between the predicted soil moisture of 28-100 cm depth and the real value from July to December 2021 (Unit: m3·m-3)(a) July, (b) August, (c) September, (d) October, (e) November, (f) December
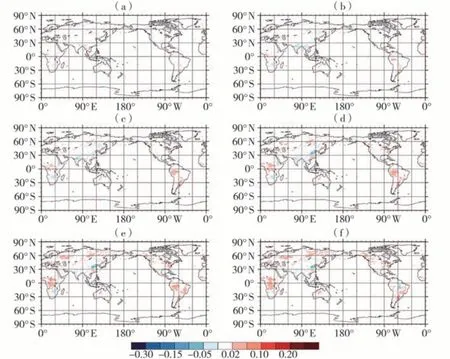
图6 2021年7—12月100~289 cm深度土壤湿度预测值与真实值差值分布(单位:m3·m-3)(a)7月,(b)8月,(c)9月,(d)10月,(e)11月,(f)12月Fig.6 The distribution of difference between the predicted soil moisture of 100-289 cm depth and the real value from July to December 2021 (Unit: m3·m-3)(a) July, (b) August, (c) September, (d) October, (e) November, (f) December
为检验模型对不同深度层土壤湿度的预测效果,绘散点图并计算回归拟合决定系数,图7为2021年1—6月不同土壤深度层的拟合结果。可以看出,0~7、7~28、28~100、100~289 cm深度层的决定系数R2分别为0.89~0.93、0.91~0.95、0.92~0.96、0.98以上,表明深层土壤湿度的预测效果优于浅层,且距起报时间越近预测效果越好。对比1—6月和7—12月(图略)预测效果,发现后者略好于前者,可能与北半球土壤湿度的记忆性在春季最长,与后期土壤湿度的关系更密切有关(李若麟等,2016)。

图7 2021年1—6月不同土壤深度层土壤湿度预测值和真实值的拟合关系Fig.7 The fitting relation between the predicted soil moisture with different depth layers and real values from January to June 2021
浅层土壤与大气的相互作用最为直接,也是陆-气相互作用的重要过程。研究表明,全球土壤湿度的记忆性变化在1~3个月,如北美南部、北非、中国北部、蒙古、南美南部以及澳大利亚等干旱区土壤湿度记忆性在1个月左右;北美东部、欧洲、西西伯利亚、亚洲南部以及刚果盆地等湿润区土壤湿度记忆性在2~3个月;青藏高原、伊朗高原、落基山脉、巴西高原以及南非高原等高山寒区土壤湿度记忆约2~3个月(李若麟等,2016)。因此,选取这几类区域浅层土壤湿度来验证模型的预测效果。选择中国北部、蒙古地区(73°E—123°E,32°N—52°N)及南美洲南部地区(50°W—70°W,20°S—32°S)两个区域作为干旱区代表,北美东部(60°W—80°W,50°N—60°N)、南非高原(17°E—33°E,22°S—35°S)分别代表湿润区和高山区,比较2021年7—12月0~7 cm深度层土壤湿度的真实值和预测值(图8)。可以看出,4个区域土壤湿度真实值平均分别为0.230、0.237、0.292、0.136 m3·m-3,预测的6个月土壤湿度平均值分别为0.215、0.254、0.298、0.140 m3·m-3,两者差值均在0.02 m3·m-3以内,这些区域在7—12月的预测效果均较好,表明建立的模型不仅能够预测连续的土壤湿度变化,而且能够较为准确地捕捉到土壤湿度变化的异常信号。
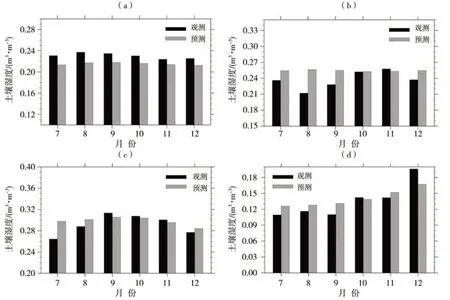
图8 2021年7—12月不同代表区域平均土壤湿度预测值与真实值变化(a)中国北部及蒙古,(b)南美南部,(c)北美东部,(d)南非高原Fig.8 Variation of mean values of predicted soil moisture and real values in different representative regions from July to December 2021(a) northern China and Mongolia, (b) southern South America,(c) eastern North America, (d) highlands of South Africa
目前关于机器学习预测土壤湿度的研究,以前主要在较小范围内开展。如利用随机森林方法对一个局域的麦田土壤湿度进行预测(聂红梅,2019),基于BP神经网络对草原土壤湿度预测(孙浩和吴梦碟,2023)等。本文将机器学习方法应用到全球土壤湿度预测上,并得到较好的效果,预测的土壤湿度可以作为全球气候预测模式的初始场和边界场。此外,土壤湿度作为干旱监测的重要指标,本文提出的方法也可以在未来应用于干旱的预测。
4 总结和讨论
本文基于EAR5再分析资料,利用土壤湿度的记忆性特点,并考虑影响土壤湿度的土壤温度,探索建立了基于CNN的土壤湿度预测模型,并对预测结果进行了验证。结果表明,本方法对月、季尺度上的土壤湿度具有很好的预测潜力。得到的初步结论如下:
(1)在土壤湿度预测模型中加入土壤温度作为预测因子,可提高预测效果。
(2)卷积神经网络模型可以有效提取土壤温、湿度的时空特征,可用于预测全球尺度较长时间的土壤湿度。其中,浅层土壤湿度预测误差大部分在0.05 m3·m-3以内,深层误差大部分在0.02 m3·m-3以内。
(3)基于土壤温、湿度变化信号建立的CNN模型可预测不同干湿区域土壤湿度的异常特征,预测误差平均在0.02 m3·m-3以内。
本研究提供了一种利用土壤温、湿度预测土壤湿度的方法,延长了预测的前置时间。虽然未考虑气象要素的影响,但仍然能够较好地预测土壤表层的湿度变化。一方面表明土壤温、湿度的变化更多来自与陆面自身的变化;另一方面也表明,建立的陆地下垫面土壤温、湿度变化的预测模型,可为大气模式提供初始和下边界条件,也可用于早期气候灾害如干旱、野火和洪水等的预警预测。
需要指出的是,土壤湿度的时间演变是一个复杂的动力过程,从理论上讲,加入更多的预测因子和更庞大的训练数据集可以提高其可预测性,未来研究将进一步探索。
