双变量多单元半全局极值搜索算法研究

张 雷，程春华

(1.武警海警学院舰艇指挥系，浙江 宁波 315801；2.海军航空大学，山东 青岛 266041)

0 引言

在实际控制系统中，输入和输出间往往存在某种未知的参考轨迹关系。这种关系表明，在输入作用下，系统的输出轨迹中会出现唯一的全局最优输出值（可能是极大值或极小值）[1]。如何使用适当的控制方法，让系统的输出始终保持在全局最优状态，这属于极值搜索算法研究的范畴[2]。

传统的极值搜索算法只考虑目标函数含有单个极值的情况。为了解决这个问题，Ying Tan 等基于简单极值搜索算法提出了1 种简单半全局极值搜索算法[3]。该算法采用平均化理论证明了半全局渐近稳定性，但该算法对目标函数和状态变量都有一些特殊要求，这在实际工程应用中很难满足[4-8]。因此，该算法的实际应用性受到一定限制。文献[9]融合多单元和半全局极值搜索算法，提出了用于静态系统的多单元半全局极值搜索算法，能够快速收敛至目标函数的全局极值。在此基础上，文献[10-11]还对目标函数含有2 个变量和3 个变量的情况进行了研究。文献[12]对单变量多单元半全局极值搜索算法进行了扩展，以应用于动态系统，并且给出了稳定性证明，但仍局限于单变量系统研究。

随着对极值搜索算法的深入研究，人们将数学优化算法和导数估计算法、参数估计算法等相结合，得到了各种类型的极值搜索算法[13]。目前，极值搜索算法仍在不断创新，如无限维抛物线偏微分方程系统的梯度极值搜索[14]、时变时滞系统的未知高阶导数最大化[15]、控制方向未知的滑模极值搜索[16]、基于李括号逼近的极值搜索[17]、基于合作并行学习的极值搜索[18]等。这些方法采取了滑模控制、参数估计等控制方法，为本文研究提供了参考依据。

本文综合文献[12]的稳定性分析方法和文献[16]的控制律设计思路，将双变量多单元半全局极值搜索算法扩展到动态系统，提出了1 种新的李亚普诺夫函数，并针对动态系统进行了算法稳定性证明，解决了传统双变量多单元半全局极值搜索算法仅适用于静态系统的问题。最后，基于通用多极值测试函数进行了数字仿真研究。

1 算法分析

在系统单元的动态优化问题中，需要对其进行数学建模。具体来说，可以对系统单元的动态行为进行数学描述：

式（1）中：x ∈ℝn为系统状态；um∈ℝ2为系统输入；y ∈ℝ 为系统输出；f 、h 为光滑函数，分别代表状态方程和输出方程。

针对无约束的情况，假设2 个动态系统组成的单元完全相同，分别为单元a 和单元b，u1a和u2a为单元a 的两输入，u1b和u2b为单元b 的两输入。

假设两动态单元的控制律为：

式（2）中：α(· ,·) 是光滑函数；ua∈ℝ2、ub∈ℝ2是输入变量向量组。

将式（2）代入式（1），可得到两单元的闭环系统：

以下是两单元动态单元系统需要满足的3个假设条件。

假设1：存在某光滑输入u：ℝ2→ℝn，使得

成立。

假设2：任意u ∈ℝ2，系统（3）将渐近收敛至其平衡点x=u 处。

假设3：对于式（1），定义Q(·) =(h ∘u )，存在唯一的全局最大值。其对应的∈ℝ 和∈ℝ 使下式成立：

双变量多单元半全局极值搜索算法主要思想是引入2 个完全相同的单元a 和单元b，使双变量沿着圆周搜索全局极值，将最优值保持在所搜索的圆内，并单调减小圆的半径至0，趋使u1、u2沿圆周向目标函数收敛至全局最优值所对应的输入值附近。双变量多单元半全局极值搜索算法结构见图1。

双变量多单元半全局极值搜索算法中，参数间隔会逐渐减小到接近于0，这个过程不是根据梯度来确定步长，而是通过调整参数间隔来实现的。在算法开始时，参数间隔会先按照预设形式进行设置，然后慢慢缩小。现分3步给出算法自适应律。

第1步：沿着圆周进行对比搜索。

考虑圆心为输入值(u1,u2)，半径为r 的圆，多单元半全局极值搜索算法沿着半径不断缩小的圆周反复搜索全局极值，θa和θb为两单元输入的夹角。

2个单元的输入为：

沿着圆周搜索的自适应律为：

式（8）～（10）中：Δθ为θa和θb之间的夹角；βθ＞0 是影响Δθ下降速度的参数，即沿着半径为Δ、角度为θ 的圆周搜索最优值；Δθ下降周期T 是提前设定递减至εθ的，周期为，

其搜索过程如图2所示。

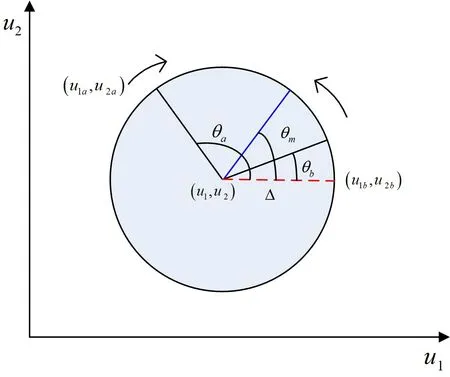
图2 沿全局优化点收缩圆的半径变化过程Fig.2 Changes of contraction circle radius along global optimal point

第2步：递归全局优化。

设i(i=0,1,2,…) 代表第i 次迭代，每次迭代开始，Δθ初始值都重新选取为到π，以使确保搜索轨迹为完整的圆周。θ 初始值选取为优化点为圆心的圆内的一点。在开始迭代时，i=0，θm0初始值设为0。第m次迭代中，θmi根据前一次θa和θb的值进行计算，算法表示如下：

沿着圆周进行搜索的过程以T 为周期反复搜索，θmi将在εθ=0 时的第i-1次迭代收敛至最优值。

第3步：减小圆的半径。

假设全局可行优化点位于初始圆内，即初始输入(u1( 0 ),u2( 0 ))为圆心，r( 0 )为半径的圆内，并且半径单调递减至0。

式（13）中：β ＞0 是决定r 递减速度的参数。当r 递减至某个极小的值ε 时，算法停止搜索。这意味着算法总的搜索时间为：

式（15）中：θmi与式（12）中的迭代值相关，则以r 为半径，(u1,u2)为圆心按自适应律（15）使圆紧缩过程中可确保能搜索到全局极值。保持(u1m,u2m)在同一个圆内，使(u˙1m,u˙2m)=( 0,0 )，自适应律为：

沿着圆周进行全局优化紧缩过程如图3所示。圆的圆心随着r 的递减收缩至非线性目标函数的全局极值点。

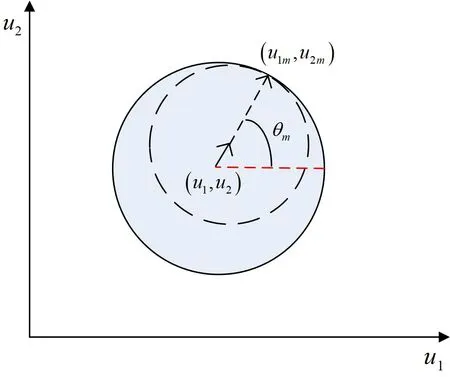
图3 沿着圆周进行全局优化过程Fig.3 Global optimization process along circle

注1：为了能够在系统中运用双变量多单元半全局极值搜索算法，控制参数必须满足条件β ≪βθ，βθ决定沿圆周搜索速度，β 决定半径收缩速度，即沿圆周搜索速度较快，半径递减速度较慢。

同一动态系统单元的输入u1和u2不断自适应变化的同时，系统动态也不断演化，且满足如果系统响应稳定且快速，那么在系统状态从初始状态到稳定状态的变化过程中，可以近似地认为这个过程是瞬间完成的，也就是说状态误差ξ=x-xˉ的收敛过程是瞬间完成的。由假设1 和假设2 可知，当系统达到稳定状态时，存在成立。给定系统动态x和其对应的稳定状态xˉ，则有：

如果系统响应稳定且迅速，那么系统状态从初始状态到稳定状态的收敛时间会非常短，则可以认为x ≈演化速度非常快，即h( x )≈演化速度非常快。为达到此目的，系统动态需要满足一定的假设条件。

假设4：针对动态系统（1），存在Lyapunov 函数W(ξ,u1,u2)，满足，

式（18）中：c1～c5为固定正值；为使ξ 满足式（17）的可行域；U 为使u 满足假设1 至假设3 的输入可行域。

注2：双变量多单元半全局极值搜索算法的主要优点在于收敛时间较短，且无输出颤振。其不足点为假设两单元完全相同，这是一较强的假设，另外对动态系统的动态特性要求也较为严格。

引理1[10]：考虑如图1所示的双变量多单元半全局极值搜索算法，采用公式（6）～（16），且系统满足以下条件。

假设5：系统存在初始值和初始间隔，使ε=0 ，εθ=0，目标函数h( x )存在唯一的全局最大值，参数β和βθ满 足β ≪βθ， 同 时 满 足

2 稳定性分析

接下来，对算法的稳定性进行分析，选取Lyapunov函数为：

由式（19）可知，系统稳定性的主要影响因素为(uia-)、(uib-)、ξa和ξb，其中，i=1,2。系统稳定时，有ui=和ξa=ξb=0 ，此时V=0 ，其中，i=1,2 。 进 一 步 由 假 设 4 中 的c1‖ ξ‖2≤W(ξ,u1,u2)≤c2‖ ξ‖2，c1和c2是固定正值，同时成立，知V ≥0 成立，且只有系统到达稳定状态时，有V=0 。从而，证明了V( u,ξ )的正定性。

将式（17）代入式（19）后，对式（19）微分可得：

将式（18）代入式（20）可得：

对式（21）化简，可得：

将式（8）～（16）代入式（6）（7）可得：

由式（8）～（10）可得：

当ha( x )＜hb( x )时，由式（12）可得θmi=θa，由式（23）～（28）可得u˙1a=0、u˙2a=0，即‖ ξa‖=0 成立，代入式（22），可得：

当ha( x )＞hb( x )时，由式（12）可得θmi=θb，由式（23）～（28）可得u˙1b=0、u˙2b=0，即‖ ξb‖=0 成立，代入式（22），可得：

由式（31）可得：

由式（17）可得：

由式（31）（33）可得：

对式（34）积分可得：

综上所述，可以得到如下定理。

定理1：假设系统满足假设1 至假设5，且控制律采用式（6）～（10），则式（1）所示的优化问题中，如果选择输入初始值使得满足假设5，则有以下结论。

1）双单元状态误差和输入误差均收敛至系统原点的某邻域：

2）以下不等式成立：

3 仿真分析

两单元输入单输出系统的状态方程为：

式（39）中：x1、x2、x3和x4为系统状态变量；和为输入量。单元a 选用控制律=20(u1a-x1) -9x2与=35(u2a-x3)-15x4；单元 b 选用控制律为=20(u1b-x1) -9x2与=35(u2b-x3)-15x4。选取通用典型双变量目标函数Ackley函数进行仿真验证。

当u1=u2=0 时，两单元的状态x1=x3=0，其目标函数含有唯一全局极小值min h(x1,x3)=0。双变量目标函数轨迹如图4所示。

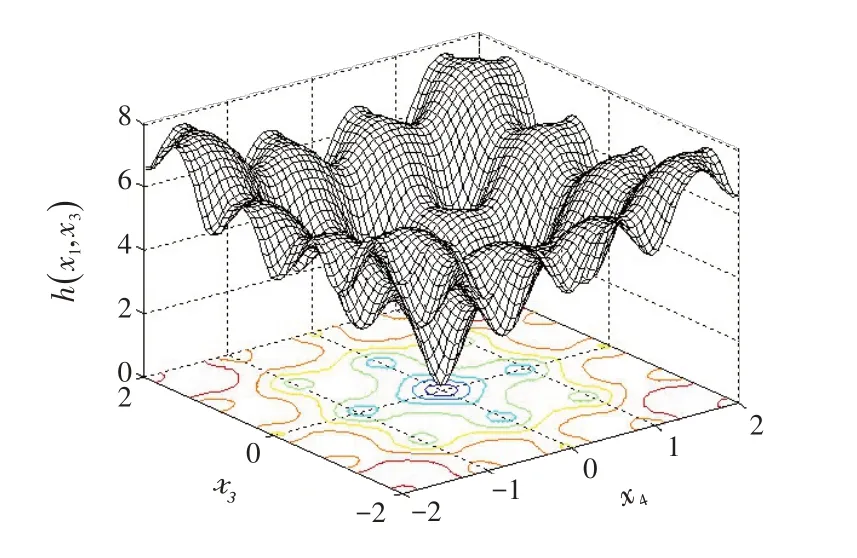
图4 目标函数轨迹图Fig.4 Objective function diagram

系统初始条件分别为x1( 0 )=3 、x2( 0 )=0 、x3( 0 )=-2 、 x4( 0 )=0 、u1( 0 )=-1 、u2( 0 )=-2 ，Δ初始=5。全局最小值位于(u1( 0 ),u2( 0 ))为圆心，r0=5 为半径的圆内，参数 β=0.03 、βθ=2 ，θ( 0 )=0 ，ε=εθ=0.001。当系统达到u1=0、u2=0 时，两单元的状态达到x1=0、x3=0，此时目标函数收敛至全局最小值。

使用双变量多单元半全局极值搜索算法，对方程组（39）（40）描述的系统进行仿真验证。单元a 的状态x1如图5所示；单元b 的状态x1如图6所示；单元a的状态x3如图7所示；单元b 的状态x3如图8所示；单元a 的u1a和u2a沿圆周变化轨迹如图9 所示；单元b的u1b和u2b沿圆周变化轨迹如图10 所示；u1和u2轨迹如图11所示；圆心轨迹如图12所示。

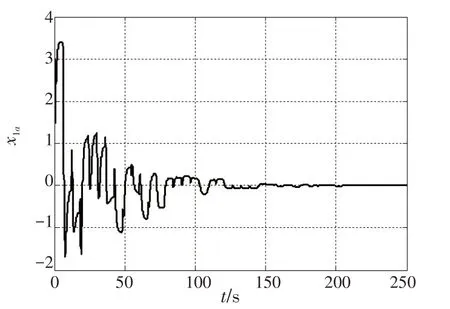
图5 单元a 的状态x1 仿真图Fig.5 State x1 simulation result of unit a

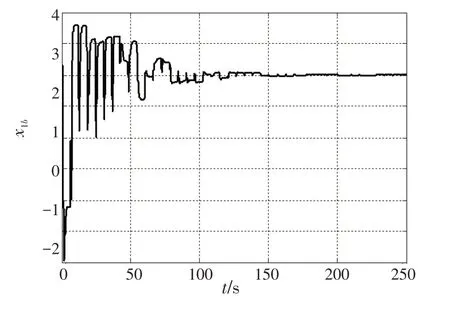
图6 单元b 的状态x1 仿真图Fig.6 State x1 simulation result of unit b

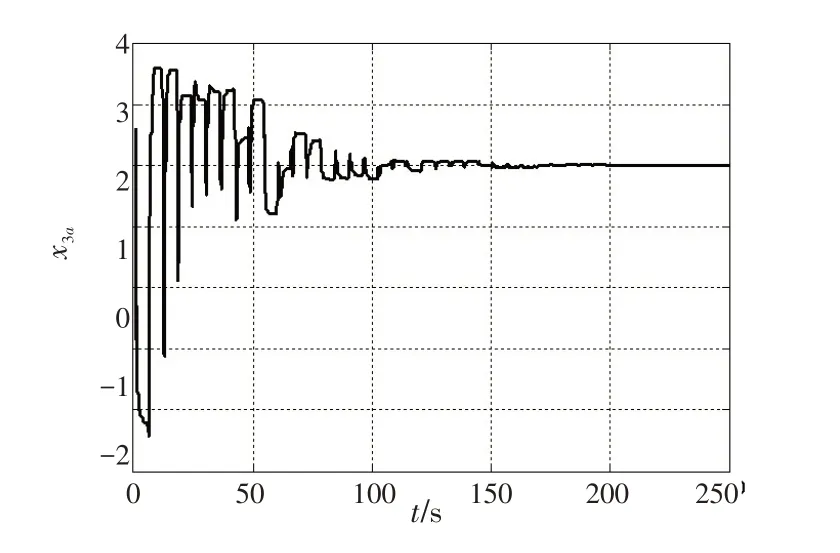
图7 单元a 的状态x3 仿真图Fig.7 State x3 simulation result of unit a

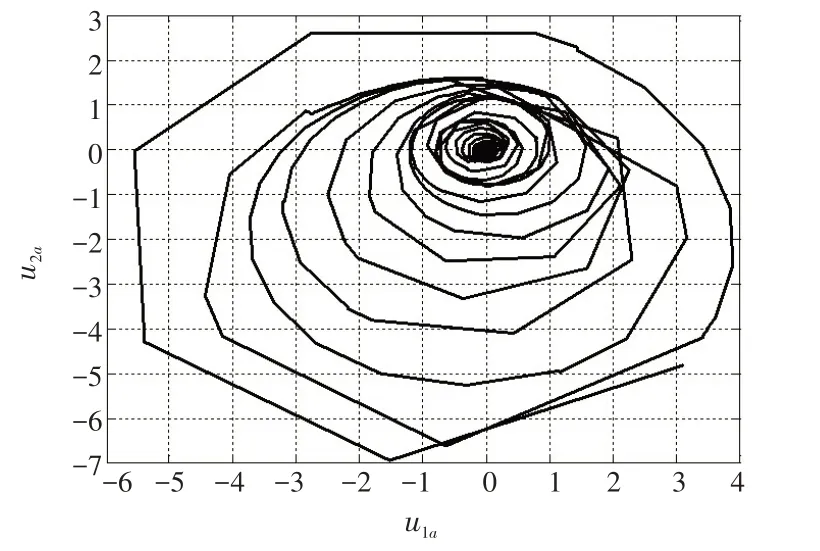
图9 单元a 的u1a 和u2a 沿圆周变化轨迹图Fig.9 Diagram of trajectory changes of u1 and u2 along circle for unit a

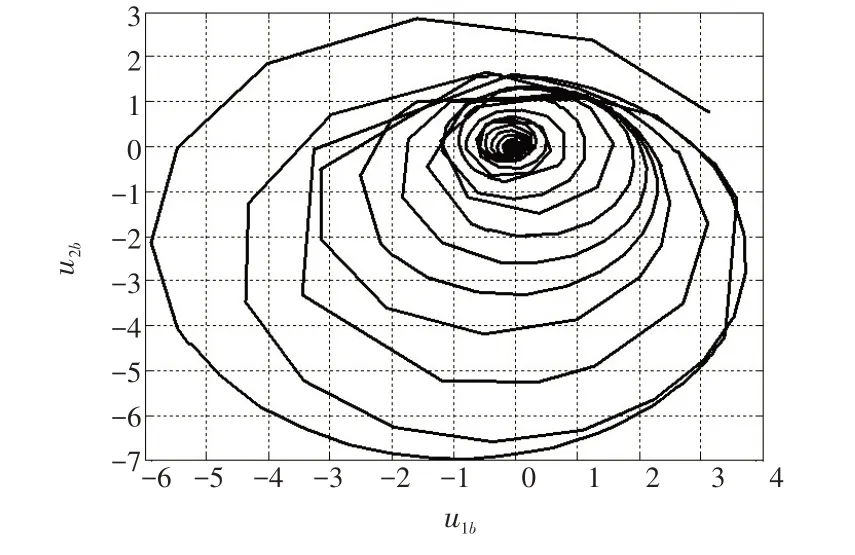
图10 单元b 的u1b 和u2b 沿圆周变化轨迹图Fig.10 Diagram of trajectory changes of u1 and u2along circle for unit b

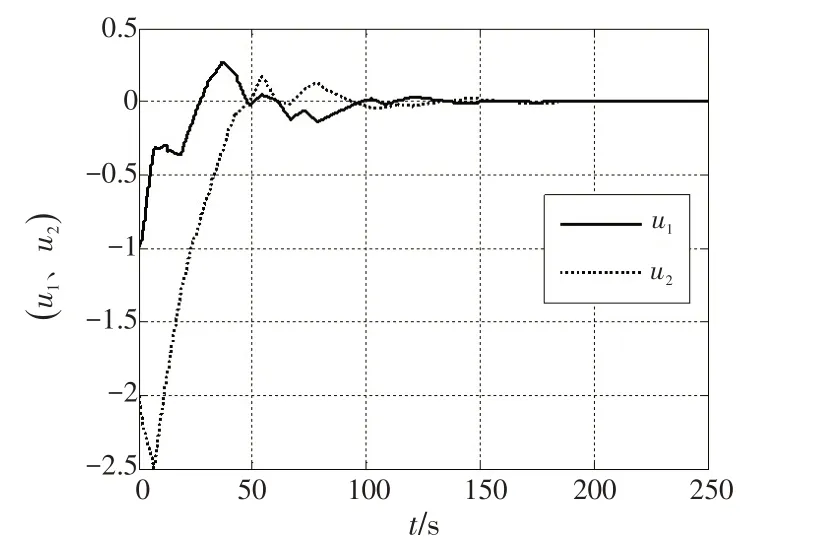
图11 u1 和u2 轨迹图Fig.11 Diagram of trajectories of u1 and u2

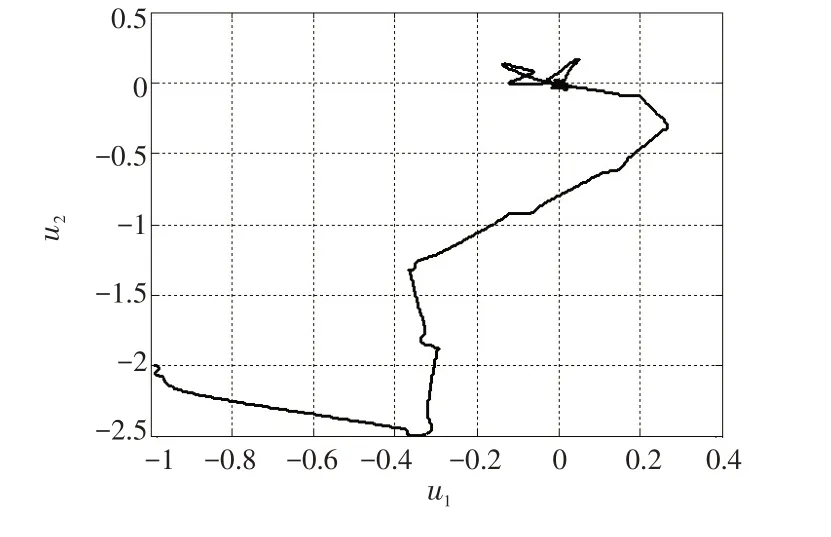
图12 圆心轨迹图Fig.12 Diagram of trajectories of circle center

通过图5～12 所示仿真结果可知，单元a 和单元b的状态x1和x3最终都达到了最优状态。单元a 的u1a和u2a沿圆周顺时针变化最终收敛至( )0,0 点；单元b的u1b和u2b沿圆周逆时针变化最终收敛至( 0,0 )点。u1和u2也各自达到了最优值，圆周的圆心最终达到( 0,0 )点。两单元的目标函数最终达到了全局最小值min ha(x1,x3)=hb(x1,x3)=0。

4 结论

本文突破多单元半全局极值搜索系统针对单变量进行研究的局限，对双变量系统进行研究，综合滑模控制和极值搜索控制方法进行控制律设计。利用单元的输入和动态误差项构造李亚普诺夫函数，证明了本文算法适用于动态极值搜索系统，基于通用多极值测试函数进行了数字仿真研究也证明了本文方法是可行的。