环氧粘结材料释气特性的模型建立与分析

许高斌,袁婷,关存贺,李明珠,冯建国

(合肥工业大学 微电子学院,安徽 合肥 230601)

大部分微机电系统(Micro-Electro-Mechanical System,MEMS)器件内部均包含真空腔或可动结构和部件,如微加速度计,只有采用真空封装才可以使其获得更好的工作性能[1]。在MEMS 封装中,MEMS 传感器采用真空封装可以降低能量消耗,减轻空气阻尼对器件性能的影响,大幅提高MEMS 传感器的长期可靠性[2]。

释气是指存在于材料表面或内部的气体或液体由于外部刺激(例如温度升高)释放到MEMS 真空腔中。由于气体会从散装材料或内部材料的表面层连续释放,因此在整个MEMS 传感器的工作寿命期间,室温下也会发生释气。当存在这种类型的释气时,内部腔体压力将在传感器工作过程中缓慢增加进而影响器件的寿命。

生物医学、消费电子、航空航天等应用领域对真空有着超高需求,材料的释气特性成为选用真空封装材料的重要参考指标,目前世界各国对材料的研究主要集中于测量真空下各种材料的放气率[3]。2015 年兰州空间技术研究所董猛等[4]釆用静态升压法成功实现了2 种吸波材料的放气率及其气体组分测量。2021 年史文龙等[5]在相同温度、不同时间的固化过程中对环氧粘结材料的放气特性进行了研究。国外Kwon 等[6]从理论和实验两方面考察了真空隔热板的核心材料聚碳酸酯的放气特性,得到了聚碳酸酯中溶解气体的总量和各种气体在聚碳酸酯中的扩散系数。

目前国内外学者主要集中于对不同材料本身在特定真空环境下的释气特性研究对比,通过横向对比不同材料之间的差异进而评估它们的性能,而鲜少对特定材料应用在具体器件上的性能退化进行分析。考虑到MEMS 传感器的体积普遍较小,外界温度的变化对于封装中常用的环氧粘结材料的表面吸附、解吸和扩散释气等影响显著,从而可能影响MEMS 传感器腔体内的真空度,降低器件的可靠性,本文针对市面上应用较为广泛的MEMS 传感器真空腔内的环氧粘结材料进行了释气特性评估。

本文以MEMS 传感器真空封装常用的环氧粘结材料为例,结合菲克扩散模型,为方便研究将环氧粘结材料看作一定厚度的平板,通过一维简化建立了不同温度作用下的释气速率随时间变化的理论数学模型。借助史亚刚等[7]在实验中测量的真空腔内的真空度数据,通过MATLAB 对实验数据进行拟合分析,验证了模型的准确性和适用性,为MEMS 传感器的封装可靠性分析提供了重要的研究基础。

1 理论研究及模型建立

1.1 材料释气特性的理论分析

任何固体材料在生产过程中的外界环境下都能吸附和溶解某些气体,当这些材料被置于真空环境中时,原有的动态平衡被打破,导致之前吸附的气体在材料表面以及内部进行扩散解溶,引发材料释气。

对一般真空设备来说,材料的释气是真空腔最主要的气源。材料的释气来源于两方面: 一是材料表面吸附气体的解吸。在MEMS 传感器真空封装中,往往会有一些气体吸附在贴片胶、腔体内部、键合材料、芯片和表面上。这些吸附气体经过真空烘烤等步骤可以在较短时间内去除,因此可忽略吸附气体的影响;二是材料内部溶解气体的扩散解溶。因环氧粘结材料易吸水的特性,相较于MEMS 器件封装内部的其他材料,内部溶解的水汽较多,需要很长时间才能将水汽去除,是材料释气的最主要来源[8],因此本文主要研究环氧粘结材料内部溶解气体的扩散释气。

一般情况下,气体在固体中的溶解度相对较小,因此有近似理想溶体的性质。由亨利定律可知,在一定温度下,固体中溶解的气体浓度与外界环境的气体压强成正比,外界压强越大,溶解的气体数量越多,即:

式中:C为固体中溶解的气体浓度;s为气体在标准大气压下的溶解度;p为外界的气体压强。

1.2 扩散释气模型的建立

粘结材料又称粘合剂,主要是由环氧树脂和其他添加剂组合而成。环氧粘结材料具有绝缘强度高、化学稳定性好、环境适应性强等特点,作为成型和密封材料广泛应用于MEMS 传感器中。

研究表明MEMS 传感器真空腔内环氧粘结材料的水汽释放过程基本符合菲克扩散模型[9]。扩散释气模型认为材料的释气机理是一个扩散过程,释气的过程由扩散速率决定。实际封装中使用的环氧粘结材料的厚度是有限的,因为扩散系数较小,一般情况下,气体分子在固体材料内的渗透是不稳定的,基本符合菲克第二定律,即:

式中:t为扩散时间;D为扩散系数。

将MEMS 传感器中的环氧粘结材料看作一定厚度的平板,其气体释放特性可以按平板的释气问题加以讨论。假设环氧粘结材料为厚度d的一块平板,如图1 所示,C0是材料的初始气体浓度,环氧粘结材料只有一面处于真空腔中,故只讨论一维方向的材料释气问题。

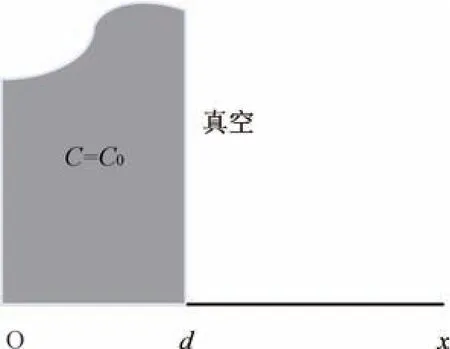
图1 有限厚平板材料释气模型Fig.1 Outgassing model of finite thickness plate material

则(2)式可简化为:

根据假设,初始条件和边界条件如下。

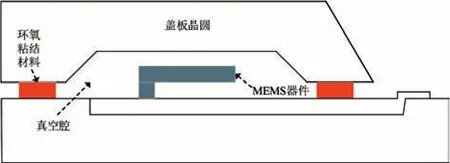
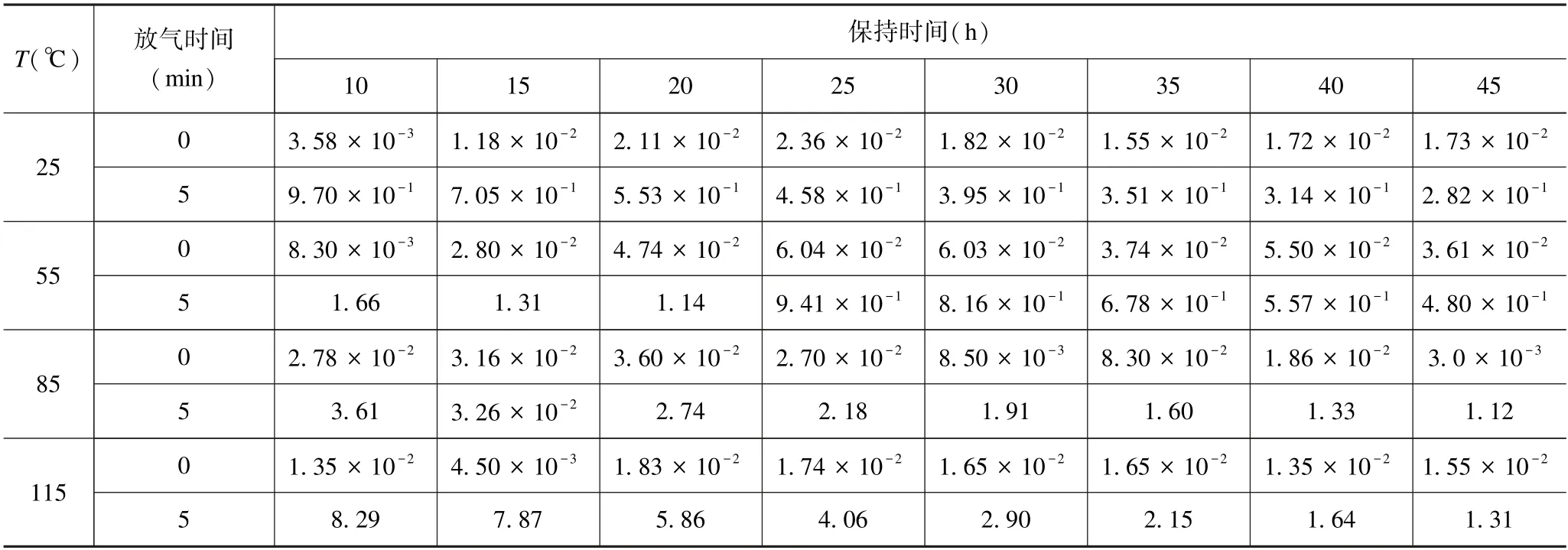
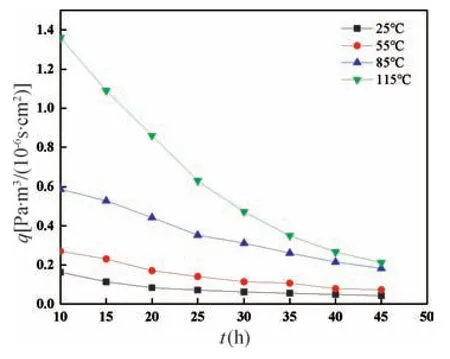
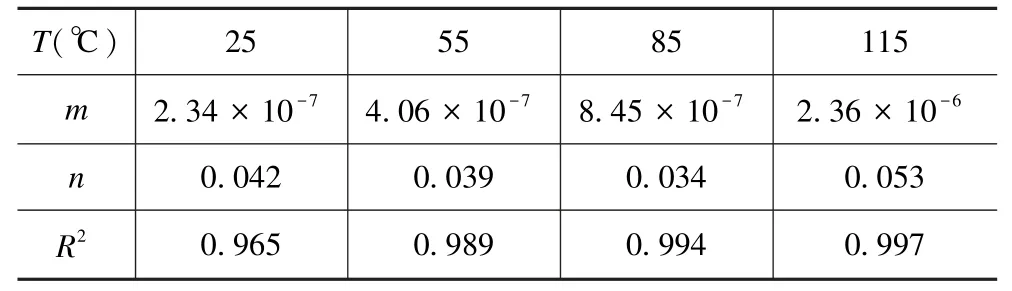
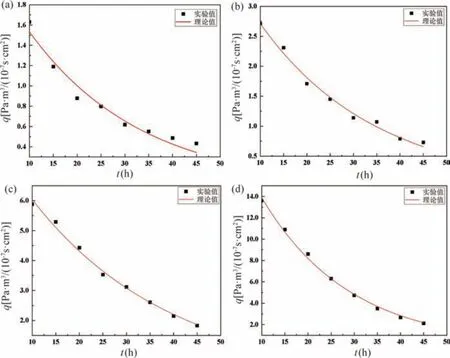
初始条件:C=C0,0

边界条件:C=0,x=d,t>0。

应用分离变量法[10]解得:

当环氧粘结材料的一面完全置于真空中时,从平板单位面积流出的瞬时气体流量为:

只有当n=0 时第一个指数项在长时间内计算才有意义,因此,方程(5)可以进一步写为:

其扩散系数D还受温度影响,与温度T呈指数关系[11],即:

式中:D0为比例常数;Ed为扩散激活能;R为通用气体常数;T为绝对温度。

结合(6)式和(7)式可知,扩散系数D随扩散激活能Ed的增大而减小,进而导致材料的释气速率q减小;但如果粘结材料的温度升高,扩散进行得越快,则材料的释气速率q越大,表明材料的释气速率受温度影响。

(6)式即为环氧粘结材料的释气速率随时间变化的关系表达式。式中参量包括初始气体浓度C0、材料厚度d、扩散系数D以及与D有关的一些常数等都和环氧粘结材料本身的性质有关。因为条件有限,有些参数不方便通过实验直接测得。因此,令m=n,可以方便后续的研究工作,则(6)式可以简化为:

根据(8)式,结合相关实验数据,对其进行曲线拟合,可以得到m、n的具体取值,进而建立起环氧粘结材料的释气速率随时间变化的数学理论模型。进一步对(8)式在t时间段内进行积分,可得环氧粘结材料在t时间段内的总释气量Q,即

2 实验分析与模型验证

一般情况下,真空腔的形成可以使用陶瓷和金属外壳将器件封装在一个小型真空环境中,采用硅-玻璃键合和硅-硅键合工艺来实现[12]。在键合过程中,为避免使用一些复杂的工艺,如制作过孔或抛光等,常用玻璃焊料的工艺来实现玻璃/硅、玻璃/玻璃的键合,如用低温玻璃焊料。MEMS 传感器的真空封装腔体剖面图如图2 所示。

图2 MEMS 传感器的真空封装腔体Fig.2 Vacuumized cavity of MEMS sensor

为了验证理论模型描述环氧粘结材料释气特性的适用性和准确性,借助文献中测得的实验数据,对实验数据进行曲线拟合,将拟合的结果与真实的实验数据对比并进行误差分析,可以得到具体参数的值,进而建立起完整的理论数学模型。实验基于静态升压法实验原理搭建环氧粘结材料的释气装置,主要由抽空单元、测试单元和数据采集单元组成。该实验针对的是具体的环氧粘结材料,根据实验中测试室的容积以及实际MEMS 器件的大小合理地假设了真空腔的体积V以及环氧粘结材料处于真空腔一侧的表面积S。实验过程中,材料在不同温度下保持一段时间后,首次测量真空度值,以及5 min 之后再次测量真空度值,二者的时间间隔称为放气周期,实验得到环氧粘结材料各个放气周期真空腔内真空度值变化规律见表1 所列。

表1 放气周期真空度值变化Tab.1 Change of vacuum degree during outgassing period

根据静态升压法[13]相关公式可知:

式中: Δt为释气时间;Δp为真空度值的变化量。

从表1 中实验数据可以计算得到不同温度下环氧粘结材料的释气速率,在数据分析与绘图软件MATLAB 中绘制出释气速率随时间的变化规律曲线,如图3 所示。

图3 不同温度下环氧粘结材料释气速率随时间的变化关系Fig.3 Variation of outgassing rate of epoxy bonding materials across time at different temperatures

从图3 可以看出,在一定温度下,环氧粘结材料的释气速率随时间逐渐变小;相同时间下,温度越高,释气速率衰减越快。随着温度升高,环氧粘结材料的释气速率呈现出指数衰减趋势。造成这一现象的主要原因有两方面[14]: (1)水汽不断释放的过程中,空腔内的水汽压力在逐渐增加,从而降低了释气速率;(2)可释放的水汽量在逐渐减少。综上所述,温度对释气速率的影响显著,释气速率随温度的升高衰减加快。

利用MATLAB 软件把不同温度下的实验数据代入(8)式中进行拟合处理,结果如图4 所示。拟合不同温度下环氧粘结材料的释气速率曲线得出相关系数R2以及m、n的值,见表2 所列。

表2 m、n 取值及拟合相关系数Tab.2 m and n values and fitting correlation coefficients

图4 不同温度下实验数据和拟合释气速率。(a)T=25 ℃;(b) T=55 ℃;(c) T=85 ℃;(d) T=115 ℃Fig.4 Experimental data and fitting outgassing rate at different temperatures.(a)T=25 ℃;(b) T=55 ℃;(c) T=85 ℃;(d) T=115 ℃

从图4 可以看出,图4(a)和(b)中曲线贴合度较低,从表2 可看出,在25 ℃和55 ℃下的拟合相关系数R2的值都较小,说明在这个温度范围内,真实的释气过程与理论模型存在较大差异。当温度为85 ℃和115 ℃时,图4(c)和(d)中曲线贴合度较高且表2 中拟合相关系数R2的值都更接近于1,误差较小,说明拟合效果在此温度范围内较好。综上所述,相关系数R2值随温度的升高在逐渐增大,说明二者的曲线贴合度变高,误差也在逐渐减小。在此温度范围内,建立描述真空封装内部环氧粘结材料的释气特性的理论模型较为准确。

通过上述分析,结合表2 可知,115 ℃时环氧粘结材料的释气速率随时间的变化关系为:

由于该模型使用的封装材料为环氧粘结材料,是在115 ℃下拟合所得,该结果具有一定的局限性,但总的研究思路是通过升高温度加快材料释气的进程,进而缩短实验时间,环氧粘结材料的释气总量不变,因此115 ℃时所建的理论模型接近真实的释气模型,MEMS 传感器环氧粘结材料的释气总量可以采用如下公式计算:

研究表明,环氧粘结材料释气的主要成分为水汽,封装内部水汽含量过高容易减少器件的使用寿命。按照GJB 548—2005 的规定,封装内部水汽含量要求不高于体积分数5000×10-6。将MEMS 传感器真空腔内水汽含量作为气密性的性能退化指标,在达到该阈值时器件失效,该理论模型的建立为MEMS 传感器的封装可靠性提供了理论依据。

根据公式(相对误差=| 真实值-理论值|/真实值)可以计算出相对误差[15]。通常在实验数据非常复杂的情况下,为了简化计算,转化为计算两个函数曲线之间的相对距离和真实值的比值来计算相对误差。

从图4 可以看出,图4(a)中的拟合结果与实验结果差距最大,因而只用针对该图中相差较大的第一组实验数据进行计算,通过MATLAB 图像处理软件可以准确地计算出对应的函数值,代入相对误差公式,结果如下:

研究基于模拟仿真的验证技术,对比验证退化机理模型的计算结果与模拟仿真结果之间相对误差<5%,达到了项目的精度要求,数据吻合较好,验证了模型的正确性。

3 结论

本文通过研究真空封装内部常用的环氧粘结材料的释气特性,考虑了不同温度对材料释气速率的影响,在菲克第二定律的基础上建立了真空腔中环氧粘结材料释气的理论数学模型,实验模型与理论模型能较好吻合,误差较小。结果表明,当温度不变时,环氧粘结材料的释气速率随时间不断减小;当温度升高时,释气速率随时间的变化呈指数衰减趋势。该理论模型的建立为后续对MEMS 传感器封装可靠性的分析提供了重要的理论基础。