基于SSA-VMD-GRU 的锂电池剩余寿命预测方法研究

2023-11-14丁德邻张营左洪福

电子元件与材料 2023年9期

丁德邻 ,张营, ,左洪福

(1.南京林业大学汽车与交通工程学院,江苏南京 210037;2.南京航空航天大学民航学院,江苏南京 210016)

锂离子电池因具有能量密度高、质量轻、循环寿命长等优点[1],在新能源汽车和储能等领域应用广泛。然而,在锂离子电池持续充放电过程中,由于其内部发生的不可逆电化学反应,会导致电池单体的内阻增大、容量减小,使电池单体的性能发生退化[2]。进而导致电池剩余使用寿命(Remaining Useful Life,RUL)的衰减[3]。准确检测出锂离子电池的RUL,不但可以大大提高锂离子电池的安全性和可靠性,而且还能够延续电池的使用寿命[4],减少相关损耗[5]。

为了跟踪电池的衰减过程,通常以容量为健康指标。一般来说,当电池容量到达额定值的70%时,就认为锂离子电池失效[6]。目前锂离子电池的RUL 预测方法可分为两类: 基于模型的方法和数据驱动的方法。由于数据驱动方法规避了因为电池内部结构、电化学反应等无法建模的复杂问题[7],因此成为当前的研究热点。数据驱动技术通过训练大量的数据,分析锂电池以往的失效数据或工作时健康因子的变化规律即可实现寿命预测,但也要求数据信息充足且相对稳定。目前基于数据驱动的方法有支持向量机[8]、神经网络[9]、高斯回归[10]、贝叶斯蒙特卡洛[11]、基于集成的系统[12]和隐马尔可夫模型[13]等。

然而,锂离子电池在退化过程中会出现松弛效应,松弛效应指容量再生现象,其表现为下一周期的容量高于前一周期,并且在接下来伴随着加速退化[14]。这导致预测的衰退曲线往往欠拟合。Liu 等[15]使用高斯过程回归模型捕捉到局部的容量再生,并将高斯过程回归与长短记忆网络(GPR-LSTM)结合完成提前一步或多步预测容量。刘家豪等[16]通过结合长短期记忆网络和电化学阻抗谱理论(LSTM-EIS)对衰减趋势进行了预测。杨彦茹等[17]提出了一种支持向量回归(SVR)模型的预测方法,该方法通过完全集成经验模式分解(CEEMDAN)分解原始数据,再对分解后的数据进行预测,更好地捕捉了容量再生。Yang 等[18]提出了一种混合模型来预测RUL,该模型将集成经验模式分解(EEMD)、灰狼优化和支持向量回归(GWO-SVR)相结合,这种分解信号再进行预测的方法一定程度上提高了模型精度,启发更多研究人员选择信号分解与神经网络结合的方法来实现健康诊断和故障预测。

通过信号分解例如经验模态分解(EMD)能够将复杂的电池容量序列数据分解为一系列的模态分量(IMF)。然而,在分解高度复杂的序列时仍然存在分解不足和过度的问题。为了解决这一问题,后来有学者提出了变分模态分解(VMD)方法,该方法具有良好的理论基础和噪声鲁棒性。但是,在VMD 分解过程中,分解层数K和惩罚因子α是决定VMD 分解是否能产生良好结果的两个重要参数。王冉等[19]提出了一种基于VMD 和集成深度模型的锂电池RUL 预测方法,利用多层感知器和LSTM 对整体退化趋势和各种波动分量进行建模,并手动设置了VMD 参数。手动设置参数往往依赖人工经验,难以具有自适应性。作为经典的智能算法之一,麻雀搜索算法(SSA)可以自适应选择最优参数,使得算法更加简单高效。此外,门控循环单元(GRU)因具有结构简单和计算效率高等优点,被广泛应用于诊断和预测领域。它在提取复杂的时间序列和提高预测模型的精度方面具有突出的优势。

综上所述,针对容量再生以及信号复杂问题,本文以容量为健康指标,结合SSA 与VMD 自适应获取最优参数,提高分解效率,降低原始信号的非光滑性、非线性和复杂性。同时以GRU 捕捉层序变化过程中的微小变化,预测信号变化趋势,并测试了三种预测模型的精度,基于阈值测算RUL,在NASA 公共数据集上验证模型的有效性。

1 基本理论

1.1 VMD

变分模态分解(VMD)是一种自适应拆解技术,它可以将输入信号分解为K个调频调幅子信号(即模态分量IMF),每个模态分量有不同中心频率的有限带宽,具有良好的噪声鲁棒性。基本思想是将信号分解过程转化为约束变分问题,步骤如下:

(1) 构建函数。建立约束模型是为了获得IMF 分量估计带宽之和的最小值,约束模型为式(1):

式中:K是模态分解个数;∂t表示求偏导;σ(t)是狄拉克分布;y(t)是原始的数据信号;uk(t)是y(t)的模态分量;ωk表示中心频率;∗代表卷积。

(2) 解决变分问题。通过引入二次惩罚因子α和拉格朗日乘法因子θ(t),使得变分问题无约束性。拉格朗日表达式如式(2)所示。

式中:{uk}和{ωk}表示uk和ωk的集合;〈·,·〉表示函数内积算子。

使用交替方向乘子法(ADMM)优化和更新uk和ωk,以找到约束变分模型的最优解,具体表示为式(3):

设置判别精度δ(δ>0),达到条件式(4)停止收敛:

计算y(t)和各分量IMFk(t)之间的相关系数rk,可得分解信号与原信号的相关度,rk可表示为式(5):

其中VMD 参数K与α,本文通过寻优算法自适应获取。

1.2 SSA

麻雀搜索算法(SSA)是一种较为新颖的优化算法,主要思想是通过模仿麻雀的觅食和反捕食行为来进行局部和全局搜索[20]。在麻雀种群中,存在两种行为模式: 发现者和跟随者。发现者主动寻找丰富的食物来源,并提供觅食方向和区域,跟随者通过发现者获得食物[21]。在每次迭代期间,发现者和跟随者的位置用式(6)和式(7)更新:

式中:t是当前迭代次数;表示第i个麻雀在第t次迭代时的第j维位置;T是最大迭代次数;α∈[0,1]是一个随机数;Q是服从标准正态分布的随机数;L表示元素均为1 的1×d矩阵;R2∈[0,1]和ST∈[0.5,1]分别表示预警值和安全值;Xp表示麻雀的最佳位置;Xw表示全局最差位置;A表示1×d维矩阵,每个元素随机分配为1 或-1,且A=AT(AAT)-1。

用于侦察警告的麻雀通常占总数量的10%～20%,位置更新如式(8):

式中:β是步长控制参数;K∈[-1,1]是正态分布随机数,指示麻雀移动方向以及步长;fi表示第i个麻雀的自适应值;fg和fw分别表示当前全局最佳和最差适应值;ε表示常数,避免分母为零。

1.3 SSA-VMD

利用SSA 算法优化VMD 的参数(K和α)。K的取值决定了分解IMF 分量的个数。如果K值太大,会导致分解过度,产生一些无效的假分量。如果K值太小,则不能充分分解原始信号,而α的大小会影响分量信号的变化趋势,因此需要确定最优组合[K,α]来实现对信号的VMD 充分分解。

本文采用SSA 算法对VMD 参数进行优化,选取模型的均方误差(MSE)作为目标函数。计算公式如式(9)所示。

式中:ym表示目标函数;n为采样点数;yt表示真实值;yti表示预测值。

使用SSA 优化VMD 参数的流程如下:

(1)SSA 初始化参数,包括种群大小、迭代次数。设置K参数范围[1,8],设置α参数范围[1,2000],避免设置范围过小,导致模态分量中的特征信息较少。

(2)利用VMD 对锂离子电池的容量信号进行分解,得到多个IMF 分量。

(3)计算每个[K,α]对应位置的目标函数值,更新最佳目标函数值。

(4)确定迭代是否完成。输出最佳[K,α]组合,否则,继续迭代。

1.4 GRU

门控循环单元(GRU)作为另一种基于门的循环神经网络,其结构更小,性能与LSTM 单元相当。GRU由两个门组成: 重置和更新。GRU 的结构如图1 所示。rt和zt分别表示重置门和更新门。计算公式如式(10)所示。

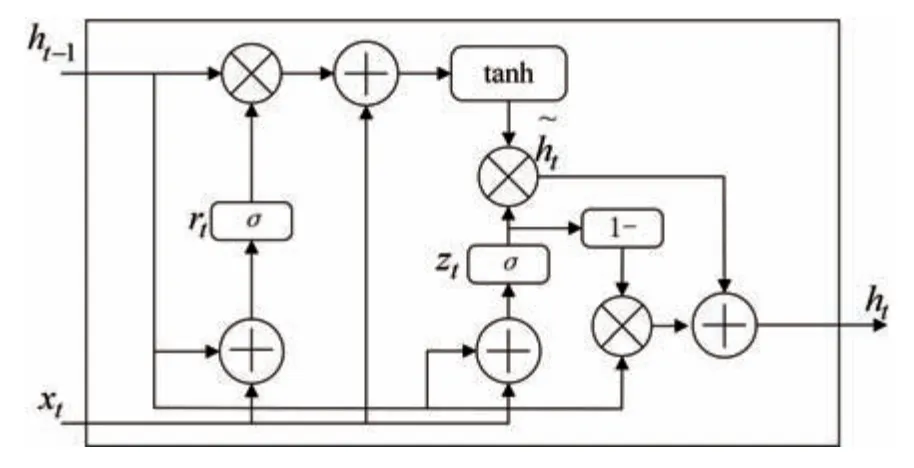
图1 GRU 结构Fig.1 Structure of GRU

式中:xt为t时刻的输入信息;ht-1是(t-1)时刻的隐藏状态;W和U是对应的权重矩阵;b是偏置矩阵;σ表示sigmoid 函数,它将得到的激活结果变换到0 与1之间;☉表示点积;表示t时刻候选隐藏状态;ht为t时刻的输出状态。

与RNN 和LSTM 类似,GRU 使用其先前的时间步长输出和当前输入来计算下一个输出。GRU 由于具有更低的内存需求、更少的可训练参数和更低的训练时间,因此性能更为优异。

1.5 基于SSA-VMD-GRU 方法的实现

本文结合SSA、VMD 与GRU 方法,整体流程如图2,主要步骤如下。

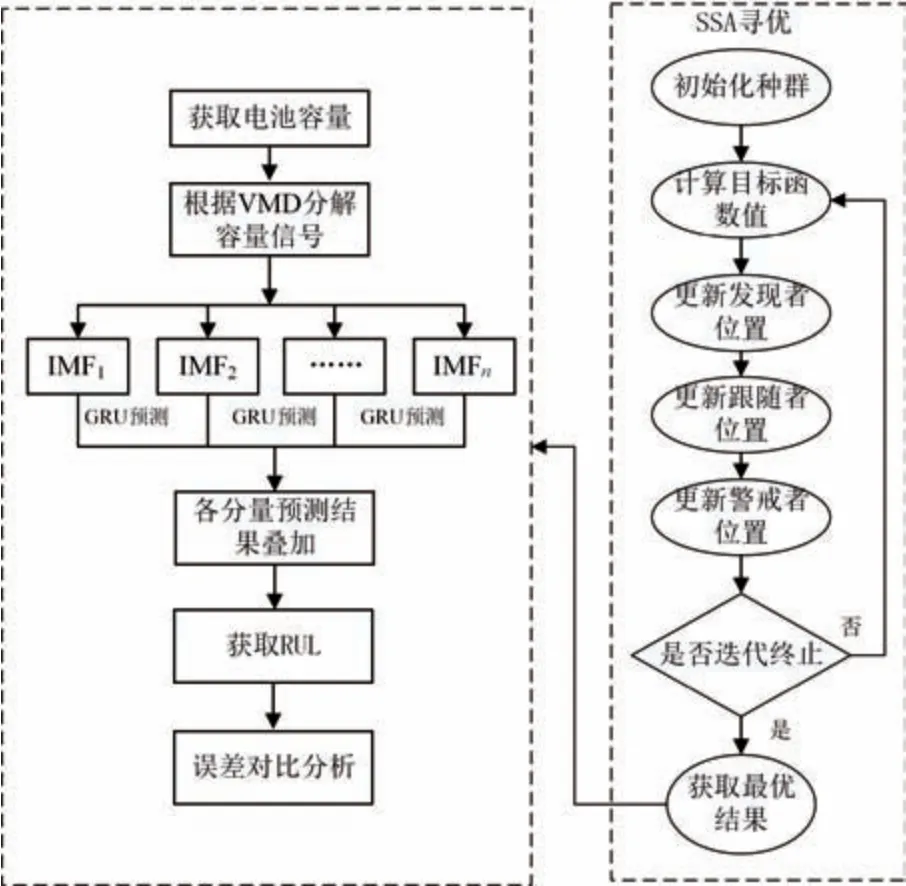
图2 预测流程Fig.2 Prediction flowchart

(1) 获取电池性能衰退数据,提取容量C,记为C1,C2,…,Cn。其中,Ci表示第i个周期所对应的容量值,i=1,2,…,n(n表示总的循环数)。

(2) 利用VMD 对数据进行分解,同时采用SSA对关键参数K与α进行寻优,目标函数为均方误差(MSE) 最小值。最终分解得到各模态分量IMF1,IMF2,…,IMFn。

(3) 基于分解的各个分量分别构建模型预测,分别划分训练集与测试集,训练集记为{x,y},测试集记为{xt,yt},将训练集{x,y}代入模型,xt作为模型的输入,输出yti。

(4) 将各个预测结果叠加,即可得到最终预测结果。获取电池RUL,通过误差指标评估精度。

1.6 评价指标

为了评估该方法的预测性能,使用均方根误差(Root Mean Square Error,ERMS)和平均绝对百分比误差(Mean Absolute Percentage Error,EMAP)评估模型容量预测精度,使用绝对误差(Absolute Error,EA)评估RUL 预测精度,评价指标分别如式(11)、式(12)和式(13)所示:

式中:R表示RUL 真实值;Rp表示RUL 预测值。若评价指标值越小,则精度越高。

2 实验分析

2.1 数据

本文中的实验数据来自美国宇航局发布的电池数据集。通过在室温下对锂离子电池进行充放电来测量容量退化数据。当电池容量低于阈值时,可以判断电池功能失效。由于电池容量下降到额定值的70%时可以认定为失效,故本次实验的电池容量失效阈值定为1.3 A·h。本文以B5 与B6 电池为例,对所提出的方法进行了分析和验证。电池容量衰减曲线如图3 所示。随着循环周期的增加,电池的总容量呈下降趋势,但由于某些循环中的容量再生现象,曲线略有反弹。

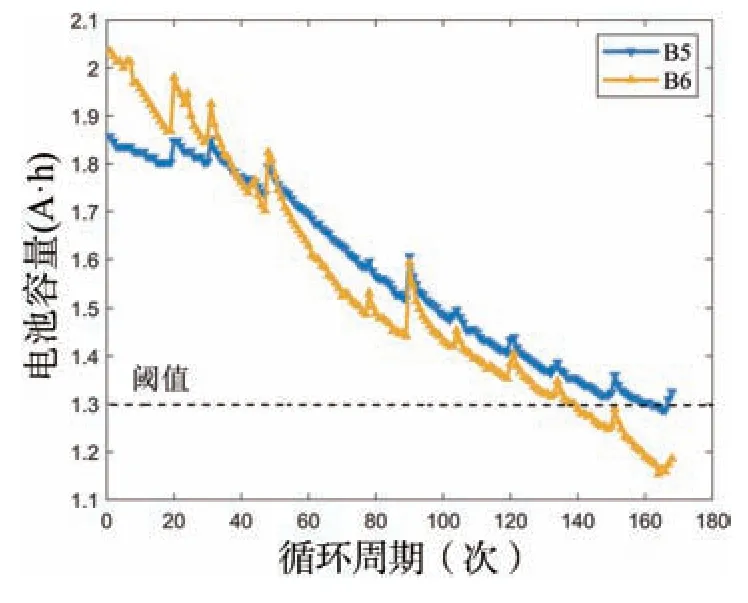
图3 电池容量衰减Fig.3 Capacity degradation of battery

2.2 VMD 信号分解

经SSA 优化后输出B5、B6 电池的最佳VMD 参数组合如表1 所示。

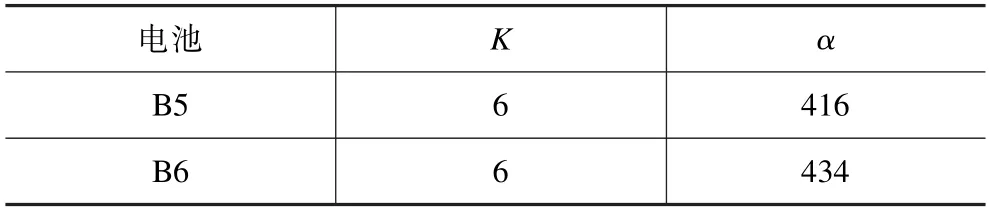
表1 参数组合Tab.1 Parameter combination

已知VMD 最优参数组合,B5 和B6 分解如图4所示,其分量与原信号的相关系数如表2 所示,为了验证K和α对分解效果的影响,以B5 为例再将K设置为6,α设置为1000 和K设置为3,α设置为416 与EMD 分解效果及最优分解效果作对比,效果如图5 所示。由表2 可以看出,锂电池B5 和B6 中IMF6 的相关系数最高,说明与原始信号相关,且其容量退化趋势也与原信号相近。而其他各IMF 均较低,则视为与原始信号弱相关,是由于电池劣化以及容量再生等干扰带来的不规则分量。这也进一步证明了电池衰退的过程是非线性和非平稳的,通过信号分解可以有效降低信号复杂度。

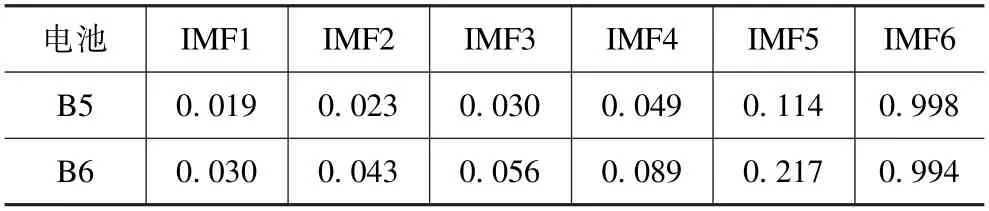
表2 两组电池分量和原始信号之间的相关系数Tab.2 Correlation coefficient between two sets of battery components and the original signal

图4 两组电池容量信号分解图Fig.4 Decomposition diagram of two battery capacity signals

图5 三种分解方式效果图Fig.5 Three decomposition methods renderings

相比于自适应选择参数,图5(a)中的IMF5 和IMF6 可以观察到,α的大小会影响分量信号的变化趋势,使得对衰退趋势的捕捉受到影响。结合图5(b)与图4 可以看到,分解个数K对分解结果产生直接影响,由于K值设置过小导致目标曲线欠分解,无法降低曲线的复杂程度,这种情况下,预测模型可能无法提供更高的预测精度,K与α均会最终决定预测结果的准确率,而图5(c)的EMD 分解则存在模态混叠现象,特征信息不明显。本文所采用的方法充分分解了锂离子电池信号,能够更好地表达全局衰退趋势特征,并且不需要再手动设置参数,摆脱了经验依赖。

2.3 预测结果

为了验证实验的有效性,分别以原数据的30%,50%和70%用作训练集训练模型,然后将剩余的数据用作测试模型,同时与EMD-GRU 模型和单一LSTM模型进行比较。

将已分解的分量的训练集数据作为模型的输入进行预测,再将分量预测结果进行融合得到最终的电池容量结果如图6 所示。

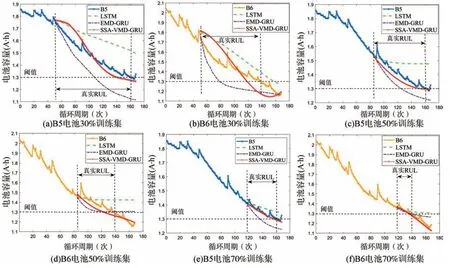
图6 三种训练集比例的预测结果Fig.6 Prediction results of three training set proportions

三种方法容量预测的误差以及RUL 的误差统计如表3 所示,部分预测曲线未到失效阈值,故以“-”表示。

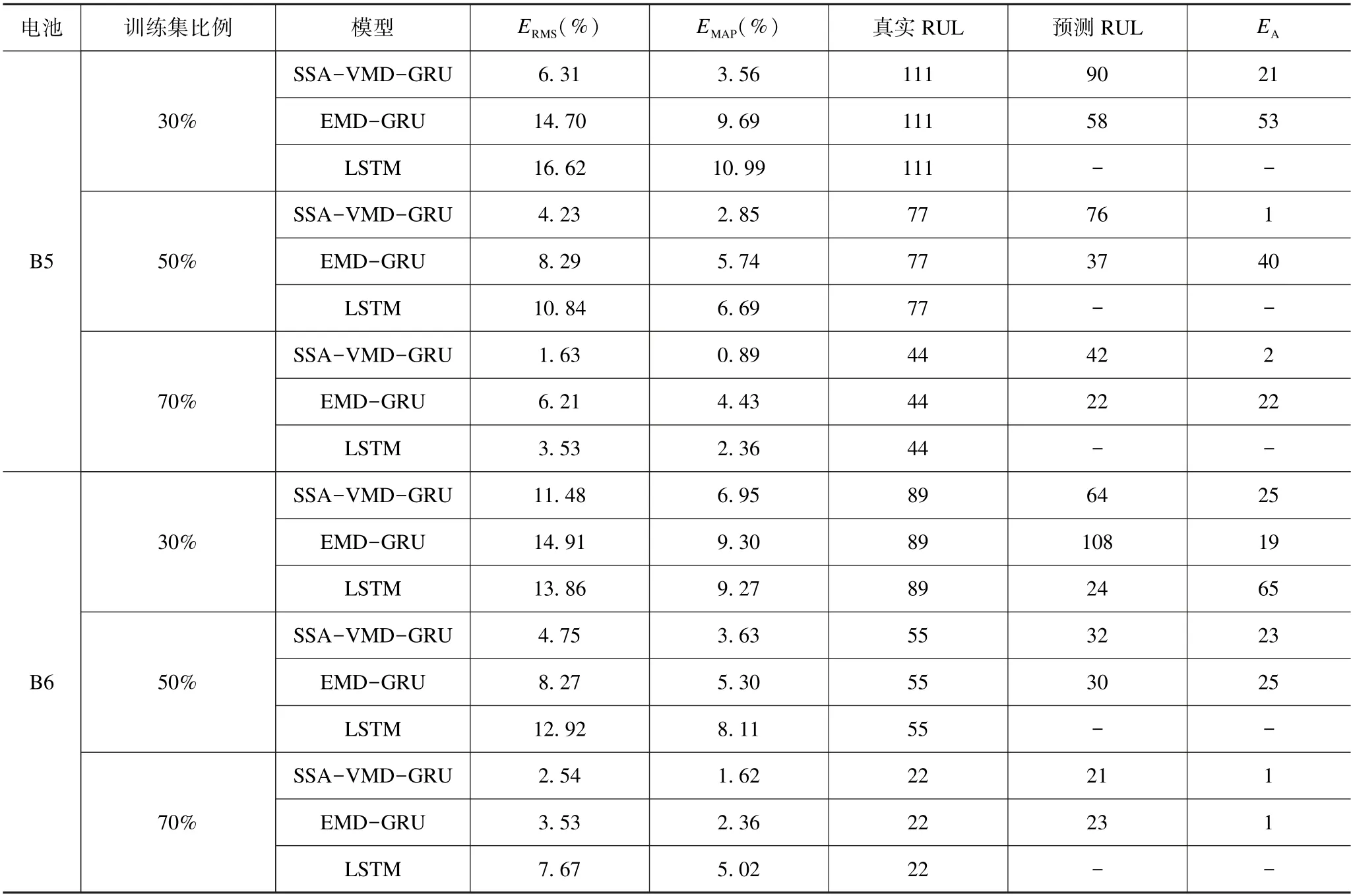
表3 三种方法不同训练集比例下的预测误差与RUL 预测误差Tab.3 Prediction error and RUL prediction error under different training set ratios of three methods

综合比较预测结果和评价指标,总结如下:

(1)从图6 和表3 可以看出,本文方法的预测结果明显优于LSTM 和EMD-GRU。当B5 电池以30%比例训练模型时,本文方法相比于EMD-GRU 与LSTM分别提升了57%与61%,以50%比例训练模型时分别提升了50%与60%,以70%比例训练模型时分别提升了73%与54%,这两种方法可以在一定程度上反映容量的退化趋势,然而随着循环周期的增加,误差也变大,而SSA-VMD-GRU 能够更好地追踪容量的变化,并且在不同电池、不同起点下的预测曲线更能反映电池信号的衰退,预测较为稳定。在RUL 预测方面,本文提出的SSA-VMD-GRU 方法预测结果的误差更小,预测精度较高,相比于另两种方法均提升50%以上。组合模型的预测能更好地抓住容量的走势,这表明通过对容量进行优化分解,建立预测模型,能更好地预测高度非线性和非平稳的数据,为获取RUL 提供至关重要的信息。

(2)从表3 不同训练集比例的结果来看,训练集的数量直接影响了预测模型的精度,训练数据越多,预测精度越高。当训练集样本较少时,可以看到模型误差明显增大,RUL 预测更加困难,训练集样本越多,模型精度越高,预测曲线越贴合原信号走势,RUL 预测也越准确。

(3)从图6 和表3 可以看出,组合模型EMD-GRU相比于LSTM,由于EMD 对容量信号进行了分解,降低了容量再生的影响,使得其效果相对好于LSTM 模型,但仍低于本文所用方法。进一步分析由于VMD方法避免了EMD 的模态混叠的影响,并且经过超参数的优化,较好地降低了信号的复杂性,使得分解效果更加优异,因而预测效果显著提高。故本文方法在预测精度上具有明显的优势。