混合时间窗下多中心混合车队车辆路径优化
2023-11-14范厚明张跃光孙秀娜田攀俊
范厚明, 杨 成, 张跃光, 孙秀娜, 田攀俊
(大连海事大学 交通运输工程学院,辽宁 大连 116026)
0 引言
混合时间窗下多中心混合车队车辆路径问题(Multi-Depot Mixed Fleet Vehicle Routing Problem with Mixed Time Windows, MDMFVRP-MTW)是在多中心联合配送模式下,考虑客户对服务时间的要求及完成配送任务后各配送中心的运力平衡程度不同,对多型电动车和燃油车组成的混合车队配送路径进行优化的车辆路径拓展问题。现实中,京东、菜鸟等物流企业均通过共享配送区域内多个配送中心的资源进行联合配送,以降低成本、提高效率,更好地满足客户多样化服务的需求。同时,与传统燃油车相比,电动车在环保、运营成本等方面具有显著优势,许多物流企业都开启了使用电动物流车取代燃油车的进程,出现了物流企业同时采用电动车和燃油车进行配送服务的情况,如亚马逊、京东。另外,美团、京东等企业根据客户是否购买准时送达服务,将客户区分为硬时间窗客户和软时间窗客户,实际物流服务中客户为混合时间窗的情况大量存在。MDMFVRP-MTW能更准确地描述部分配送模式,例如拥有多个配送中心且各中心配置有多种车型电动车和燃油车的物流企业对区域内的顾客进行联合配送,通过合理规划配送车辆类型、服务顺序等,在客户不同类型的时间窗内完成配送服务。因此,针对MDMFVRP-MTW的研究具有重要意义。
带混合时间窗的车辆路径问题(Vehicle Routing Problem with Mixed Time Windows, VRPMTW)是从带时间窗车辆路径问题(Vehicle Routing Problem with Time windows, VRPTW)衍生出的更为复杂的问题。已有学者对VRPTW的各类衍生问题进行了研究。ONGCUNARUK等[1]考虑城市配送中的城区限制,即要求在统一硬时间窗内完成部分区域内客户的需求,以车辆固定成本、可变成本之和最小为目标建立优化模型,并设计改进的遗传算法进行求解;TAS等[2]针对一种特殊的时间窗形式,即允许车辆在其时间窗外一定范围内到达,但需要支付一定的惩罚成本,以车辆可变成本、固定成本和时间窗惩罚成本之和最小为目标建立VRPTW优化模型,并设计改进的禁忌搜索算法进行求解;范厚明等[3]针对客户的模糊需求和模糊时间窗,以总行驶距离最小化、平均客户满意度最大和车辆使用数量最小为目标建立VRP优化模型,并设计混合遗传算法进行求解。本文VRPMTW同时存在软时间窗约束客户和硬时间窗约束客户,目前相关研究较少。周蓉等[4]针对因客户订单时间紧迫程度不同而使软硬时间窗共存的情况,如紧急订单与常规订单可分别视为硬时间窗约束和软时间窗约束,以总成本最小为目标建立同时集送货VRP优化模型,并设计改进离散粒子群算法进行求解;FALLAHTAFTI等[5]针对第三方物流配送中同时存在带硬时间窗的供应商与带半软时间窗的工厂和仓库的现实特征,以总成本最小为目标建立VRPMTW优化模型,并设计分支定界算法进行求解;王勇等[6]提出将客户重要度与时间窗相结合的差异化管理策略,该策略首先对客户重要度进行评价,其次对重要客户进行硬时间窗管理,对普通客户进行软时间窗管理,以成本最小和配送车辆数最小为目标建立双目标优化模型,并设计遗传—禁忌搜索混合算法进行求解;邹宗峰等[7]考虑危险品运输网络中同时具有软硬时间窗限制,以运输风险、时间窗惩罚成本、交通状况、道路能力、运输时间最优为目标,建立带混合时间窗的多目标路径优化模型,并设计改进的多目标遗传算法进行求解。
本文涉及的MDMFVRP既是多中心异型车辆路径问题(Multi-Depot Heterogeneous fleet Vehicle Routing Problem, MDHVRP),也是燃油车与电动车构成的混合车队路径优化问题。针对MDHVRP,马建华等[8]针对车辆在应急状态下进行配送,配送结束返回原配送中心,以总配送时长最小为目标建立MDHVRP优化模型,并设计变异蚁群算法进行求解;张群等[9]针对多货种配送,车辆配送结束返回原车场,以总行驶距离最小为目标建立多货种MDHVRP优化模型,并设计改进模糊遗传算法进行求解;罗鸿斌[10]同样考虑车辆配送完成返回原配送中心,以车辆运输成本最小为目标建立MDHVRP优化模型,并设计改进的粒子群优化算法进行求解。在电动车车辆路径问题(Electric Vehicle Routing Problem, EVRP)研究中,SCHNEIDER等[11]针对带时间窗和充电站的EVRP问题,以行驶距离最小为目标建立电动车路径优化模型,并设计一种结合可变邻域搜索算法和禁忌搜索算法的混合算法进行求解;HIERMANN等[12]考虑异型电动车的运输能力、电池尺寸和购置成本差异,以派遣成本和路径可变成本之和最小为目标建立带时间窗的路径优化模型,并设计自适应大邻域搜索(Large Neighborhood Search,LNS)算法进行求解;BASSO等[13]考虑地形、速度等因素对电动车能耗的影响,以能耗最小为目标建立EVRP优化模型,并使用Bellman-Ford算法进行求解;RAEESI等[14]使用移动换电车为电量不足的电动车提供换电服务,以总成本最小为目标建立了带时间窗的EVRP数学模型,并提出一种基于动态规划和整数规划的两阶段混合算法进行求解;KESKIN等[15]考虑充电站内充电桩的数量限制,以总成本最小为目标建立电动车排队等待服从M/G/1分布且考虑充电效率非线性的路径优化模型,并设计改进的自适应LNS算法进行求解。随着研究的深入,考虑同时使用电动车、燃油车进行配送的VRP研究逐渐丰富,李英等[16]针对MFVRP,以总成本最小为目标建立混合车队路径优化模型,并设计分散搜索和改进蚁群算法相结合的混合启发式算法进行求解;MACRINA等[17]考虑各充电站充电速度存在差异,以总成本最小为目标建立电动车不完全充电下的混合车队路径优化模型,并设计混合邻域搜索算法进行求解;SASSI等[18]在充电成本受时间变化的影响下,以总成本最小为目标建立具有时间依赖性的混合车队车辆路径优化模型,并设计包含多种插入策略的局部搜索算法进行求解;GOEKE等[19]考虑速度、坡度和载重量对能耗的影响,分别以行驶距离最小、充电成本与人工成本之和最小、电池更换成本最小为目标,建立非线性能耗的混合车队路径模型,并设计自适应LNS算法进行求解;LEBEAU等[20]考虑客户时间窗约束,以总成本最小为目标建立混合车队车辆路径优化模型,并设计节约试探法进行求解;MACRINA等[21]考虑电动车电池不完全充电策略和客户的硬时间窗约束,以总成本最小为目标建立MFVRP优化模型,并设计改进局部搜索算法进行求解。
通过梳理以上文献可知,现有研究已经取得一定成果,对本文研究具有重要指导意义,但还存在以下不足:①现有VRPTW的研究多考虑单一硬时间窗或软时间窗,缺乏对不同类型时间窗并存的车辆路径问题的研究;②现有MDHVRP研究中,各配送中心采取联合配送模式,但车辆返回策略均为返回原中心,该策略返回方案固定,其返回成本较高;③现有MFVRP研究的燃油车和电动车多为单一车型,缺乏对多车型燃油车或电动车并存的车辆路径问题进行研究。针对以上不足,本文MDMFVRP-MTW综合考虑影响油耗的多种因素和客户混合时间窗等约束,基于配送中心运力平衡的车辆返回策略,以车辆派遣成本、油耗成本、电动车能耗成本和时间窗惩罚成本之和最小为目标建立数学模型,并设计遗传—大邻域混合算法(Hybrid Genetic Algorithm with Large Neighborhood Search, HGALNS)进行求解。
1 问题分析与返回策略设计
1.1 问题描述
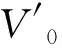
以图1为例,配送区域内有2个配送中心、12个软时间窗客户和12个硬时间窗客户,3种不同车型的车辆分别由配送中心1,2出发,并在时间窗约束下为客户提供配送服务,电动车2,3,5,6分别在服务客户5,10,19,22后由于电池最低荷电状态约束无法继续服务其他客户,就近选择存有该车型备用电池的配送中心更换电池,然后继续服务后续客户,车辆完成配送后遵循运力平衡原则选择配送中心返回。
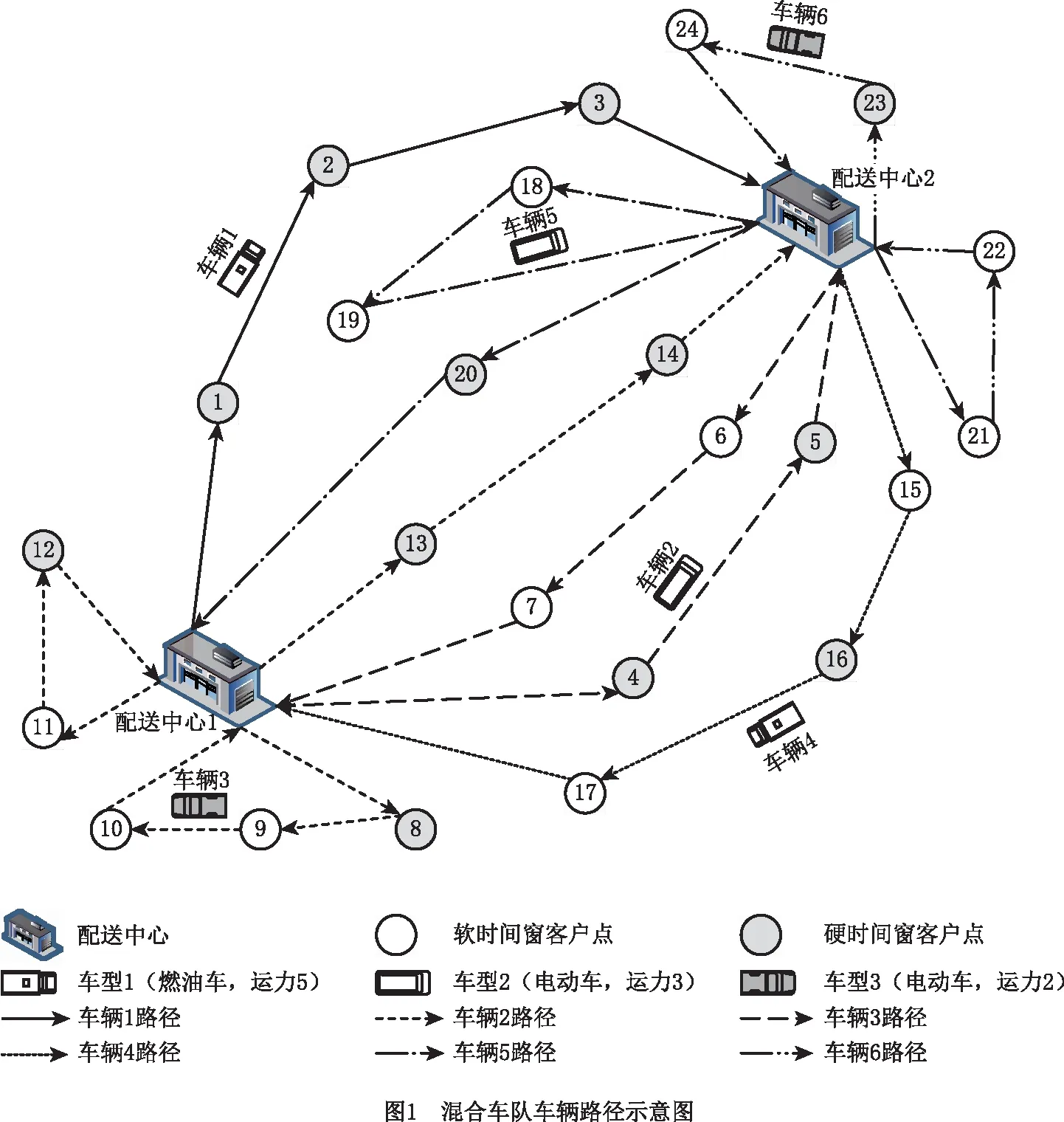
1.2 油耗成本计算
车辆行驶过程中的油耗与载重量等因素有关,本文采用文献[22]的综合模式排放模型(Comprehensive Modal Emission Model, CMEM)计算车辆油耗,该模型在已知车辆参数和行驶状态下,能够较准确地估计配送过程中车辆的燃油消耗量。根据CMEM模型可知,车辆由节点i到j的油耗率fij(单位:g/s)为
fij=φ(λNVs+Pij/η)/μ。
(1)
式中:φ为油气质量比;λ为发动机摩擦系数;N为发动机转速(单位:r/s);Vs为发动机排量(单位:L);η为柴油发动机的效率参数;μ为柴油的热量值(单位:kJ/g);Pij为车辆由节点i行驶至节点j所需的牵引功率(单位:kW),
(2)
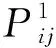
本文假设车辆为匀速行驶,道路坡度为0,则
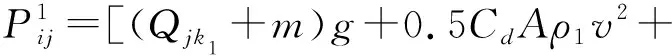
(3)
式中:m为车辆自重(单位:t);g为重力加速度(单位:g/m2);Cd为空气阻力系数;A为车辆迎风面积(单位:m2);ρ1为空气密度(单位:kg/m3);Cr为滚动阻力系数。
综合上述分析可得车辆k1从i到j的油耗Fijk1(单位:L)为
Fijk1=3.6fijlij/(ρ2·v)。
(4)
式中:ρ2为柴油密度(单位:g/mL);3.6为单位转换系数。
1.3 返回策略设计
目前MDHVRP研究中,车辆的返回策略为返回原配送中心。为保证各配送中心运力守衡,配送中心也可按照发出和接收的各车型车辆数守恒原则优化决策配送方案,这两种返回策略示意图如图2a和图2b所示。
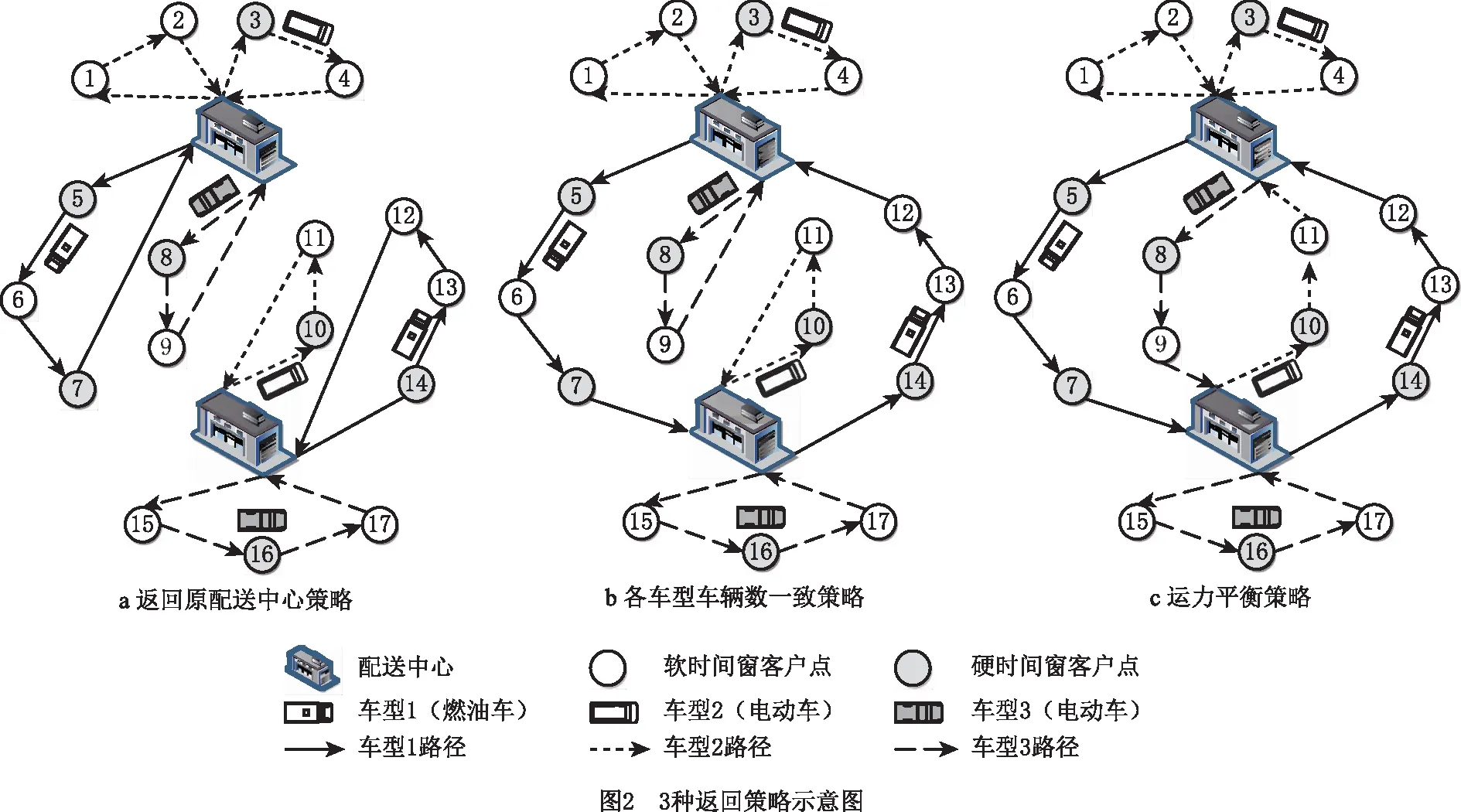
图2a为返回原配送中心策略,即各车辆完成配送任务后分别返回出发时的配送中心,该策略虽然能够保证各中心运力绝对平衡,但是车辆返回方案固定,车辆调度不灵活,运营成本较高。该返回策略的约束为
∀i∈V0,∀r∈R,∀kr∈Kr。
(5)
图2b为各车型车辆数平衡策略,即各车辆配送完成后可选择任一配送中心返回,但需要保证各中心各车型车辆数与初始状态相同。该策略通过多中心联合调度保证各中心运力绝对平衡,相比返回原中心策略,可选择的返回方案较多,但可能存在部分车辆返回较远的配送中心而造成较高运营成本的情况。该返回策略的约束为
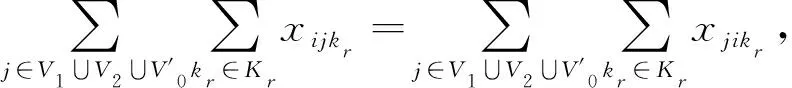
(6)
由上述分析可知,返回原配送中心策略与各车型车辆数平衡策略均存在可选择的返回方案较少、运营成本较高的缺点,而且在联合配送模式下,各配送中心客户与载具资源共享,配送中心无需维持车辆配置相同。因此,本文结合现实中配送中心每日配送任务量保持相对稳定但呈现小幅度上下波动的现状,提出运力平衡的车辆返回策略,该策略既能通过维持配送中心运力相对平衡保证配送中心的稳定运力供给,又能增加可选择的返回方案数量、降低运营成本。运力平衡的车辆返回策略要求车辆完成配送后根据各中心运力情况选择配送中心返回,允许各配送中心所有车辆的最大载重量之和在一定范围内浮动,但不得高于运力上限或低于运力下限。如图1中,各配送中心在配送前的总运力均为10,假设配送周期(1天)内运力允许的波动幅度为10%,车辆3若返回原配送中心1,则配送结束后配送中心1,2的总运力分别为13,7,均超出运力可接受的波动幅度,因此车辆3遵循运力平衡返回原则返回运力不足的配送中心2,此时配送中心1,2的总运力分别为11,9,均达到可接受的运力要求,而且避免了较长的车辆行驶里程。图2c为运力平衡的返回策略示意图,相比返回原配送中心策略和各车型车辆数平衡策略,该策略下车辆可选择的返回方案更多、车辆调度更灵活,既可降低运营成本,又能保证配送中心的基本调度需求。该返回策略的约束为
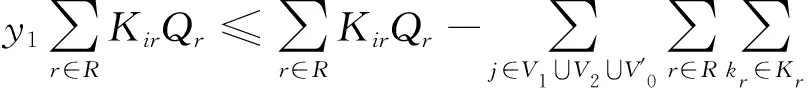
(7)
式中y1,y2分别为各配送中心的运力下限和运力上限系数。
1.4 目标函数
梳理近年来的文献可知,现有车辆路径问题大多以成本最小为优化目标。本文将以车辆派遣成本、油耗成本、电动车能耗成本和时间窗惩罚成本之和最小为目标建立数学模型。
派遣成本C1与车辆使用数量呈线性关系,不同车型派遣成本不同:
(8)
油耗成本C2的计算采用CMEM模型,由1.2节可知
(9)
由于缺乏准确的电动车能耗计算模型,电动车能耗成本C3和大部分EVRP文献相同,假设与车辆行驶距离呈线性关系,则有
(10)
时间窗惩罚成本C4包括硬时间窗早到等待成本、软时间窗早到惩罚成本和软时间窗晚到惩罚成本3项,其中不同车型因早到等待产生的硬时间窗机会损失成本不同,有
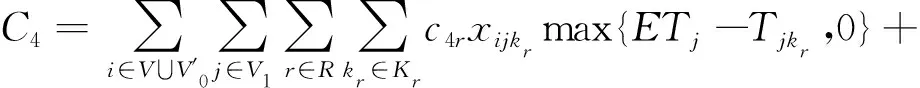
(11)
2 模型建立
基于以上分析,建立如下MDMFVRP-MTW数学模型:
目标函数
minC1+C2+C3+C4。
(12)
约束条件中,本文提出的运力平衡返回约束式(7)是其中的一个约束条件,除此之外,其他约束如下:
∀r∈R,∀kr∈Kr;
(13)
(14)
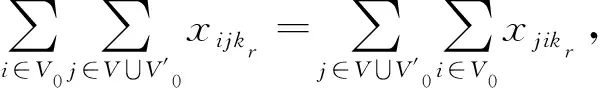
(15)
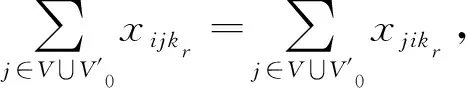
(16)
(17)
∀i∈V1,∀r∈R,∀kr∈Kr;
(18)
Ts≤Tikr≤Tf,
∀i∈V0,∀r∈R,∀kr∈Kr;
(19)
(20)
(21)
(22)
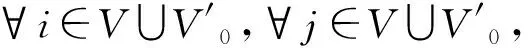
(23)
(24)
Qik1-di-M(1-xijkr)≤Qjk1,
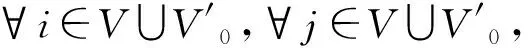
(25)
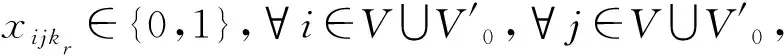
(26)
其中:式(12)为目标函数,即以车辆派遣成本、油耗成本、电动车能耗成本和时间窗惩罚成本之和最小为目标;式(13)表示车辆服务客户的需求量之和不超过其最大载重量;式(14)表示每个客户点只被服务一次;式(15)表示车辆由配送中心出发,最终返回任一配送中心;式(16)表示客户与换电节点车辆进出平衡;式(17)表示r型电动车到配送中心j的换电次数不超过该配送中心配备的r型电动车电池的数量;式(18)表示车辆在硬时间窗客户点可接受的时间窗内为其提供服务;式(19)表示车辆必须在配送中心工作时间窗内执行配送任务;式(20)表示车辆由节点i出发到达节点j的时刻,同时消除子回路;式(21)约束配送中心i派出的r型车车辆数不超过其拥有的最大车辆数;式(22)表示车辆离开配送中心和客户点时的电量;式(23)表示配送过程中从i点出发的电动车到达j点时的电量;式(24)为电动车最低荷电状态约束;式(25)为从i点出发的车辆到达j点时的载重量;式(26)为决策变量属性。
3 算法设计
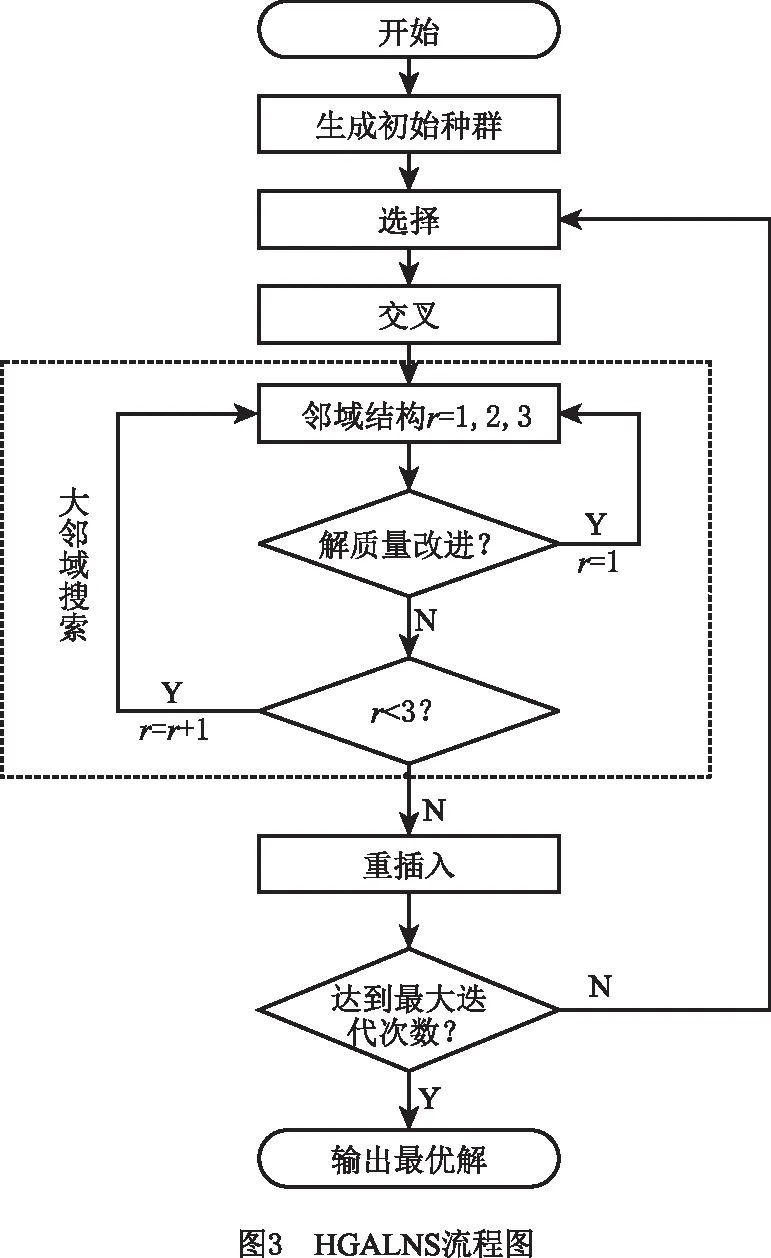
本文MDMFVRP-MTW是车辆路径拓展问题,包括多中心、多车型、混合车队、混合时间窗、电动车荷电状态约束、电池分布及数量约束、运力平衡返回规则等多个特征,属于NP-Hard问题,在该类问题求解中,精确算法求解较为困难。遗传算法(Genetic Algorithm, GA)是基于生物进化论中“适者生存”思想设计的经典启发式算法,具有较好的鲁棒性,适合求解复杂的优化问题,但在迭代后期易陷入局部最优,全局搜索能力较差;LNS通过对当前解决方案的重复“破坏”和“修复”寻找新的可行解,算法寻优能力强。因此,本文在GA基础上,将其与LNS算法结合。为了进一步提高算法的全局寻优能力,引入变邻域搜索策略,通过交替搜索不同邻域结构来提高算法搜索深度。本文设计采用变邻域搜索策略的HGALNS算法对MDMFVRP-MTW进行求解,该算法采用聚类法生成初始种群来提高初始解的质量,并采用多个不同的“破坏—修复”算子交替搜索来提高算法的局部搜索能力,算法流程如图3所示。
3.1 初始解的构造
3.1.1 初始种群的生成
为了提高初始解的质量,本文采用聚类法生成初始种群,具体步骤如下:
步骤1随机选择若干客户作为聚类簇中心,聚类簇数量与车辆总数成比例,比例系数=需求总量/运力总量。
步骤2计算其余客户到各聚类簇的平均距离,确定距各客户最近的聚类簇及其平均距离d1和次近的聚类簇及其平均距离d2。
步骤3在满足(d2-d1)>0.3d1的客户中,选择距离差最大的客户加入与其距离最近的聚类簇,转步骤5;如果不存在满足条件的客户,则执行步骤4。
步骤4计算客户与各聚类簇的平均距离方差,选择方差最小的客户点加入对应的聚类簇中。
步骤5重复上述步骤,直到所有客户分配完毕。
步骤6按照客户时间窗的最早时间与最晚时间的平均值由小到大对各聚类簇中的客户进行排序,得到初始种群。
3.1.2 初始解的生成
针对3.1.1节构造的初始种群,本文按照“先电动车,后燃油车;先大车型,后小车型”的原则解码构造初始解,在该过程中,燃油车看作为电量无穷大的“电动车”。对初始种群中每条染色体的操作步骤如下:
步骤1在拥有所选车型的配送中心,选择满足首个客户时间窗约束和返回电量约束(服务完客户后,在不违反电池最低荷电状态约束的情况下,至少可返回一个配送中心)的出发配送中心,如果配送中心均不满足条件,则选择下一车型并重复上述操作。
步骤2判断下一客户点是否满足客户服务时间窗、车辆载重和返回电量约束,满足则将该客户添加入路径,重复步骤2,不满足则返回电量约束执行步骤3,否则转步骤4。
步骤3在服务当前客户点后寻找配送中心换电,如果换电后电量可前往下一客户点,则重复步骤2,否则执行步骤4。
步骤4结束当前路径客户分配,按照“运力平衡”原则选择可到达的配送中心返回,如果车辆不可到达,则在其他配送中心换电后前往该配送中心。
步骤5派遣新车辆,重复步骤1~步骤4,直至所有客户划分完毕。
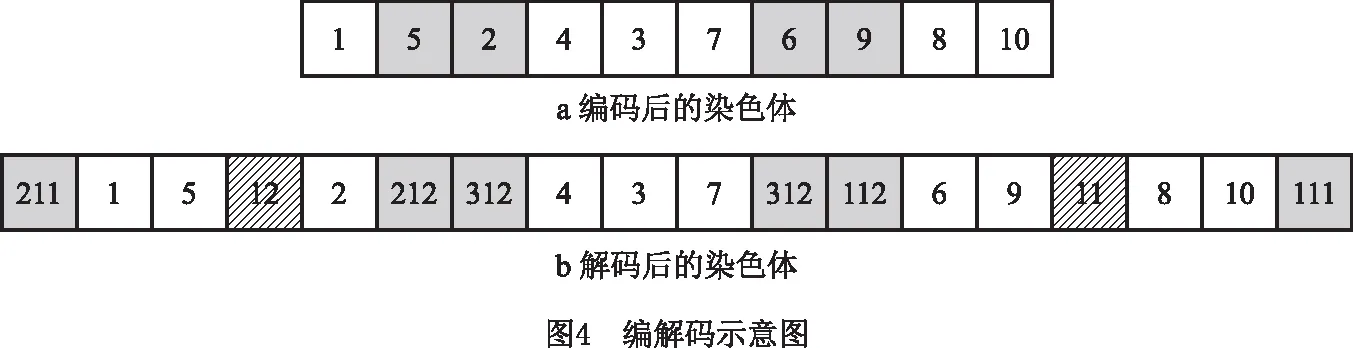
如图4所示,图中1~10表示客户点,11~12表示配送中心。以车辆1路径(211-1-5-12-2-212)为例,车型2车辆从配送中心11出发,依次服务客户1,5后,由于电量不足,前往配送中心12更换电池,然后服务客户2,完成配送服务后返回配送中心12。
3.2 适应度计算与选择
种群中各染色体的适应度可由模型目标函数式(8)构建,适应度
(27)
式中Z为染色体的目标函数值。
选择操作采用精英选择和轮盘赌相结合的策略,选择部分精英个体直接保留进入下一代,剩余数量的个体则由轮盘赌产生,适应度越高,个体越容易被选择。
3.3 交叉操作
本文采用改进子路径交叉操作,交叉过程如图5所示。针对父代染色体S1,S2,在考虑运力平衡约束和配送中心各车型车辆数量约束的基础上,随机选择子路径进行交换,交换后删除所有重复客户,并对路径中因交换缺失的客户进行重插入,具体步骤如下:
步骤1选择待插入客户。
步骤2判断车辆剩余可载重量是否满足客户需求,对于无法满足载重约束的子路径,令插入成本Cm为无穷大。
步骤3计算可插入路径中的所有位置插入成本Cm,客户m在i点和j点之间的插入成本
Cm=Z1·(lim+lmj-lij)+Z2·CTW。
(28)
式中:Z1,Z2为距离权重系数和时间窗惩罚成本权重系数;CTW为m点的时间窗惩罚成本。
步骤4若所有位置插入成本均为无穷大,则执行步骤5,否则选择插入成本最小的位置试插入当前待分配客户,判断后续客户是否满足时间窗约束,并重新分配该子路径上的换电配送中心和返回配送中心位置。如果后续客户未违反时间窗约束,并能返回符合运力平衡的配送中心,则插入当前位置,重复步骤1;否则,令插入成本为无穷大,重复步骤4。
步骤5为当前待插入客户新增一条子路径,选择车型、出发配送中心和满足运力平衡的返回配送中心,步骤如3.1.2节的步骤1和步骤4。
步骤6重复上述操作,直到将所有被移除客户重新插入至路径中。
3.4 破坏—修复操作
本文设计的HGALNS算法的邻域搜索思想是对可行路径进行重复破坏和修复,从而构造新的可行路径,该算法包括3个邻域搜索算子,每个算子包括路径破坏和路径修复两部分。
(1)路径破坏
1)移除随机客户 随机移除10%客户,如图6a所示。
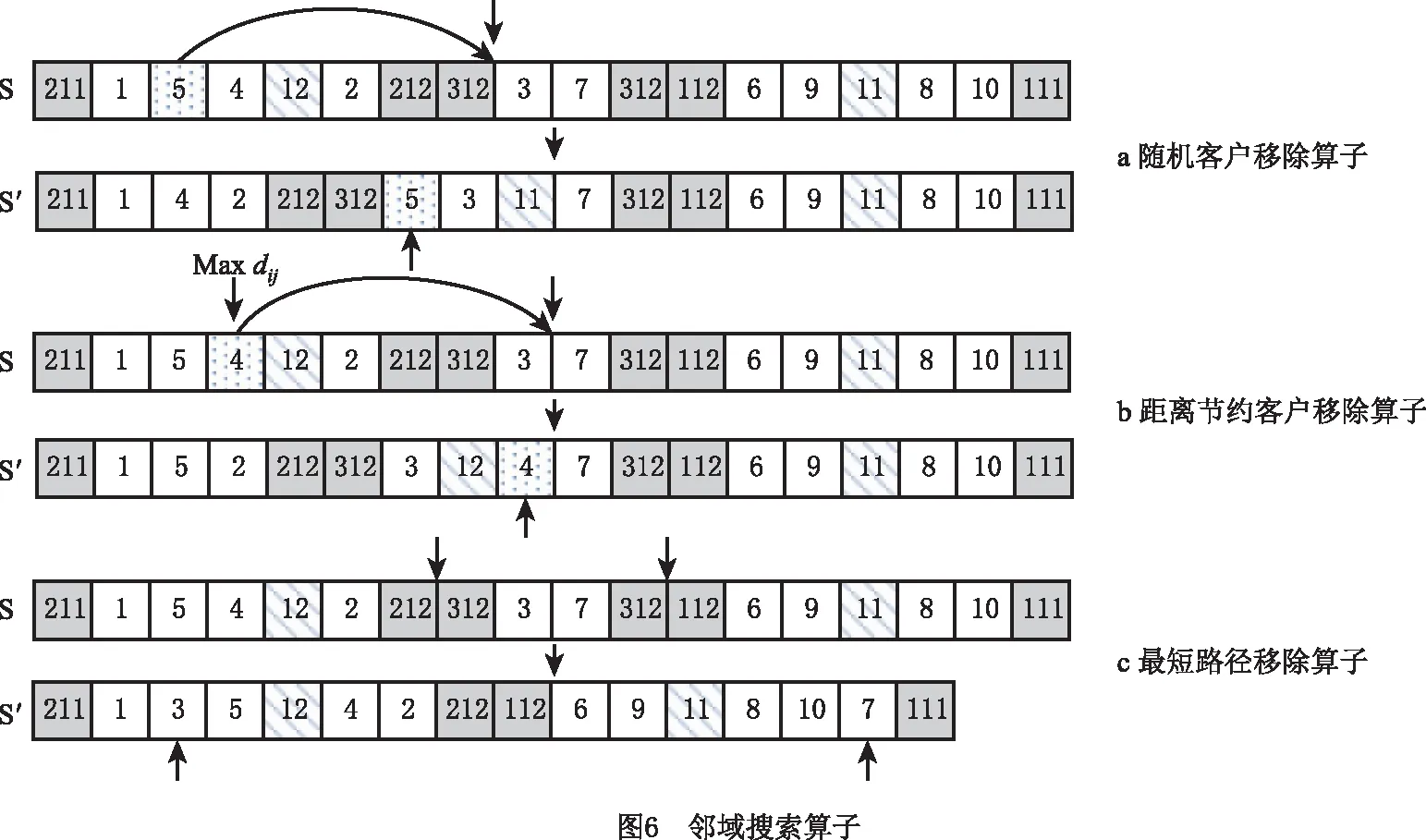
2)移除距离节约客户 移除与前后客户或配送中心的距离之和最大的10%客户,如图6b所示。
3)移除最短路径 移除各个体中客户数量最少的子路径,如图6c所示。
移除客户的目的是破坏路径,移除最短路径的主要目的是减少所使用车辆,降低派遣成本。
(2)路径修复
路径修复的目的是将被移除的客户重新插入路径,具体步骤如3.3节的客户重插入操作
3.5 变邻域搜索策略
为了提高HGALNS算法的深度搜索能力,本文引入变邻域搜索算法中的扰动策略,该策略根据各“破坏—修复”算子运行后最优解的变化情况调整算子的交替搜索顺序和策略。在该策略下,“随机客户破坏—修复”算子作为第一顺序邻域搜索算子的运行次数较高,能够有效提高算法的全局搜索能力。变邻域搜索策略伪代码如下:
Variable neighborhood search strategy
Input:Ik={I1,I2,…,Im}: destroy and repair operators, Imis the mth destroy and repair operator。
1 s←Current Solution;
2 s′←s;
3 m=1;
4 while m 5 Destroy and repair operators:st←Im(s′); 6 if f(st) 7 s′←st; 8 m=1; 9 else 10 m++; 11 end 12 end 13 returns′ 为了验证本文模型的有效性及本文所设计算法的性能,首先将HGALNS求解结果与Gurobi精确算法求解结果进行对比;然后采用HGALNS算法分别求解本文问题涉及的带软时间窗的多中心车辆路径问题(Multiple Depot Vehicle Routing Problem with Soft Time Windows, MDVRPSTW)、带硬时间窗的车辆路径问题(Multiple Depot Vehicle Routing Problem with Hard Time Windows,MDVRPHTW)、带时间窗的电动车车辆路径问题(Electric Vehicle Routing Problem with Time Windows, EVRPTW),并与其他启发式算法的求解结果进行对比验证;最后设计本文问题算例,并对影响方案制定的主要因素进行敏感性分析。本文算法编程采用MATLAB R2018b,操作系统为Windows10,电脑内存为8 G,CPU为Intel i7-7700 M,主频为3.6 GHz。经过反复测试,本文算法涉及的参数设置为:交叉概率Pc=0.95,代沟GGAP=0.95。 Gurobi采用Python3.9进行编程,运行环境与HGALNS相同,使用的算例为Solomon系列VRPTW标准算例。因为Gurobi在超过15个节点数量的算例中求解时间较长,所以设置Gurobi的最大运行时间为18 000 s,当达到最大运行时间时,输出Gurobi当前求得的最好解。求解结果如表1所示,其中n,d分别为客户和配送中心的数量,Obj为Gurobi和HGALNS的求解结果,Gap为HGALNS和Gurobi求解结果偏差的平均值。 表1 HGALNS与Gurobi求解结果的对比 由表1可知,HGALNS较Gurobi在求解效率上有明显优势,其可在30 s内求得接近或优于Gurobi的解决方案,而Gurobi在客户规模超过15的算例中的求解速度很慢,且在规定时间内的求解质量较差。HGALNS与Gurobi的求解平均偏差为0.41%,证明了本文模型的有效性以及HGALNS算法较高的求解效率。 本节对HGALNS与其他启发式算法的性能差距进行验证。因为目前没有MDMFVRP-MTW算例,所以对已有文献中与MDMFVRP-MTW相关的基本问题进行3组数值实验。 4.2.1 实验1 为了验证HGALNS与LNS算法的性能差距以及HGALNS求解MDVRPSTW的有效性,采用本文算法对文献[23]中的MDVRPSTW算例进行求解,并与LNS算法、考虑时空距离的混合遗传变邻域算法(Hybrid Genetic Algorithm with Variable Neighborhood Search considering the Temporal-Spatial distance,HGAVNS_TS)[23]进行对比,该算法运行环境与本文相同。表2所示为LNS,HGAVNS_TS,HGALNS的求解结果,其中Pre-Best为前两种算法的最好解,Gap为本文算法求解的最优值相对Pre-Best的改进幅度,Avg.Gap为各算法的最优值(best)、平均值(Avg)和Pre-Best偏差的平均值。 表2 HGALNS与文献[23]求解结果对比 由表2可知,在与LNS的求解结果对比中,本文HGALNS求解最优值、平均值较LNS的改善幅度分别达到7.78%,7.04%,求解时间也明显优于LNS,证明了本文设计的HGALNS及变邻域搜索策略的有效性。 对比已有文献算法的求解结果,在求解质量上,HGAVNS_TS,HGALNS的求解最优值与Pre-Best的平均偏差分别为0.58%,-3.7%,最优值的改善幅度为4.28%,求解平均值与Pre-Best的平均偏差分别为2.53%,-0.28%,求解平均值的改善幅度为2.81%,而且HGALNS算法求得全部12个算例中10个算例的最好解。在求解时间上,相同运行环境下,本文算法的求解时间短,在中小规模算例中的求解时间略优于HGAVNS_TS,而且随着算例客户规模的增加,算法求解时间明显优于其他两种启发式算法。通过对比分析说明,HGALNS算法的性能优于LNS和HGANLS_TS。 4.2.2 实验2 选择文献[24-25]的算法进行对比分析。表3所示为MPMSFLA[24],DFCAN[25]与本文HGALNS对CORDEAU等[26]提出的MDVRPTW标准算例的求解结果,其中DFCAN[25]未提供运行时间数据,因此未列出。 由表3可知,在求解质量方面,本文HGALNS的求解结果与Pre-Best的平均偏差为1.92%;在求解时间方面,HGALNS求解大规模算例的最长运行时间为23.18 min,对于物流企业制定一个整体配送方案来说,这个时间范围完全可以接受。通过以上对比分析,验证了HGALNS求解MDVRPHTW问题的有效性。 4.2.3 实验3 选择文献[27]验证HGALNS求解EVRPTW问题的有效性,以及与文献中使用的节约—禁忌搜索混合算法(节约—禁忌搜索(Clarke-Wright saving and Tabu Search, CW-TS)混合算法)的性能差距,该算例包括1个配送中心、2个换电站和25个客户。表4所示为CW-TS算法[27]和HGALNS运行10次的结果,其中L为车辆行驶总距离,P为时间窗惩罚成本,C为总成本,Avg为各算例数值的平均值,Range为10次运行结果的方差,Gap为改进比例。 表4 HGALNS与文献[27]求解结果对比 由表4可知,在求解质量方面,CW-TS与HGALNS算法10次求解的平均值分别为8 080.70,8 012.49,本文算法求得的时间窗惩罚成本较CW-TS改进了33.94%,总成本较CW-TS改进了0.84%;在求解稳定性方面,CW-TS和HGALNS 10次求解结果的方差分别为76 909.41,9 821.85,HGALNS求解稳定性较好。综上所述,本文算法在求解质量和稳定性上均优于CW-TS,进一步验证了本文HGALNS的有效性。 通过3组数值实验说明,本文算法能够在相对较短的时间内求得问题的较优解,求解结果具有较好的稳定性,HGALNS的求解效率接近或优于以上算法。 4.3.1 算例设计 由于目前没有MDMFVRP-MTW算例,本文在MDVRPTW标准算例的基础上进行改编,改编规则为:①时间窗参数/60(单位:h);②服务时间参数/60(单位:h);③客户需求量(3/k),其中k为算例中各车型中的最大车辆载重量参数(单位:t);④坐标参数/2(单位:km)。 客户中前62.5%为软时间窗客户,后37.5%为硬时间窗客户。车辆参数如表5所示,每个配送中心3种车型的车辆数分别为算例中车辆数量的1/2,1/4,1/3(向上取整),两种电动车的可替换电池数分别为2和3。计算燃油车油耗成本使用的CMEM模型相关参数参考文献[28],算例中涉及的其他参数如表6所示。 表5 车辆参数 续表5 表6 算例其他相关参数 4.3.2 算例求解 (1)算例参数设置分析 为确定Z1和Z2的参数设置,本文对Z1和Z2的不同参数组合进行对比实验分析。表7所示为使用本文HGALNS对5组Z1,Z2参数进行不同规模算例的求解结果,其中Best为5种参数组合的最好解。可见,5组参数的Gap平均值分别为55.86%,8.61%,2.83%,0.87%,17.16%,而且[0.75,0.25]取得了其中7个算例的最好解,因此选择表现更好的[0.75,0.25]作为后续实验的参数值。 表7 参数设置求解结果对比 (2)不同规模的算例求解 表8所示为HGALNS对不同规模算例的求解结果,其中N表示电动车换电次数,Ratio表示优化结果中使用的3种车型车辆数量,Ctotal表示总成本,Avg表示各项成本与总成本比值的平均值。可见,当算例为n≤72的中小规模算例时,优化方案中使用的车辆均为电动车,随着客户规模的增加,燃油车的使用数量显著增加,证明了电动车在中小规模配送中的经济性;在成本结构方面,车辆派遣成本、油耗成本、电动车能耗成本、时间窗惩罚成本与总成本比值的平均值分别为75.08%,7.85%,6.96%,10.45%。 表8 HGALNS求解不同算例的结果 4.3.3 敏感性分析 (1)不同返回策略的影响 为验证本文所提运力平衡的车辆返回策略的合理性,对不同返回规则下的多组算例进行求解分析。表9所示为3种返回策略在不同算例下的求解结果,其中Best为3种策略下总成本的最优值,Gap为C与Best的偏差,Max_L和Min_L表示配送结束时各配送中心拥有的运力与其起始运力比值的最大值和最小值。可见,在10组不同规模算例中,3种返回策略与Best值偏差的平均值分别为2.46%,3.52%,0.00%,其中运力平衡的返回策略在每组算例中均能求得最好解;在运力的稳定性方面,运力平衡返回策略的最小和最大运力比的平均值分别为78.77%,119.24%,各配送中心运力具有较好的稳定性。虽然返回原中心和各车型车辆数平衡返回策略均能保持运力绝对平衡,但是可选择的返回方案较少,经济性较差,而本文所提运力平衡的返回策略能够保证运力相对平衡,可有效降低总成本。 表9 不同返回策略的敏感性分析 (2)运力平衡系数的影响 为分析不同运力平衡系数对制定配送方案的影响,设置4组不同的运力平衡系数分别进行求解,求解结果如表10所示,其中Best为4组运力平衡系数下平均总成本的最优值,Gap为C与Best的偏差。可见,4组不同的运力平衡系数在不同算例下求得的配送成本与最优值的平均偏差分别为5.23%,0.83%,0.15%,0%,即随着运力平衡系数的松弛,满足运力平衡的车辆返回方案增加,总配送成本会有所降低。当运力平衡系数为[0,-]时,运力平衡约束完全松弛,取到每组算例的最优值。因此,运力平衡系数的变化会影响配送方案的制定。 表10 运力平衡敏感性分析 (3)混合时间窗比例的影响 为分析不同混合时间窗客户比例对配送方案的影响,对不同混合时间窗客户比例的多组算例进行求解分析。表11所示为10组算例的求解结果,其中S∶H为软时间窗客户数和硬时间窗客户数之比。可见,4组不同混合时间窗客户比例下求得的配送成本的平均值与最优值的偏差分别为18.62%,9.08%,3.44%,0.00%,即随着软时间窗客户数量比例的增加,求得的总配送成本的平均值有所降低,而且当软时间窗客户比例为100%时求得最优值。当S∶H=0%∶100%时本文问题为VRPHTW,此时客户时间窗类型均为硬时间窗;当S∶H=100%∶0%时本文问题为VRPSTW,此时客户时间窗类型均为软时间窗,VRPHTW下求解得到的总配送成本平均值较VRPSTW增加了18.62%。因此,混合时间窗客户比例变化对配送方案的制定具有重要影响。 本文针对MDMFVRP-MTW进行研究,得到以下结论: (1)所建立的MDMFVRP-MTW优化模型,不仅考虑了多中心联合配送、混合车队、客户混合时间窗等特征,还考虑了配送中心运力平衡返回规则,虽然增加了模型复杂度和问题求解难度,但是更符合现实配送生产活动。 (2)所设计的HGALNS采用聚类法生成初始解,基于运力平衡的返回策略设计交叉、变异算子,并引入变邻域搜索结构和LNS算法的移除和插入算子进行搜索优化,有效提升了算法的局部搜索能力。 (3)通过分析不同返回策略的敏感性表明,返回原配送中心和各车型车辆数平衡返回策略由于可选择返回方案有限,运营成本较高,而运力平衡的返回策略允许配送中心适当调整运力,能够有效降低运营成本;通过分析不同运力平衡系数的敏感性表明,随着运力平衡系数的松弛,满足运力平衡的车辆返回方案增加,总配送成本有所降低;通过分析不同混合时间窗客户比例的敏感性表明,随着软时间窗客户在客户总体中所占比例的增加,总配送成本有所降低。 基于本文研究得出以下管理启示: (1)对于仅使用燃油车作为载运工具的物流企业,适当引入电动车能够有效降低企业运营总成本;对于使用电动车和燃油车混合车队的物流企业,应考虑合理配置电动车与燃油车的车型和数量,以使企业总成本最低。 (2)由于电动车存在里程约束,企业应结合订单数量、位置分布和客户时间窗等信息,合理制定当期混合车队结构,盲目使用电动车取代燃油车配送可能会造成效益背反。 (3)对运力平衡策略的分析表明,拥有多个配送中心的企业在多中心联合配送的基础上,采用运力平衡返回策略适当调整运力分布能够有效降低企业配送成本。 未来将针对配送车辆速度连续变化情况下的多中心混合车队车辆路径优化问题进行研究。4 数值分析
4.1 与Gurobi求解结果的对比分析
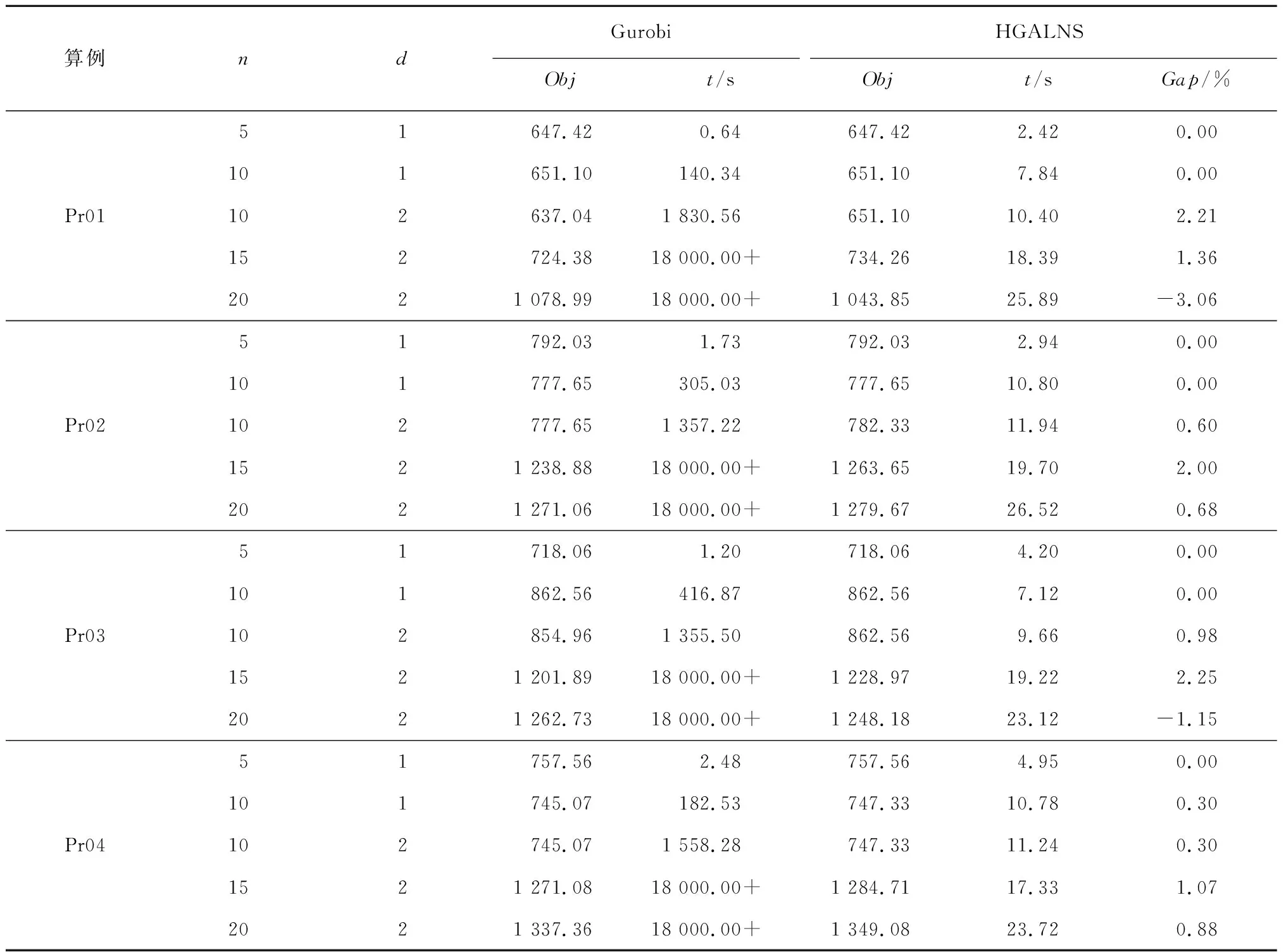
4.2 算法验证

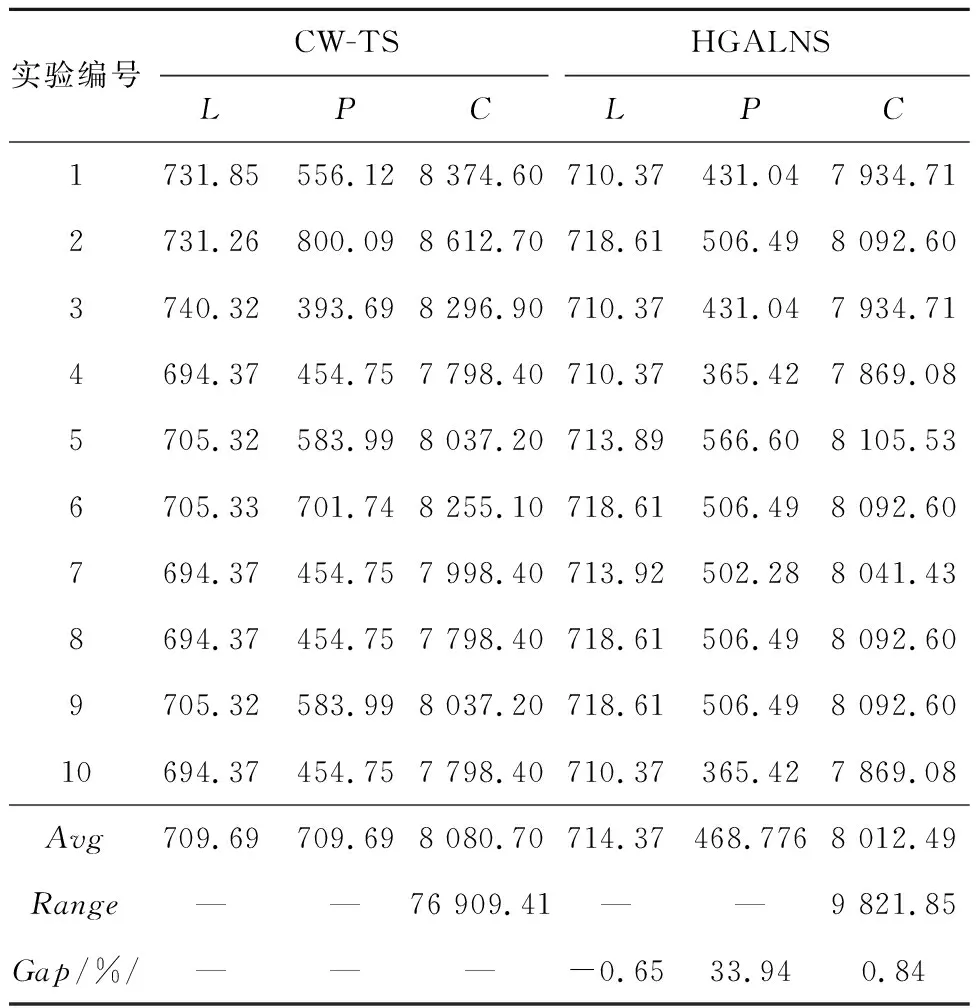
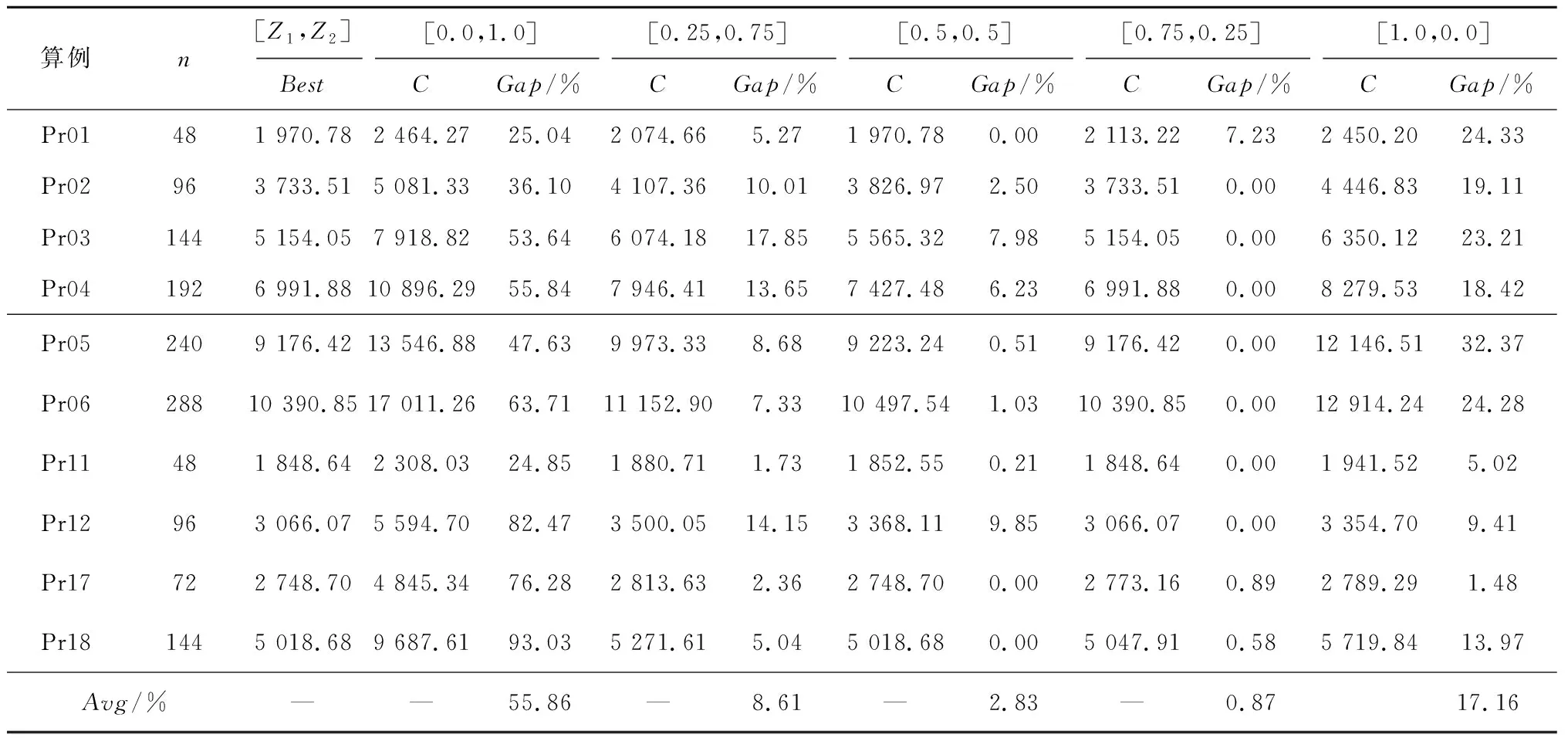
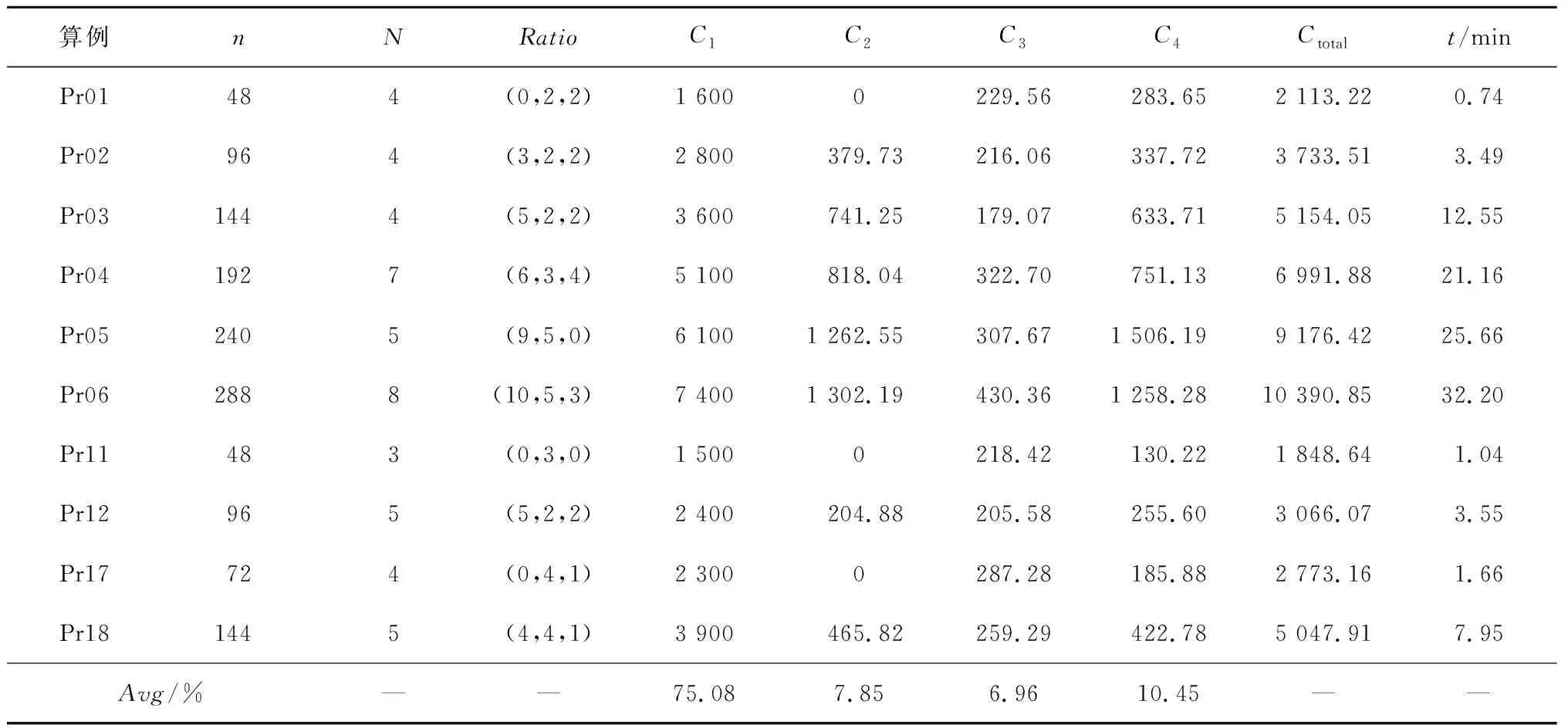
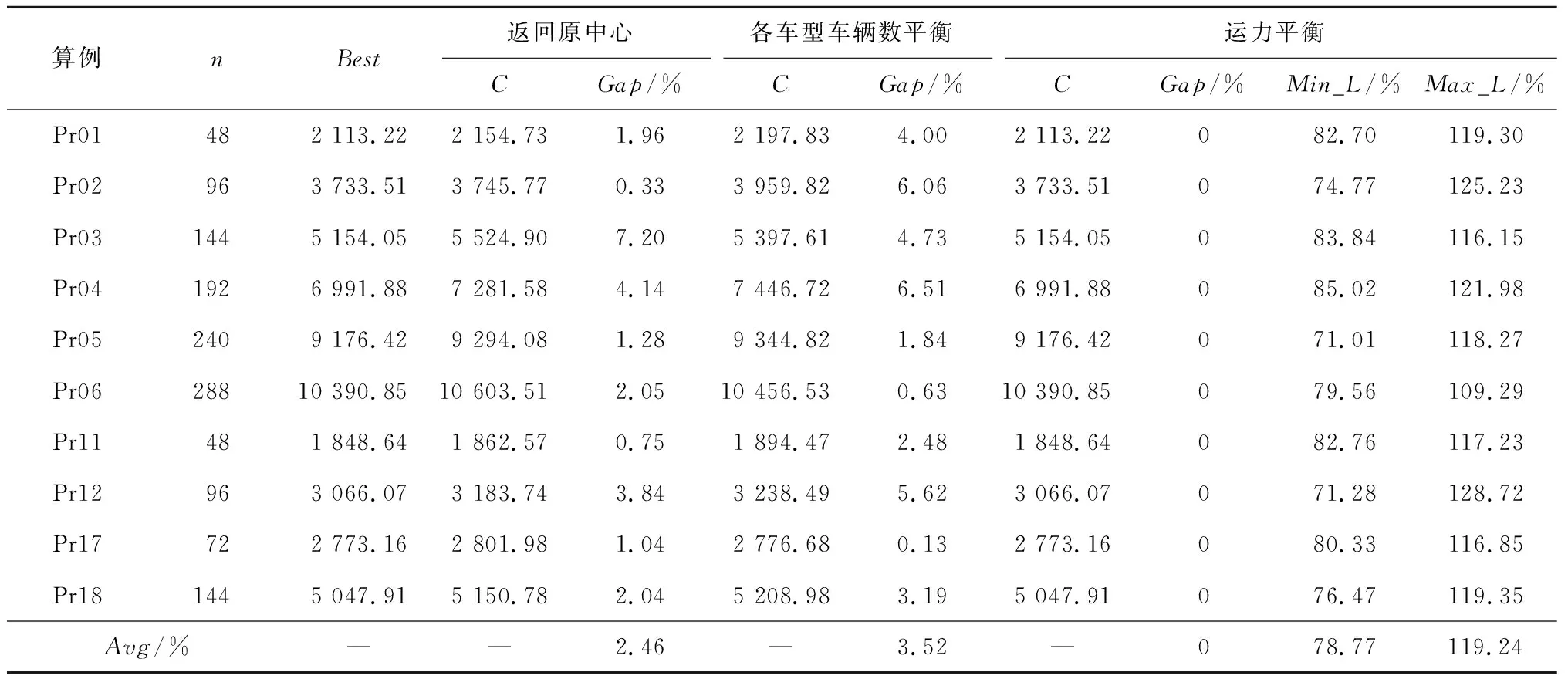
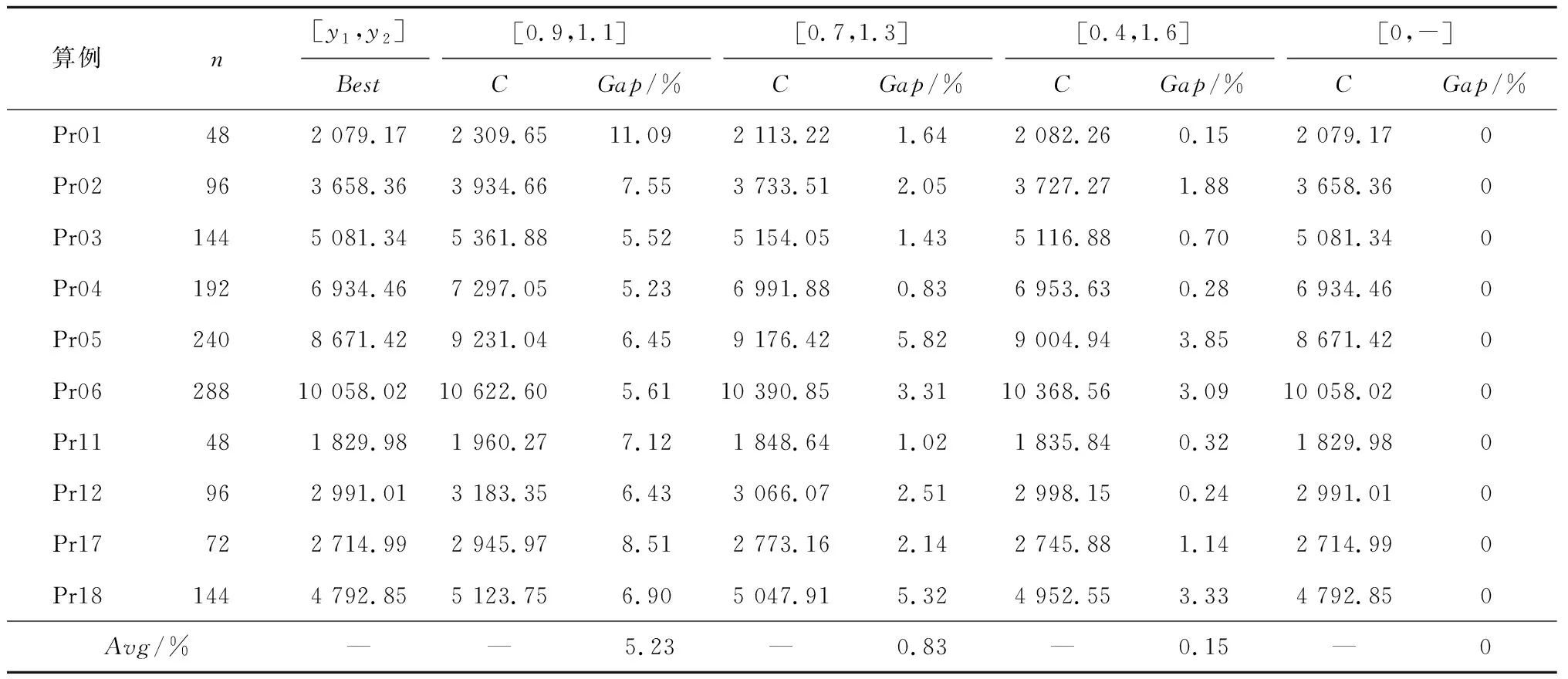
4.3 算例分析
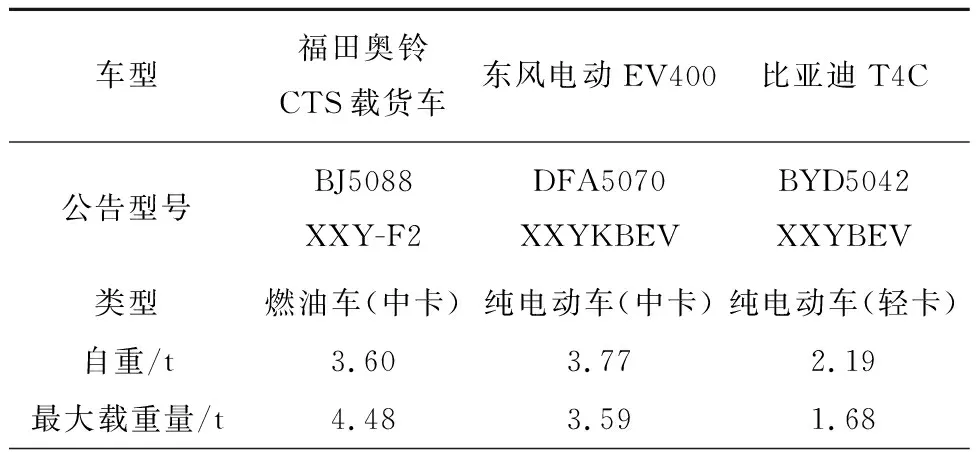
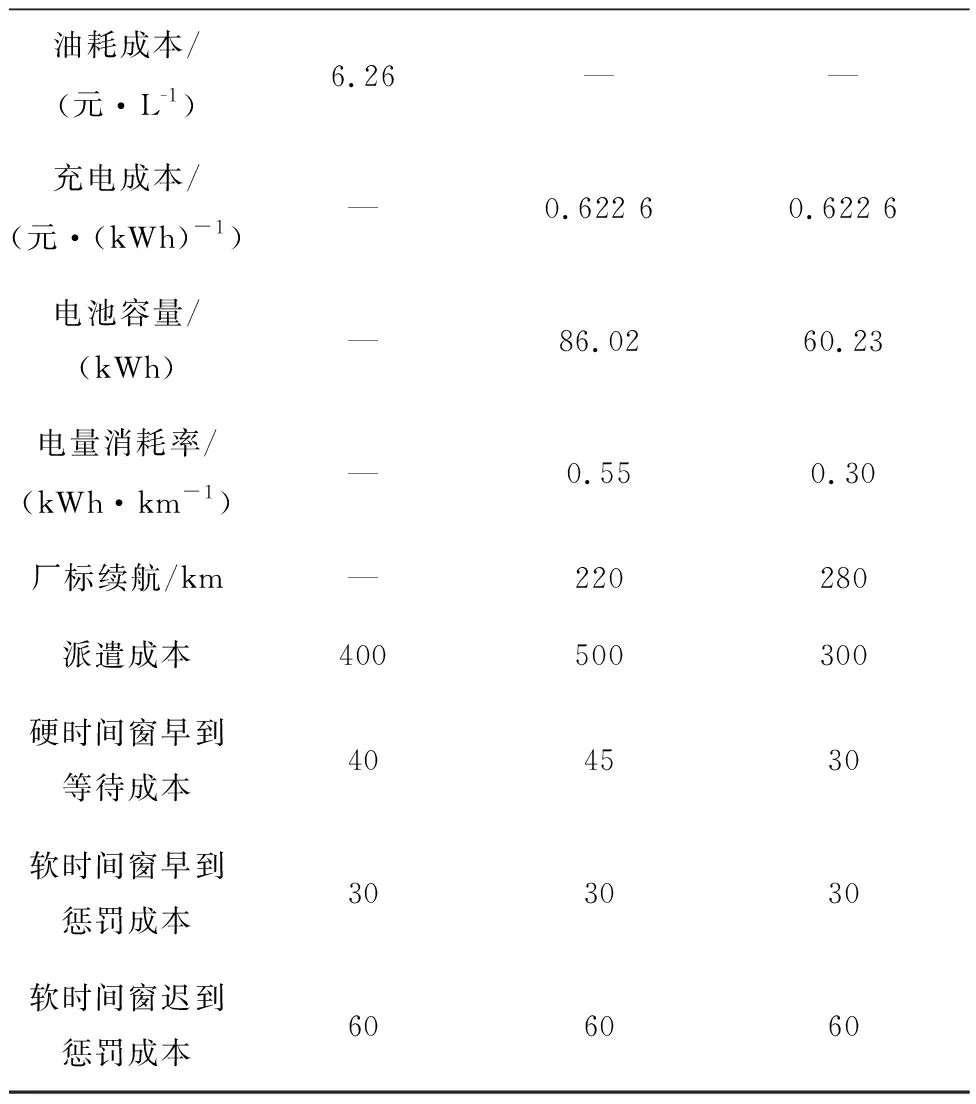

5 结束语
