基于虚拟中心距原理的鼓形蜗杆砂轮成形修整方法

李国龙,冉全福,何 坤,王时龙,操 兵

(1.重庆大学 机械传动国家重点实验室,重庆 400044;2.重庆工商大学 制造装备机构设计与控制重庆市重点实验室,重庆 400067)

0 引言

面齿轮副主要应用于航空领域(如直升机减速器),具有传动比大、重合度高、结构紧凑、动力分流效果好、对安装误差不敏感等优点[1]。作为直升机动力传动装置的核心零件之一,面齿轮必须在高速、重载的工况下保持优良的性能,这极大提高了对面齿轮齿面精度的要求。

磨削是提高齿轮齿面精度的核心工序。面齿轮磨削加工主要有碟形砂轮磨削和蜗杆砂轮磨削两种方法,相比碟形砂轮磨削,蜗杆砂轮磨削可实现连续分度,具有更高的加工效率。LITVIN等[2-5]研究了面齿轮蜗杆砂轮磨削工艺,设计了面齿轮蜗杆砂轮磨齿机,提出计算蜗杆砂轮型面和避免蜗杆型面奇异点的方法,阐述了面齿轮蜗杆砂轮的成形修整和平面修整原理。李政民卿等[6]和王延忠等[7]研究面齿轮滚磨刀具的基蜗杆型面计算方法,但未对其型面的奇异性进行详细分析。高金忠等[8-9]在前人基础上研究了齿数、模数等设计参数影响面齿轮滚磨刀具基蜗杆齿廓奇异点位置的规律,分别基于单参数包络和双参数包络提出两种蜗杆砂轮修整方法,然而该方法尚停留在理论阶段。唐进元等[10-12]基于微分几何和啮合原理研究了面齿轮齿面和蜗杆砂轮型面的曲面特性,给出磨削过程中二者曲面点的对应关系;此外,针对现有面齿轮蜗杆砂轮磨削方法中可能出现面齿轮工作齿面不被完全覆盖的现象,提出面齿轮蜗杆砂轮磨削多步法,并进行了VERICUT仿真验证,仿真结果证明多步磨削可以实现面齿轮齿面全覆盖。郭辉等[13-14]研究了在六轴数控蜗杆砂轮磨齿机磨削面齿轮的方法,选择成形金刚滚轮修整蜗杆砂轮,该方法在原理上存在误差,只能得到近似的砂轮型面;另外,提出利用标准锥面滚轮修整面齿轮蜗杆砂轮的方法,该方法虽然提高了金刚滚轮的通用性,但是每次只能修整蜗杆砂轮齿面上的一条螺旋线,修整效率较低。

综上所述,面齿轮蜗杆砂轮磨削的主要难点是蜗杆砂轮型面的计算和修整。在蜗杆砂轮型面计算方面,目前的研究大都基于啮合原理,需要求解复杂的啮合方程且计算结果受到奇异点的限制;在蜗杆砂轮修整方面,现有面齿轮蜗杆砂轮修整方法大多需要在专用机床上进行,缺乏通用性。

为此,本文研究了在普通蜗杆砂轮磨齿机上磨削面齿轮时的蜗杆砂轮型面计算和修整问题。首先,讨论了磨削面齿轮的鼓形蜗杆砂轮演变计算方法,采用母线螺旋扫掠方式建立鼓形蜗杆砂轮型面方程;其次,提出基于虚拟中心距加工原理的鼓形蜗杆砂轮成形修整方法,通过四轴联动方式实现砂轮偏摆,从而完成鼓形蜗杆砂轮的修整;最后,利用VERICUT对所提修整方法进行了仿真验证。

1 面齿轮磨削用鼓形蜗杆砂轮型面计算

1.1 面齿轮蜗杆砂轮型面计算原理

面齿轮蜗杆砂轮的型面计算方法基于共轭曲面包络理论,通过求解啮合方程对蜗杆砂轮型面进行解析计算。从共轭包络的角度看,面齿轮蜗杆砂轮型面由插齿刀经单参数包络而成,插齿刀的端面齿廓为标准渐开线,如图1所示,齿廓rs1的方程表示为

(1)

式中:rb为插齿刀基圆半径;θs和us为插齿刀齿面的Gauss坐标;“+”对应右侧齿形,“-”对应左侧齿形;θos为插齿刀齿槽半角,

(2)

式中Ns和α0分别为插齿刀齿数和分度圆压力角。

插齿刀包络形成蜗杆砂轮齿面时,插齿刀与蜗杆砂轮之间处于假想的内啮合状态,如图2所示。Om-XmYmZm为与插齿刀支架固联的固定坐标系,Os1-Xs1Ys1Zs1为插齿刀的运动坐标系;Oa-XaYaZa为与蜗杆砂轮支架固联的固定坐标系,Ow1-Xw1Yw1Zw1为蜗杆砂轮的运动坐标系;On1-Xn1Yn1Zn1为辅助坐标系;Ews为蜗杆砂轮轴线与插齿刀轴线之间的最短距离,λw为蜗杆砂轮螺旋升角,φs和φw分别为插齿刀和蜗杆砂轮的转角,二者之间的关系为

(3)

式中Ns和Nw分别为插齿刀齿数和蜗杆砂轮头数。

蜗杆砂轮型面rw1在坐标系Ow1-Xw1Yw1Zw1中表示为:

(4)

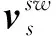
rw1(θs,φs)=rw1(φs,θs,us(φs,θs))。

1.2 面齿轮磨削用鼓形蜗杆砂轮演变计算法

1.2.1 鼓形蜗杆砂轮型面演变过程

利用共轭曲面包络原理计算面齿轮蜗杆砂轮型面时,需要求解复杂的啮合方程,且计算结果受奇异点的限制。本文类比齿条插刀向普通圆柱蜗杆砂轮演变的过程,将面齿轮插齿刀演变为鼓形蜗杆砂轮,用于面齿轮的连续展成磨削。

建立由插齿刀向鼓形蜗杆砂轮演变成形的坐标系,如图3所示。其中,Ow2-Xw2Yw2Zw2为与鼓形蜗杆砂轮固连的动坐标系,Ob-XbYbZb和On2-Xn2Yn2Zn2均为固定坐标系且YbObZb平面和Yn2On2Zn2平面分别与蜗杆轴截面和法截面重合,Os2-Xs2Ys2Zs2为假想齿形线的运动坐标系,Op-XpYpZp为假想齿形线的固定坐标系。

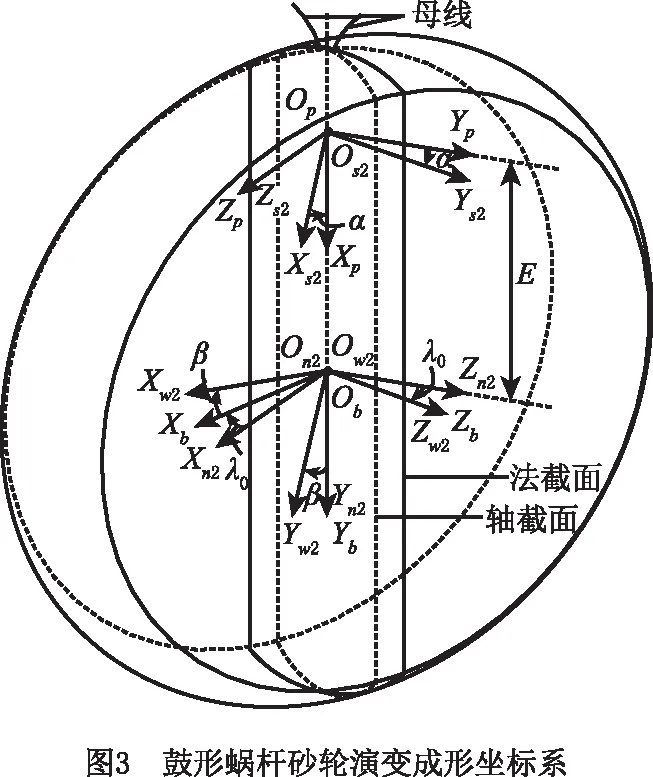
在鼓形蜗杆基体法截面上构造一对与插齿刀端面截廓一致的齿形线rs2,该齿形线方程在坐标Os2-Xs2Ys2Zs2中表示为

rs2(θ)=

式中:rb为插齿刀基圆半径;θ0为插齿刀齿槽半角;θ为渐开线变参数;“+”对应右侧齿形,“-”对应左侧齿形。

以该对齿形线为母线,使母线一方面在法截面内绕Os2Zs2轴匀速旋转,另一方面整体绕蜗杆轴线Ow2Zw2匀速旋转,转角分别为α和β,则从坐标系Os2-Xs2Ys2Zs2到Ow2-Xw2Yw2Zw2的变换矩阵为

(7)

式中:λ0为蜗杆轴截面和法截面之间的夹角,即名义螺旋升角;E为OpYp轴与On1Zn1轴之间的最短距离,其值由蜗杆砂轮实际尺寸决定,可随蜗杆砂轮最大外径的变化而变化,使蜗杆砂轮径向尺寸不受插齿刀尺寸的限制。

当α与β满足α/β=Nw/Ns(Ns为插齿刀齿数,Nw为蜗杆头数)的关系时,母线便可在鼓形蜗杆基体上扫掠形成鼓形蜗杆砂轮螺旋面rw2,表示为

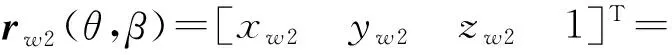
(8)

1.2.2 鼓形蜗杆砂轮的螺旋升角

鼓形蜗杆螺旋升角(λw)定义为蜗杆螺旋线上某点的切向量与该点所在端截面的夹角。令鼓形蜗杆砂轮母线与分度圆交点为Q(-r,0,0),其中r表示齿形线分度圆半径,Q点经过1.2.1节所述的螺旋运动可形成一条螺旋线L(如图4),螺旋线L的方程为

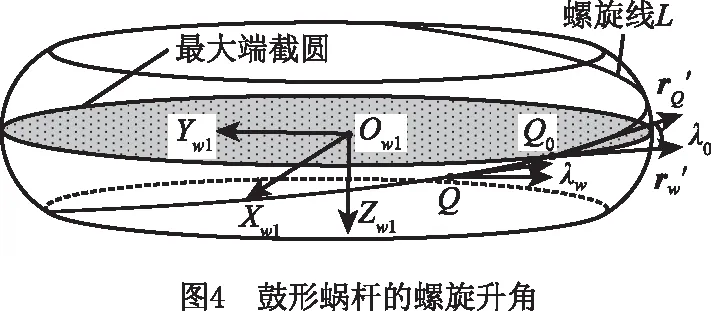
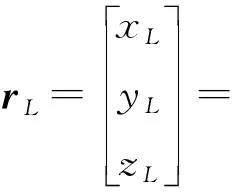
(9)

Q点在螺旋线上的任意位置时,对β求偏导,得螺旋线在其任意点的切矢量为

(10)

鼓形蜗杆上过Q点的端截圆在Q点的切矢量为

(11)

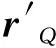
(12)

可见鼓形蜗杆的螺旋升角λw随着螺旋线上点位置的变化而不断变化,取螺旋线与鼓形蜗杆最大端截圆交点Q0处的螺旋升角为鼓形蜗杆砂轮的名义螺旋升角,名义螺旋升角即为鼓形蜗杆轴截面和法截面的夹角,用λ0表示,将β=0代入式(12)并化简得

(13)

1.3 演变法与传统共轭包络法的计算实例

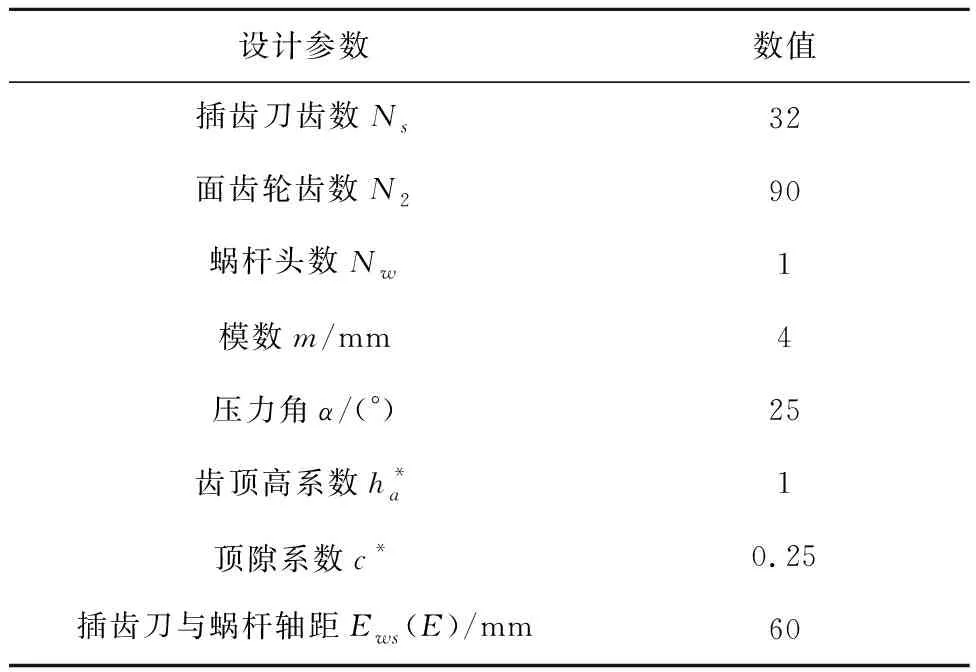
表1 蜗杆砂轮设计参数

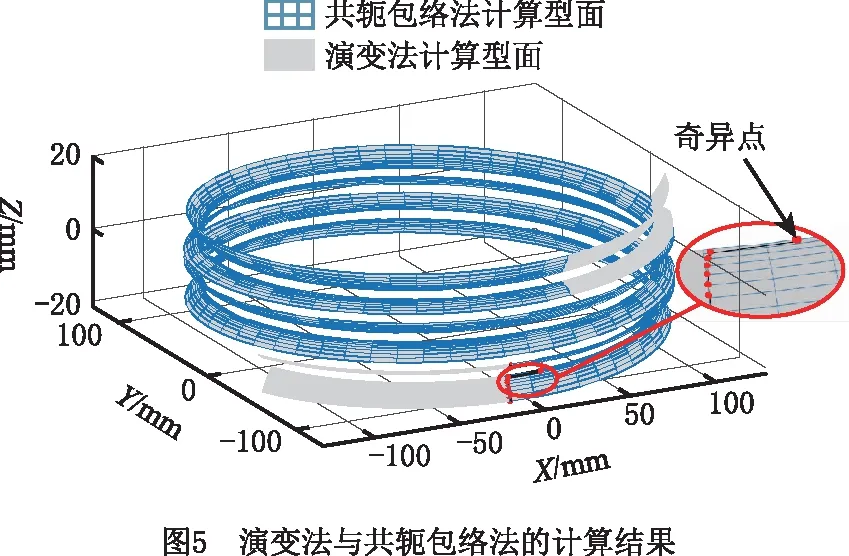
传统共轭包络法所得蜗杆砂轮型面用rw1(θs,φs)表示,演变法所得鼓形蜗杆砂轮型面用rw2(θ,β)表示,在包络法与演变法的两个坐标系统中,如果能使两者蜗杆砂轮的动坐标系Ow1-Xw1Yw1Zw1和Ow2-Xw2Yw2Zw2始终保持重合,并使θs=θ,φs=β,则两种方法所得的蜗杆砂轮型面上的点一一对应,二者的计算偏差可以表示为演变法所得型面点与共轭包络法所得型面点的矢量差在蜗杆砂轮型面法向上的投影,即

e=[rw2(θ,β)-rw1(θs,φs)]·nw1。

(14)

式中nw1为包络法所得蜗杆砂轮型面的法向量,

nw1=Lws(φs)ns。

(15)

式中:Lws(φs)为包络法中的坐标变换矩阵Mw1s1的3阶前主子矩阵;ns为插齿刀齿面的单位法向量。

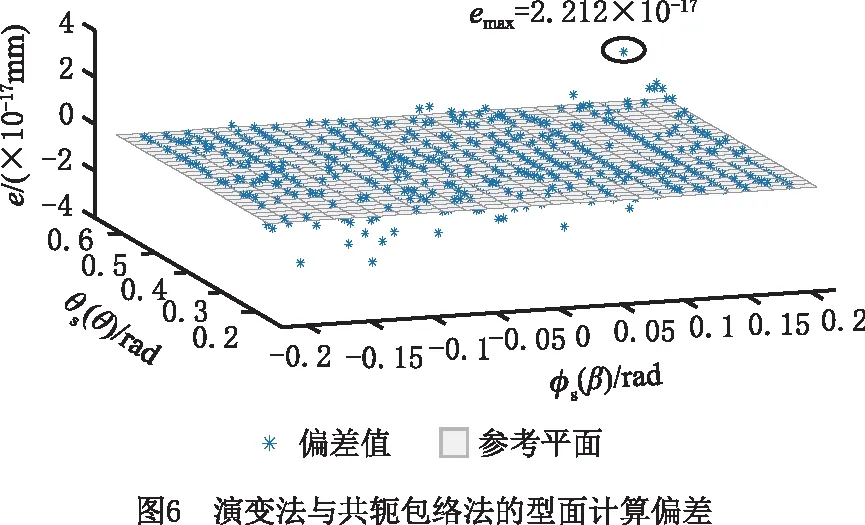
以单侧齿面为例,计算演变法与共轭包络法的型面偏差,如图6所示。可见,型面计算偏差的最大值为2.212×10-17mm,说明演变法计算鼓形蜗杆砂轮时具有较高的计算精度,且相对传统共轭包络法可避免求解复杂的啮合方程,其计算结果不受奇异点限制。

2 鼓形蜗杆砂轮的成形修整方法

2.1 鼓形蜗杆砂轮成形修整运动

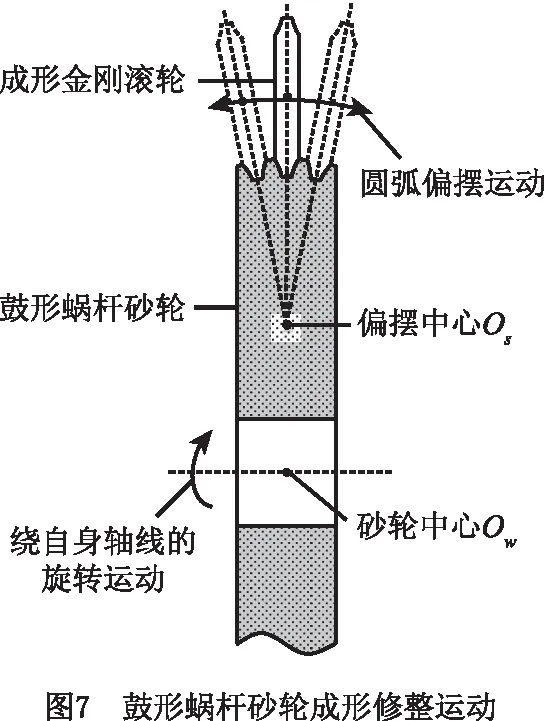
因为鼓形蜗杆砂轮型面由其法截面上的母线经螺旋运动扫掠而成,所以可以利用与母线轮廓相同的成形金刚滚轮,在蜗杆砂轮法截面上对其进行修整。图7所示为成形金刚滚轮在鼓形蜗杆砂轮法截面上修整蜗杆砂轮的运动示意图,鼓形蜗杆砂轮的成形修整运动实质上与式(8)描述的螺旋扫掠运动一致。一方面,鼓形蜗杆砂轮绕其轴线旋转,对应1.2.1节螺旋扫掠运动中母线绕蜗杆轴线的旋转运动;另一方面,鼓形蜗杆砂轮的外缘轮廓为圆弧而非直线,因此以成形金刚滚轮在砂轮轴向相对于砂轮的圆弧偏摆运动为修整冲程运动,偏摆中心Os与砂轮中心Ow不重合,该修整冲程运动对应1.2.1节螺旋扫掠运动中母线在法截面绕OsZs轴的旋转运动。

2.2 基于普通蜗杆砂轮磨齿机的成形修整方法

常用的普通圆柱齿轮蜗杆砂轮磨齿机结构如图8所示,主要的运动轴有X1径向进给轴、Y1切向进给轴、Z1轴向进给轴,以及A1刀架回转轴、B1砂轮旋转轴、C1工件旋转轴,可以实现X1,Y1,Z1,A1,B1,C1六轴联动。除此之外,还有B2滚轮旋转轴和C2滚轮偏摆轴。

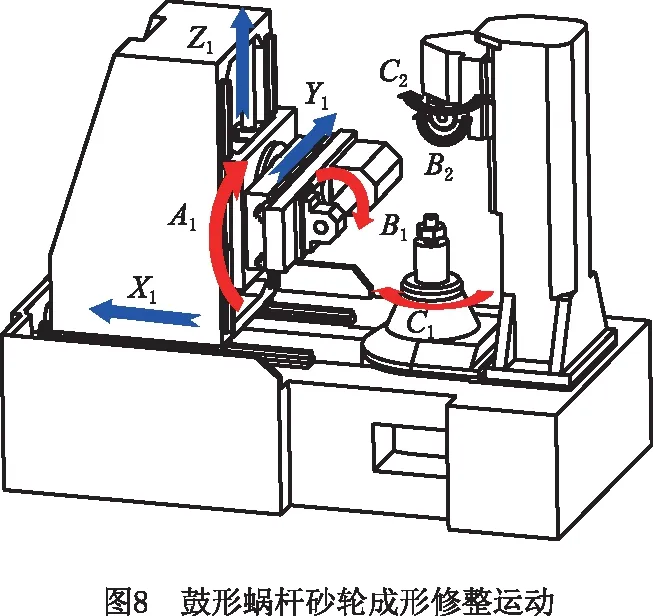
由于普通蜗杆砂轮磨齿机的金刚滚轮偏摆轴C2的偏摆角度有限,无法满足修整运动所需的大幅度偏摆的要求,要在不改变机床整体结构的情况下,在普通蜗杆砂轮磨齿机上对鼓形蜗杆砂轮进行修整,考虑利用砂轮的运动代替滚轮的偏摆实现二者的相对运动以完成修整冲程。如图9所示,在修整时将金刚滚轮置于砂轮正上方,使蜗杆砂轮在竖直平面相对金刚滚轮作偏心摆动,偏摆中心为Os,基于虚拟中心距加工原理[15-16],将砂轮的偏心摆动分解为两个运动,一是砂轮绕A1轴中心OA转动,由刀架回转轴A1实现,二是砂轮在Y-Z平面的平动,由切向进给轴Y1和轴向进给轴Z1联动实现。

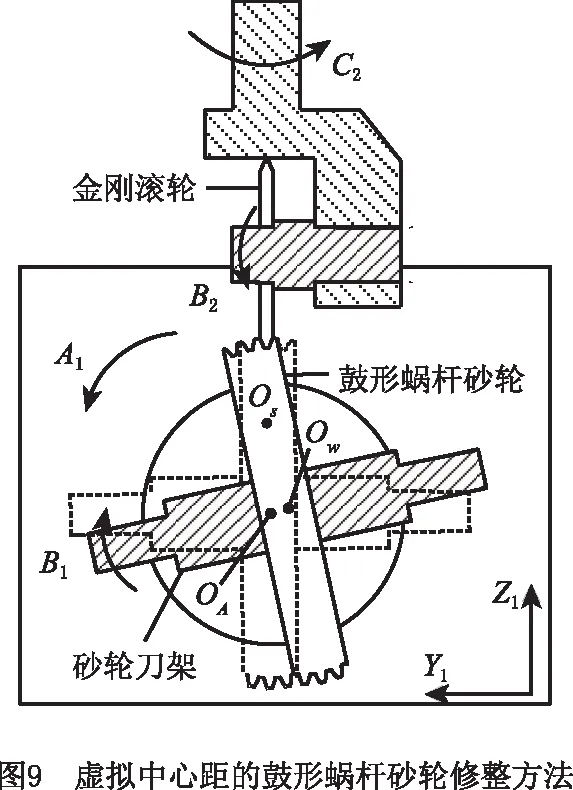
因此在修整鼓形蜗杆砂轮时,首先利用C1轴使滚轮绕竖直方向摆动一个与鼓形蜗杆砂轮名义螺旋升角相同的角度,在法截面上对砂轮进行修整;其次,控制A1,Y1,Z1,B1四轴联动,使砂轮在匀速旋转的同时相对滚轮作偏心摆动,从而修整出鼓形蜗杆螺旋面。

2.3 修整运动各轴的行程关系

基于虚拟中心距的运动分解原理,结合机床的结构和运动特性,在普通蜗杆砂轮磨齿机上修整鼓形蜗杆砂轮的运动可用图10所示的运动简图描述。以图10a中的位置为参考点,在参考点砂轮刀架水平,砂轮中心Ow与滚轮中心Od在竖直方向处于同一直线上,A1轴旋转中心OA与滚轮中心Od在水平方向存在偏距et,该偏距为常数,取决于机床结构,Os为砂轮偏摆中心。根据运动分解原理,对修整过程中砂轮在机床上的运动作如图10b所示的分解,可计算出砂轮从参考点0偏摆到任意点i时各轴的行程。

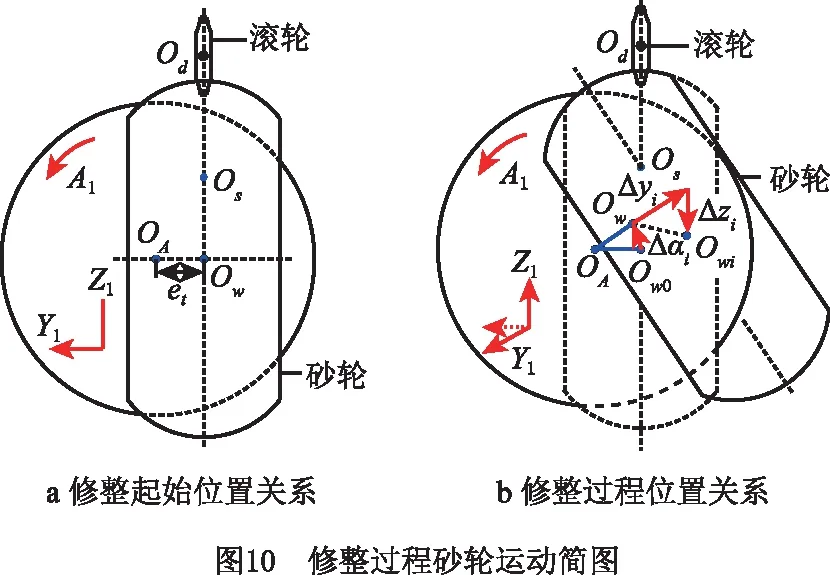
当B1轴带动蜗杆砂轮转过角度Δbi时,A1轴带动砂轮刀架旋转角度Δai,砂轮中心从Ow0到达Ow'的位置,Y1轴的方向也相应转过Δai,同时Y1轴和Z1轴分别运动Δyi和Δzi的距离,使砂轮中心到达Owi位置,值得注意的是,三轴的运动同时完成,Ow'为虚拟点,实际修整过程中砂轮中心并不会经过该点。如图10b所示,A1,Y1,Z1轴的行程与B1轴的行程之间的关系表示为:

(16)

式中:Ns为与鼓形蜗杆砂轮对应的插齿刀齿数;et为A1轴旋转中心OA与滚轮中心Od在水平方向的偏距;E为偏摆中心Os与砂轮中心Ow之间的距离。

3 鼓形蜗杆砂轮成形修整加工仿真

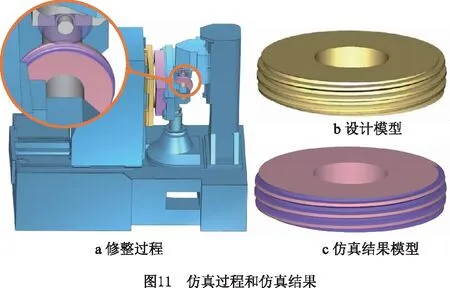
为了验证方法的正确性,利用VERICUT对所提鼓形蜗杆砂轮成形修整方法进行加工仿真。VERICUT是一款专业的数控加工仿真软件,它可以从几何角度高精度地模拟加工过程,其Auto-diff功能可比较工件仿真加工模型与设计模型之间的偏差,常用于对加工工艺和数控程序的正确性进行仿真校验[17]。

以表1所示的蜗杆砂轮设计参数为仿真实例,设计轴截面廓形与插齿刀端面截廓相同的成形金刚滚轮,搭建普通蜗杆砂轮磨齿机加工仿真模型,配置仿真控制系统为西门子840D数控系统,根据式(16)计算各轴行程并编制加工仿真程序,然后运行程序进行鼓形蜗杆砂轮修整仿真验证,修整仿真过程和结果如图11所示。

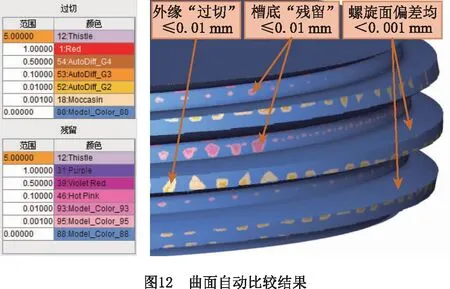
利用VERICUT的Auto-diff功能比较仿真结果与设计模型,结果如图12所示。可见仿真结果模型中,外缘部分存在“过切”,槽底部分存在“残留”,但残留和过切均不超过0.01 mm。在磨削面齿轮时,蜗杆砂轮的主要工作面为螺旋面,外缘和槽底不会对面齿轮齿面磨削精度产生影响,而由比较结果可知螺旋面上的偏差均小于0.001 mm,可以证明所提修整方法能够在普通蜗杆砂轮磨齿机上有效实现对面齿轮磨削用鼓形蜗杆砂轮的修整。

4 结束语

本文针对面齿轮的蜗杆砂轮磨削加工,研究了面齿轮磨削用鼓形蜗杆砂轮的型面计算和修整方法。主要工作如下:

(1)针对面齿轮蜗杆砂轮的型面计算方法,将面齿轮插齿刀向蜗杆砂轮演变,建立了面齿轮磨削用鼓形蜗杆砂轮的型面方程,比较了演变法与传统共轭包络法的蜗杆砂轮型面计算结果,并分析了两者的计算偏差,结果表明演变法计算精度高且能避免奇异点的限制。

(2)基于虚拟中心距加工原理,提出在普通蜗杆砂轮磨齿机上对鼓形蜗杆砂轮进行成形修整的方法,将砂轮的偏心摆动作为修整冲程运动,通过B1-A1-Y1-Z1四轴联动方式实现了对鼓形蜗杆砂轮螺旋面的修整。

(3)应用VERICUT加工仿真软件对所提鼓形蜗杆砂轮成形修整方法进行了仿真验证,结果表明所提修整方法能够在普通蜗杆砂轮磨齿机上有效修整面齿轮磨削用鼓形蜗杆砂轮,使面齿轮磨削能够在普通蜗杆磨齿机上进行,提高了磨齿机的通用性。