基于统一理论的配筋钢管混凝土柱承载力研究*

阿里甫江·夏木西, 史露江, 伊尔潘江·艾力

(1 新疆大学建筑工程学院，乌鲁木齐 830047；2 新疆财经大学国际经贸学院，乌鲁木齐 830012)

0 引言

既有研究表明钢管混凝土(concrete-filled steel tube,CFST)结构具有优越的受力性能,已被广泛应用于大型公共建筑、深海桥梁、高铁地铁建设以及工业厂房等承受巨大荷载的结构中[1],但随着城镇化的不断推进和建筑行业的迅速发展,现有的钢管混凝土结构已经不能满足人们的需求。如钢管内填充高强度混凝土时,高强度混凝土的脆性大带来的弊端还是会显现出来,因此人们开始不断探索新的结构形式。

在诸多提高延性的措施中,核心混凝土内配筋被认为较为有效[2],即形成配筋钢管混凝土(reinforced concrete-filled steel tube,简称R-CFST)。R-CFST相关研究成果[2]表明:纵筋和箍筋形成的钢筋笼会对混凝土产生二重约束作用,改善核心混凝土的不均匀性,使得核心混凝土的受力性能明显提高,同时构件的力学性能也会得到显著改善。

目前已知的R-CFST承载力计算方法的规范有美国2010年公布的规范ANSI/AISC 360-10[3]和我国2015年公布实施的《特殊钢管混凝土构件设计规程》(CECS 408∶2015)[4](简称SCFST规程)。美国规范ANSI/AISC 360-10采用叠加原理,根据既有研究[1],其计算结果过分偏保守。我国SCFST规程在《钢管混凝土结构技术规范》(GB 50936—2014)[5](简称CFST规范)给出的CFST短柱统一理论[6]公式的基础上叠加纵筋的强度给出R-CFST承载力计算公式。从统一理论的基本思路看,将纵筋的强度简单叠加显然不太合理而且有一定的不确定性,同时其结果偏保守较多[4]。

纵观既有研究[7-9],R-CFST承载力相关的计算公式均基于极限平衡理论,在现有CFST公式的基础上叠加钢筋的强度得到了R-CFST承载力计算公式,这均不符合我国基于统一理论的设计习惯。鉴于此,本文以既有试验结果为依据,首先建立R-CFST的有限元分析模型,然后在试验结果的基础上验证模型的可靠性,最后以套箍指标为主要变化参数(其中包括混凝土强度等级、钢管壁厚、纵筋直径)采用有限元分析软件ABAQUS进行大量分析,最终给出完全基于统一理论,同时匹配现有CFST规范的R-CFST短柱轴心受压承载力计算公式。

1 R-CFST的非线性有限元模型

1.1 材料模型

1.1.1 混凝土

此类构件数值分析的关键问题在于核心混凝土本构模型的确定。当前国内外学者针对CFST核心混凝土本构模型的研究比较成熟[10-14]。然而,R-CFST中钢筋对核心混凝土的受力性能产生较大影响从而使核心混凝土处于更复杂的三向受力状态。因此,既有的CFST核心混凝土本构模型不完全适合R-CFST。又因R-CFST基本受力特征与CFST相似,其核心混凝土的本构模型可在既有模型的基础上修正得到。

(1) 受压本构模型

我国的学者钟善桐[10]、韩林海[11]以及国外学者Saenz[12]、Popovics[13]、Mander等[14]已经针对约束混凝土的本构模型进行了大量的理论和试验研究。本文经过大量的试算和比较,发现Mander等提出的本构模型较为灵活、易于修正,该模型基本表达式为:

(1)

r=Ec/(Ec-Esec)

Esec=fcc/εcc

式中:σc为混凝土三向应力;fcc和εcc分别为混凝土三向应力状态下的峰值应力和对应的应变;εc为混凝土单向受压对应的应变;Ec为混凝土单向受压弹性模量;Esec为混凝土三向应力状态下峰值应力处的割线模量;r为混凝土单向受压弹性模量与混凝土单向受压弹性模量和混凝土三向受压割线模量差值的比值。

基于Richart等[15]的表达式,Mander等修正后给出:

εcc=εco[1+5(fcc/fco-1)]

(2)

式中:fl为核心混凝土三向应力状态下的侧向应力;fco和εco分别为混凝土单向应力状态下的峰值应力和对应的应变,可根据现行《混凝土结构设计规范》(GB 50010—2010)[16]确定。

式(2)中fl是整个模型的关键参数。通过试算发现,Mander等提出的本构模型中侧向应力fl不适用于R-CFST。为此,本文假设fl由两部分组成,其一是钢管施加于核心混凝土的侧向压力fsl,其二是钢筋提供的侧向压力frl,即:

fl=fsl+frl

(3)

目前针对钢筋提供的侧向应力frl没有明确的表达式。通过对R-CFST相关文献[2]查阅,发现R-CFST中纵筋是产生二重约束作用的主要因素。因此,本文将纵筋假设为埋入在核心混凝土中的二重虚拟钢管,由此按横截面面积相等原则将纵筋等效为虚拟钢管。若用ter表示虚拟钢管的壁厚,则可以得出ter的表达式如下:

(4)

式中:D和t分别为钢管外径和钢管壁厚;Asr为纵筋横截面面积。

Morino等[17]给出fsl的计算公式,在此基础上引入ter得到R-CFST的fl计算公式:

fl=0.38tfsy/(D-2t)+0.38terfry/(D-2t-2ter)

(5)

式中fsy和fry分别为钢管屈服强度和纵筋屈服强度。

(2) 受拉本构模型

现有混凝土受拉本构模型比较多。通过大量试算发现过镇海[18]的模型模拟结果与试验结果较为吻合,其受拉本构表达式为:

(6)

其中:

x=ε/εtp,εtp=65ft0.54×10-6

y=σ/ft,ft=0.26fcu2/3;α=0.312ft2;β=1.7

式中:ε为混凝土受拉应变;εtp为ft对应的应变;x为混凝土受拉应变与ft对应的应变的比值;σ为混凝土受拉应力;ft为混凝土抗拉强度;y为混凝土受拉应力与抗拉强度的比值;fcu为混凝土立方体抗压强度。

(3) 破坏准则

核心混凝土的破坏准则对计算结果影响较大。ABAQUS软件提供的混凝土破坏准则主要包括: 德鲁克-普拉格(drucker-prager,DP)准则、混凝土弥散开裂(concrete smeared cracking,CSC)准则、混凝土损伤塑性(concrete damage plasticity,CDP)准则。综合分析后发现,DP准则可适用于混凝土,但是难以定义强化阶段,同时需要修正的参数比较多,工作量比较大,对多个参数进行修正容易引起模拟结果的偏差;CSC准则低估了混凝土的塑性体积膨胀,多用于动力分析以及裂缝研究;CDP准则也可以应用于混凝土,与其他准则相比,其参数的确定较为简单、省工。依据国内外学者的研究结果和大量试算,本文采用CDP准则来定义混凝土的破坏路径。经过大量试算确定该模型关键参数:膨胀角ψ=25°、粘性参数v=0.005、双轴受压与单轴受压极限强度比fbo/fco=1.16、不变量应力比K=0.667、偏心率e=0.1。

1.1.2 钢材

目前常用的钢材本构模型有弹塑性模型、理想弹塑性模型、弹塑性应变强化模型、二次塑流模型。理想弹塑性模型既能反映实际受力状态,又能与试验结果吻合良好。因此,本文钢材本构模型选用理想弹塑性模型。

1.2 试件模型及验证

1.2.1 试件模型

试件模型的定义可以概括为以下三个方面:

(1)接触:将纵筋与箍筋合并(merge)为钢筋笼,并采用内嵌(embedded)的方式插入到核心混凝土中;混凝土与钢管之间采用面对面接触(surface to surface contact),切向接触采用罚函数(penalty contact),取摩擦系数μ=0.6,法向接触采用硬接触(hard contact);上下端刚性板与钢管和混凝土之间采用绑定(tie)接触。

(2)边界条件及加载方法:将模型底部固定,即在边界条件中设定位移转角均为零;在模型上端设置参考点,将参考点与刚性板上表面耦合;荷载施加于参考点,加载方式采用位移控制。

(3)单元类型及网格划分:单元网格的划分决定破坏模式和计算精度。本文混凝土、钢管和刚性板均为三维实体单元模型,采用八结点线性六面体单元减缩积分的C3D8R进行网格化分,网格边长确定为10mm;纵筋和箍筋采用三维线单元模型,将装配成型后的钢筋笼定义为三维桁架单元,采用两结点线性三维桁架单元T3D2进行网格化分。

1.2.2 模型的验证

为了验证本文提出的有限元模型的可靠性,基于既有的试验数据进行对比分析。试验数据来自本课题组以往的R-CFST试验结果,以套箍指标不同为原则收集的试验数据如表1所示。

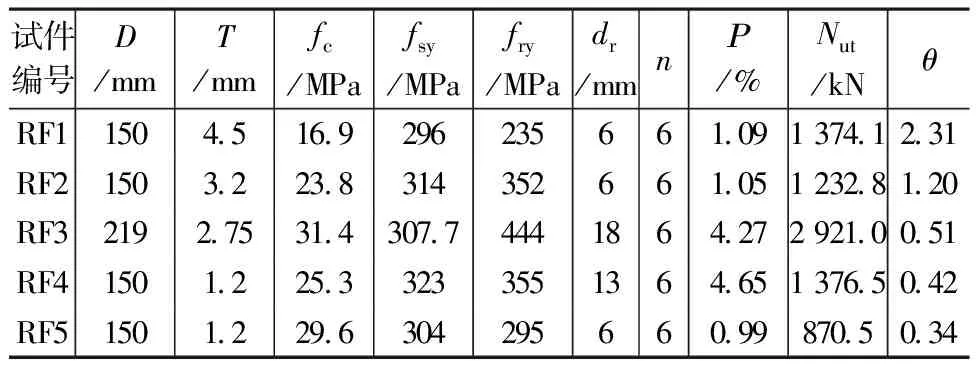
表1 试验参数

为了判别试验和模拟结果的接近程度,进行了峰值荷载差别ΔN以及试验和模拟荷载-位移曲线相关系数R2等两个方面的对比,同时将破坏模式作为参考,对比结果如图1所示。可以看出峰值荷载差别ΔN最大值为6.4%,相关系数R2最小值为0.95,破坏模式也和试验结果较为相似。可见试验与有限元模拟结果基本一致,本文提出的R-CFST有限元分析模型有效可靠。

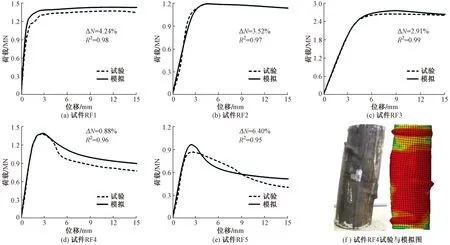
图1 试验与模拟结果对比

2 基于统一理论的R-CFST承载力分析

2.1 统一理论

统一理论在2006年由钟善桐[6]提出,即把钢管和混凝土视为统一的整体,钢管混凝土构件的工作性能随着材料的物理参数、构件几何参数和截面形式、应力状态的改变而改变,变化是连续的、相关的,而计算是统一的。在此基础上钟善桐[6]基于数值模拟方法以套箍系数为参数,提出适用于不同截面形式的CFST短柱的承载力计算公式。到2014年此理论及其计算公式被纳入CFST规范。

至于R-CFST,同理可以认为其受力响应随着混凝土强度、钢管壁厚、纵筋直径的变化而变化,变化是连续的、相关的,而计算是统一的。因此,R-CFST短柱承载力计算公式也采用与统一理论相同的方法得出。

CFST规范给出的承载力NCEST计算公式基本表达式为:

NCFST=Ascfsc

(7)

式中:Asc为CFST横截面面积;fsc为CFST组合抗压强度,即组合截面的平均压应力,与套箍系数和截面形状有关的参数。

钟善桐[6]通过观察各种状况的CFST轴心受压时平均应力与纵向应变关系曲线,并结合有限元分析认为当纵向应变为3 000με时,构件达到强度承载力极限值,此时构件开始屈服,将对应于该点的平均应力作为fsc的值,由此得出fsc的拟合经验公式。

同理,可以得出R-CFST轴心受压承载力NR-CEST基本表达式为:

NR-CFST=Ascrfscr

(8)

式中:Ascr为R-CFST横截面面积;fscr为圆形截面R-CFST的组合抗压强度,与R-CFST的套箍系数有关。

以下采用与CFST相同的思路,基于有限元分析探讨fscr的计算方法。

2.2 模型试件及参数

设计6种混凝土强度等级、6种钢管壁厚和3种纵筋直径,共108个R-CFST模型试件:试件外直径取D=165mm、高度取H=500mm;每根试件均配置6根纵筋。已有研究表明[1],箍筋间距对试件的影响较小,为了简化有限元建模过程,所有试件模型的箍筋间距d=100mm、箍筋直径dv=4mm、外环直径ds=100mm;有限元建模过程同1.2节述。

为了得到更好的模拟结果,混凝土强度、钢管和钢筋的参数均通过材性试验确定。各参数如表2所示。模拟试件的编号规则为:混凝土按照强度等级从小到大的顺序分别记为A、B、C、D、E、F;钢管壁厚按照厚度t分别记为12、23、27、32、45、60;纵筋直径分别记为6、8、10;如B-23-8代表混凝土强度等级为C30、钢管壁厚为2.3mm、纵筋直径为8mm。

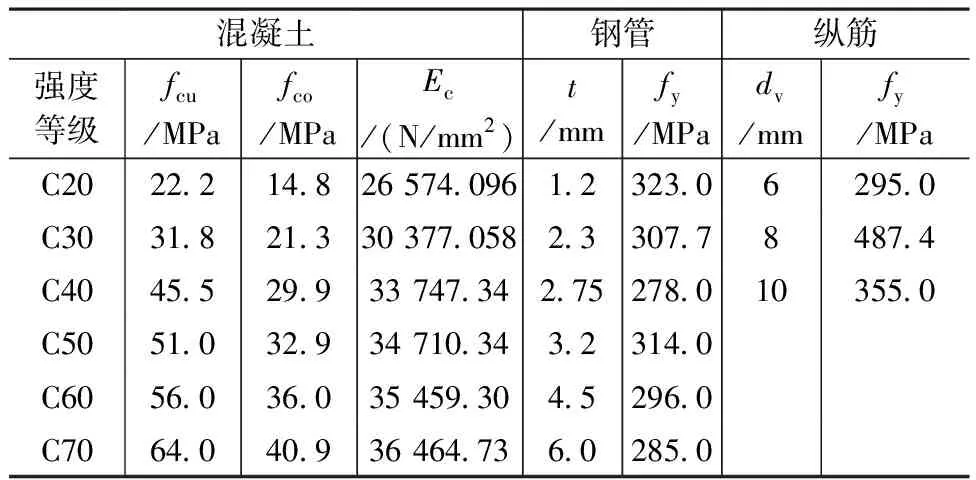
表2 材料试验结果

2.3 结果及分析

2.3.1 受力特性

通过对108个试件模型进行有限元分析,现对部分典型模型的受力特性分析如下:

图2为钢管壁厚为2.3mm、纵筋直径为8mm时,不同混凝土强度等级R-CFST的fscr与应变关系曲线。可以发现,随着混凝土强度的增大,峰值应力也随之增大,最大荷载之后塑性变形能力明显增大。

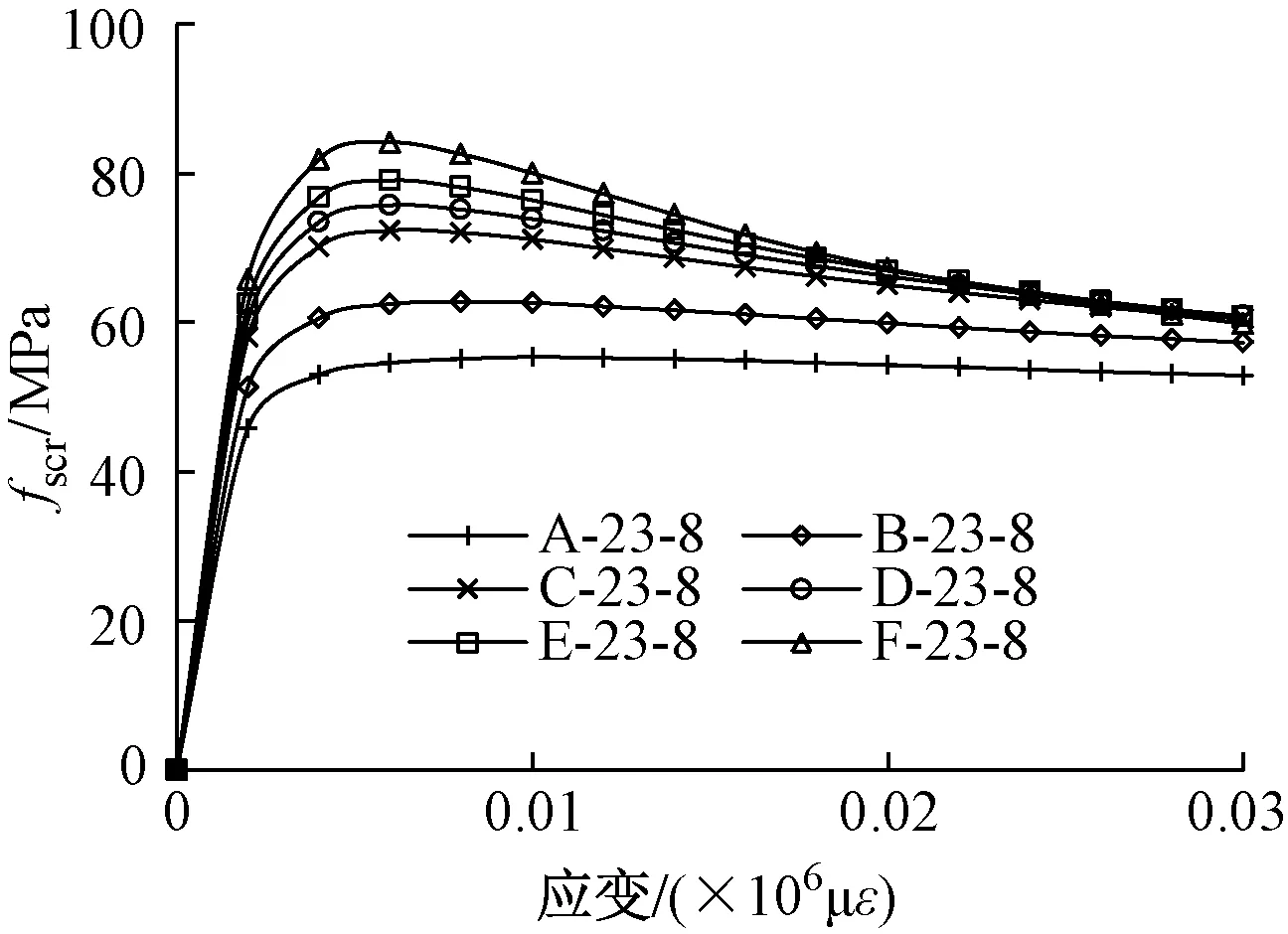
图2 不同混凝土强度等级的R-CFST的fscr与应变关系曲线

图3为混凝土强度等级为C50、纵筋直径为6mm时,不同钢管壁厚的R-CFST的fscr与应变关系曲线。可以发现,随着钢管壁厚的增大,峰值应力也随之增大,最大荷载之后的塑性变形能力明显增大。

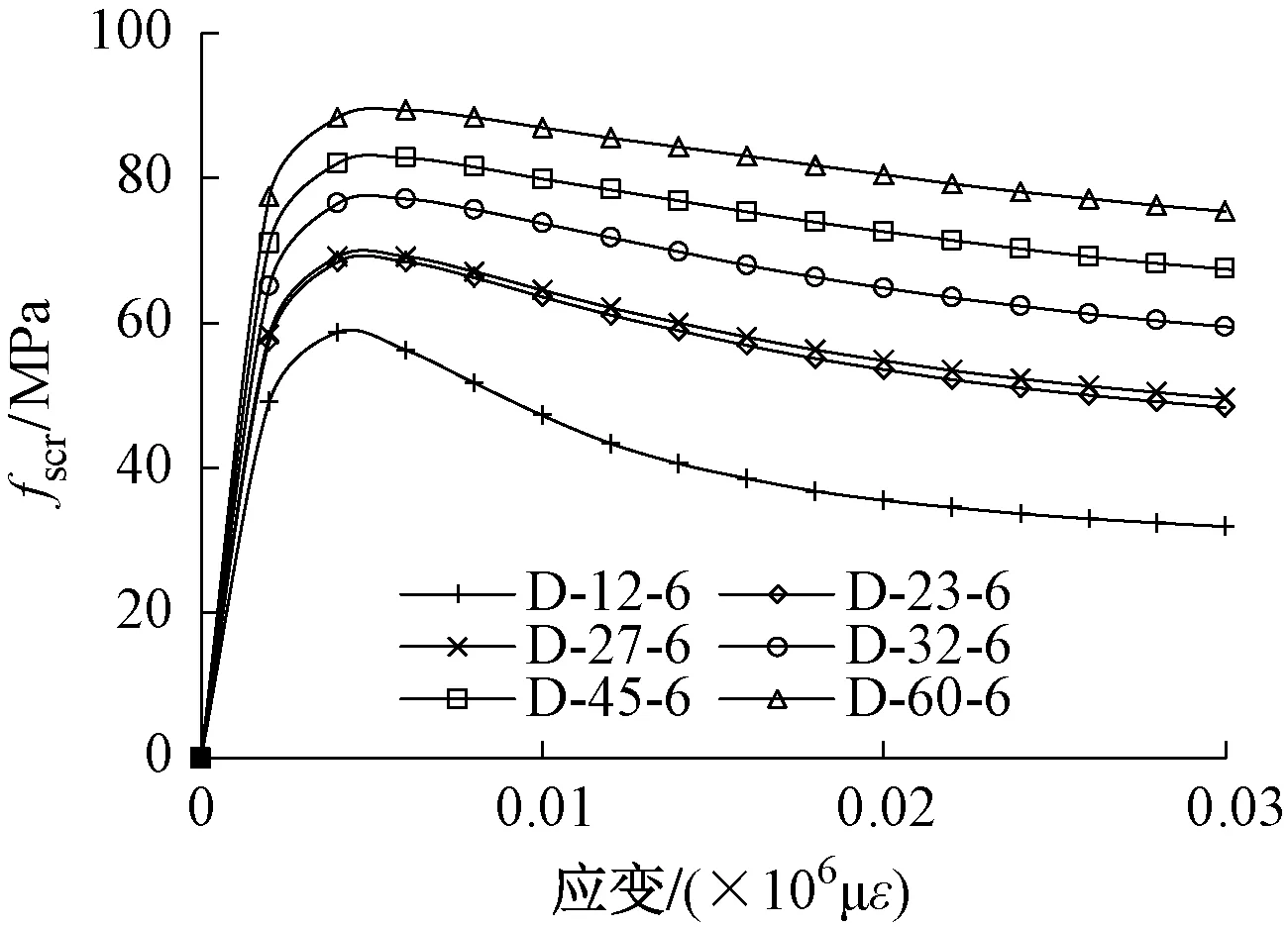
图3 不同钢管壁厚的R-CFST的fscr与应变关系曲线

图4为混凝土强度等级为C30、钢管壁厚为3.2mm时,不同纵筋直径的R-CFST的fscr与应变关系曲线。可以发现,随着纵筋直径的增大,峰值应力随之增大,最大荷载之后塑性变形能力得到提高。另外,纵筋直径为8mm和10mm时的曲线基本重合,说明在一定范围内,纵筋直径的增大可以提高试件的力学性能,但超过一定数值后,承载力的增大趋势逐渐变小。

2.3.2 R-CFST组合抗压强度计算公式

根据上述分析,混凝土强度、钢管壁厚和纵筋直径对R-CFST的承载力有明显的影响。在CFST规范给出的CFST套箍系数的基础上考虑纵筋的作用后给出R-CFST套箍系数θr的表达式:

θr=(Assfsy+Asrfry)/Accfco

(9)

式中Ass、Acc分别为钢管、核心混凝土的横截面面积。

使用式(9)计算出108个试件的套箍系数,如表3所示。可以发现,当钢管壁厚和纵筋直径相同的情况下,随着混凝土强度的增大,θr逐渐减小;当混凝土强度和纵筋直径相同的情况下,随着钢管壁厚的增大,θr逐渐增大;当混凝土强度和钢管壁厚相同的情况下,随着纵筋直径的增大,θr随之增大,增大幅度逐渐减小,说明在一定范围内,纵筋直径的增大可以提高试件的二次套箍效应。

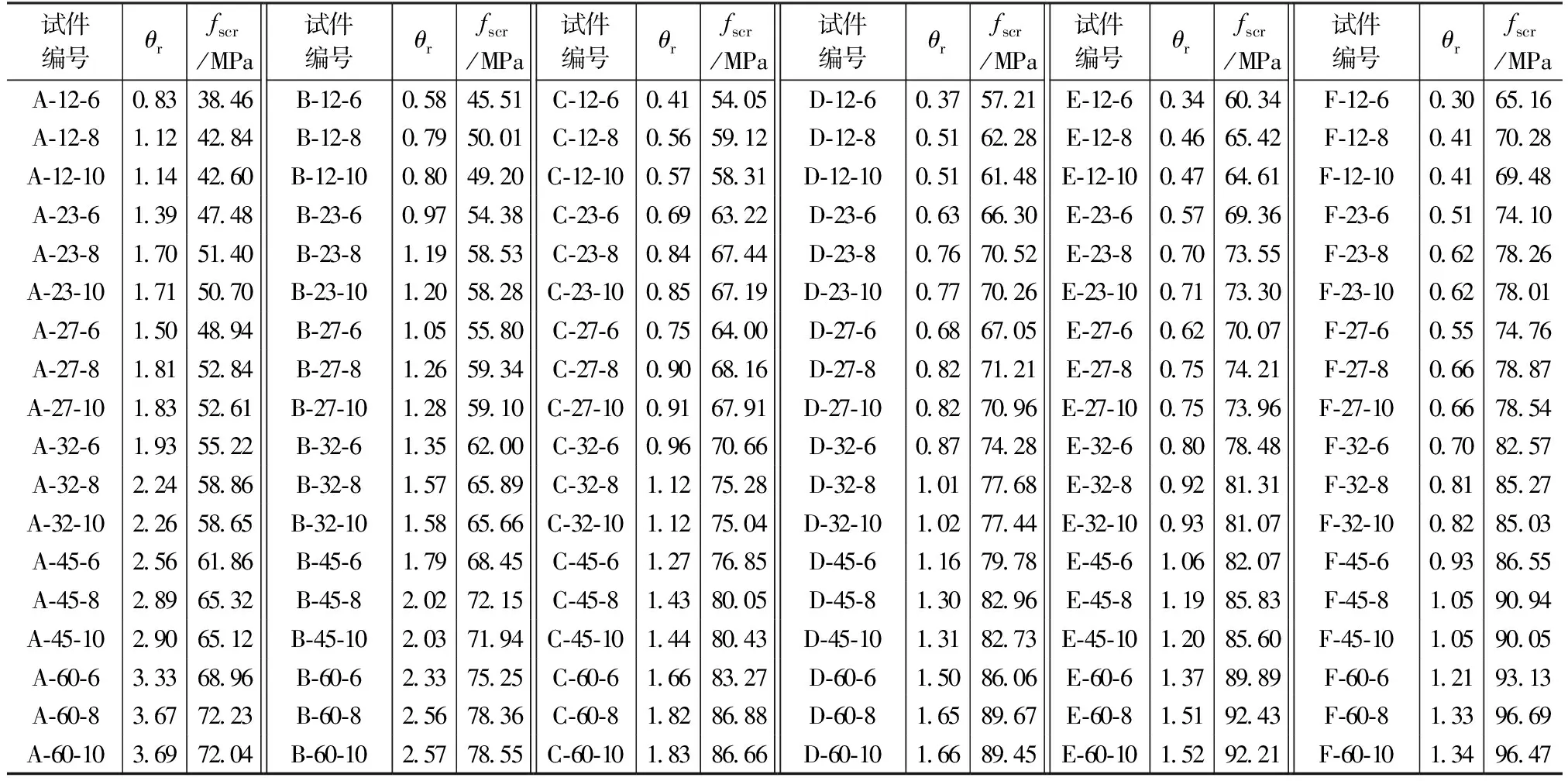
表3 模拟试件套箍系数计算值及组合抗压强度标准值

与此同时,根据fscr与应变的关系曲线,得出应变为3 000με时的fscr值,如表3所示,并将fscr/fco与θr的关系绘制成曲线如图5所示。

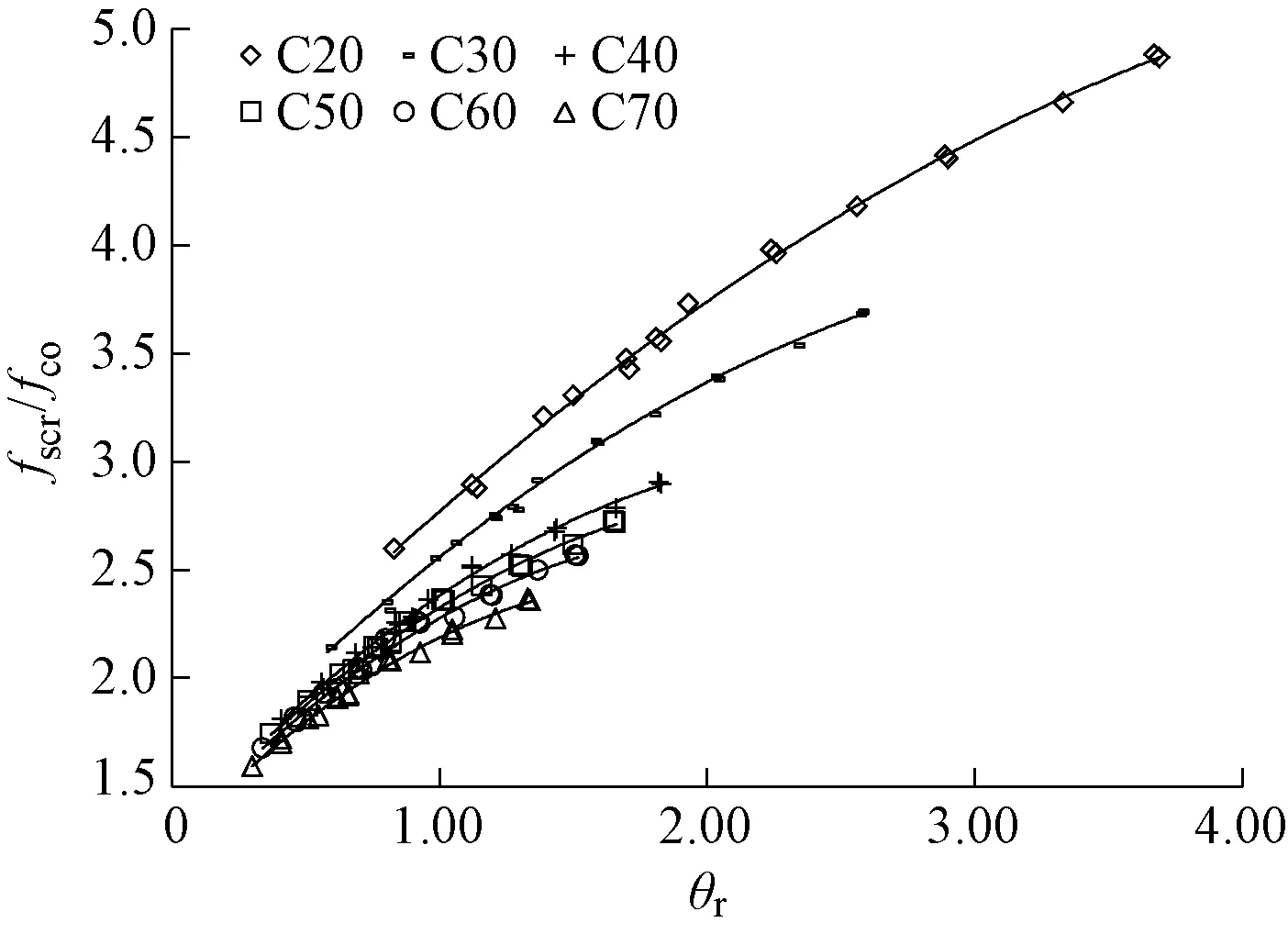
图5 fscr/fco与θr关系曲线

将fscr/fco与θr进行拟合后发现,不同混凝土强度得到的拟合曲线均为二次抛物线(图5),其拟合表达式的形式为:

(10)

再将fco与式(10)得到的6个A值进行拟合,得出拟合结果为常数1.3445;将fco与式(10)得到的6个B值进行拟合,得出拟合结果为常数1.3171;将fco与式(10)得到的6个C值进行拟合,得出拟合结果为线性变化,即C= -0.0091fco+ 0.0227。

由此可以得到R-CFST的fscr计算公式:

(11)

式(11)与CFST规范给出的fsc表达式一致,适用于圆形截面R-CFST轴心受压构件。

2.4 R-CFST承载力公式验证

为了验证本文提出的R-CFST公式的实用性,对既有试验数据进行计算分析,并与SCFST规程公式进行对比。

共收集其他文献提供的28个R-CFST轴心受压试验数据,主要参数、试验和公式计算结果列于表4,并将试验值与计算值的比值绘制于图6。SCFST规程公式,试验值与计算值比值Nut/Nu的平均值为1.06、标准偏差为0.16、最高值为1.37、最低值为0.85,最高值比最低值高出了61.18%。在所有28个数据中,试验值小于计算值占50%。

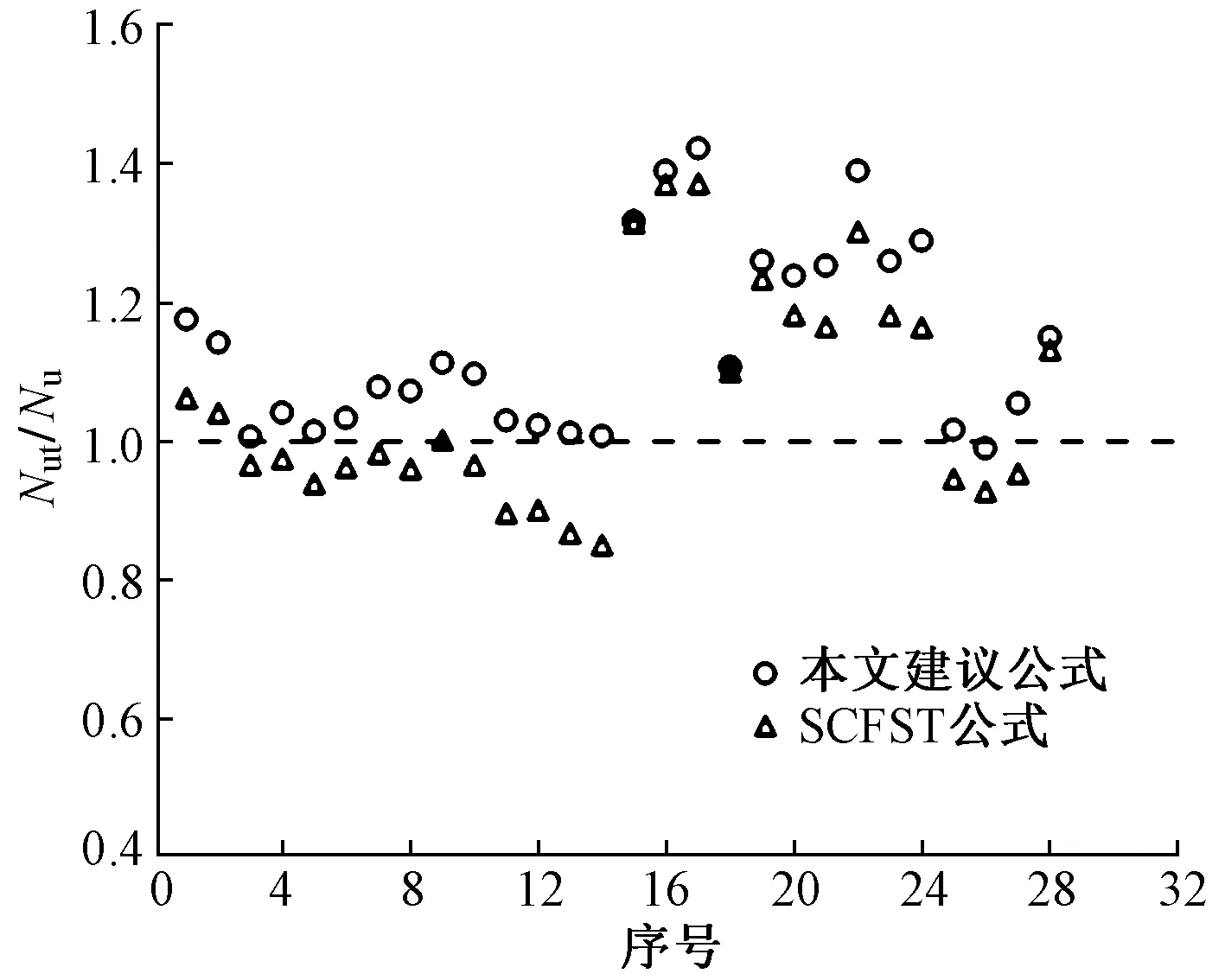
图6 公式对比分析

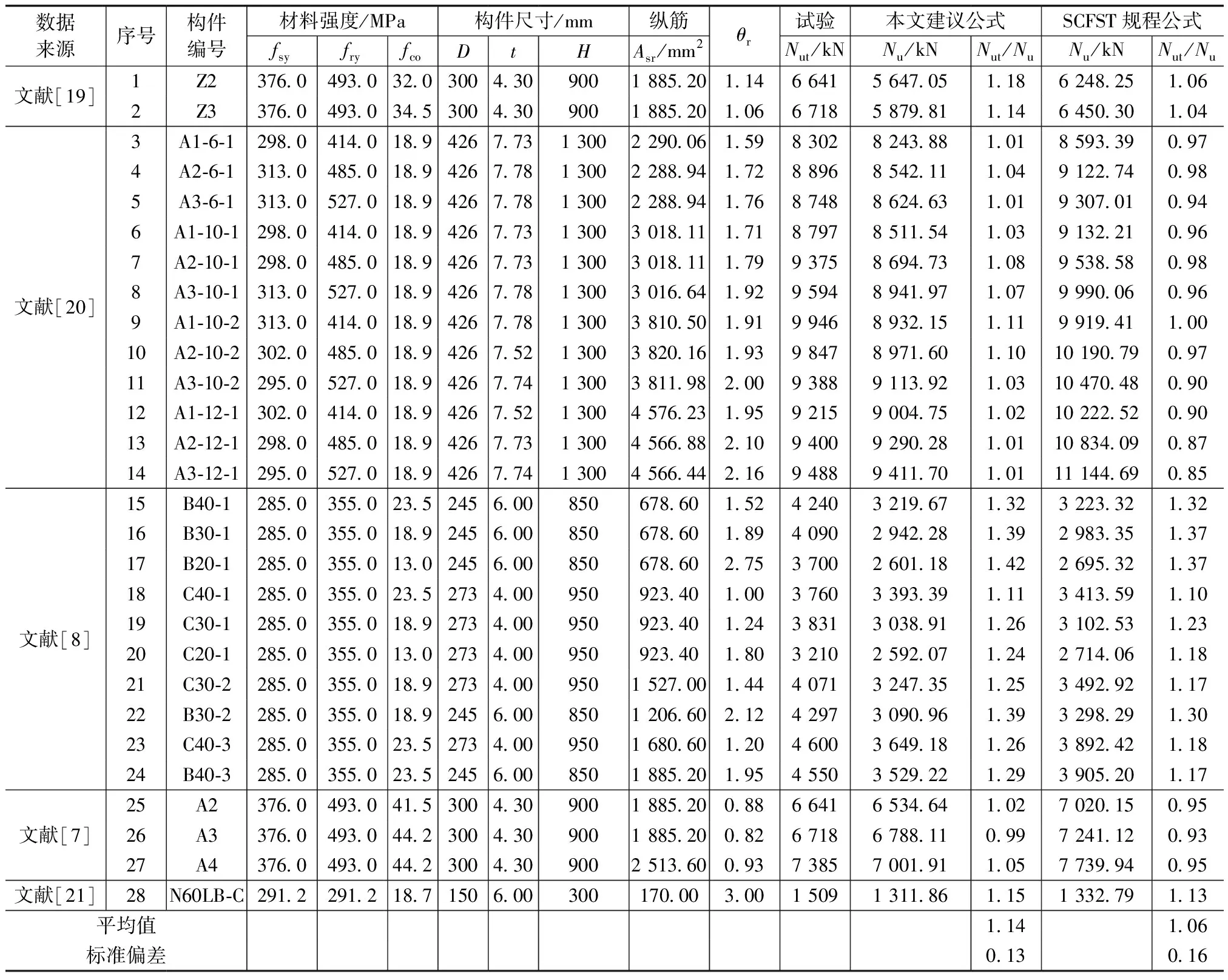
表4 试验与公式计算结果对比

本文建议公式,试验值与计算值比值Nut/Nu的平均值为1.14、标准偏差为0.13、最高值为1.42、最低值为1.01,最高值比最低值高出了40.59%。在所有28个数据中,试验值小于计算值仅有1例。由此可见,SCFST规程计算结果不符合实际情况较多,可能存在过高计算的风险;与此相比,本文推荐公式离散性较小,和实际情况更接近,计算结果稳定并安全。

3 结论

本文采用非线性数值模拟方法研究R-CFST短柱基于统一理论的承载力。主要结论如下:

(1) 建立适合R-CFST的非线性数值模拟方法。基于既有约束混凝土本构模型进行修正给出适合R-CFST核心混凝土的本构模型,并用此模型建立了模拟试件模型,然后以既有试验数据验证了分析模型的可靠性。

(2) 解释了R-CFST基于统一理论的受力性能分析方法,同时明确R-CFST具有优越的塑性变形能力。

(3) 给出适合R-CFST的统一理论承载力计算公式。以混凝土强度等级、钢管壁厚和纵筋直径为参变量定义了R-CFST的套箍指标,再以此套箍指标为参数进行了大量模拟分析,最终给出完全遵循统一理论的定义、同时匹配现有CFST规范公式的R-CFST短柱轴心受压承载力计算公式。公式的计算结果与试验结果吻合良好、离散性较小、安全、可用于工程设计。