基于流固耦合的弧形闸门-闸墩体系的流激振动研究

2023-11-13刘计良奚宏林董旭荣

水资源与水工程学报 2023年5期

刘计良, 奚宏林, 司政, 董旭荣

(1.西安理工大学水利水电学院, 陕西西安 710048; 2. 陕西省水利电力勘测设计研究院, 陕西西安 710001)

1 研究背景

弧形闸门因其可封闭孔口大、启闭力小、无门槽等优点而在水利枢纽中得到广泛应用,其通常作为工作闸门,是水利枢纽的调节结构。弧形闸门的安全运行是发挥水利枢纽综合效益的重要保障。弧形闸门在水流激励下会产生振动,当水流脉动的优势频率与闸门某一阶频率相近时就会造成共振,使闸门发生剧烈振动,并有可能失事而造成严重的损失。因此,有必要对弧形闸门的流激振动进行深入研究,以全面地对弧形闸门结构进行安全评价[1-2]。

目前对弧形闸门的流激振动已有较多研究,Erdbrink等[3]及练继建等[4]应用物理模型-数学模型联合预报方法预测了钢闸门的流激振动特性,可为实际工程提供参考;彭思贤等[5]采用数值模拟方法对大宽高比弧形闸门进行了流激振动计算和安全评估;张维杰等[6]及赵兰浩等[7]对弧形闸门进行了流激振动研究并提出了优化措施;Zhang等[8]通过对改进的弧形闸门结构进行数值分析,得出了新型弧形闸门抗振性能优于传统弧形闸门的结论,但以上对弧形闸门流激振动的研究均未考虑闸墩对闸门的影响[9]。目前因水流诱发振动而导致闸墩破坏的问题日益突出[10-12],练继建等[13]研究得出闸墩脉动压强受弧形闸门启闭状态影响较大的结论;张敏等[14]应用Ansys软件对弧形闸门及闸墩进行了三维有限元计算,根据计算结果提出了牛腿的加固措施;龚亚琦等[15]对预应力闸墩进行了流激振动研究并提出了减震措施,而上述研究中未考虑弧形闸门的流激振动对闸墩的影响[16]。

弧形闸门及闸墩在水利枢纽运行中密切相关、互相影响,形成一个体系,因此对弧形闸门-闸墩体系进行流激振动研究会更加全面。张雪才等[17]分别对弧形闸门单体和弧形闸门-闸墩体系模型进行了静、动力分析,得出了校核水位下瞬间开启工况时的弧形闸门-闸墩体系模型能合理地对弧形闸门结构进行安全评价的结论;张平[18]通过对多孔弧形闸门-闸墩的流激振动的研究,指出闸门之间的耦合作用对共用闸墩的影响大于对弧形闸门影响的结论;李火坤等[19]对弧形闸门与闸墩耦联振动系统进行了数值模拟计算,提出了避免弧形闸门振动破坏的措施。

本文在前人研究的基础上应用流固耦合理论对弧形闸门-闸墩体系进行流激振动的数值模拟研究,分析闸门及闸墩之间的相互影响关系,包括闸墩对弧形闸门自振频率、动位移及动应力的影响及弧形闸门流激振动对闸墩应力分布的影响,为弧形闸门及闸墩的安全评价提供了一种新的思路。

2 计算模型

以某水利工程弧形工作闸门为例,其闸室底板高程为326.0 m,正常蓄水位为334.5 m,校核水位为337.0 m。闸墩厚度为4.0 m、高度为25 m。闸门尺寸为 12.0 m×12.9 m(宽×高),弧形闸门支臂长15.5 m。每扇闸门共有2个主横梁、6个纵梁、14个次横梁、1个顶梁、1个底梁,采用双吊点液压启闭机启闭。

应用ANSYS建立有限元模型时,坐标系设定竖直方向为z向,垂直水流方向为x向,顺水流方向为y向。弧门属于空间薄壁结构,支铰采用solid185模拟,其他构件均采用板壳单元shell181单元模拟;闸墩选用solid185模拟。分别建立弧形闸门单体和弧形闸门-闸墩体系的有限元模型(分别称为单体模型和体系模型),如图1所示。两种有限元模型的单元数分别为23 283个和105 111个,节点数分别为21 150个和93 468个。弧形闸门两侧止水采用弹簧单元combin14模拟。水体采用三维流体声单元Fluid30模拟,模拟长度取闸门高度的3倍,其有限元模型如图2所示。

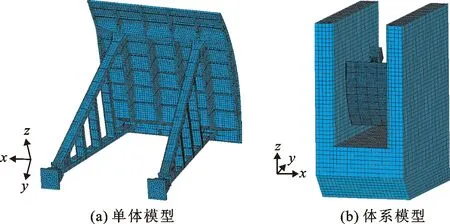
图1 弧形闸门单体和弧形闸门-闸墩体系有限元模型

图2 水体有限元模型

水体边界约束条件:水体和面板接触面标记为流固耦合接触面;底边界及顶边界施加法向约束,忽略水表面波动效应;侧边界施加法向约束来模拟无限远处的边界条件。水体密度ρ=1 000 kg/m3,声速v=1 430 m/s。

计算模型材料参数:弧形闸门为Q235B钢;支铰为铸钢ZG310—570;闸墩为C25混凝土;牛腿为C30钢筋混凝土;止水材料为橡胶。各种材料具体的力学参数见表1。

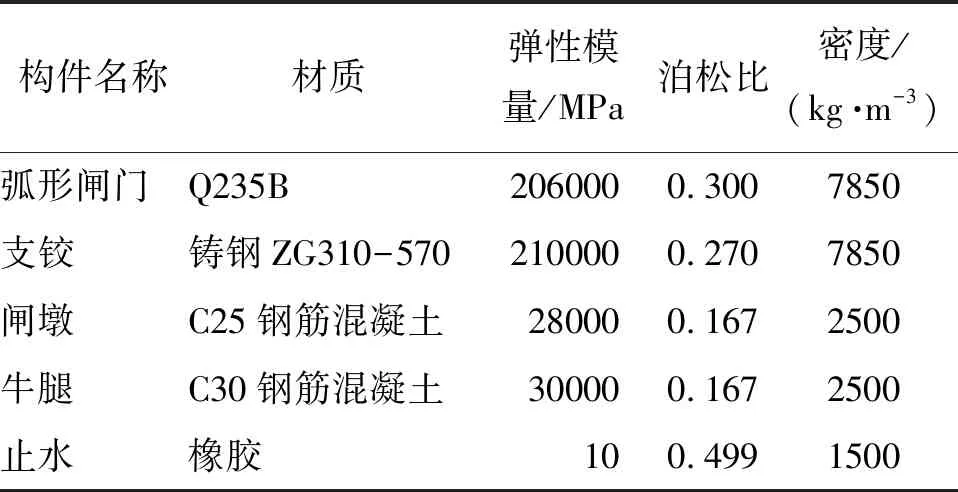
表1 各构件的物理力学参数

对该闸门进行有限元静力分析,计算闸门在设计洪水位瞬时开启工况下的应力及位移,经过计算与校核,其强度和刚度均满足设计规范要求,支臂稳定性亦满足规范要求。

3 计算理论

3.1 流固耦合自振特性分析[20]

考虑水体对闸门振动的影响建立的闸门振动系统运动微分方程为:

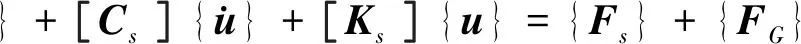
(1)

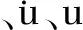
因阻尼对实际运行中的闸门振动特性的影响较小,故将公式(1)简化处理:

[Ms+Mp]{ü}+[Ks]{u}=0

(2)

由公式(2)可知,水体与结构的互相作用在动力方程中是在质量矩阵Ms的基础上附加矩阵Mp,动力方程的形式不变。对公式(2)以反幂法求解,解方程得到闸门结构的n阶频率,按从小到大顺次排列为ω1,ω2,…,ωn,即得结构的第 1,2,…,n阶固有频率[20]。

3.2 脉动水流节点荷载相关性分析[5]

假设各测点的水流脉动压力{P(t)}为平稳的各态历经随机变量,则节点荷载可表示为:

(3)

对节点荷载相关矩阵进行傅里叶转换之后的节点i,j间的节点荷载功率谱矩阵为:

(4)

其中:

(5)

假定相关函数γij为坐标的可分离函数,i、j之间相关函数γij(ω)可表示为:

(6)

(7)

A=-(Kx1(xi-xj)+Ky1(yi-yj)+Kz1(zi-zj))

(8)

B=-(Kx2(xi-xj)+Ky2(yi-yj)+Kz2(zi-zj))

(9)

将公式(5)～(7)代入公式(4)即可得到节点荷载功率谱矩阵。

4 自振特性分析

采用非对称(Unsymmetric)算法分别对单体模型和体系模型计算不同开度下弧形闸门的自振频率,并对比分析考虑流固耦合的单体模型和体系模型弧形闸门自振频率的区别。不同开度下两种模型各振动阶数自振频率及变化结果如图3所示。

图3 弧形闸门不同开度下两种模型各振动阶数自振频率及变化结果

从图3可以看出,单体模型自振频率主要集中在0～5 Hz,体系模型自振频率主要集中在0～3 Hz;在考虑闸墩的影响下,体系模型相较于单体模型弧形闸门的自振频率均有所下降,闸墩对第4阶自振频率影响最大,频率降低最大幅度为61.45%;闸墩对第2阶影响最小,频率降低最小幅度仅为0.34%。从振型角度考虑,闸墩对弧形闸门面板垂向振动影响较小,对弧形闸门面板侧向振动及支臂振动影响相对较大。考虑水体对自振频率的影响,由图3可以看出,无论是单体模型还是体系模型,随着闸门开度的增大,弧形闸门与水体接触的面积减小,弧形闸门自振频率随之增大。

通过比较弧形闸门自振频率及水流脉动压力的优势频率来判断弧形闸门是否会发生共振。闸门水流脉动压力功率谱曲线如图4所示。

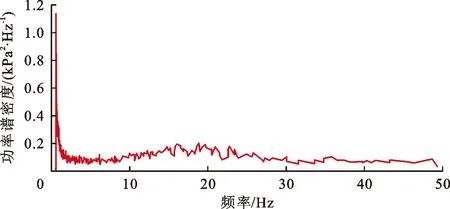
图4 闸门水流脉动压力功率谱曲线

据以往资料统计[21],超过90%以上的闸门水流脉动频率在1～20 Hz之间,其中将近50%的闸门水流脉动频率在1～10 Hz之间,47.3%的闸门水流脉动频率在10～20 Hz之间,只有极少数情况会超过20 Hz。通过比较弧型闸门的自振频率与作用水流的脉动频率主频区来评价弧门的动力稳定性,为确保弧形闸门不发生共振,应使弧门的自振频率尽量远离水流的脉动频率主频区。从图4可知,水流脉动优势频率为0.586 Hz,弧形闸门自振频率与水流脉动压力优势频率不重合,因而该弧形闸门理论上发生共振的可能性较低。但由于该弧形闸门的自振频率比较密集,且绝大多数在水流的脉动频率范围内,有必要采取相应的工程措施来防止闸门发生振动破坏。

5 动力响应分析

为进一步研究闸门结构的振动情况,根据水力学试验获得的脉动压力数据计算闸门结构的振动响应,图5为闸门某测点的水流脉动压力时程曲线。

图5 闸门某测点的水流脉动压力时程曲线

从图5可以看出,水流脉动为基本呈正态分布的平稳随机过程,水流脉动压力峰值为1.141 kPa,此测点水流紊动程度较高。

将闸门不同开度下的脉动压力作为节点荷载,通过数值模拟计算可得到单体模型及体系模型弧形闸门结构的动位移响应和动应力响应,本文主要研究体系模型的动位移及动应力。

5.1 动位移响应分析

通过数值模拟计算不同开度下两种模型弧形闸门各构件动位移响应情况,图6为体系模型相较于单体模型弧形闸门各构件顺河向最大位移变化量百分比。

图6 弧形闸门不同开度下各构件顺河向最大位移变化量百分比

模拟计算结果表明,单体模型与体系模型面板均在0.8相对开度时顺河向位移最大,主横梁及支臂均在0.6相对开度时顺河向位移最大,纵梁在0.2相对开度时顺河向位移最大;闸门相同开度下,单体模型闸门面板顺河向位移最大,纵梁次之,支臂最小,而体系模型闸门主横梁位移最小。从图6可以看出,将两种计算模型的动位移相比较,闸墩对弧形闸门面板及支臂顺河向位移的影响较大,对主横梁及纵梁顺河向位移的影响较小。考虑闸墩影响的体系模型面板顺河向位移相较于单体模型明显减小,最大减幅为44.58%;支臂顺河向位移相较于单体模型明显增加,最大增幅为37.93%;主横梁及纵梁的顺河向位移变化幅度均小于5%。

美国陆军工程师兵团(United States Army Corps of Engineers)为阿肯色河弧形闸门振动制定的允许振幅为:平均振动位移为0～0.050 8 mm时忽略不计;0.050 8～0.254 mm位移为微小振动;0.254～0.508 mm位移为中等振动;大于0.508 mm为严重振动[22]。依照此控制标准,单体模型纵梁、主横梁及支臂均属于中等振动,而单体模型面板属于严重振动;体系模型面板在0.4及0.8相对开度时属于严重振动,因此需采取工程措施减小其振动响应。

5.2 动应力响应分析

通过数值分析计算不同开度下两种模型弧形闸门的动应力响应。图7为体系模型相较于单体模型弧形闸门Mises应力变化量百分比。

图7 弧形闸门不同开度下各构件Mises应力变化量百分比

从图7可以看出,闸墩对弧形闸门支臂及面板的动应力影响较大,对其他构件影响较小。考虑闸墩影响的弧形闸门面板Mises应力有所降低,其中0.4相对开度时降幅最大,为41.70%,而支臂Mises应力均有所增加,0.2相对开度时增幅最大,为30.71%,闸墩对弧形闸门支臂的影响随着闸门开度的增加而逐渐减小。弧形闸门不同开度下主横梁Mises应力变幅均小于5%,纵梁除了在0.2相对开度之外,其余开度下Mises应力变幅也均小于5%。计算结果表明,弧形闸门在0.8相对开度时动应力响应较大,应避免在此开度过多停留。

通过数值分析计算闸墩的动应力响应,体系模型中闸墩按弧形闸门的流激振动作用进行动应力计算,计算闸墩单体模型的动应力时弧形闸门推力按《水利水电工程钢闸门设计规范》(SL 74—2019)[23]计算,动力系数为1.2[22]。图8为弧形闸门不同开度下两种模型闸墩主要受力构件牛腿x向应力值及变化量百分比。

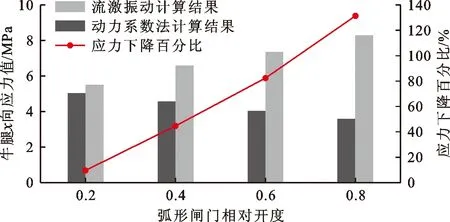
图8 弧形闸门不同开度下牛腿x向应力值及下降百分比

从图8可以看出,闸墩单体模型采用动力系数法计算时,0.2相对开度下x向拉应力最大,为5.03 MPa;体系模型按弧形闸门流激振动作用计算时,0.8相对开度下x向拉应力最大,为8.30 MPa。按动力系数法计算时,牛腿x向应力随闸门开度增加而减小,而体系模型计算的牛腿应力随闸门开度增加而增加。两种模型x向最大应力相差4.713 MPa,按弧形闸门流激振动作用进行计算时,牛腿应力较大。在0.8相对开度下闸墩应力响应最大,应避免弧形闸门在此开度过多停留,且弧门支撑结构动应力响应过大,应加强牛腿处的配筋。

6 讨论

目前对弧形闸门及闸墩的流激振动的研究以物理模型和数值模拟为主,大量学者将数值模拟计算的结果与物理模型实测结果进行了对比,发现数值模拟计算结果与实测值相差不大。因而,数值模拟结果可以有效地对弧形闸门及闸墩的动力安全性进行评估[24]。

弧形闸门及闸墩联系紧密,互相影响,形成一个体系,因此对弧形闸门-闸墩体系模型进行流激振动研究会更加全面。以往多数研究未充分考虑闸门和闸墩之间的相互影响关系[25],如今许多学者已经意识到有必要将弧形闸门与闸墩作为一个体系进行流激振动研究,以便更加合理地评估结构的动力安全性[9,17-18]。应用数值模拟对弧形闸门-闸墩体系进行研究,分析闸墩对弧形闸门的影响规律,其结果可为弧形闸门的安全评价提供参考。本文建立了弧形闸门-闸墩体系的三维有限元模型,研究闸门和闸墩在动力特性及流激振动响应方面的相互影响关系,包括闸墩对弧形闸门动力特性的影响及二者流激振动的相互影响,弧形闸门-闸墩体系模型可以更真实地反映闸门及闸墩的振动情况。但本文未考虑弧形闸门连续启闭工况,因此后续会在此次研究基础上对弧形闸门-闸墩体系模型在弧形闸门开启及关闭过程中的流激振动进行研究,以便更全面地对弧形闸门及闸墩进行安全评价。