梯级水库群多目标协同均衡调控研究
2023-11-13金文婷王义民王学斌畅建霞肖薇薇
金文婷, 王义民, 王学斌, 畅建霞, 肖薇薇
(1.安康学院 旅游与资源环境学院,陕西 安康 725000; 2.省部共建西北旱区生态水利国家重点实验室(西安理工大学), 陕西 西安 710048)
1 研究背景
梯级水库群承担着防洪、供水、发电、生态、航运等多重任务,多目标之间往往存在矛盾竞争关系,需要通过水库群多目标优化调度来实现多用水过程的统一与综合效益发挥[1-2]。传统的梯级水库多目标优化调度方法通常采用权重法或约束法将多目标问题转化为单目标问题,或采用多目标智能进化算法直接求解[3-4],而对如何实现水库群调度过程中多目标利益的协同与均衡保障研究不足,尚未形成水库群多目标协同均衡调控的理论与方法。此外,传统的水库群多目标优化调度往往追寻多目标的总利益值最优,如调度期内总发电量最大、总缺水量最小等,对各目标用水过程中的某些关键时期或关键指标(统称为“关键利益”)的关注度不够。多目标的关键利益与经济社会发展、河流生态健康的用水根本密切相关,一旦关键利益受到较大损失,将对区域经济和生态环境带来重大影响。高维、非线性、动态开放的水库群多目标调度系统具有非线性动态系统所特有的混沌特征,梯级水库群多目标协同均衡调控应与降低调度系统的混沌特征紧密相联。因此,在有限的水资源条件下,对存在多目标竞争关系的梯级水库群进行多目标协同均衡调控,优先保障关键利益,实现梯级水库群调度下多目标在时段间形成协同有序、在时段内达到利益均衡,并引导梯级水库群调度系统向降低混沌特征的方向演进,是本研究的主要目标。
协同学是研究开放系统通过内部子系统间的协同作用促使大系统从无序向有序结构转变的理论,已被广泛应用到了水资源研究领域[5]。2018年,申晓晶[6]解析了水资源协同配置的定义与基本内涵,并实现了基于协同论的水资源配置模型构建及应用;2020年,Zhang等[7]基于协同理论和信息熵建立了水-能源-粮食复合系统协同度评价模型,并采用改进的遗传算法对模型进行求解;2023年,何中政等[8]基于协同学提出了考虑时间序列特征的水资源耦合系统有序度评价方法,提升了协同学有序度评价方法在水资源系统综合评价方面应用的普适性;同年,陈文龙等[9]提出了大湾区水安全协同调控理论,构建了5个水安全调控子系统,并探讨了各子系统间的协同作用原理、协同调控的关键技术需求及协同调控模型算法等。混沌是指具有确定性的动力学系统受到非线性变量的影响而产生的一种没有规律又貌似有规律的现象,是非线性动态系统所特有的一种运动形式[10]。国内外学者将混沌理论应用于梯级水库群多目标优化调度问题时,多为借助混沌序列良好的随机性和遍历性,采用混沌映射的方式初始化进化算法种群,以应对进化算法随机生成初始种群所存在的缺陷,如个体质量较差、局部收敛早熟等。如:2016年,邹强等[11]从利用混沌思想初始化种群、构建自适应激活机制和精英粒子混沌局部搜索策略3个方面对量子粒子群算法进行了改进,通过在梯级水库群防洪优化调度中的应用,证明了所提方法收敛速率快、求解精度高;2018年,Feng等[12]提出了一种并行多目标遗传算法,依据混沌理论初始化种群规模,并将初始种群分解为多个子种群,采用并行计算同时进化多个子种群,提高了个体解的可行性和收敛速度;2021年,Su等[13]提出了一种多目标改进混沌蝙蝠算法,该算法利用混沌理论生成初始种群,通过更新映射速率提高种群多样性,且设计了自适应更新机制控制收敛速度,并将该方法应用于考虑发电和生态的多目标梯级水库群优化调度中。2023年,Basu等[14]提出了一种快速收敛的实编码遗传算法,并利用混沌映射在置信区间内生成初始种群,应用于制定由抽水蓄能电站、太阳能光伏电站和风力发电机组组成的能源系统短期最优发电计划。不同于以往研究,本文将侧重于识别和量化梯级水库群多目标调度系统自身的混沌特征,并运用均衡调控的方法引导水库群复杂调度系统降低其混沌特征,同时实现多目标协同均衡。
本文对多目标水资源利用的关键利益与非关键利益进行识别及序参量选取,基于协同学提出了梯级水库群多目标协同控制理论并构建了多目标协同优化调度模型;在通过多目标调度实现时段间协同有序的基础上,提出了基于满意边界的时段内多目标利益均衡调控方法;并引入混沌时间序列分析方法中的关联维数及Kolmogorov熵识别水库群多目标调度系统的混沌特征,以混沌特征是否减小作为评价多目标利益均衡调控是否可行的依据,引导水库群多目标调度系统向降低混沌程度及复杂程度的方向演进。将所提理论与方法应用到黄河上游梯级水库群多目标优化调度中,以验证其可行性与合理性。
2 基于协同学的梯级水库群多目标协同优化调度
协同学是由德国物理学家赫尔曼·哈肯(Hermann Haken)于20 世纪 70 年代创建的一门跨越自然和社会科学的交叉学科。根据协同学理论,复杂开放系统处于相变点的变量可分为快变量和慢变量两类,慢变量是决定系统相变的根本变量,又称为序参量,支配着子系统的行为;快变量服从于慢变量,对系统的结构、功能变化不起主导作用[15]。可见,复杂开放系统由无序走向有序的关键在于子系统内部序参量间的协同作用。
对于梯级水库群多目标调度系统而言,若将每一个用水目标视为一个子系统,则科学识别各目标子系统的关键利益与非关键利益序参量,并促使各子系统序参量间的协同有序是实现梯级水库群多目标协同优化调度的关键。梯级水库群多目标调度的关键利益,是指各用水目标中涉及特殊或重要价值的用水需求,一旦不能满足将对该目标效益造成严重不利影响的指标;非关键利益是指各用水目标中非刚性需求的利益,当遭到适度破坏时不会对目标子系统造成严重影响的弹性利益。存在激烈竞争关系的梯级水库群多目标优化调度过程中,应优先保障各目标的关键利益,其次适度满足非关键利益,缓解多目标之间的矛盾竞争关系。因此,可在识别各目标子系统的关键利益与非关键利益序参量的基础上,构建以多目标总协同度最大为目标的梯级水库群多目标协同优化调度模型,以实现梯级水库群多目标协同优化调度。关于梯级水库群多目标协同控制原理、多目标之间的协同控制原则、多目标关键利益与非关键利益序参量的选取及阈值确定、序参量及子系统有序度的计算方法、水库群多目标协同优化调度模型构建并求解,以及模型的有效性、合理性等可参考文献[16]。
3 梯级水库群多目标均衡调控
3.1 基于满意边界的时段内多目标利益均衡调控
通过梯级水库群多目标协同优化调度,可以获得不同时段水库群的调度方案及各目标的协同情况,为确保多目标在时段内达到利益均衡,本节主要介绍基于满意边界的时段内多目标均衡调控。目标满意度一般指目标利益的获得值与期望值的比值,是介于0~1之间的数值。对于梯级水库群多目标调度而言,可选择时段缺水量、时段发电量、生态流量及调沙流量分别作为供水、发电、生态、输沙目标的利益值,并由公式(1)计算满意度[17]。由各目标满意度的最大、最小值所构成的区间即称为多目标的满意边界,若梯级水库群多目标协同优化调度结果中某一时段有目标的满意度不在满意边界内,则称该时段为满意边界破坏点,需要对该时段进行多目标利益均衡调控。
(1)
式中:t为时段;xt为t时段的目标利益获得值; maxxt为t时段的目标利益期望值,生态、输沙目标的时段利益期望值可设置为需求生态流量及调沙流量的最大值,供水、发电目标的时段利益期望值可设置为长系列多目标协同优化调度结果中时段缺水量、时段发电量的最大值;M(xt)为t时段的目标满意度;发电、生态、输沙目标的满意度计算适用于当M(xt) 的取值与xt的值成正比时,即M∝xt,供水目标的满意度计算适用于M(xt) 的取值与xt的值成反比时(时段缺水量越大,满意度越低),即M∝1/xt。
合理地确定多目标利益的满意边界,是实现时段内多目标利益均衡调控的前提。多目标利益满意边界确定方法可分为直接确定和间接确定两类。如在生态和输沙目标中,时段生态流量与调沙流量均有最大、最小值限制,若不满足该限制要求,则无法保障河流基本的生态健康功能及泥沙输移功能。因此,生态、输沙目标逐时段满意边界可直接由生态流量及调沙流量的最大、最小值与期望值的比值得到。由于以供水和发电目标无法直接确定逐时段缺水量及梯级发电量的最大、最小值,可通过对梯级水库群长系列单目标调度结果进行分析,间接确定逐时段满意边界。具体方法为:构建兼顾其他用水需求的供水或发电单目标优化调度模型,以长系列径流资料驱动模型求解,根据模型结果统计多个水文年的年内逐时段单目标利益落值区间,并根据公式(1)计算目标利益满意度,由多个水文年目标利益满意度的上、下包线得到该目标逐时段的满意边界。受篇幅所限,供水、发电单目标优化模型的构建及求解过程不再列出。
图1为由单一时段内多目标满意度构成的平面坐标系。由图1可以看出,多目标满意边界(坐标轴中黑色实线矩形框区域)内各目标的满意度越高,则多目标的满意度值在平面坐标系中相互连线所形成的闭合面积越大,体现了该时段多目标利益满足状态越好;相反,各目标满意度越小,则在平面坐标中所形成的闭合面积越小,反映出该时段多目标利益满足状态越差。因此,可由时段内多目标满意度的闭合面积(简称“满意面积”)来反映该时段的多目标利益满足状态。

图1 单一时段内多目标利益均衡调控示意图
以某一时段的多目标利益均衡调控为例:若某些目标的满意度不在满意边界内(即出现满意边界破坏点),则对该时段多目标进行均衡调控,使得多目标在满足满意边界约束的情况下最大化满意面积。以供水、发电、生态、输沙4个目标为例,构建时段内多目标利益均衡调控模型,具体数学表达式如下:
(1)目标函数(时段内多目标满意面积最大):
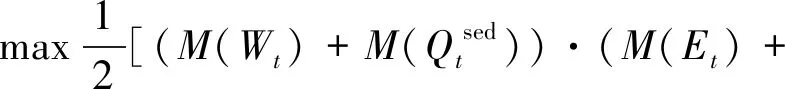
M(Qteco))]
(2)
式中:Ut为t时段的多目标满意面积;M(Wt)、M(Qtsed)、M(Et) 、M(Qteco) 分别为t时段的供水满意度、输沙满意度、发电满意度、生态满意度。
(2)约束条件:
Mmin(xt)≤M(xt)≤Mmax(xt)
(3)
式中:M(xt)为t时段的目标满意度;Mmax(xt)与Mmin(xt)分别为该目标t时段满意度的最大、最小值,即满意边界。
3.2 梯级水库群调度系统混沌特征识别与引导
针对多目标利益均衡调控前、后水库群多目标调度系统的混沌特征有何变化以及如何引导梯级水库群减小自身的混沌特征等问题,本节提出了梯级水库群调度系统混沌特征的识别与引导方法。由于梯级水库群多目标调度系统具有动态开放、高维非线性、组织复杂等特点,其资源输入与规划、获取评价和共享集成等环节易受不确定因素的影响。因此,判定梯级水库群多目标调度系统为非线性动态系统,具有混沌特征。混沌理论中的分形维数是定量刻画非线性系统混沌特征的重要参数,而分形维数中的关联维数能够定量描述系统结构的复杂程度[18];熵理论中的Kolmogorov熵(以下简称K熵)作为刻画非线性动态系统的重要特征量,能有效度量系统的混沌程度[19]。关联维数越小,表明非线性动态系统的层次越高,复杂度越低,趋势越显著;K熵的取值越大则表明系统混沌程度越大,系统越复杂。因此,可以将梯级水库群多目标调度系统的关联维数及K熵是否减小作为评判多目标利益均衡调控是否合理可行的依据,引导水库群调度系统向降低混沌程度的方向演进。
识别非线性动态系统的混沌特征,首先需要提取能够反映系统运行状态的混沌时间序列。由3.1节的分析可知,梯级水库群调度系统运行状态的实质是逐时段多目标利益满足状态时间序列的综合表现,则梯级水库群调度系统的运行状态就可以用逐时段多目标满意面积的时间序列{U1,U2,…,Ut}来表示。梯级水库群调度系统混沌特征识别与引导流程为:(1)将协同控制模型求解得到的长系列水库群运行方案作为初始方案,计算初始方案逐时段的多目标满意度及满意面积;(2)依照参考文献[18]、[19]的方法计算初始方案多目标满意面积时间序列的关联维数和K熵,分别记作D0、K0;(3)基于满意边界对初始方案进行逐时段多目标利益检验,若有满意边界破坏点则进行时段内多目标利益均衡调控;(4)均衡调控有可能使得原初始方案中该时段后的水库运行过程不再满足水量平衡条件,则保持该时段及其前所有时段的水库群运行过程不变,从下一时段开始重新寻求多目标总协同度最大的水库群运行方案,称为“调控方案1”,并计算调控方案1的关联维数及K熵,分别记作D1、K1;(5)判断D1、K1是否小于D0、K0,若小于则说明均衡调控措施减少了调度系统的混沌程度,否则取消该次对满意边界破坏点的均衡调控;(6)对调控方案1继续寻找满意边界破坏点,从步骤(3)开始重复上述过程,直至遍历所有时段。梯级水库群多目标协同优化调度研究流程如图2所示。
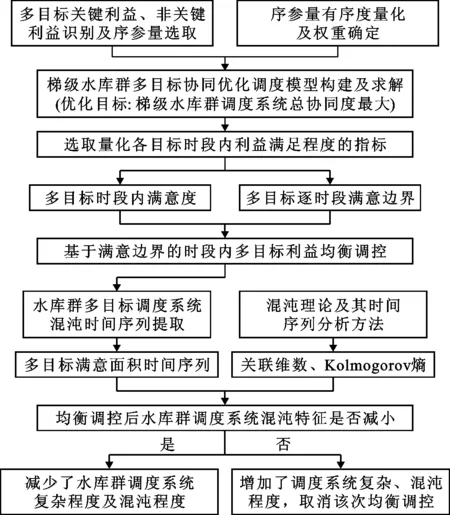
图2 梯级水库群多目标协同优化调度研究流程
4 研究实例与相关资料
4.1 黄河上游水库群概况及资料
黄河上游是指内蒙古自治区的托克托县河口镇以上河段,上游全长3 472 km,总落差3 494 m,径流量占黄河全年径流总量的60%以上。目前,黄河上游具有较大调节能力的梯级水库为龙羊峡水库(多年调节)和刘家峡水库(年调节),这两个水库承担着黄河上游防洪、防凌、供水、发电、输沙、生态等多重任务,为本文的研究对象。此外,还建有拉西瓦、尼那、李家峡、积石峡、直岗拉卡、杨康、公伯峡、苏只、盐锅峡、八盘峡、小峡、大峡、青铜峡等13座水电站,可视为径流式电站。本文构建的黄河上游梯级水库群多目标协同优化调度模型中,将防洪、防凌目标转化为约束条件进行控制,将供水、发电、输沙、生态4个目标作为水库群协同优化的多目标。
来水资料方面,收集到了黄河上游唐乃亥水文站、龙羊峡至刘家峡区间、刘家峡至兰州区间的1990年7月—2015年6月的逐月径流资料;多目标需水方面,兰州断面为黄河上游满足供水需求的主要控制断面,兰州断面逐月所需的河道外农业及工业、生活、生态综合用水量如图3所示。
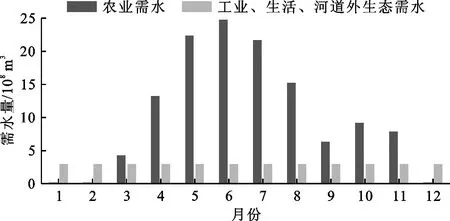
图3 黄河上游兰州断面河道外逐月综合需水过程
黄河上游防洪、防凌对象主要为沿黄城市及宁蒙河段,每年11月至次年的3月为防凌期,该时期逐月防凌控制流量分别为731、480、439、383、421 m3/s;基于已有的维持黄河干流水生态系统良性循环的重要断面生态需水成果[20],本文考虑黄河上游石嘴山及头道拐断面的生态需水过程及生态脉冲需求,如表1所示。参考黄河上游梯级水库调水调沙已有成果[21],设置调水调沙的控制流量阈值为2 240~3 000 m3/s,调沙历时为10~30 d,调沙时机为7月中旬至8月下旬支流高含沙洪水期。
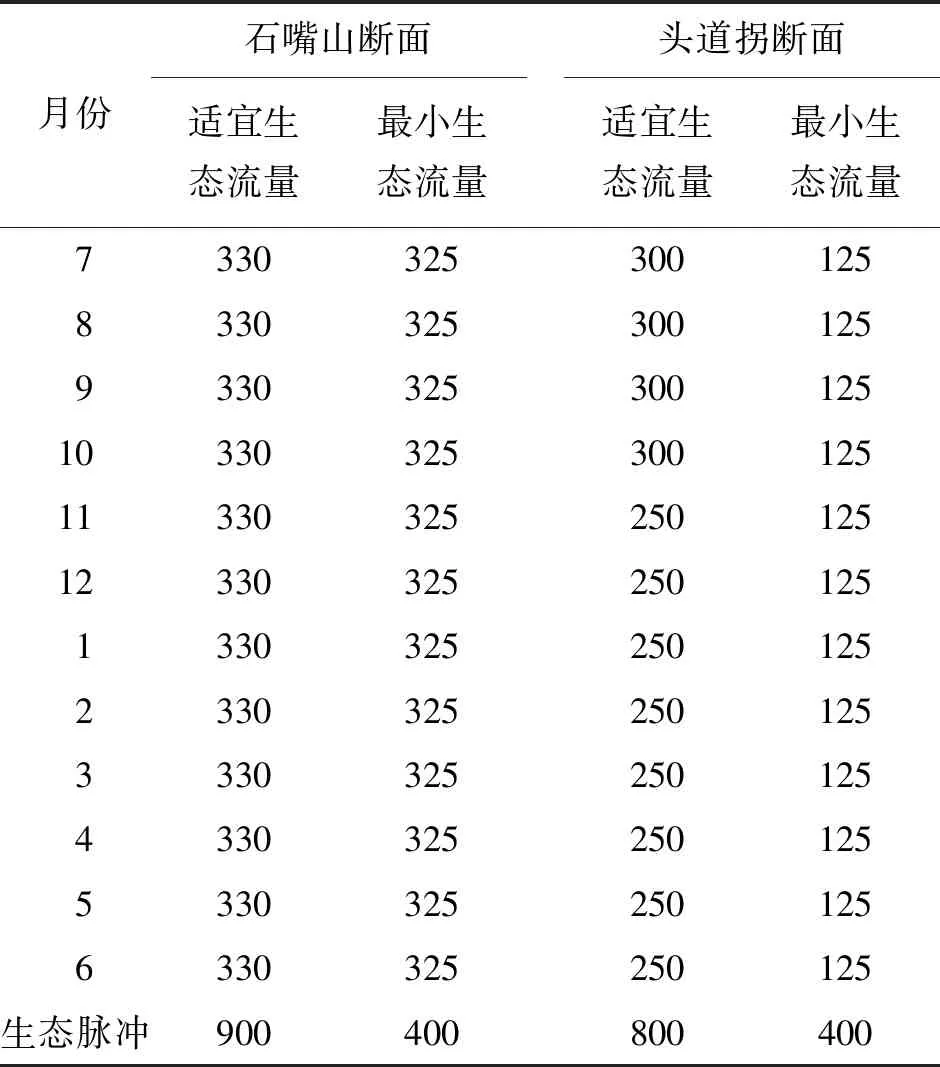
表1 黄河上游石嘴山、头道拐断面生态需水过程 m3/s
4.2 黄河上游多目标关键利益与非关键利益识别及其序参量选取
根据用水目标关键利益与非关键利益的内涵识别黄河上游供水、发电、生态、输沙多目标的关键利益与非关键利益,并提取相应的序参量。例如,供水目标中,工业、生活及河道外生态需水(统称为“河道外非农业用水”)是保障经济社会发展与人民群众生活水平的重要资源,应视为关键利益;农业用水中,农作物生长周期中对水分敏感且与产量密切相关的某些重要阶段(如玉米的抽雄期、开花期,小麦的拔节、灌浆期等)的灌溉用水应视为关键利益;生态目标中,河道内生态基流的保障能力及鱼类繁殖生长所需的每年至少1次生态脉冲为关键利益;发电目标中,非防凌期(4—10月)的梯级水库群发电效益为关键利益;输沙目标中,与1次调水调沙输沙效果直接相关的是调沙控制流量与调沙时长这两个指标,应视为关键利益。结合黄河上游宁蒙灌区的作物种植结构及主要作物生育期重要阶段的时间分布特点,确定5月上旬和中旬、6月上旬、7月上旬和中旬及8月中旬为灌溉用水的关键时期(以下称“农业关键期”)。表2列出了黄河上游多目标用水的关键利益与非关键利益序参量。

表2 黄河上游梯级水库群多目标关键利益与非关键利益序参量
4.3 序参量权重
为了确保序参量权重系数的科学性和有效性,本文通过邀请10位专家对黄河上游多目标序参量的相对重要性进行两两比较,建立成对比较判断矩阵,采用层次分析法(analytic hierarchy process,AHP)求解序参量权重,结果如表3所示。表3中4个子系统判断矩阵的一致率指标CR均小于0.1,通过了一致性检验,表明所得权重科学、合理。
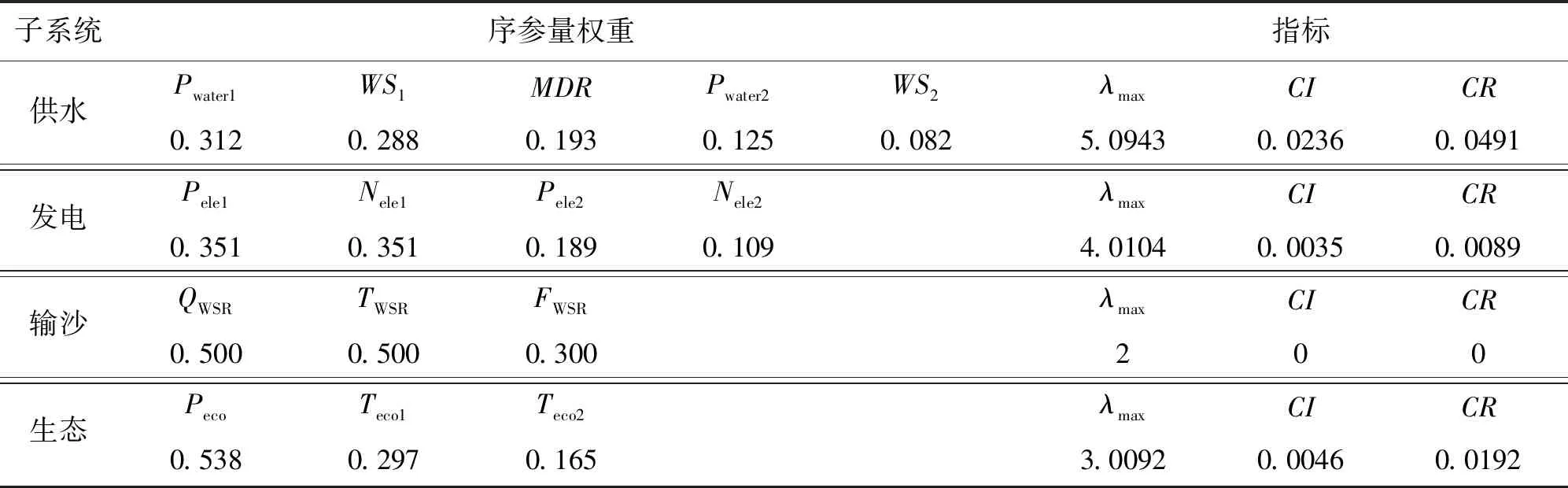
表3 黄河上游梯级水库群多目标各子系统序参量权重
4.4 黄河上游梯级水库群多目标满意边界
黄河上游梯级水库群生态与输沙目标的满意边界由时段生态流量与调沙流量需求的最大、最小值与期望值的比值所对应的满意度确定;供水、发电目标的满意边界由兼顾其他用水需求的供水或发电单目标优化调度模型结果确定。图4为黄河上游梯级水库群调度下供水、发电目标长系列多个水文年的满意度落值区间,以多年逐时段的满意度上、下包线作为满意边界。

图4 黄河上游梯级水库群不同水文年供水、发电目标逐时段满意边界
5 结果分析
5.1 多目标均衡调控与混沌特征识别过程
将径流资料、需水资料输入黄河上游梯级水库群多目标协同优化调度模型中进行求解,得到初始方案,并提取初始方案的梯级水库群多目标满意面积时间序列,计算初始方案的关联维数和K熵(D0、K0);通过对初始方案进行逐时段多目标利益均衡检验,其中2008年7下旬的供水目标满意度不在满意边界内,对该时段进行利益均衡调控,并从下一时段开始重新寻求“水-沙-电-生态”总协同度最大的水库群运行方案,称为“调控方案1”,计算调控方案1的关联维数和K熵(D1、K1),结果表明D1

表4 初始方案、调控方案1、调控方案2的特征指标值
由表4可知,初始方案的多目标总协同度为0.64;对初始方案的多目标满意度闭合面积时间序列混沌特征识别过程中,相空间重构的延迟时间为2,嵌入维数增加到17时达到稳定,此时初始方案的关联维数及K熵分别为4.45、2.73。调控方案1的多目标总协同度为0.64,与初始方案保持一致,延迟时间与嵌入维数与初始方案相同,关联维数及K熵分别为3.76、2.08,分别较初始方案减少了0.69、0.65,说明该次对满意边界破坏点的调控起到了积极的作用,降低了水库群多目标调度系统的复杂程度和混沌程度。调控方案2的多目标总协同度为0.63,较调控方案1减小了0.01,关联维数及K熵分别为4.13、3.78,较调控方案1分别增加了0.37、1.70,其中K熵的增加尤为显著。
5.2 最终方案分析
以调控方案1作为黄河上游梯级水库群多目标均衡调控的最终方案,分析各子系统及序参量的有序度及利益值,结果分别见表5、6。
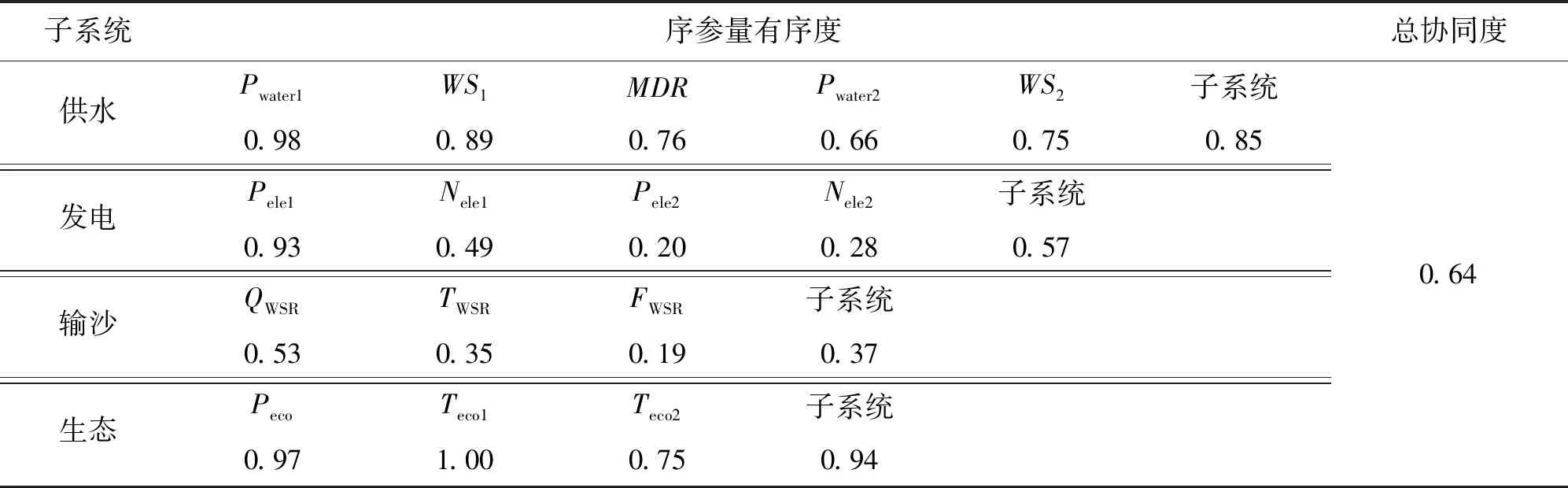
表5 最终方案多目标各子系统及序参量有序度多年平均值
由表5可知:(1)供水子系统序参量中,关键利益Pwater1、WS1、MDR的有序度分别为0.98、0.89、0.76,供水目标序参量中有序度最低的为非关键利益Pwater2(0.66),供水子系统有序度为0.85;(2)发电子系统序参量中,关键利益Pele1、Nele1的有序度较非关键利益Pele2、Nele2分别高出0.73、0.21,可见防凌期梯级水库群的发电保障程度不甚理想,发电子系统有序度为0.57;(3)输沙子系统序参量中,关键利益QWSR、TWSR的有序度分别为0.53、0.35,明显高于非关键利益FWSR的有序度,最终输沙子系统有序度为0.37;(4)生态子系统序参量中,关键利益Peco、Teco1的有序度分别为0.97、1.00,关键利益保障良好,生态子系统有序度为0.94。总体而言,供水、发电、输沙、生态各子系统的关键利益有序度均高于非关键利益,体现了梯级水库群多目标协同均衡调控以关键利益为保障重点的调控思路。
由表6可知:(1)供水目标中,河道外非农业用水的保证率Pwater1达到了98.46%,保障程度优良;农业关键期的总缺水量WS1多年平均值为2.77×108m3,较农业非关键期的总缺水量WS2减少了5.33×108m3;农业关键期最大缺水深度MDR为0.24,农业非关键期利益保障程度欠佳,供水保证率Pwater2为66.08%。(2)发电目标中,非防凌期的发电保证率Pele1及平均出力Nele1分别为93.07%、570.50×104kW,较防凌期相应值分别高出73.07%、245.00×104kW,防凌期的发电利益受防凌和多目标竞争影响,保障程度较低;(3)输沙目标中,调沙控制流量QWSR平均为2 639.55 m3/s,1次调水调沙历时TWSR平均为17 d,均达到调水调沙所需要求;长系列调沙频率FWSR为19.23%,即1990—2015年间进行了5次调水调沙,平均每5.2 a进行1次。(4)生态目标中,生态基流保证率Peco为96.92%,石嘴山及头道拐断面的1次生态脉冲Teco1均能得到保障,多次生态脉冲Teco2的平均值为3.75次,生态利益保障程度良好。
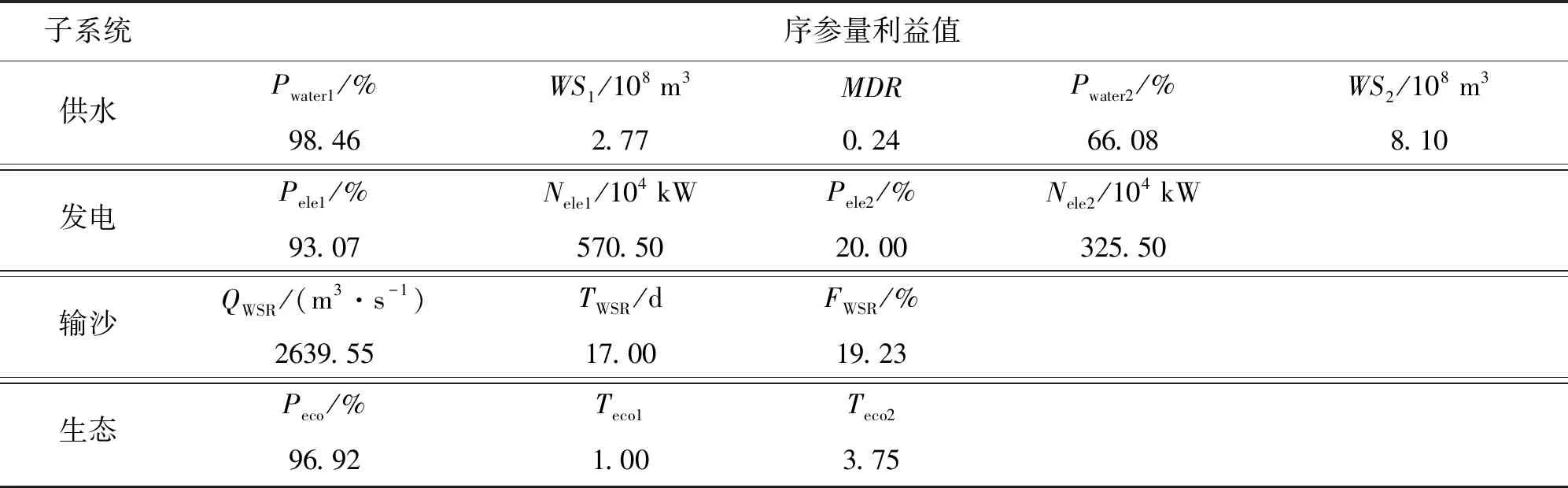
表6 最终方案各子系统序参量多年平均利益值
梯级水库群调度下多目标关键利益与非关键利益的长系列变化过程也是客观反映梯级水库群多目标保障能力的重要依据。图5显示了1990—2015年黄河上游梯级水库群供水、发电、生态目标的关键利益与非关键利益变化过程;表7为同期长系列过程中输沙目标的关键利益与非关键利益。
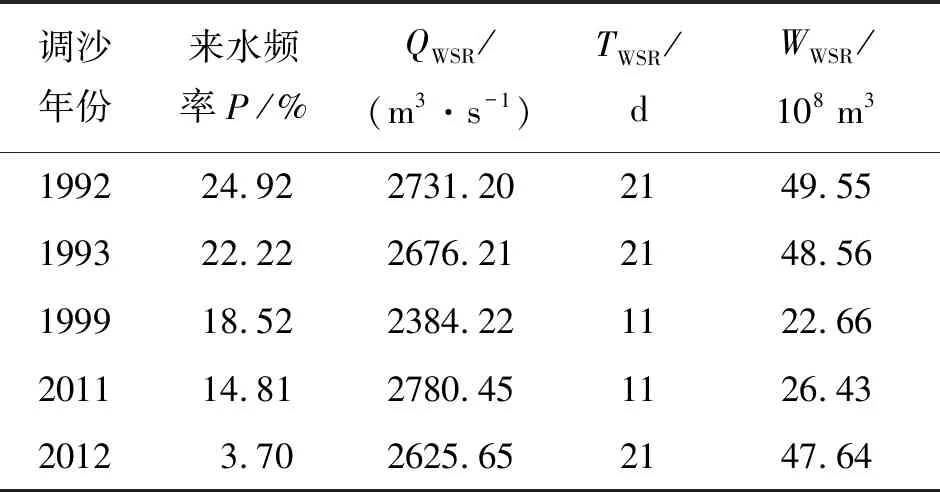
表7 1990—2015年黄河上游梯级水库群各调沙年份关键利益与非关键利益取值
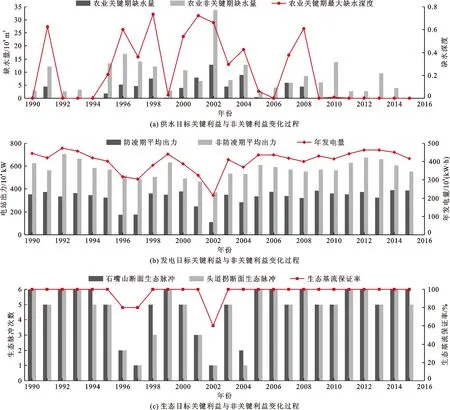
图5 1990—2015年黄河上游梯级水库群调度下多目标关键利益与非关键利益长系列变化过程
由图5(a)可以看出:(1)在梯级水库群1990—2015年长系列调度过程中,有11个年份的农业关键期不缺水,占总年数的42.31%;农业关键期缺水量较大的年份主要发生在2001—2004年,期间有2个连续枯水年,特别是2002年为特枯水年,龙羊峡年入库水量仅为99.28×108m3,该年农业关键期缺水量达到12.71×108m3。(2)长系列过程中有2个年份(1994、2015年)的农业非关键期不缺水,有9个年份的农业非关键期缺水量超过10×108m3,农业非关键期缺水量的最大值为2002年的33.82×108m3。(3)在农业关键期最大缺水深度的变化过程中,缺水深度的最大值为1998年的0.73,长系列调度过程中有7个年份的最大缺水深度高于0.5,占总年数的26.92%。
由图5(b)可以看出:(1)黄河上游梯级水库群非防凌期的平均出力变化过程中,最大值为1992年的711.58×104kW,最小值为2002年的369.11×104kW;整个调度期的前半段(1990—2002年)中有4个年份的非防凌期平均出力低于500×104kW,而后半段(2003—2015年)的非防凌期平均出力均高于500×104kW,说明2002年以后的非防凌期发电利益保障程度优于2002年之前,这主要是因为后半调度期的径流来水情况总体较前半调度期略丰。(2)受防凌约束及多目标矛盾竞争的影响,长系列过程中有5个年份的水库群防凌期平均出力低于300×104kW,最小值为2002年的111.20×104kW,其余年份在300×104~400×104kW之间波动。(3)梯级水库群年发电量过程中,最大值为1992年的473.37×108kW·h,最小值为2002年的214.93×108kW·h,2003年之前年发电量过程波动较大,2004年后受来水增多影响,水库群年发电量保持在相对较高的水平。
图5(c)显示,生态基流保证率变化过程中,除1996和1997年为80%、2002年为60%外,其余年份均为100%;以1旬为1次生态脉冲的持续时长,调度期内石嘴山断面有2个年份的生态脉冲仅为1次,有12个年份的生态脉冲次数为6次;头道拐断面有3个年份的生态脉冲次数为1次,有10个年份的生态脉冲次数为6次;调度期后半段(2003—2015年)石嘴山与头道拐断面的生态脉冲次数总体上多于前半段。总体而言,除个别年份生态目标满足程度较差外,大多数年份的生态利益均能得到保障。
由表7可知,在1990—2015年的26 a中,梯级水库群实施调水调沙的年份来水频率均小于25%,为丰水年或偏丰水年;5次调水调沙中,调沙流量最大值为2011年的2 780.45 m3/s,最小值为1999年的2 384.22 m3/s;有3次调沙历时为21 d,2次为11 d;单次调沙用水量的平均值为38.97×108m3。
6 讨 论
黄河这一典型的缺水型多沙河流的梯级水库群多目标优化调度问题,长期以来一直受到众多学者的关注和研究,也形成了丰富的理论、方法及成果。本文的研究成果及观点与多位学者的研究成果有一致及差异之处。
(1)梯级水库联合运行方式:本文黄河上游梯级水库群多目标协同均衡调控过程中,丰水年龙羊峡水库充分发挥多年调节水库的优势,在保障多目标关键利益及非关键利益的前提下尽可能多地蓄水,保持高水位运行,刘家峡水库进行年内径流调节;枯水年龙羊峡水库动用自身库容补水以“一水多用”的形式优先保障发电、供水、生态目标的关键利益,尽可能减少对非关键利益的破坏程度。多目标协同均衡调控过程中梯级水库群的运行方式与彭少明等[22]的研究成果一致。
(2)多目标用水矛盾解决方案:在刘百灵等[23]的研究中,枯水年(选取1990年7月至1991年6月典型年)以月为步长的黄河上游梯级水库群多目标优化调度结果显示,汛期梯级水库群为尽可能抬高发电水头而减少下泄流量,与该时期满足下游供水需求产生矛盾,导致7—9月梯级水库群发电量较小且灌溉缺水严重。本研究将5—9月细化为以旬为调度步长,并尽可能优先保障多目标关键利益,使得1990年7月至1991年6月的农业关键期缺水量为0,汛期梯级水库发电利益也得到较好保障。
(3)梯级水库群多目标利益值:在Bai等[24]的黄河上游梯级水库群多目标优化调度研究中,梯级水库调沙流量控制在2 580 m3/s,1次调水调沙历时为30 d,调度期1956—2010年中调沙频率为每4.8 a进行1次。在本研究中调水调沙流量及历时不设为固定值,而是在限定范围内由水库群多目标协同均衡调控模型进行优化,调沙流量的平均值为2 630 m3/s,调沙频率为每5.2 a进行1次,调沙历时平均值为17 d。本研究成果中的调沙流量虽较Bai等[24]的研究有所提高,但调沙频率降低、调沙历时缩短。主要原因一是所用径流序列不同,本研究所用径流序列(1990—2015年)的来水量总体偏少,1990—2015年黄河上游干流总径流量多年平均值为259.58×108m3,较1956—2000年序列多年平均值304.87×108m3(数据来源于黄河水资源公报)减少了45.29×108m3;二是其余目标的保障程度不同,Bai等[24]的研究中供水目标仅满足75%保证率要求,生态目标仅满足兰州断面300 m3/s的基本生态流量,不考虑生态脉冲,而本研究中供水利益保障程度更高,河道外非农业用水的保证率达到98.46%,农业用水保证率也高于75%,生态目标中需满足的石嘴山断面适宜及最小生态流量均高于300 m3/s,且满足生态脉冲需求。
由上述与其他学者的研究成果对比可知,本研究所提理论与方法能够获得有效的梯级水库群多目标优化调度方案,能够优先保障多目标的关键利益,降低水库群调度系统的混沌程度,适用于水资源有限条件下的梯级水库群多目标水资源利用研究。受作者专业水平、数据获取等因素的限制,本文还存在一定的不足,需在今后的工作中进一步深入研究。如本文对于黄河上游输沙目标的效果仅从调沙流量、调沙历时、调沙频率进行分析,未能量化调沙水量所对应的河道冲刷沙量;未来考虑进一步深入研究反映河道形态的输沙水动力学模型,结合梯级水库群多目标协同均衡调控模型量化输沙效果。
7 结 论
本文在运用并求解梯级水库群多目标协同优化调度模型的基础上,进一步提出了时段内多目标均衡调控方法及水库群调度系统的混沌特征识别与引导方法,并应用于黄河上游梯级水库群多目标优化调度。结论如下:
(1)梯级水库群多目标协同均衡调控理论与方法在黄河上游梯级水库群多目标调度的应用结果表明:通过水库群多目标协同优化调度与均衡调控,可实现梯级水库群调度下多目标在时段间的协同有序、时段内的利益均衡,并引导水库群调度系统降低了系统的复杂程度和混沌程度。
(2)黄河上游梯级水库群多目标协同均衡调控最终方案的多目标总协同度为0.64,其中生态子系统的有序度最高(0.94),其次是供水子系统(0.85),由于防凌期发电保证率及梯级水库平均出力受防凌流量限制影响,发电子系统保障程度较低(非关键利益有序度均低于0.3),导致发电子系统有序度仅为0.57,输沙子系统有序度为0.37,在多目标中利益保障程度最低,这是由于调水调沙是一项短时间内大量用水且需要长期择机进行的防淤减沙措施,1次调水调沙对后续较长时段的供水、发电、生态利益保障均有影响,因此在水资源量有限的情况下,长系列调水调沙的历时及频率保障程度均较低。
(3)黄河上游梯级水库群多目标协同均衡调控各目标的关键利益保障程度普遍高于非关键利益。其中供水目标的关键利益“河道外非农业用水保证率”多年平均值高达98.46%;发电目标的关键利益“非防凌期发电保证率”多年平均值为93.07%,较防凌期利益高出73.07%;输沙目标的关键利益均能满足1次调水调沙所需的流量及历时需求;生态目标的关键利益“生态基流保证率”多年平均值达到96.92%,生态脉冲也能得到有效保障。体现了梯级水库群多目标协同均衡调控以关键利益为保障重点的调控策略。
