桨-轴-艇耦合模型轴承分布式弹簧建模方法
2023-11-13贾泽坤张冠军
贾泽坤 陈 谦 张冠军
(武汉理工大学船海与能源动力工程学院 武汉 430063)
0 引 言
研究桨-轴-艇耦合系统声振特性,多数利用有限元法建立模型进行计算.而建模的合理性问题是分析桨-轴-艇耦合系统振动响应的前提,其中轴承刚度的合理建模影响螺旋桨激励力的传递特性,进而影响桨-轴-艇耦合模型的振动响应结果.
桨-轴-艇耦合系统建模时,轴承采用线弹性材料模拟,基于有限元法计算无阻尼下的振动响应,将轴承简化为弹簧单元以提高计算效率.各国船级社针对简化模型中的弹簧单元刚度和分布形式以经验值确定.周春良等[1]分析了轴承支承长度及间距对轴系振动的影响,分析得到船舶前后艉架轴承和艉管轴承对轴系的振动影响最大.徐颖蕾等[2]将推进轴系的艉轴承简化为一个弹性支承,得到了等效刚度模型.李晨阳[3]针对尾轴承、中间轴承和推力轴承其中的一种进行简化研究.劳坤胜等[4]针对水润滑橡胶艉轴承进行了谐响应分析.杨志荣等[5]基于有限元法分析对中间轴承进行了载荷识别.张晓东等[6-7]研究了不同弹簧刚度及弹簧单元的分布形式对轴系振动特性的影响.对于轴承简化为弹簧单元刚度的确定,而根据试验经验确定使得选取范围过大以及弹簧单元分布形式不同,导致仿真计算不准确.因此需要以桨-轴-艇耦合系统尾部模型为研究对象,综合考虑各个轴承的简化,分析弹簧单元的刚度及分布形式对振动响应的影响.
文中通过建立桨-轴-艇耦合系统尾部模型即原模型,根据推导的刚度简化公式将轴承简化为弹簧单元,基于有限元计算弹簧单元在不同刚度及分布下对振动响应的影响,并找寻最接近原模型振动响应结果的方案.
1 桨-轴-艇耦合模型有限元建模
1.1 桨-轴-艇耦合模型的建立
基于ANSYS经典界面建立桨-轴-艇耦合模型,以艉轴承外侧圆心为原点,以笛卡尔坐标系的X轴为模型轴向,Y轴和Z轴为模型径向,模型部分参数见表1.

表1 模型主要参数 单位:m
建立几何模型见图1.

图1 桨-轴-艇耦合系统几何模型
根据相关文献[8-10]赋予材料属性,螺旋桨、轴系、壳体和基座的材料密度ρ=7 800 kg/m2,弹性模量E=2.1×1011Pa,泊松比μ=0.3,其中的艉轴承、中间轴承及推力轴承可视作具有一定刚度的线弹性材料,轴承材料参数见表2,其中艉轴承的材料参数借鉴文献[4]的水润滑橡胶轴承的材料参数,中间轴承的材料参数借鉴文献[5]中建立中间轴承的材料参数.

表2 轴承材料参数
螺旋桨、轴系、轴承及轴承基座选用单元solid185模拟,壳体以及推力轴承基座选用面单元shell181模拟[11-12].轴承与轴系的接触部分为两个重复的面,并且两个面上的节点完全重合,建立重合节点的耦合约束,即在艉轴承和中间轴承以及推力轴承的前后支撑处为横向的节点耦合,推力盘处为纵向的节点耦合.有限元模型见图2.

图2 桨-轴-艇有限元模型
1.2 模型网格无关性验证
在计算桨-轴-艇耦合系统尾部模型的振动响应之前,通过相应的拓扑关系进行检验以保证模型的正确性.谐响应计算频率为200 Hz,收敛性验证需要将不同网格尺寸下的模型模态计算到400 Hz.不同网格尺寸下固有频率随单元尺寸变化关系曲线见图3.

图3 固有频率随单元尺寸变化
在443阶次下不同网格尺寸相同阶数下的固有频率见表3.

表3 不同网格尺寸下的模态频率
由表3可知:不同网格尺寸对固有频率值的影响较小,相同阶次下固有频率值随单元尺寸的减小而减小,随着计算阶次增大,固有频率值具有逐渐收敛的趋势.通过以上分析,为了节约求解资源、保证计算结果的准确性,选取的网格尺寸为80 mm,划分单元数为174 636.
2 桨-轴-艇耦合模型简化理论推导
根据相关理论及公式,推导每个轴承的刚度作为弹簧单元的刚度,计算刚度推导模型见图4.

图4 材料刚度推导示意图
设轴承材料变形为δ,轴承受力为F,应变为
ε=δ/h
(1)
式中:δ为轴承材料变形量;ε为应变;h为轴承厚度.
应力σ为
σ=Eε=Eδ/h
(2)
式中:E为材料的弹性模量.
轴承材料受力F为
F=Aσ=AEδ/h
(3)
式中:A为轴承接触部分的投影面积.
推导轴承材料刚度K,即简化后弹簧的刚度k为
(4)
式中:k为弹簧刚度;λ为刚度比例系数.刚度比例系数λ的引入是为了分析简化后弹簧刚度的变化对振动响应结果的影响.
3 桨-轴-艇耦合模型轴承分布弹簧建模
3.1 建立单排弹簧简化模型
在艉轴承后端1/4处从水平和垂向的两个方向上建立弹簧单元等效艉轴承对轴系的径向支撑;在中间轴承1/2处从水平和垂向的两个方向上建立弹簧单元等效中间轴承对轴系的径向支撑;在推力盘前后支撑轴承距离为0.2 m的位置建立垂向和水平两个方向上的弹簧单元来等效推力轴承前后端的径向支撑;在推力盘的中段处沿圆周方向间隔90度设置4个弹簧单元来等效推力轴承的纵向支撑.根据式(4)的换算刚度公式,设置弹簧刚度参数k见表4.

表4 弹簧刚度参数 单位:N/m
建立弹簧单元分布见图5.
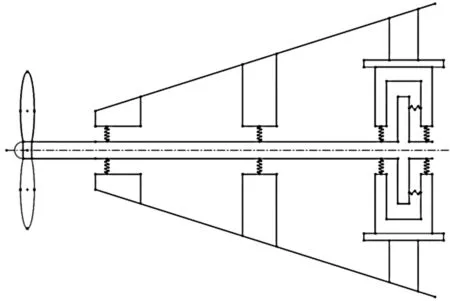
图5 单排弹簧模型示意图
3.2 建立多排弹簧简化模型
在艉轴承后端0、1/2及1处从水平和垂向的两个方向上建立弹簧单元艉轴承对轴系的径向支撑;在中间轴承0、1/2及1处在从水平和垂向的两个向上建立弹簧单元等效中间轴承对轴系的径向支撑;在推力盘前后支撑轴承距离为0.2 m的位置建立垂向和水平两个方向上的弹簧单元来等效推力轴承前后端的径向支撑;在推力盘的中段处沿圆周方向间隔90°设置4个弹簧单元来等效推力轴承的纵向支撑.设置弹簧参数见表5.

表5 弹簧刚度参数 单位:N/m
建立弹簧单元分布见图6.

图6 多排分布弹簧模型示意图
4 不同建模方案桨-轴-艇耦合系统计算结果对比
4.1 桨-轴-艇耦合模型模态分析
计算原模型、单排弹簧模型及多排分布弹簧模型在空气中的模态,截取前30阶固有频率绘制曲线见图7.

图7 各个模型模态频率结果对比
对比原模型、单排弹簧模型及多排分布弹簧模型的固有频率可知:单排弹簧模型和多排分布弹簧模型在前16阶的固有频率基本一致,并且单排弹簧模型和多排分布弹簧模型与原模型整体上固有频率相近;在16阶到21阶时随着刚度比例系数λ的增大,对应频率则更接近于原模型频率,而在相同刚度比例系数下多排弹簧对应频率更接近于原模型;在21阶到30阶,刚度比例系数的大小和弹簧等效的类型对频率影响不大;在25阶之后,两种弹簧简化模型的固有频率接近于原模型.
限于文章篇幅,选择一组整体形变最大的振型图进行分析,其中选取刚度比例系数λ=1时的单排弹簧模型和多排分布式弹簧模型与原模型的振型对比结果见图8.

图8 各个模型的振型图对比
由图8可知:三种模型在对应频率时的振型变化一致,轴承简化为弹簧单元对模型结构特性没有太大的影响.
4.2 浆-轴-艇尾部耦合模型振动响应分析
计算桨-轴-艇尾部耦合原模型与单排弹簧模型和多排分布弹簧模型的谐响应,在壳体大端施加简支约束,在螺旋桨导流帽端施加纵向和横向为1 N的激励力,激励力施加位置见图9.

图9 激励力施加位置示意图
计算各个模型的振动响应,计算频率范围为10~200 Hz,步长为2 Hz.
在施加纵向和横向激励条件下,计算弹簧单元不同分布下的振动响应,提取外壳节点的均方速度级曲线见图10.

图10 各个模型均方速度级曲线
由图10可知:轴承简化为弹簧单元对纵向力下的振动响应结果影响较大,在50 Hz以内结果相近,而在高频时结果不对应,这是由于纵向力主要通过推力轴承传递激励,而原模型中推力轴承与轴系为面接触,简化为弹簧单元后,接触形式变为点接触,对振动响应结果有影响.在横向激励力下,在低频100 Hz以内的峰值处时,多排分布弹簧模型的振型响应曲线更接近原模型.因此,后文主要对比多排分布弹簧模型刚度变化对声振特性的影响.
计算多排分布弹簧模型在不同刚度比例系数λ下的振动响应,对比纵向和横向力条件下不同刚度比例系数的振动响应结果,提取图11测点处的振动速度级,整理并分析.
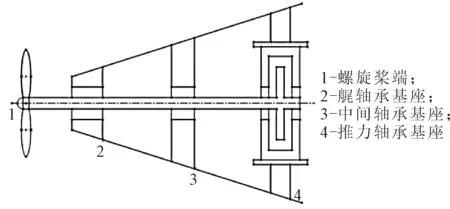
图11 振动响应提取测点位置示意图
在施加纵向力条件下,提取不同测点的振动响应曲线见图12.
多排分布弹簧模型的设置上主要考虑的是横向弹簧的分布等效,而从上图结果来看弹簧刚度不同,对纵向力下的振动响应结果影响不大.原模型是在纵向的节点耦合接触,在200 Hz以内分析频段出现峰值的次数少,对应出现峰值的频率与多排分布弹簧模型频率相差最大为10 Hz.
计算在施加横向力条件下的振动响应,提取各模型测点处振动速度级曲线见图13.
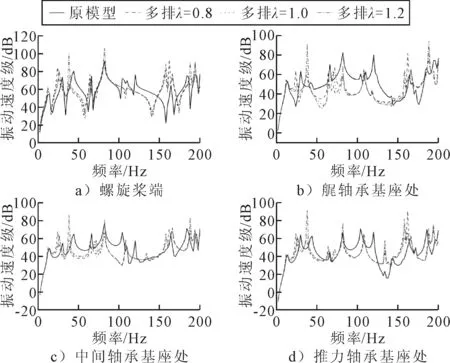
图13 横向力下测点振动速度级曲线
由图13可知:在施加横向力条件下,从上述四个测点的振动曲线看,在刚度比例系数λ=1时的多排分布弹簧模型的振动特性曲线峰值对应频率和振动速度级幅值与原模型结果接近.提取壳体表面所有节点的均方振动速度级,绘制曲线见图14.
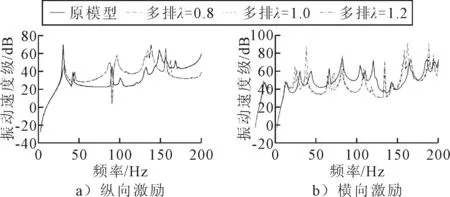
图14 各个模型均方速度级
由图14可知:在纵向激励力下,弹簧刚度变化对多排分布弹簧振动响应的结果影响不大;在横向激励力下,在刚度比例系数λ=1时,多排分布弹簧模型与原模型的振动响应曲线峰值对应频率和振动速度级幅值与原模型结果相近,在低频50 Hz之内的两个峰值处,振动响应的速度级幅值相差不到1 dB.
5 结 论
1) 弹簧单元的分布形式对纵向力下振动响应有影响,并且原模型对比结果不一致.在横向力下,多排弹簧简化模型的振动响应结果更接近原模型.因此在分析横向力条件下的振动响应结果时,可将各个轴承简化为弹簧单元来模拟,结果具有一致性.
2) 弹簧刚度的变化对纵向力结果没有太大影响,而在横向力下,在刚度比例系数λ=1时,多排弹簧简化模型的结果更接近原模型.在实际工程应用中,可将尾轴承、中间轴承简化为多排分布式弹簧单元,依照刚度简化式(4)设置弹簧单元刚度,得到的振动响应结果与原模型更为接近,在复杂模型的计算中,可充分减少计算时间,提高计算仿真效率.
