基于低空救援的无人机起降点选址问题研究
2023-11-13李松锐孙丽超
高 翔 张 明 李松锐 刘 旭 孙丽超
(南京航空航天大学民航学院 南京 211106)
0 引 言
无人机具有体积小、灵活轻便的优点,但无人机航程有限难以执行大规模的探测搜救任务.而直升机具有航程大、受天气影响小,以及机动性强等特点,相比于车辆具有移动速度快、受地面状态影响小的优点,因此在地震发生后利用直升机和无人机协同搜救可以充分发挥两者的优势[1].Carlsson[2]论证了车辆和无人机的使用效率,证明了使用车辆和无人机协同搜救的潜在效益与车辆和无人机之间的速度比的平方根成正比.Wang等[3]针对多辆卡车和无人机引入了无人机车辆路径问题,论证了协同作业下效率的提高.San等[4]在无人机和无人车协作的模型中考虑了实际飞行中的约束条件,来求解路径问题.Chowdhury等[5]针对无人机携带设备的重量和能耗之间的关系建模,估算无人机能实际覆盖的飞行范围来求解无人机的航迹规划问题.Dorling 等[6]通过建立一个有效载荷不同的无人机能量消耗模型解决了多无人机路径规划问题.
针对载体和多无人机协作的无人机起降点选址问题.Sergio等[7]提出了一辆卡车和多架无人机的新模式,设置无人机的起飞降落点为同一位置,利用k-means聚类算法来确定位置无人机的起降点.Freitas等[8]为了确定无人机的起降点提出了一种混合启发式算法,初始解由TSP求解器生成,之后使用混合启发式算法求解得出无人机的起降点和卡车的路线.Agatz等[9]假定无人机每次起飞和降落必须在相同位置,利用局部搜索的方法来确定无人机的起降点.Bouman等[10]为了确定载体和多无人机的协作下无人机起降点问题,提出了一种动态规划的精准方法,该方法以能够求解出更大规模的实例.杨雷博等[11]提出了一种在限制区下一辆车携带多架无人机的货车支持无人机配送解决方案,并构造了以最小服务时间为优化目标的双层规划求解方法.曹峰等[12]提出了一种面向大面积巡检区域的巡检车路径规划方法,巡检车在每个驻车点处驻车一次,多架无人机由巡检车起降平台上起飞,前往各自目标杆塔完成相应的巡检任务,且要求无人机必须同点起降.刘艳秋等[13]提出货车和无人机“协同+并行”混合配送模式,以总运营成本最小为目标,建立了搭载多架无人机的车辆路径问题混合整数规划模型.彭勇等[14]构建了卡车无人机协同配送的路径优化模型,考虑一辆卡车与多架无人机进行配送,且配送客户需要让卡车在服务的客户点等待无人机完成配送任务并回收后才继续下一个点的配送服务.曹英英等[15]基于集群提出卡车与无人机联合配送新模式,考虑一辆卡车配有多架无人机进行配送,并提出两阶段算法,通过改进后的K-means算法求出卡车停靠点,采用遗传模拟退火算法优化卡车与无人机联合配送路线.
针对无人机起降点选址的建模中,大多将无人机的起飞点和降落点设置为同一位置,没有考虑无人机实际飞行中在执行完搜救任务后可能会就近降落,导致选址成本较高.而且模型的约束中很少考虑环境温度、无人机的负载以及飞行姿态对无人机的续航能力的影响.文中针对传统的无人机本地起降模式选址模型进行改进,将无人机运行时的环境温度、无人机的负载,以及无人机的飞行姿态对无人机续航能力的影响作为模型的约束,在模型中不要求无人机的起降点为同一位置,使得对无人机起降点的选址问题更加符合实际,降低选址成本.
1 无人机飞行状态对续航能力的影响
文中基于气动理论建立旋翼无人机的理想化的近似功耗模型[16].
1) 无人机悬停时的功率方程为
(1)
2) 无人机水平飞行时的功率方程为
(2)
式中:ρ为空气密度;W(N)为总重量;ζ(m2)为旋翼面积;Vhor为无人机水平飞行的速度;α(Vhor)为水平飞行时的迎角;ηhor为水平飞行时的效率系数;α(Vhor)、ηhor均为经验系数,文献[16]中利用实测数据根据最小二乘法计算得出.
(3)
(4)
S′=vtσ1
(5)
(6)
式中:σ1为无人机携带负载悬停的时的功率与无人机空载水平飞行时功率的比值;σ2为无人机携带负载水平飞行时的功率与无人机空载水平飞行时功率的比值.设无人机水平飞行时间为t,悬停时间为t′,无人机的水平飞行速度为v.
负载条件下无人机水平飞行时间t,对应标准情况下(无人机空载、运行环境温度为25℃)无人机航程S′'由所示.负载条件下无人机悬停时间为t′,对应标准情况下(无人机空载、运行环境温度为25℃)无人机航程为S″由所示.
2 运行环境温度对无人机续航能力影响
利用无人机低空搜救时仅考虑环境温度对无人机续航能力的影响,引用锂离子电池在不同运行温度下实际的电池容量见表1,锂离子电池标准容量为环境温度为25℃下的的电池容量.利用不同的拟合方法求得锂电池容量变化与温度的关系,建立锂离子电池实际容量与环境温度的函数关系.

表1 电池的容量随外界温度变化表
根据SPSS的实际运行结果,汇总了实测结果中环境温度与电池容量拟合的三种线型的参数表见表2,图1为拟合曲线图.

图1 温度-电池实际容量拟合(实测散点图与三类拟合曲线)

表2 温度-电池实际容量拟合参数表

δx=0.98+6.72×10-4x+3.11×10-5x2-
8.27×10-7x3-20≤x≤25
(7)
(8)
式中:x为无人机搜救过程中的环境温度,℃;δx为在环境温度为x时,电池的实际容量与理论容量的比值,其物理意义为在当前温度下锂离子电池容量与标准电池容量的比值;v为无人机的水平飞行速度;t″为最大飞行时间.
3 无人机异地起降选址模型
直升机和无人机协同搜救无人机的本地起降模式见图2a),直升机放飞无人机后在原地等待无人机搜救任务完成后进行回收,回收后执行下一组任务.协同搜救的异地起降模式见图2b),直升机放飞无人机后直接飞往下一点来回收无人机,交替进行完成任务.

图2 本地起降模式与异地起降模式
模型假设:①待搜救点已经确定,每个待搜救点只需且只能被探测一次;②考虑无人机实际避障带来的影响,设置预留能耗系数;③每个待搜救点的探测时间已知,无人机携带负载下的悬停时间和飞行时间的转为为无人机标准情况下(无人机空载、运行环境温度为25 ℃)的航程;④忽略了无人机的在起飞和降落的具体状态每架无人机的起飞和着陆都可以瞬间完成;⑤无人机在直升机上能自动充电或更换电池.
考虑无人机的负载、无人机的飞行状态、运行环境温度变化对无人机续航能力的影响,针对以往研究中的选址模型进行改进,建立直升机和无人机协同搜救的无人机异地起降选址模型.
考虑以搜救费用最低为目标函数,目标函数为
(9)
(10)
Sb,k,l≤Sδx,b,l∈M',k∈M
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
xb={0,1},b∈M′
(19)
(20)
pl={0,1},l∈M′
(21)

式(10)为无人机考虑悬停、负载情况下的无人机实际航程;式(11)为在环境温度为x时需要满足的无人机续航能力要求;式(12)为每个待搜救点只由一个无人机起降点为其服务;式(13)为每个待搜救点只由一个无人机降落点为其服务;式(14)为一组无人机起降点可以服务多个待搜救点,每个待搜救点只能由一组无人机起降点为其服务;式(15)为选出的无人机起飞点数量和无人机降落点数量一定要相等;式(16)为当b被选成无人机起飞点时才可能存在待搜救点k由该点起飞的无人机服务;式(17)为若l点被选中为无人机的降落点才可能存在待搜救点k无人机服务完成降落;式(18)为无人机由b点出发飞向待搜救点k则为1否则为0;式(19)为b被选选作无人机起飞点则为1否则为0;式(20)为无人机从待搜救点k飞回降落点l则为1,否则为0;式(21)为l被选作无人机降落点则为1,否则为0.
4 算法设计
运用改进的二进制粒子群算法求解无人机起降点选址问题.每个粒子表示一种选址序列,1表示该组起降点被选中,0表示该组起降点未被选中.算法设计中的变量与含义见表3.

表3 算法设计变量表
初始化种群是将若干组备选无人机起降位置两两组合,用这种方式求解满足了模型中的的限制,从组合中选取无人机起降点,针对式令α和αk分别为.
(22)
αk=tkv
(23)
则式(2)~(10)可以化简为
Sb,k,l=(db,k+dk,l)ασ1+αkσ2
(24)
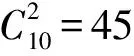
Z1为选址成本即式,无人机起降点选址成本越小越符合要求.
(25)
传统的粒子群算法在迭代计算的过程中线性减少权重w,但是运算中仅仅只减少w,容易使函数收敛到局部极值点.为解决此问题本文在求解无人机起降点选址问题时中采用惯性权重动态改变的方法:
(26)
(27)
(28)
(29)

基于改进二进制粒子群算法求解异地选址问题的步骤如下.
步骤1确定粒子群规模m,最大迭代次数n,以及参数c1,c2,r1,r2,w,生成距离矩阵.
步骤2将无人机起降点按照组合的方式产生,按照上文介绍的种群初始化的规则随机产生m个可行解X1,X2,X3,…,Xm,每个解的矩阵行数为待搜救点的组合数.找到未开放的选址组合在距离矩阵中相应位置为无穷大,找到每行中非0以外的最小位置,并生成指派矩阵满足(14)、(15),并判断矩阵中的解是否满足式(10)、(11).若满足按照式(25)计算Xi的适应度并且将初始适应度作为初始个体极值Pbest,i,由于异地选址问题中的目标函数是搜救费用满足最低要求,所以将所有Pbest,i中的最小值赋给Gbest作为初始全局极值,vi的初始值设为0.
步骤3在更新后按照式(25)计算更新后每个个体对应的无人机起降点选址成本,并且按照式(26)、(27)跟新惯性权重w,如果粒子i的无人机起降点选址成本低于此前个体极值Pbest,i,则将其置为Pbest,i,如果最佳的Pbest,i优于此前的全局的极值Gbest则将其置为Gbest.
步骤4如果满足收敛条件或达到的最大迭代次数,就停止计算,否则返回步骤3.
5 算例分析
5.1 数据获取及相关参数设计
以2010年4月14日玉树地震为例,选取在该地震带上受灾较为严重的玉树县和称多县.选择100个点作为待搜救点,生命探测仪DKL LifeGuard TM在开放空间搜救距离可达500 m以上,水面达1 km以上,在碰到障碍物时侦测范围会减少.无人机型号为科卫泰X6L,详细参数见表4.
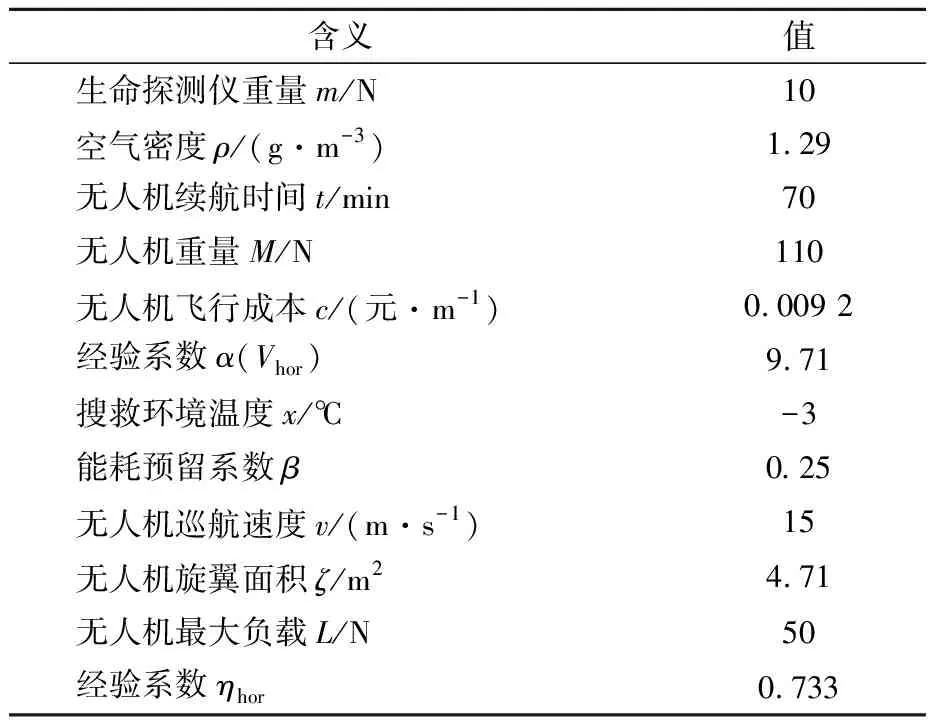
表4 相关参数表
5.2 无人机起降点的选址
利用改进的二进制粒子群算法求解无人机起降点的选址模型,算法的设置见表5.

表5 粒子群算法参数设置表
粒子群算法具有随机性,因此每次求解运算10次,以10次的平均值作为最终的解.以30个待搜救点数量为例,运用改进二进制粒子群算法迭代100次,求解模型相关参数,得到对应的无人机起降点组合以及对应的待搜救点和相应的选址成本,并且与未改进的粒子群算法进行对比的迭代结果见图3,分别求得无人机异地起降模式下的选址总成本为2 185.401元和无人机本地起降选址模式下的总成本为2 966.596元.
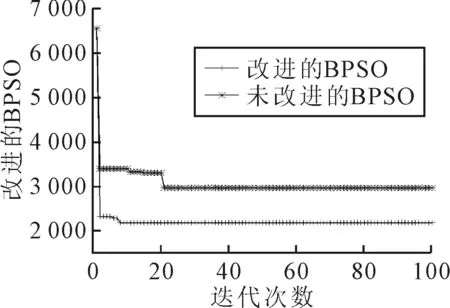
图3 改进的二进制算法和其他算法迭代效果对比
求解无人机起降点选址模型得到的解为若干组无人机起降点以及每组起降点对应的待搜救点.在选址阶段我们不要求得到无人机的数量与飞行计划,在后续的无人机任务分配的基础上规划出直升机的航线后,根据执行各个子任务的顺序,各组子任务的无人机的起飞点和无人机的降落点将会被确定.
30个待搜救点规模下的求解结果见表6.由表6可知:30个待搜救点数量下的求解结果共选出4组无人机起降点即将整个搜救任务分成4组子任务.

表6 30个待搜救点规模下无人机起降点选址结果
继续求解50个待搜救点规模下,80个待搜救点规模下,100个待搜救点规模下的选址问题,结果见表7~9.

表7 50个待搜救点规模下无人机起降点选址结果

表8 80个待搜救点规模下无人机起降点选址结果

表9 100个待搜救点规模下无人机起降点选址结果
5.3 文献对比分析
选取30、50、80和100个四种规模不同的待搜救点进行验证,求解本地起降与异地起降的选址成本和方案,见图4.

图4 不同数量待搜救点下的本地选址成本与异地选址成本对比
计算出10次运算后选址成本的均值,并且计算成本变化率,见表10.
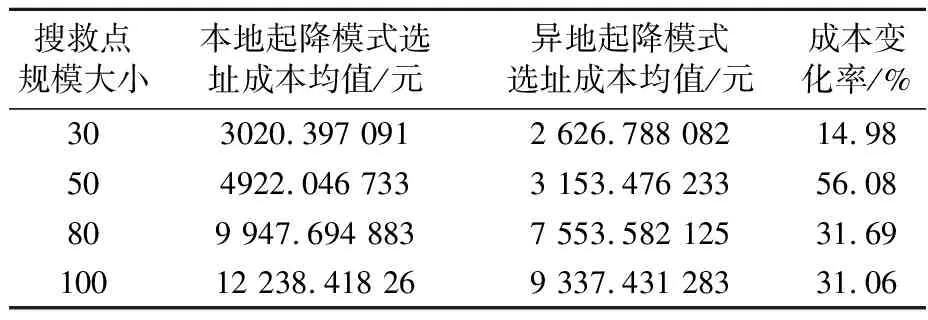
表10 两种模式不同规模下选址成本均值以及成本变化率
成本变化率=[(|本地起降模式选址成本均值-异地起降模式选址成本均|)/异地起降模式选址成本均值]×100%
6 结 束 语
本文提出了考虑无人机的运行环境温度、无人机负载、无人机的飞行状态作为模型约束,在此基础上建立直升机无人机协同搜救的无人机异地起降选址模型,利用二进制粒子群算法求解时引入了动态调整惯性权重的方法,通过算例证明了改进后的算法改进了其容易产生局部最优解的缺陷,从而得到较优得结果.在30、50、80、100个待搜救点规模下本文所建立的模型相对以往的研究选址成本分别降低了14.98%,56.08%,31.69%和31.06%.
在本文的设置的搜救环境下考虑温度对无人机续航能力的影响时,极端条件设置的温度系数为玉树地区四月月均温最低值,但实际搜救过程中环境温度在不断变化,因此在后续的研究中可以考虑无人机续航能力随温度的动态变化.
