针对过载控制的神经网络制导律研究
2023-11-13赵云凯王育欣
王 欣,赵云凯,王育欣
(1.沈阳理工大学 装备工程学院, 沈阳 110170;2.天津农学院 计算机与信息工程学院, 天津 300392)
0 引言
空中拦截问题研究初期,所设定的被拦截对象多为载人飞行器或弹道导弹。这种目标的特点为速度较低,机动性能有限,因此初期研究对象可看作小机动类型。比例导引法针对该类目标具有良好的拦截性能,且在战争中取得了亮眼的成绩[1-3]。然而,随着发动机技术及计算机控制技术的发展,拦截问题的研究更多地聚焦于机动性更强、飞行速度更快的飞行目标拦截案例。在这些案例中,目标多为高机动高突防能力的现代飞弹。这些目标的飞行轨迹多变,同时其弹载计算机具有足够的计算能力且能保证其在大机动规避动作后仍可以命中既定目标。故对被用于应对这种目标的新一代拦截飞弹提出了2个方面的要求:一是提高弹载设备的物理性能,二是改进现有制导律减小对大机动目标的脱靶量。
传统比例导引法在工程应用中的优点使其仍为目前主流使用的制导方法,但是,在针对大机动飞行目标的拦截中,虽然比例导引法仍具有理论上较优秀的拦截性能,但是随着目标机动,需用法向过载随着弹-目目标线旋转角速度急剧波动,从而导致脱靶量增加。因此,如何控制比例导引法在拦截大机动目标时的过载已成为一个重要的研究方向[4-6]。
本文中对比例导引律的需用过载与比例系数之间的关系进行数学推导和深入的分析,在命中目标的前提下,给出关于比例系数在满足导引律的需用过载小于可用过载的约束条件。根据过载与加速度的关系,在三维坐标系中,推导一种纯比例导引律加速度表达式,据此研究一种自适应控制比例系数的径向基函数神经网络(RBF)制导律,并给出详细的算法模型。经过仿真,验证在面对大机动高空飞行目标时,该导引律的过载表现优于传统比例导引律。
1 纯比例导引律拦截过程的过载
1.1 导弹拦截过程中的过载
导弹飞行过程中主要受发动机推力P、导弹控制机构改变导弹外形所产生空气动力R、空气阻力X及地心引力G的影响,根据牛顿第二定律,其合力效果与导弹之间具有如下关系[7]:
am=P+R+X+G
(1)
式(1)中:a为导弹质心的加速度;m为导弹的质量。
由于战术导弹在拦截目标的过程中,其拦截距离较近、飞行高度较低,因此在拦截过程中,地心引力G对其而言是唯一不受导弹运动状态影响的因素。因此将其作为度量的参考量,将发动机推力P、空气动力R、空气阻力X的合力设作N,建立式(2)进行过载定义,即:
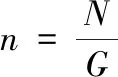
(2)
或用牛顿第二定律对式(2)进行改写,便获得了制导律研究中过载的常用表达形式。
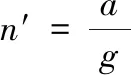
(3)
1.2 纯比例导引律(PPN)的需用过载分析
根据PPN制导律导引关系方程,可以给出PPN制导律过载的一般形式为
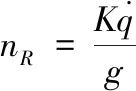
(4)
由弹目运动关系得:
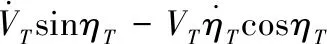
(5)
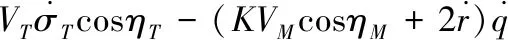
(6)
式(5)、式(6)中:r为导弹相对目标的距离;q为目标线与基准线的夹角,即目标线角;ηT为目标速度矢量前置角。
1.2.1导弹以恒定速度VM拦截以恒定速度VT作直线运动的目标
将所设定的条件代入弹目运动关系方程,可得
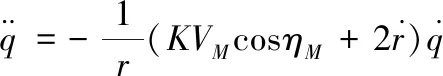
(7)

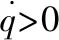

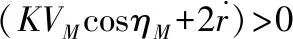
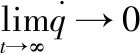
(8)
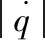
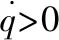

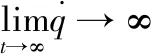
(9)
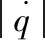

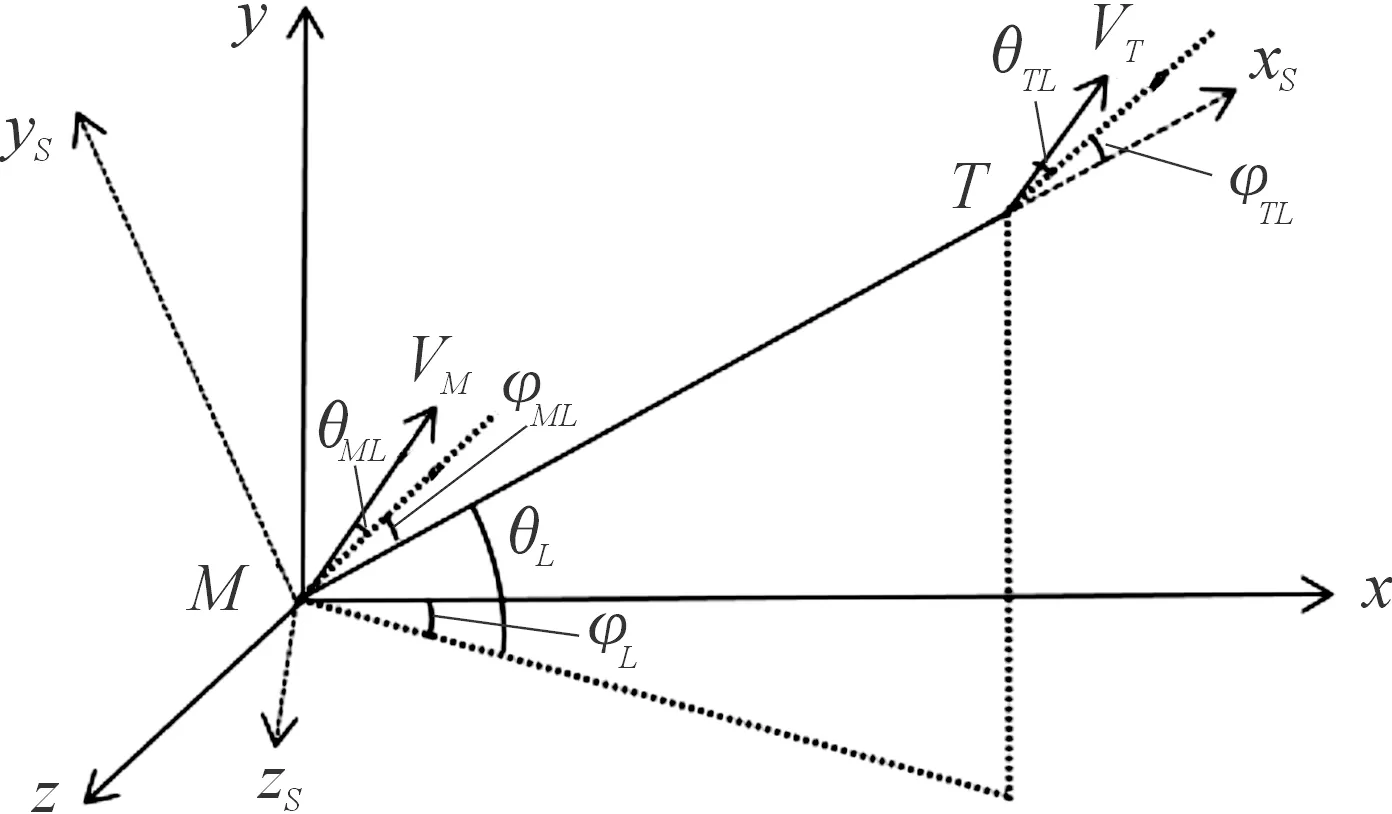
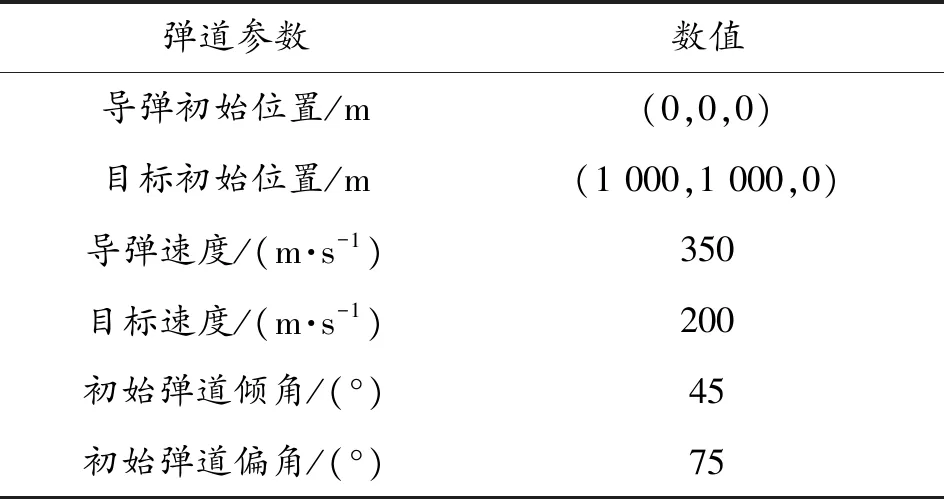
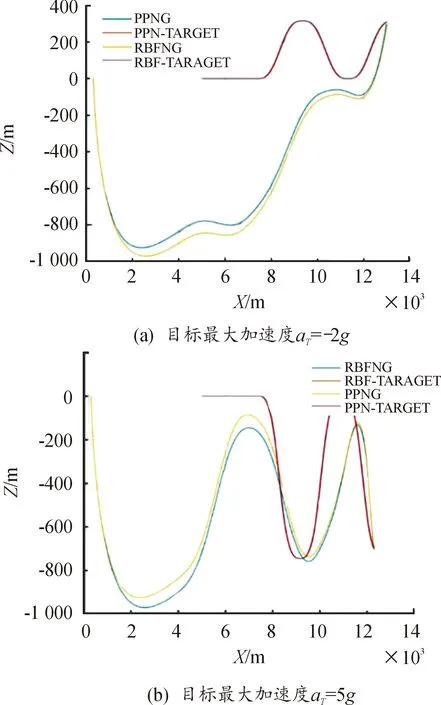
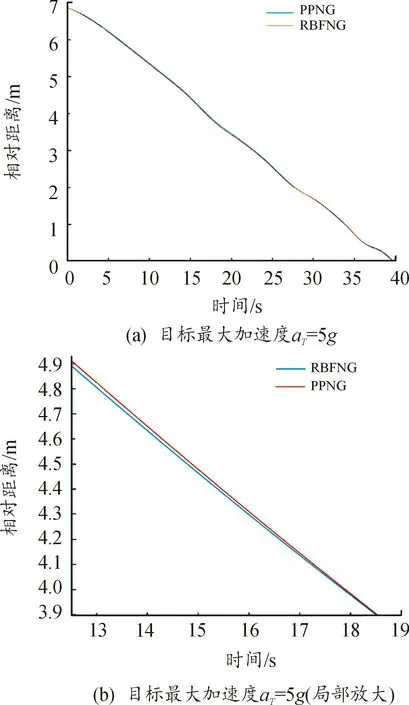
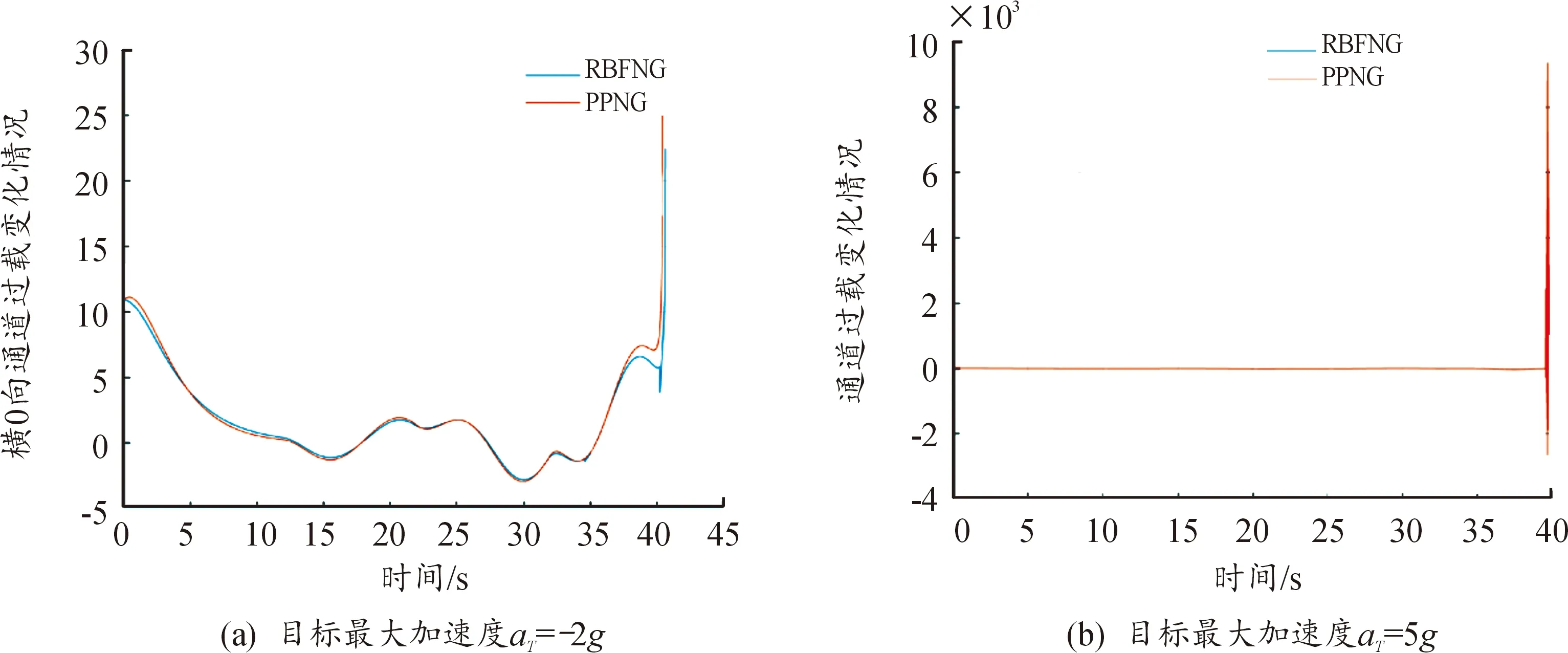
nR (10) (11) 1.2.2导弹以恒定速度VM拦截以恒定速度VT作机动运动的目标 (12) (13) (14) (15) 在PPN制导律的制导过程中,由于导弹法向加速度与弹-目目标线旋转速率始终成正比例关系,因此在视线坐标系基础上建立三维弹目追击模型,如图1所示。 图1 常用坐标系间转换关系图 图1中,Axyz为惯性坐标系;Oxsyszs为LOS坐标系;VM、VT分别为导弹、目标速度;θL为Oxs轴与Axz平面夹角;φL为Oxs轴于Axz平面投影与Ax轴夹角;θML、θTL分别为VM、VT与Oxszs平面夹角;φML、φTL分别为VM、VT于Oxszs平面投影与Oxs轴夹角。 某瞬时弹目相对速度为: (16) 某瞬时,弹-目目标线在纵向通道的旋转角速率为: (17) 某瞬时,弹-目目标线在偏航通道的旋转角速率为: (18) (19) 根据PPN制导律导引关系方程,得导弹指令加速度为 (20) (21) (22) (23) 由于工程实现中,控制系统的响应存在迟滞,且其响应幅度存在限制,因此为了保证控制系统的稳定工作,K的取值范围取[3,9]。 由导引关系方程得: (24) (25) 此时,导弹飞行的纵向通道与偏航通道由不同的比例系数KY、KZ分别控制,使控制效果更灵活,在保证过载控制的情况下,可以更精准快速地命中目标。 (26) 图2 RBF神经网络制导律结构 输出层权值更新规则为 (27) 聚类中心更新规则为 (28) 式(27)、式(28)中,η为BP网络学习速率,取值范围(0,1]。 表1 基于RBF神经网络制导律仿真初始条件 图3 amx=5时的弹目轨迹 图4 amx=-2时的弹目轨迹 由图3、图4可以看出,RBF神经网络与常值纯比例导引法均可以在以上2种机动条件下准确命中目标,且二者轨迹在空间中间距较近。因为图2所构造的压制函数将神经网络制导律的比例系数K的输出范围压制在[3,9]之间。因此在目标机动性能没有过高的时候二者轨迹相对相似,如图4所示,当目标最大机动能力仅有2g时,二者弹道轨迹相似度相比图3所示目标机动能力达到5g时要高。将这2种情况的弹道投影至水平面进行分析,如图5所示。 图5 Oxz平面轨迹 由图5可以明显看出,RBF神经网络制导律所追击的目标与常值纯比例导引律所追击目标二者运动轨迹是重合的。目标的机动条件为相对距离R<8 000,说明在目标机动之前,RBF神经网络制导律与纯比例导引律二者之间的相对接近速度是一样的,二者的制导参数此时尚未发生较大变动。当目标开始机动时,纯比例导引律的轨迹明显有了一个较大曲率。这是由于纯比例导引律选取的常值作为比例导引系数,当目标由匀速直线运动突然转变为正弦机动时,运动状态的突变导致了此时视线角速率在极短的时间内产生了变化,此时导弹的弹道偏角变化率也随之波动,因而造成了二者轨迹上的分离。RBF神经网络制导律则是通过不断调整K值,使得其飞行轨迹相较于纯比例导引律而言,曲率更小。 图6直观地对导弹轨迹的变化做出了解释,纯比例导引律的弹道偏角在目标开始机动时,出现了较大变化趋势,且变化方向与图5一致,这也验证了上述结论。同时,二者的弹道偏角的变化,说明了RBF神经网络对比例系数K值的自适应调整在起作用,过载表达式为 (29) 当目标运动状态突然改变时,适当降低比例系数对过载的控制是有益的。 图7给出了目标不同过载情况下,相对距离的变化。在接近目标前,任选一段时间的相对距离曲线可以发现,RBF神经网络制导律的相对距离曲线落于纯比例导引律相对距离曲线的下方,符合所构建的RBF神经网络模型的学习规则。在学习规则中,以瞬时的相对距离作为损失函数,使得K值的变化始终向弹目相对距离减小的方向进行。 图7 弹-目相对距离变化情况 图8给出了在不同机动目标下RBF神经网络制导律和纯比例导引律的偏航通道过载情况。在2种条件下,RBF神经网络制导律对过载幅值的优化要强于纯比例导引律。 图8 不同机动目标下RBF神经网络制导律和纯比例导引律的偏航通道过载情况 图9为弹-目相对距离与过载震荡点对比图。将图8(b)在命中点区域进行局部放大如图9(a)所示,RBF神经网络制导律在命中点附近,其过载较纯比例导引律相对平稳。从幅值上看,RBF神经网络制导律在目标进行较大机动时,其过载峰值远小于纯比例导引律;从震荡频率上看,RBF神经网络制导律的频率远小于纯比例导引律。同时,RBF神经网络的偏航过载出现震荡时间也滞后于纯比例导引律。将图8于对应位置放大,如图9(b)所示,此时RBF神经网络制导律的震荡位置滞后于纯比例导引律的震荡位置。从而RBF神经网络制导律对过载控制确实起到了很好的作用。 图9 弹-目相对距离与过载震荡点对比图 针对三维空间中变量繁多关系复杂的特点,建立三维落角约束下的弹目追击模型,并在此基础上进行带有落角约束的RBF神经网络导引律的研究,给出了各层详细的算法。通过对导弹飞行中的参数的合理选择,提出一种基于RBF神经网络的比例系数K值自适应制导律并进行了MATLAB数学仿真。仿真结果表明: 1) RBF神经网络导引律可实现对落角的约束,具有良好的拦截性能。 2) 该导引律在过载整体平稳的状态下,可以通过比例系数的自适应调整,抑制视线角速率抖振,并实现对导弹制导过程中的优化。 3) 在面对大机动高空飞行目标时,该导引律的过载表现优于传统比例导引律,该结果在工程实践中具有一定的参考价值。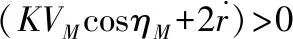
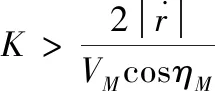
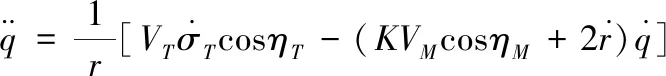
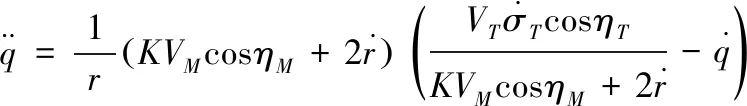


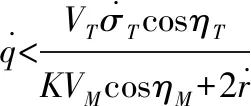
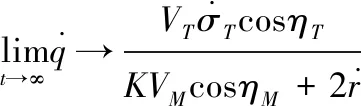
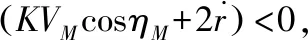

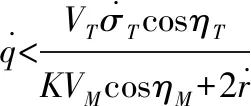
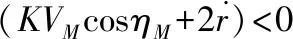
2 基于RBF神经网络的制导方法研究
2.1 三维PPN制导律加速度分析

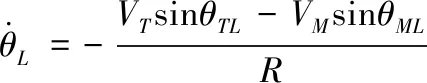
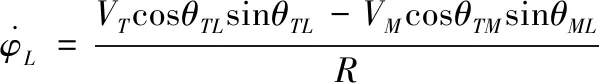

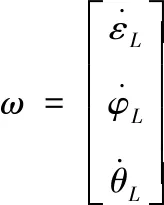
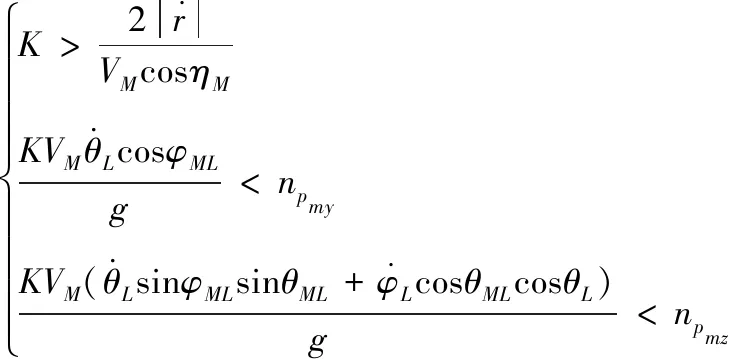
2.2 RBF神经网络制导律


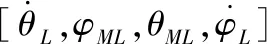
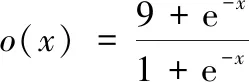

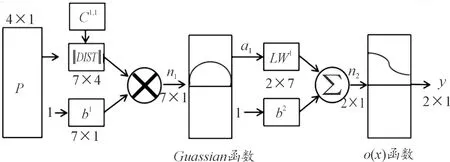
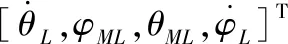
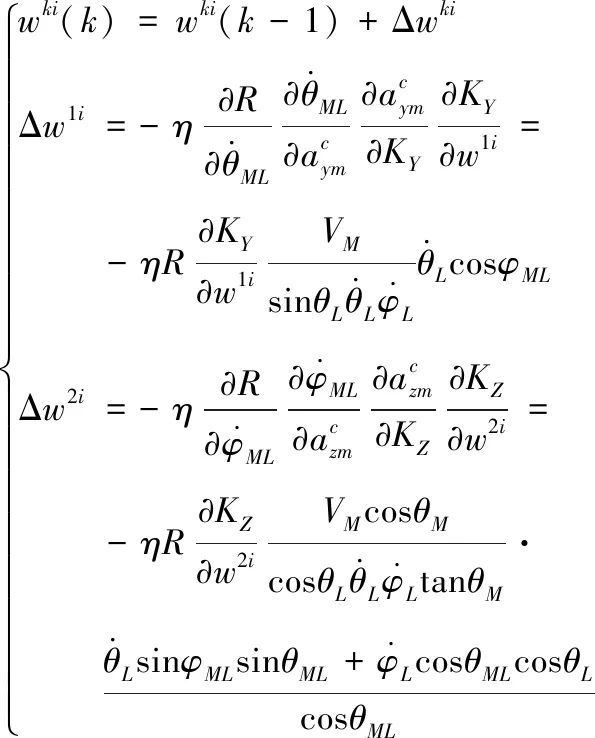
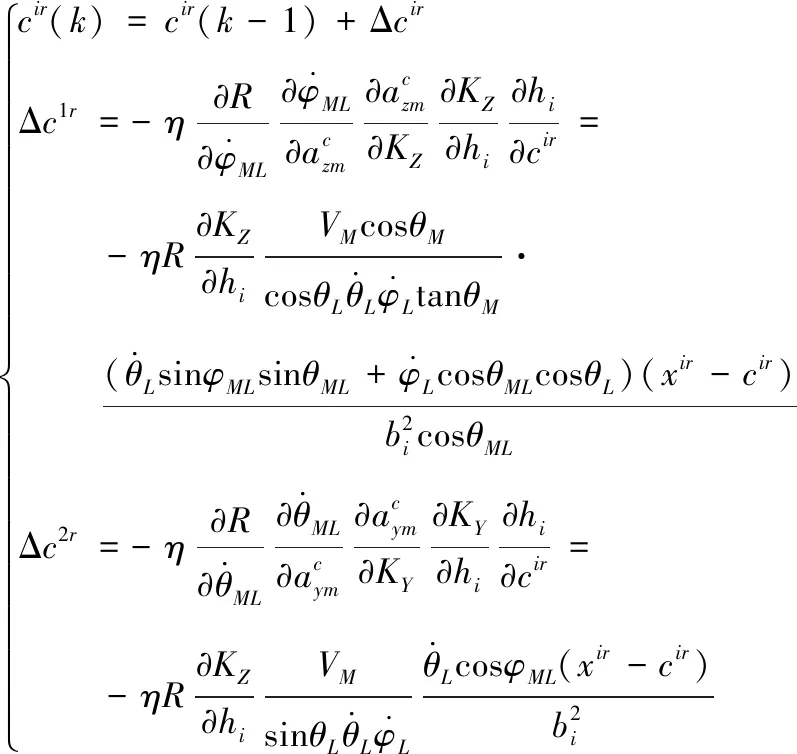
3 基于RBF神经网络的制导方法的仿真与分析



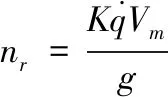

4 结论
