基于有限元法的带束层传递环夹持精度分析
2023-11-12杨慧丽
杨慧丽
(1. 青岛科技大学,山东 青岛 266045 ;2. 软控股份有限公司,山东 青岛 266045)
0 引言
随着高速公路的不断延伸和汽车工业的飞速发展,汽车速度在不断提高,特别是家庭轿车的普及[1]。在汽车用橡胶制品中60% 为轮胎,40% 为其他橡胶制品[2],因此人们对轮胎的认识也在不断提高, 对轮胎的品质也提出了更高的要求。
轮胎按照轮胎工艺不同基本可分为子午胎和斜交胎[3]。对于子午线轮胎不论是用何种成型工艺完成成型,在成型过程中都具备带束层的传递装置,即:成型机都有带束层胎面贴合筒的传递装置。带束层和胎面贴合筒占整个生胎重量的60% 以上[4],其夹持精度将影响轮胎成型的均匀性[5],最终影响到轮胎的品质。
在轮胎成型设备中用于传递带束层的装置被称为带束层传递环[6]。对于带束层夹持后变形量的测量工作在设备运动过程中难以实现,因此通过实验测量方法确定夹持精度无法较好地实现。有限元法是目前在工程领域常用的分析计算方法,由于其普遍性和有效性,在工程领域已得到广泛的认可[7],因此借助有限元法可有效的分析带束层夹持的变形量,从而判断其精度是否满足要求。
本文基于有限元分析方法,针对带束层传递环进行带束层夹持精度分析。按照传递装置的功能要求进行建模,分别针对带束层传递环空载工况及环体夹持带束层工况下环体的刚度及强度进行分析,得出优化的解决方案对于成型设备的性能提升具有重要意义。
1 有限元法理论
有限元的基本思想是将连续的计算域离散成有限个小的单元,这些单元以一定的方式进行相互连接代替连续体,然后运用数学工具求解该离散域的近似解,从而获得相应的求解结果[8]。由于近似解精度较高,因而被广泛用于设计人员解决工程实际问题。
1.1 有限元法数学实现
有限元法分析计算过程大致如下:
(1)结构离散化
将连续的几何模型划分为若干个离散的单元,并将这些单元通过单元节点按照模型实际的连接关系连接在一起,研究单元的平衡和变形协调,形成单元平衡方程。其中第i个节点的节点位移与节点外载荷有如下表达:
其{δi} 中表示第i节点的位移矩阵,{di} 与{θi}分别表示第i节点的位移分量;{Qi} 表示第i节点的外载荷矩阵,{Fi} 与{Mi} 分别表示第i节点的外载荷分量
(2)单元计算
通过节点位移与节点外载荷表达式,根据划分单元所包含的节点个数,通过单元刚度矩阵,建立单元节点力与单元节点位移的关系,单元刚度矩阵显示了计算单元的弹性特性。下面说明单元刚度矩阵与单元节点力及单元节点位移的关系:
单元内任意一点的位移表示为:
其中:
[W]— 位移参数矩阵;
{a}— 系数列阵。
由于单元节点的位置坐标已知,因此带入上式并求解单元节点位移矩阵为:
上式中[A] 为与该单元有关的系数矩阵,反解出(2) 式并带入(1) 式得:
其中[N]=[W][A]-1为形函数矩阵,通过形函数矩阵可得到单元内部任意位置的位移。
由弹性力学理论,单元内任意点的应变可表示为:
上式中:
[B]— 应变矩阵,通过弹性力学应变模式以及形函数求得。
根据广义胡克定律,由弹性关系物理方程即可求得单元应力:
上式中:
[D]— 弹性矩阵;
[D][B]— 应力矩阵
在任意节点的虚位移下,单元节点力所做虚功与单元内力所做虚功之和为零,依据虚功原理建立等式:
其中:
上三式中:
δAσ— 单元节点力虚功
δAσ— 单元内力虚功;
{δ*}T— 单元节点虚位移矩阵。
将式(7) 与(8) 带入式(6) 并整理得:
记为:
其中:
{F}e— 单元节点力矩阵;
{K}e— 单元刚度矩阵;
{δ}e— 单元节点位移矩阵。
(3) 整体计算
将连续体离散为若干个小单元,各单元之间通过节点相互连接,由于m 单元与n 单元之间相连接的节点有相同的位移,因此可通过单元计算结果对m 单元与n 单元的组装以形成整体模型的计算,最终得到外部载荷与整体模型节点位移的关系:
式中:
{F}— 载荷矩阵
{K}— 整体刚度矩阵
{δ}— 节点位移矩阵
通过(2.10) 计算整体节点位移,再通过节点位移计算单元应变应力,从而完成模型整体的计算分析。
1.2 有限元接触问题
利用有限元法分析工程实际问题时,接触问题普遍存在[9]。接触问题是一种高度非线性问题,在有限元法分析过程中常用的接触算法有罚函数法、Lagrange 乘子法[10]、增广Lagrange 法[11]等。对于Lagrange 乘子法,其解为精确解,但增加了计算变量,使方程性能变差,并且导入了零对角项,使方程变为非正定方程,计算难以收敛;对于增广Lagrange 法则需要迭代求解Lagrange 乘子,使计算量增加,增加计算成本。罚函数法计算为近似解,通过选取合适的惩罚因子可满足精度要求,同时其实现简单方便,计算量不大,完全满足接触计算需求。
对于罚函数法,其势能泛函J表示为:
上式中:
K— 弹性系数;
x— 物体位移;
F— 外力;
εN— 罚函数;
go— 接触穿透量。
除变形势能与外力做功外,由接触引起的能量增加应考虑进势能泛函中,其形式相当于在接触面两节点间施加弹簧,其中(x+go) 为弹簧变形量,罚函数为刚度系数。
对泛函J进行一阶变分,令一阶变分等于零求得泛函的极值条件:
由此得到:
由上式可看出,当足够大时,x越接近精确解go。
2 带束层传递环有限元分析
2.1 带束层传递环结构组成及功能
本文所分析用带束层传递环三维模型如图 1 所示,其主要包含环体、夹持气缸组件、瓦块组件、安全防护等组成。
带束层传递环的主要功能为:
(1)带束层传递环移动到带束层鼓贴合位,夹持气缸组件伸出,将瓦块组件推到贴合于带束层鼓上的二段胎冠上,带束层鼓收缩后,带束层传递环将二段胎冠抓取。
(2)将抓取的带束层传递环从带束层鼓贴合位移动到定型位。
(3)在成型鼓上的一段胎体充气定型时,为二段胎冠提供支撑,使一段胎体和二段胎冠结合,形成生胎。
(4)将成型结束的生胎从定型位移动到卸胎位。
2.2 空载状态有限元分析
有限元分析模型的建立过程主要包括:几何简化、零部件材料定义、接触关系设定、网格划分、施加载荷、设定约束及求解[6]。
2.2.1 有限元模型建立
为合理的减少计算量,需要对现有的几何模型进行简化,去除对整体结构刚度和强度影响较小的非关键部件的圆角、孔、凸台等特征,对夹持爪进行局部网格细化,整体网格划分如下图2 所示。
整体模型所使用材料为Q235B,材料屈服极限为235 MPa,弹性模型E=210 GPa,泊松比λ=0.274,材料密度ρ=7 830 kg/m3
对于环体的约束,由于环体下底座通过螺栓紧紧把合在下方安装座上,且分析关注位置主要在环体底座以上部分的结构,因此对环体底座下底面整个面上的自由度进行全约束处理。
结构所承受的载荷情况如下表1 所示:

表1 带束层环体分析所施加的载荷及相关参数
2.2.2 空载变形分析
为得到瓦块数对夹持环体刚度特性的影响,对夹持环体静力变形进行分析。分别建立夹持爪数量为5、6 和11 时的模型,分别对其进行分析。
夹持爪数量为5 时,环体整体变形情况如下图3所示。X、Y、Z方向的变形情况如下图 4 所示。
由整体最大变形量以及X、Y、Z方向的变形量可以看出,夹持环体变形的主要方向为Z方向,分析可以得到产生变形的原因为环体关于X-Y平面呈非对称结构,由于重力的作用而产生的变形。
夹持爪数量为6 时,环体变形情况如图 5 所示。X、Y、Z方向的变形情况如图6 所示。
同夹持爪数量为5 时变形结果类似,夹持爪数为6 时,变形也主要产生在Z方向,由于夹持爪数量增加会使重力作用产生的非对称分布更加明显,变形量较夹持爪数量为5 时更大。
夹持爪数量为11 时,环体变形情况如下图 7 所示。X、Y、Z方向的变形情况如下图8 所示。与夹持爪数量为5、6 时类似,变形主要发生在Z轴方向,并且变形数值也有所增加。
整理上述各项变形结果如表2 所示。
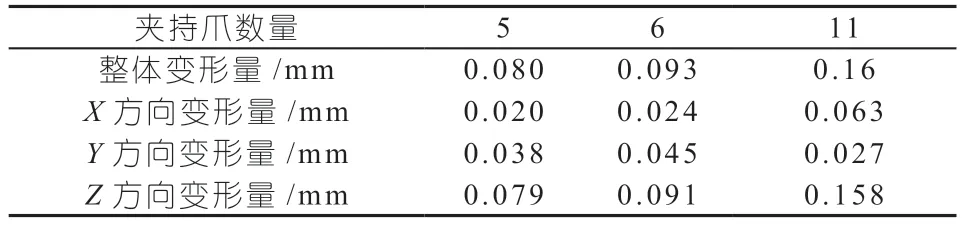
表2 空载工况环体整体及各方向变形量
分析上表可以看出,整体、X方向、Y方向、Z方向的变形均随着夹持爪数量的增加而增大,整体变形最大值发生在瓦块数量为11 时,环体的顶部,最大值为0.16 mm。分析瓦块数量为5 或6 时,最大值均发生在环体的顶部,主要由Y方向和Z方向的最大变形量均在环体的顶部决定。
Y方向的变形即为竖直方向的重力所引起的变形,最大变形量则定会发生在环体的顶部。由于此方向的变形是由重力所造成,所以可以通过对环体轻量化减小此方向的变形。即可以考虑在优化时将夹持爪支架和夹持爪采用铝材料。
Z方向的变形主要是由于环体结构不对称,在重力的作用下产生变形,而且Z方向是变形量最大的方向,通过结构优化减小Z方向的变形对减小整体变形十分必要。由于是由环体结构不对称引起的变形,可以通过增加配重,减小此变形量。
2.2.3 空载强度分析
为得到夹持环体强度特性,分别对夹持爪数量为5、6、11 的环体强度进行分析,得到应力云图结果如图9图10所示。
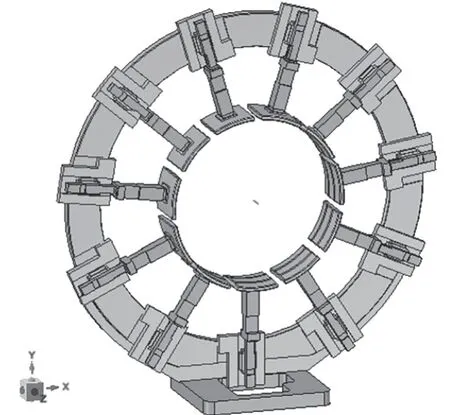
图1 带束层传递环三维模型

图2 环体网格划分
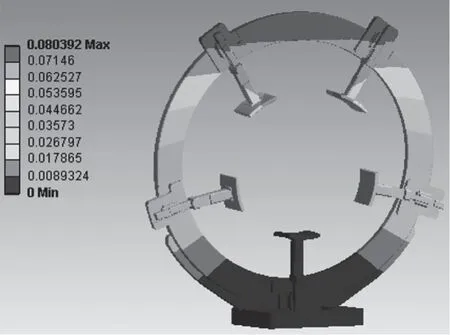
图3 夹持爪为5 整体变形
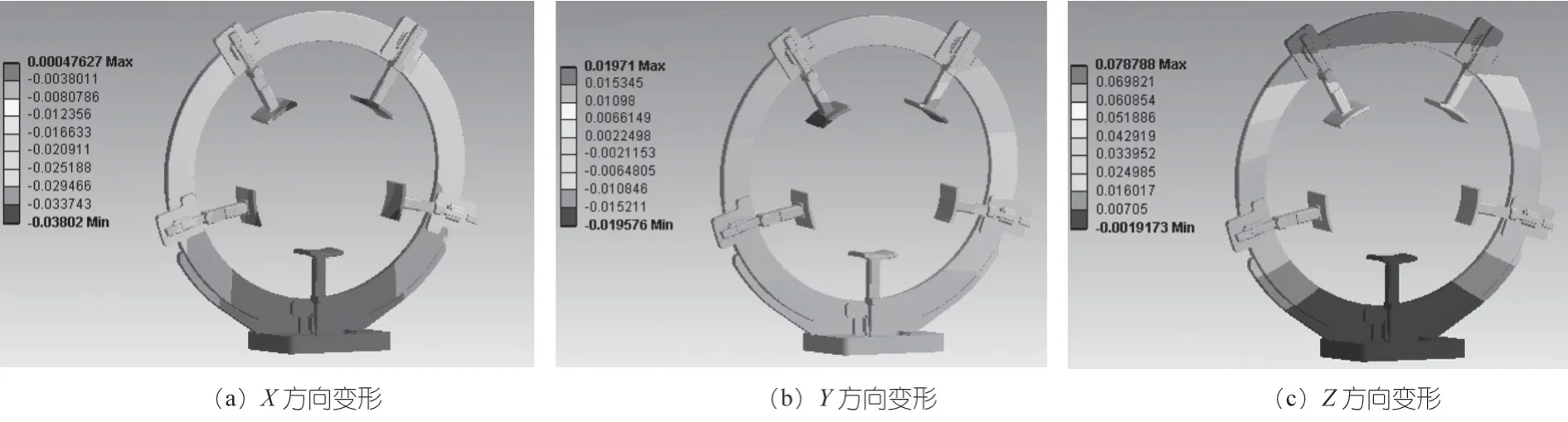
图4 夹持爪为5 时X、Y、Z 方向变形
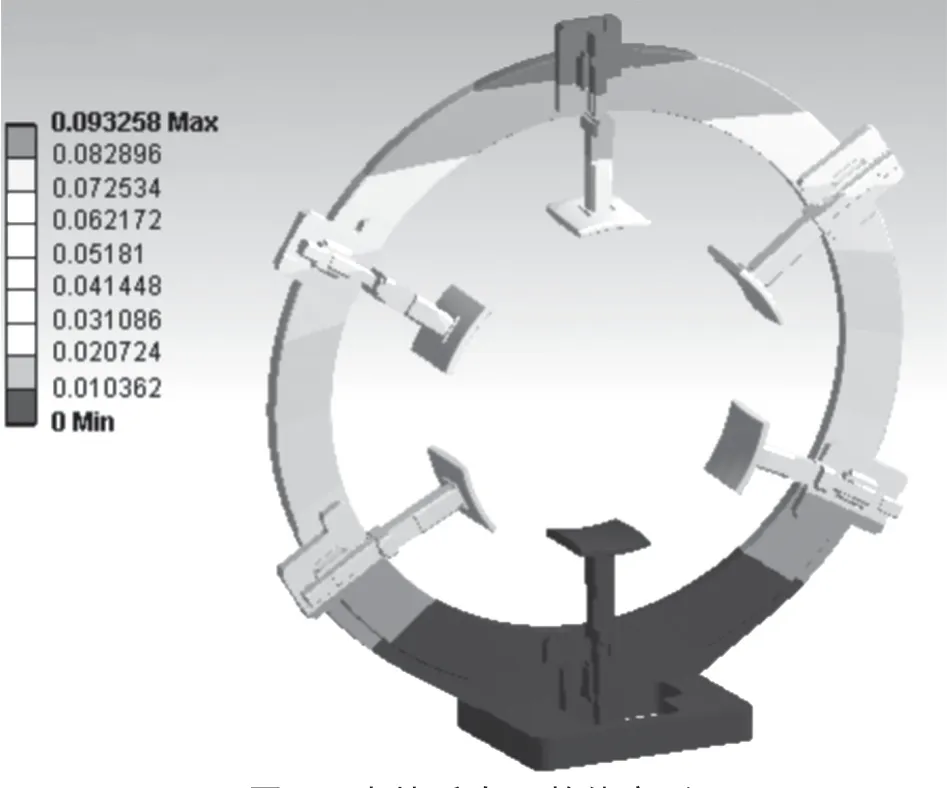
图5 夹持爪为6 整体变形
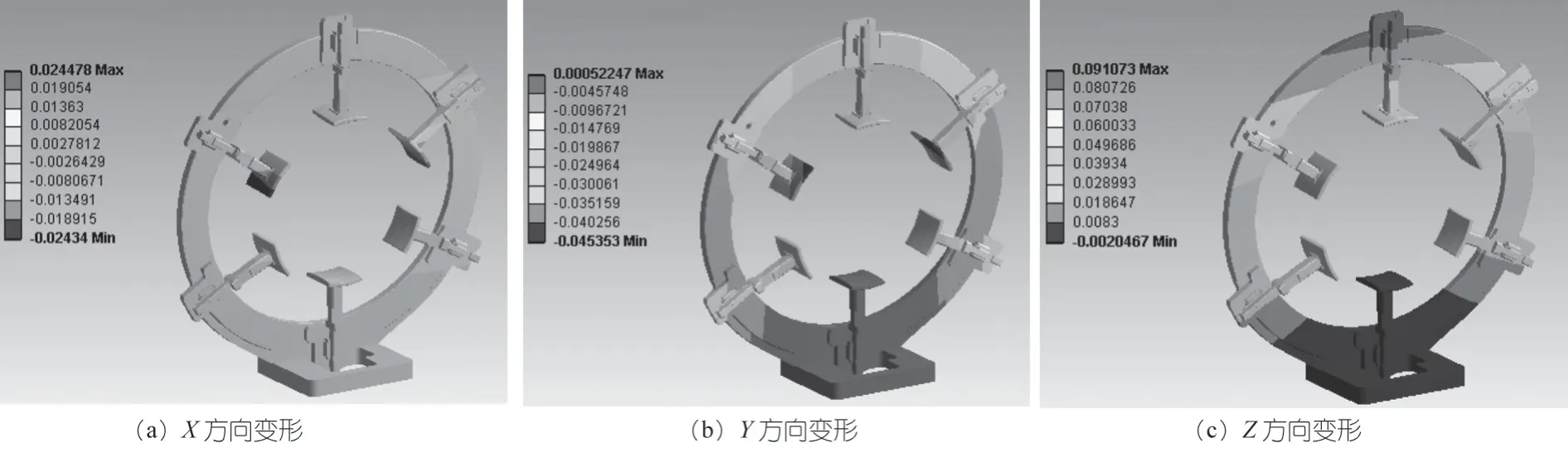
图6 夹持爪为6 时X、Y、Z 方向变形

图7 夹持爪为11 整体变形
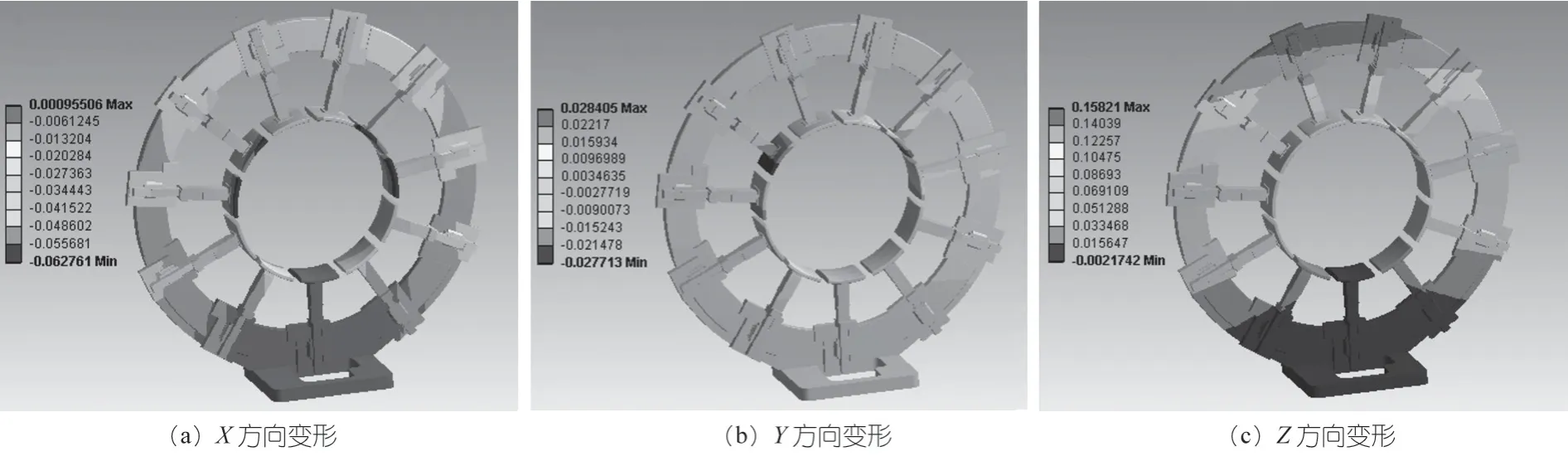
图8 夹持爪为11 时X、Y、Z 方向变形
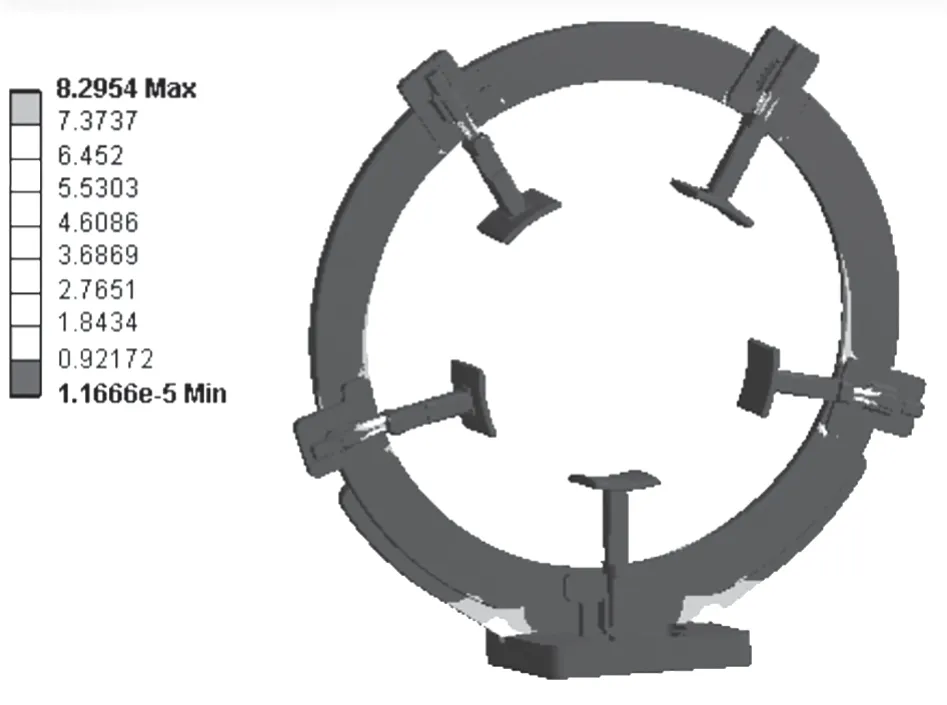
图9 夹持爪为5 环体应力
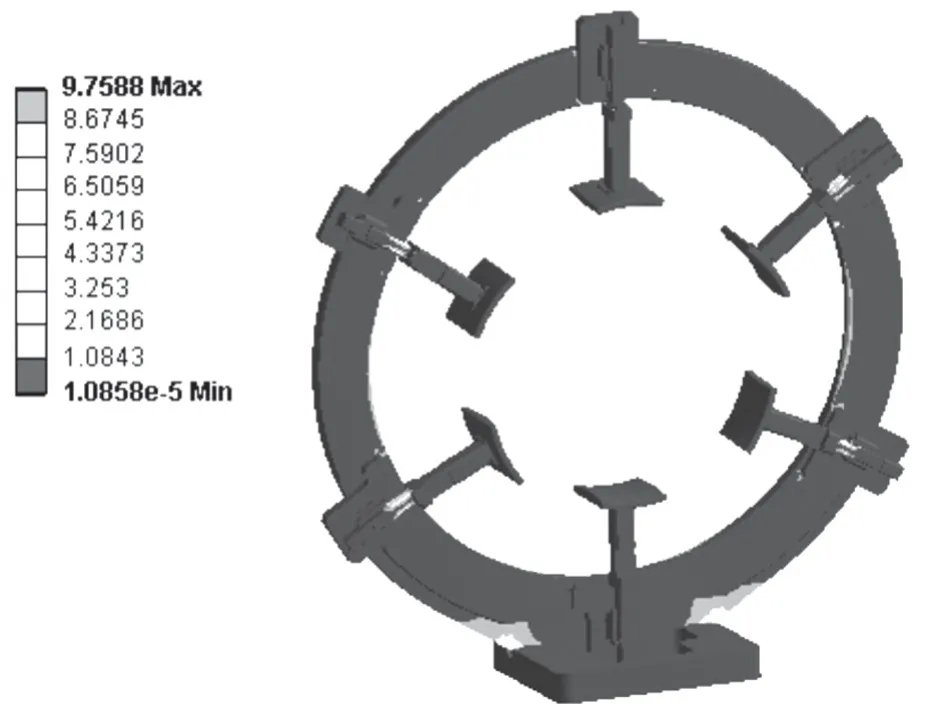
图10 夹持爪为6 环体应力
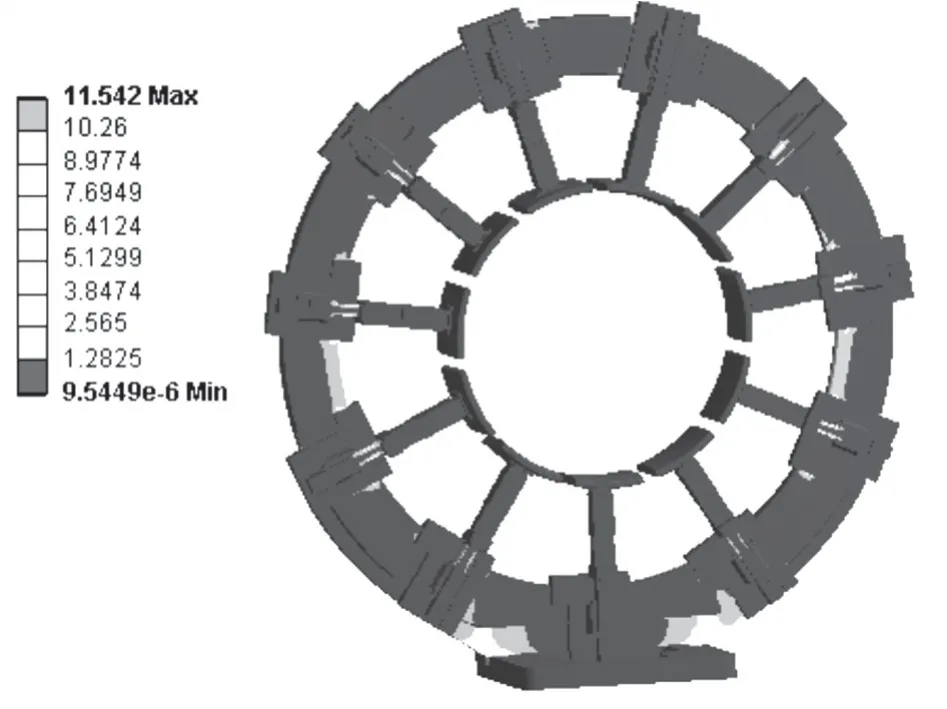
图11 夹持爪为11 环体应力
整理如上环体强度特性分析应力结果,分析得到表3。

表3 环体应力特性分析
由上表分析可以看出,随着夹持爪数量的增加,整体最大应力增加,但传递环整体结构应力水平较低,强度满足设计要求。
2.3 夹持状态有限元分析
2.3.1 橡胶材料本构
带束层是由多层带束胶布叠压而成,而带束线是由钢丝或尼龙线制成。这种结构使轮胎在承受车辆重量和承受路面压力时具有更好的刚性和稳定性。其中带束胶在轮胎成型前为未硫化橡胶,在进行带束层传递环夹持分析时,需要考虑带束层橡胶参数以获得更准确的计算数据。
未硫化橡胶具有典型的粘弹性特征[12],本文采用Prony 级数表示法来表示广义Maxwell 模型的粘弹性力学行为,其包含了剪切松弛模量与体积松弛模量。剪切松弛模量表示为:
体积松弛模量表示为:
其中,gi,ki,τG,τk为材料常数,通过试验获取,它们分别为Prony 级数的本构参数。由于橡胶属于体积不可压缩的材料,因此不需要定义体积的粘弹性行为。
2.3.2 有限元模型建立
由于夹持状态的模拟仅增加了带束层部分,因此环体的有限元模型参照空载状态有限元模型创建即可。带束层模型则考虑内部钢丝及胶料的模型创建,其中胶料以壳单元模拟,材料设置参考3.3.1 节橡胶材料本构输入参数;钢丝以梁单元进行模拟,按照内部钢丝角度进行详细建模。由于轮胎成型过程中钢丝始终处于线弹性范围内,因此钢丝材料属性为:弹性模量E=210 GPa,泊松比λ=0.3,材料密度ρ=7 850 kg/m3,建立好的带束层模型如图12,含带束层的整体有限元模型如图13。

图12 带束层网格模型

图13 含带束层夹持环体网格划分
对夹持爪及带束层进行局部网格细化,整体网格划分如图13 所示。
夹持爪与带束层模型之间建立contact 接触关系,接触方式参考2.2 节理论,定义摩擦系数为μ= 0.76
结构所承受的载荷情况如下表4 所示:

表4 带束层环体分析所施加的载荷及相关参数
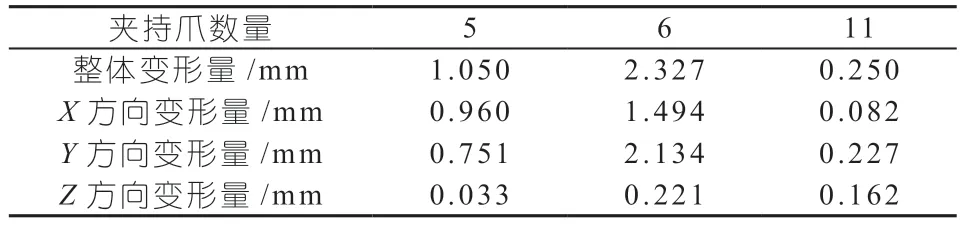
表5 夹持工况环体整体及各方向变形量
2.3.3 不同瓦块数夹持变形分析
针对带束层环体及带束层变形进行分析,对于带束层模型进行简化,由于无法得到准确的橡胶力学参数而采用近似橡胶的力学参数进行模拟。
为得到瓦块数对夹持环体刚度特性的影响,对夹持环体夹持变形进行分析。与静力变形相同,仍然建立夹持爪数量为5、6 和11 时的模型,分别对其进行分析。
对夹持爪数量为5 时,环体整体进行变形情况分析如下图14 所示。X、Y、Z方向的变形情况如图15所示。
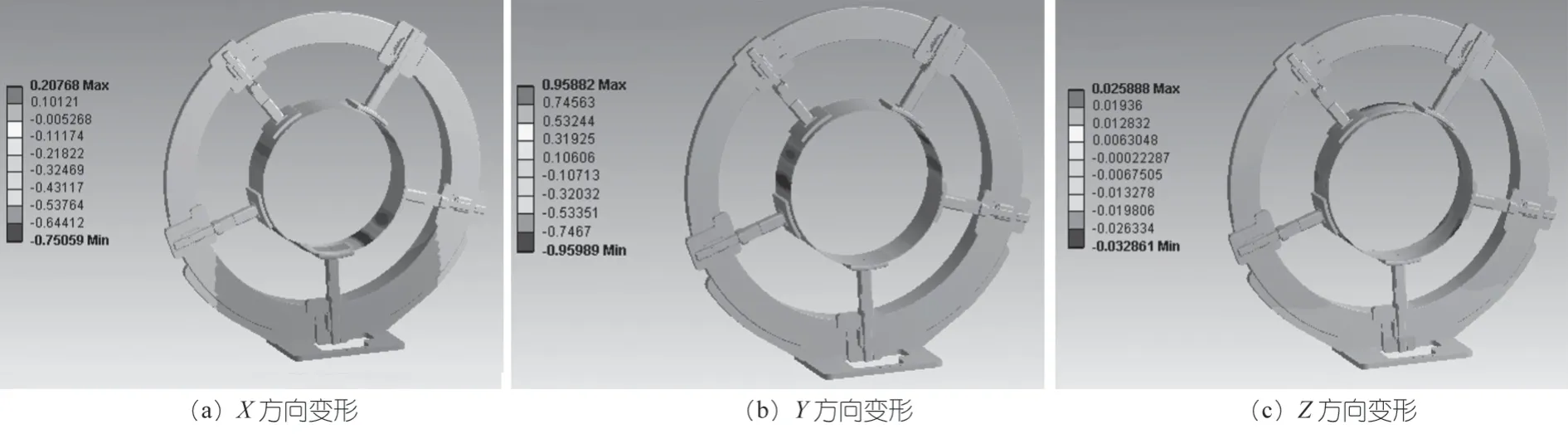
图15 夹持爪为5 时X、Y、Z 方向变形
夹持爪数量为6 时,环体夹持带束层变形情况如图16 所示。X、Y、Z方向的变形情况如图17 所示。
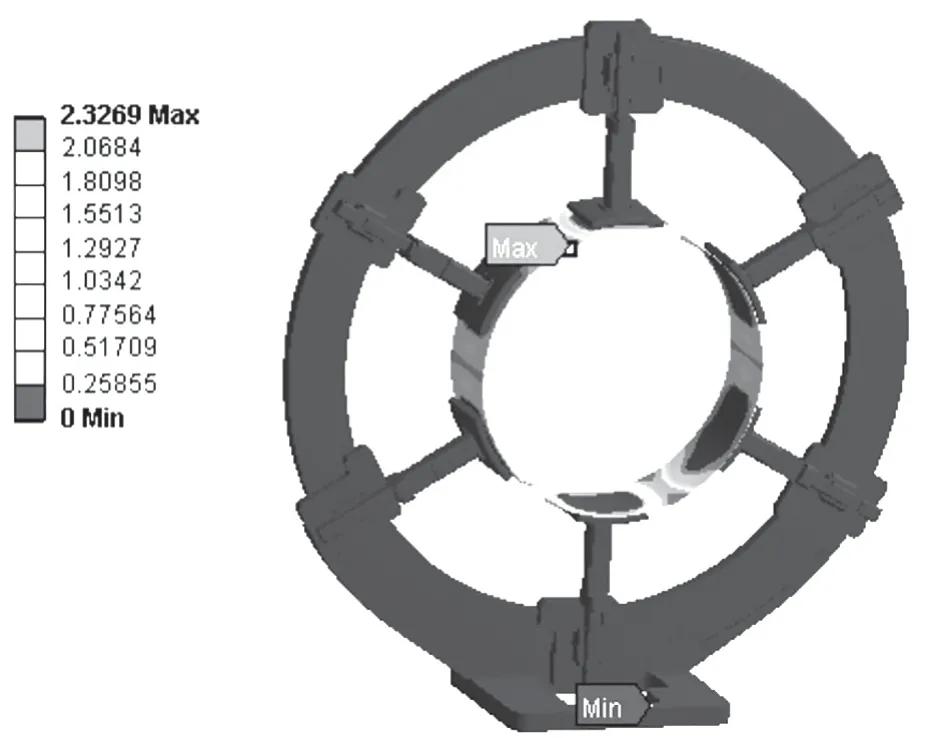
图16 夹持爪为6 整体变形
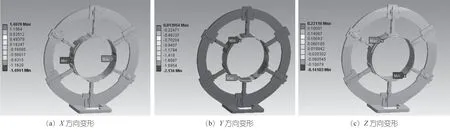
图17 夹持爪为6 时X、Y、Z 方向变形
夹持爪数量为11 时,环体夹持带束层变形情况如图18 所示。X、Y、Z方向的变形情况如图19 所示。
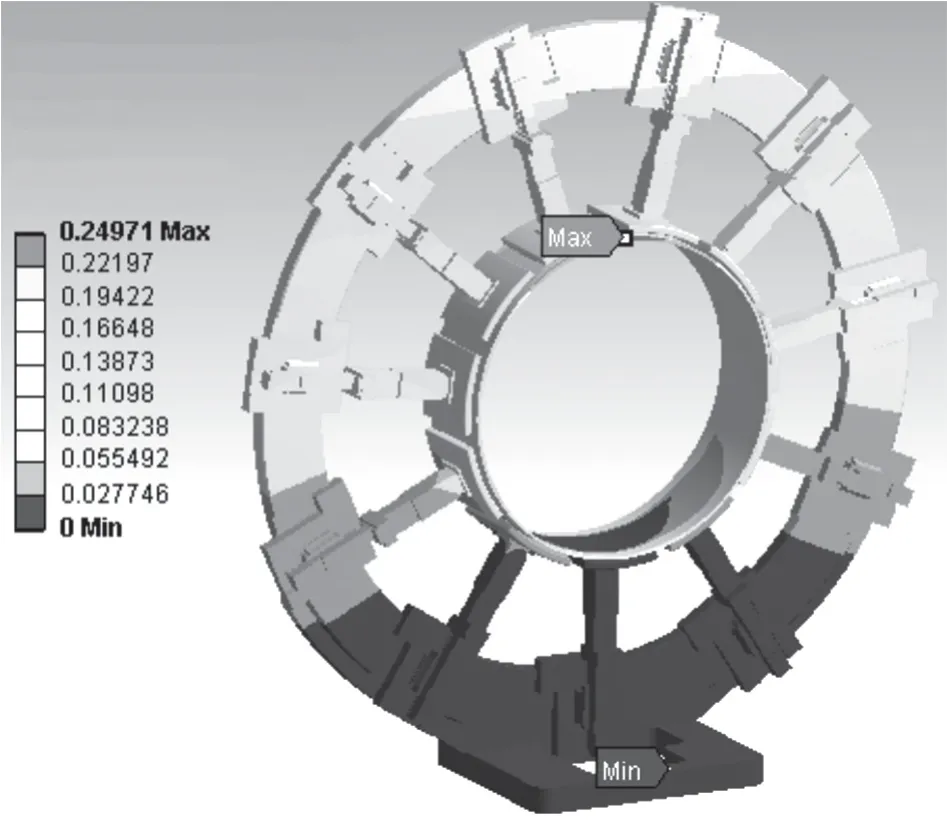
图18 夹持爪为11 整体变形
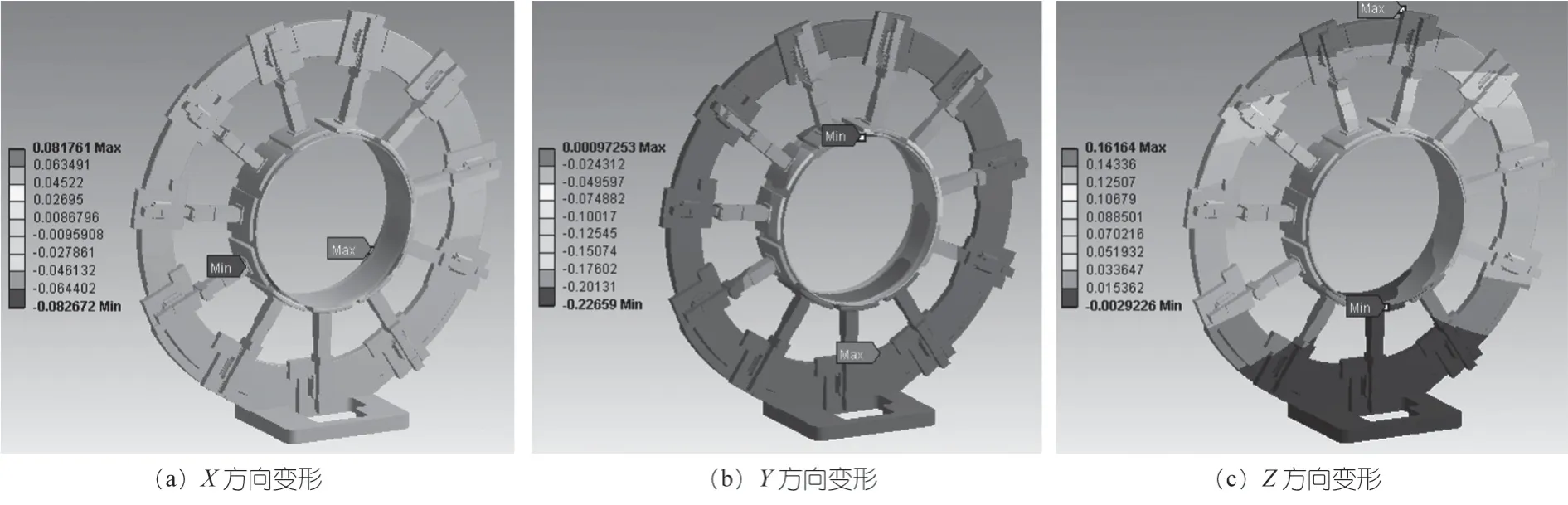
图19 夹持爪为11 时X、Y、Z 方向变形
综合以上结果可以得夹持装置最大变形量随夹持爪数量变化情况如下表所示。带束层最大变形量随夹持爪数量变化情况如下表 35 所示。
对比夹持带束层的夹持装置整体分析的结果,可以观察得到最大变形量都出现在带束层部分。分析整体变形量,随着夹持爪数量的增多带束层整体变形量有明显的减小。整体变形量数值由1.050 mm 减小到0.250 mm,变形主要发生在Y轴和Z轴方向,Y轴方向的变形主要是由重力引起,Z轴方向如同上文中分析所得,是由重力及环体结构的不对称分布引起。
Y轴方向的变形可以通过对环体结构的轻量化,对于夹持爪部分,可以采用铝制材料代替钢制材料。而对于Z轴方向的变形,可以改进环体结构,通过增加筋板作为配重,改善环体的不对称性,来减小Z轴方向的变形。
2.3.4 不同瓦块数夹持强度分析
为得到夹持环体夹持带束层强度特性,分别对夹持爪数量为5、6、11 的环体应力强度进行分析,得到结果如图20、图21、图22 所示。
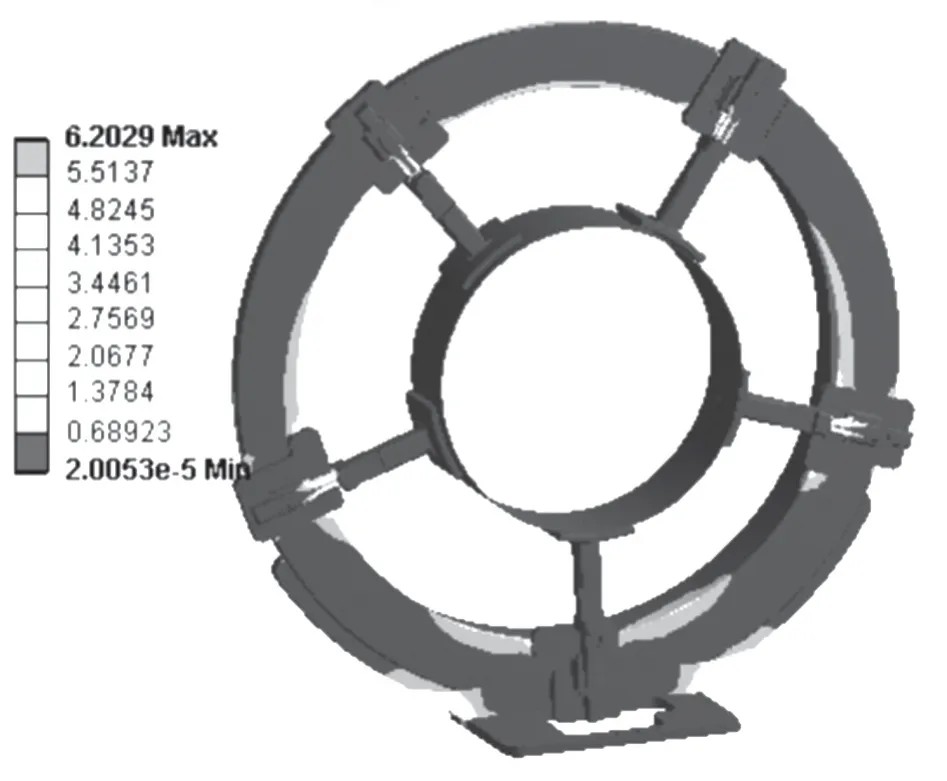
图20 夹持爪为5 环体应力
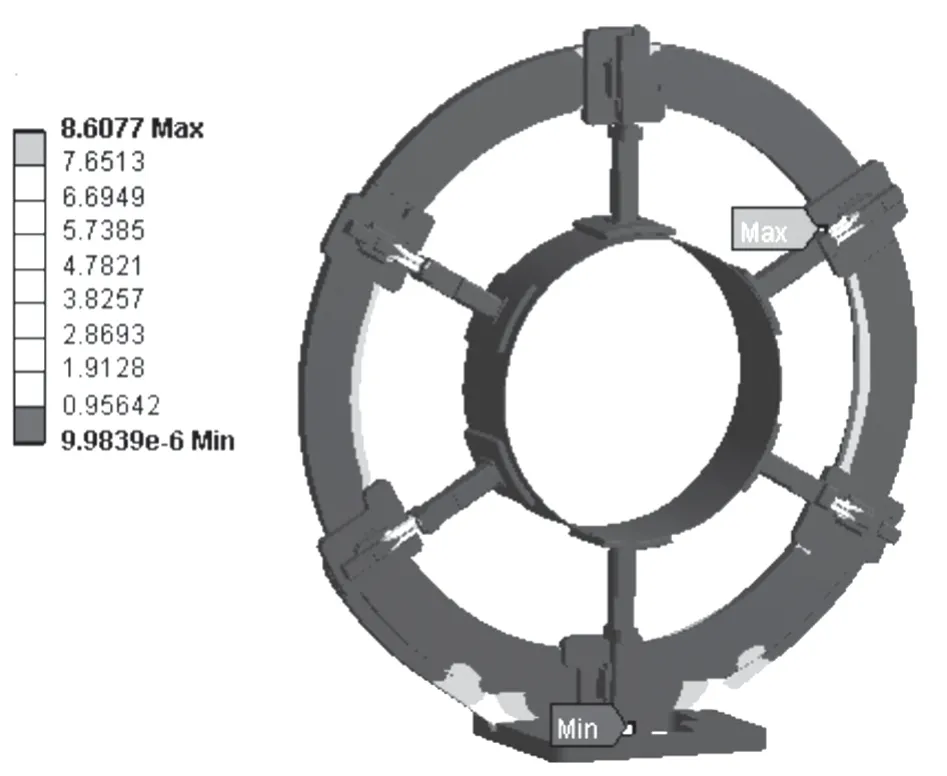
图21 夹持爪为6 环体应力
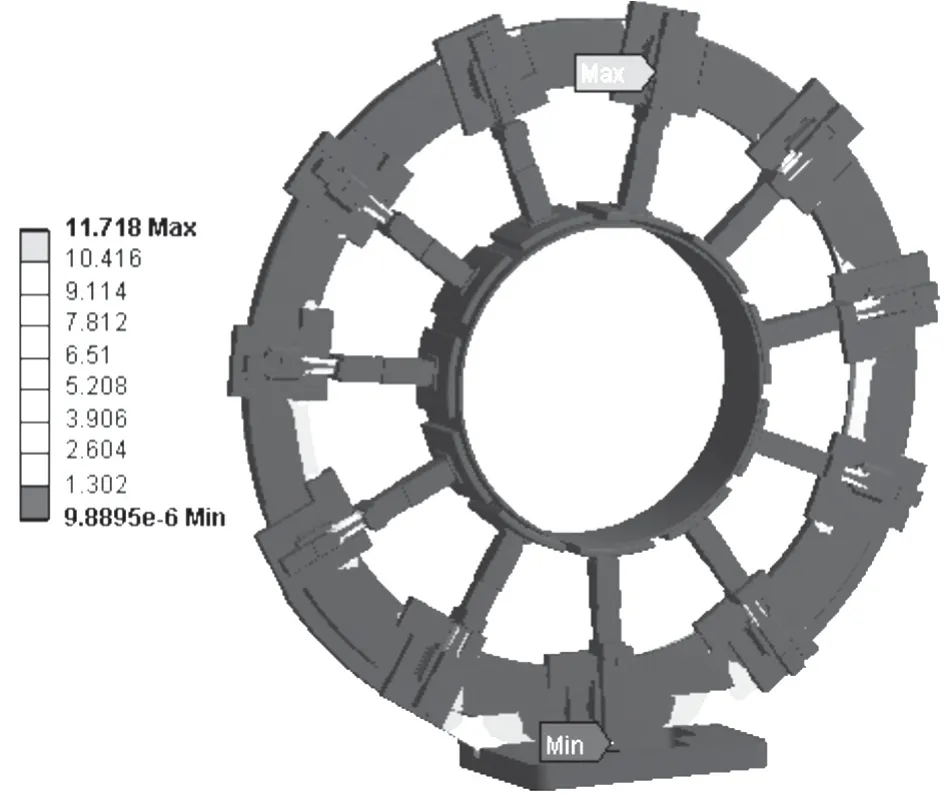
图22 夹持爪为11 环体应力
整理如上环体强度特性分析应力结果,分析得到表6。

表6 环体夹持带束层应力特性分析
由上表分析可以看出,随着夹持爪瓦块数量的增加,整体最大应力增加,但三种瓦块数量的传递环整体结构应力水平均较低,强度满足设计要求。
3 结论
本文通过有限元法对所设计轮胎成型设备带束层传递环进行详细分析,计算不同瓦块数下环体空载状态变形及强度,考虑环体本身对夹持精度的影响,以及计算不同瓦块数夹持带束层时的夹持精度。通过以上对带束层传递环装置刚度特性和强度特性的分析,可以看出:
(1)带束层传递环空载状态下本身变形量较小,强度满足设计要求,对带束层夹持精度影响较小。当增加夹持爪瓦块数量时整体应力和变形相对有所增加,但增量较小,完全满足设计需求。
(2)带束层传递环夹持状态下变形量较小,强度满足设计要求,同时对比5 瓦和6 瓦,环体采用11 瓦块夹持带束层时带束层变形量较小,因此采用11 瓦块方式夹持带束层对保证环体真圆度,减小环体变形,提高环体刚度均较5 瓦和6 瓦有较大提高。
(3)由于计算整体变形及应力处于较低水平,因此可用铝制材料瓦块代替钢制材料瓦块对环体进行轻量化,同时采用增加配重的方式改善由传递环不对称引起的变形,从而进一步对环体结构进行优化。
