面向存算一体芯片的非极大值抑制算法的量化部署＊

集美大学计算机工程学院 兰宝星 汤龙杨 吴仕龙 王世伟 黄斌

近年来，一种基于神经网络的非极大值抑制算法取得了媲美传统非极大值抑制算法的结果，并因其主要采用卷积算子和全连接算子而有望部署于存算一体芯片上。然而，目前以新型阻变存储器（RRAM）为代表的存算一体芯片大多只能支持5 比特以下的位宽，基于神经网络的非极大值抑制算法能否在低位宽的存算一体芯片上获取同等性能仍待研究。本文运用量化感知训练和后训练量化等方法，旨在探究低位宽对基于神经网络的非极大值抑制算法的影响。采用5 比特位宽的量化感知训练方法，在MS COCO 数据集的行人检测任务（Person Detection）数据集下，mAP 为62.71；在MS COCO 多类别（multi-class）检测任务下，mAP 和multiclass_ap 分别为40.66 和44.86，精度损失较小，为在低位宽存算一体芯片上部署目标检测算法奠定了基础。

在2008 年，惠普实验室发现了一种被称为记忆电阻器（或“忆阻器”）的新型电路元件，它可以通过电压调整掺杂物和无掺杂物的比例改变阻值。由忆阻器组成的交叉阵列可以根据欧姆定律和基尔霍夫定律实现大规模的矩阵乘法运算，因此适合于以密集矩阵运算为核心的神经网络算法。由交叉阵列和其他部件组成存算一体芯片的特点是可以组成具有计算能力的存储电路，进而真正实现“存储与计算一体”，这从根本上解决了冯诺依曼架构下大量的来回搬运数据导致的能量浪费问题。

存算一体芯片具有优于传统的存算分离芯片的能耗比优势。Aayush Ankit 等人研究了新型的存内计算芯片与传统的存算分离芯片两种不同方案的性能和功耗差异的对比，发现存内计算芯片相比于GPU 的能量消耗降低了10 ～50倍左右，吞吐量和单位能量下的算力也优于Google 公司的TPU 芯片[1]。Yao P 等人将图片分类网络完全部署至存内计算芯片中，其能量效率达到11.014TOP/s/W[2]。因此，存算一体芯片对于诸如目标检测的边缘端AI 应用具有巨大的意义，能够在理论上达到更高性能和更低功耗的目标。

传统的目标检测算法在部署到边缘端AI 芯片时，普遍采用CNN 网络的方法。CNN 网络通常以卷积运算为核心来提取图像中的信息，而卷积核在提取局部特征时会不可避免地出现冗余特征并可能产生多个候选目标框。因此，通常还需要使用非极大值抑制算法（Non-Maximum Suppression 或NMS）进一步消除冗余的候选目标框后才能得到最终的目标框。目前工业界常用的NMS 算法为贪心NMS 算法，但其算法实现是串行的，算法复杂度较高，无法部署至适用于密集矩阵运算的存内计算芯片，因此并不能满足在存算一体芯片上端到端部署的需求。

目标检测算法通常分为两个阶段：第一个阶段是提取图像特征并生成存在冗余的候选目标框（该阶段所采用的主干网络适合部署于存算一体芯片）；第二个阶段是用NMS 算法来去除冗余的目标框得到最终的目标框。如图1 所示展示了传统NMS 部署方式和基于存算一体芯片的NMS 部署方式的差异。目前工业界普遍使用的贪心NMS 不适合部署于存算一体芯片，因此需要通过a 方案中的传统AI 芯片（一般由Memory、CPU 和GPU 构成）完成处理。该类型处理器先将冗余目标框存储到Memory 中，CPU 从Memory 中读取数据并与GPU 交互进行数据处理，最后将处理的目标框保存到Memory，待数据处理完毕后输出目标框。在b 方案中，存算一体芯片先通过DAC 将数字信息转化为电信号，再通过忆阻器交叉对电信号进行计算得到结果，最后通过ADC 将输出的电信号转化为数字信息，最后输出目标框结果。

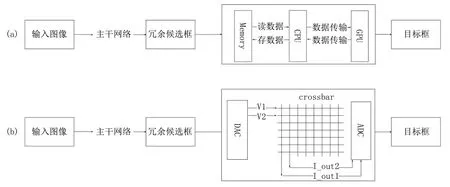
图1 传统NMS 和基于存算一体芯片的NMS 的差异Fig.1 Differences between traditional NMS and NMS based on compute-in-memory chip

J Hosang 等人提出了一种被称为“Learnable NMS”策略的GossipNet 网络[3]，采用神经网络学习每个候选目标框和其他候选目标框之间的特征关系，进而重新计算每个候选目标框的置信度。该网络核心在于通过对候选目标框进行特殊的算法处理，制作包含相邻候选目标框之间结构化特征关系的人工特征。GossipNet 网络再通过对人工特征进行学习和计算，得到每个候选目标框和其他候选目标框之间的特征关系。GossipNet 网络设计了一种能够惩罚“Double Detection”的损失函数，能够对多个检测框进行联合处理。实验表明“Learnable NMS”策略效果和Greedy NMS 算法相当，而且在某些情况下优于Greedy NMS 算法。由于GossipNet 的网络结构主要是基于密集矩阵运算，因而更加有利于部署在存算一体芯片架构上。但是，目前以新型阻变存储器（RRAM）为代表的存内计算芯片的单个忆阻器最多能支持5 比特的位宽，而传统的神经网络数据位宽通常是8～32 比特，所以如何在降低GossipNet 网络数据位宽的同时保持和原位宽较为接近的检测精度方法至关重要。

本研究面向基于神经网络的非极大值抑制算法在存内计算芯片上的量化部署展开，在Pytorch 框架上采用量化感知训练和后训练量化等方法，探究基于神经网络的非极大值抑制算法在存内计算芯片下超低位宽的表现。实验结果发现，对于MS COCO 数据集下的行人检测任务（Person Detection）数据集，采用5 比特量化的神经网络非极大值抑制模型取得mAP 为62.71；对于MS COCO多类别（multi-class）检测任务，采用5 比特量化的神经网络非极大值抑制模型取得的mAP 和multiclass_ap 分别为40.66 和44.86。这个性能比较接近全精度的版本，对于将Learnable NMS 部署到一个工业级的低位宽的存算一体芯片具有重要的指导意义。

1 相关工作

1.1 NMS

在目标检测中通常使用的是基于CNN 网络的目标检测算法，其通过卷积运算为核心来提取图像中的信息。基于CNN 网络的目标检测算法对同一个目标物体提取特征时，不可避免地出现冗余特征并可能产生多个目标候选框，此时就需要使用非极大值抑制算法的进一步处理，消除冗余的候选目标框后，才能得到最终的目标框。

常见的非极大值抑制算法分为两类：一类是无需学习的非极大值抑制算法，另一类是基于学习的非极大值抑制算法。在无需学习的非极大值抑制算法中，传统的Greedy NMS 算法基于一个固定的距离阈值进行贪婪聚类。具体而言，该算法会贪婪地选取得分高的检测结果，并删除那些与其重叠面积超过阈值的相邻结果，从而在召回率和精准率之间取得权衡。然而对于IoU 大于或等于NMS 阈值的相邻框，Greedy NMS 算法的做法是将其得分暴力置零，这使得该算法在处理存在遮挡的场景时表现不佳[4]。Bharat Singh 等提出了Soft NMS 方法，相较于传统Greedy NMS 算法会删除所有与最高分值的边界框大于IoU 阈值的框，该方法则采用降低这些框的置信度的方式进行处理[5]。Soft NMS 方法在处理低重叠的边界框时保留得更好。Chengcheng Ning 等人提出了一种名为Weighted NMS 的算法，该算法认为，传统的Greedy NMS 每次迭代所选出的最大得分框并非一定具备精确定位的特点，同时一些冗余的边界框也有可能具有良好的定位效果。因此，Weighted NMS 方法在处理过程中采用了与传统的直接剔除机制不同的策略，即对边界框的坐标进行加权平均，其中加权平均的对象包括得分最大的边界框自身以及与其IoU 大于或等于NMS阈值的相邻框[6]。Zheng Z 等人提出了DIoU-NMS 算法，该算法认为，若相邻框的中心点距离当前的最大得分框的中心点越近，则其更有可能是冗余框。该算法采用了DIoU 替代IoU 作为NMS 的评判准则。从直观的角度来说，加入了距离的信息，有利于在密集的场景中做更好的NMS[7]。Zheng Z 等人提出Cluster NMS，该方法主要旨在弥补Fast NMS 的性能下降，期望利用Pytorch 的GPU矩阵运算进行NMS，同时又使得性能保持与Greedy NMS相同，此外，笔者还在其中加入了很多其他操作，如得分惩罚机制(SPM)、加中心点距离(DIoU)、框的加权平均法(Weighted NMS)[8]。

关于基于学习的非极大值抑制算法，Hosang J 等人提出Conv NMS，其主要考虑到，如果将IoU 阈值设定得过高，则可能会导致抑制不够充分，而如果将IoU 阈值设定得过低，则有可能将多个真阳合并到一起。为了解决这个问题，其设计了一个卷积网络，将具有不同重叠阈值的Greedy NMS 结果进行组合，并通过学习的方法获得最佳的输出[9]。J Hosang 等人提出了Learnable NMS 方法，该方法主要考虑目标检测中遇到的高遮挡密集场景，通过联合相邻的预测框，向网络提供必要的信息，让网络能够确认一个物体是否被多次检测，并设计了一个损失函数来惩罚网络，使其学习到一个物体只生成一个高分预测框的特性。借助这个分数来达到NMS去重的目的，并使每个目标对应一个预测框。在PETS和COCO 数据集的高遮挡场景下，Learnable NMS 的AP 明显优于Greedy NMS，在高遮挡的场景下表现更好，并且GossipNet 非常适合处理各种类型的对象类[3]。Jiang B 等人提出了IoU-Net 方法，该方法提出了IoUguided NMS，即在NMS 阶段引入定位得分作为排序指标，而不是采用传统的分类得分。相较于Greedy NMS，该方法实际上就是用网络预测的IoU 替代了原来计算的IoU，Jiang B 等人认为，通过上述网络训练出来的IoU是包含了定位信息的，可以缓解冲突IoU 的定位信息缺失问题[10]。Liu S 等人提出Adaptive-NMS，该方法通过一个附属的网络来学习密集程度，根据密度值和阈值的对比实时修改NMS 的实现。该方法针对行人检测这一特殊的应用场景进行了优化，使得在人群密集的地方设置较大的NMS 阈值，而人群稀疏的地方设置较小的NMS 阈值[11]。

传统的Greedy NMS 并不适合部署在存算一体的芯片上，所以本研究在以存算一体芯片作为目标检测系统载体时，采用了一种被称为“Learnable NMS”的基于神经网络的非极大值抑制算法，该算法由J Hosang等人提出。与传统的Greedy NMS 不同的是，传统的NMS 依靠一个固定的阈值来删除那些IoU 过大且分数较低的预测框。而GossipNet 网络设计了一种能够惩罚“Double Detection”的损失函数，对多个检测框进行联合处理，且设计中不再出现IoU 的计算，有利于存算一体架构。

1.2 量化方面的研究

量化的目的是通过压缩神经网络中的参数数值位数，例如权重、激活值等，来实现对神经网络的压缩。不论是多值量化、三值量化还是二值量化，它们的核心操作都是将高精度的浮点数数值位数合理地压缩到低位的定点数数值位数，从而在减少网络性能的损失情况下，实现对模型的大幅度压缩。这种方式可以以很小的精度损失为代价，方便在边缘端上部署模型。

Gong 等人[12]采用向量量化来压缩深度卷积网络，该方法将权重分组且对各组的向量量化，从而减少权重数量。Wu 等人采用K-means 聚类量化的策略实现参数共享，从而实现不存储所有的权重值，而只是存储作为权重索引值的K 个质心，减少了模型大小[13]。Gupta 等人在基于随机舍入的CNN 训练中采用了16 位定点数表示，发现在几乎没有分类精度损失的情况下，采用低精度定点运算进行深度神经网络训练可以显著减少计算资源的使用和模型的内存占用[14]。Han 等人进一步提出了一种方法，基于权值共享对权值进行量化，然后使用剪枝和哈夫曼编码的方法，从而缩减模型大小[15]。Choi 等人证明了利用Hessian 权重来衡量网络权值重要性的可行性，并提出了一种聚类参数，用于最小化Hessian 加权量化误差[16]。

Vanhoucke 等人提出将权重值量化至8 位能够既保证最小的精度损失，又显著提升推理速度[17]。Jacob 等人提出一种关于在训练时保留32 位全精度存储方式，而在前向推理时对权重值与激活值进行8 位量化的量化框架，实现了整数算术的高效推理[18]。

Zhu 等人提出了8 位模拟的量化方法，为解决模拟量化时带来的不稳定因素影响和精度损失问题，该方法考虑到学习率对误差的敏感性，并通过对学习率进行调节和利用方向自适应的梯度阶段算法进行了解决[19]。

需要注意的是，二值神经网络是一种极端的网络量化方法。在一般情况下，网络模型的所有参数都以32 位单精度浮点数的形式存储，而二值网络中，参数和特征图激活值分别被量化为+1 和-1，每个值仅占用1 比特内存。

Liu 等人提出DSQ 方法，它是一种可微的软性量化策略，将全精度参数映射到低比特空间，并且保留了参数值的近似，能够通过在反向传播过程中获得更加精确的梯度来弥补二值网络在前向传播过程中出现的量化误差[20]。

Lin 等人提出一种对权重进行随机二值化处理的压缩方法，该方法不仅能够减少浮点运算次数，还具有一定的正则化效果，减小了精度损失[21]。

Zhang 等人提出一种可习得的量化器，将模型训练与量化器相结合，采取逐层优化量化策略，在训练过程中逐层优化量化模型，从而提升模型精度[22]。Cai 等人提出一种基于半波高斯量化的近似方法，在二值化权重的基础上，近似处理ReLu 激活函数，从而更好地完成二值化网络中的反向传播，减小精度损失[23]。

量化在目标检测领域内的应用也颇为深入。谷歌提出了一种8 位的量化方法[24]，显著提高了MobileNets[25]在ImageNet 分类[26]和COCO 目标检测[27]上的延迟和精度的权衡。Wei 等人提出了知识蒸馏和量化来对非常小的CNN 进行目标检测[28]。Zhuang 等人提出用全精度辅助模块训练低精度网络，以解决训练时梯度传播的困难[29]。Jacob 等人提出了一种仅用整数算子的量化方案，并在具有8 位精度的COCO 数据集进行目标检测[30]。Li 等人观察到在进行量化训练中进行微调的不稳定性，提出了三种方案[31]。然而，这些工作对网络结构和量化算法的设计都施加了额外的约束，从而限制了它们的性能。相比之下，Chen 等人提出了一种具有全整数算子操作的精确量化目标检测方案，完全摆脱了对浮点数的依赖。该方法用定点操作代替浮点操作，包括卷积层、归一化层和残差连接，从而实现了更好的性能[32]。目前还没有适合于目标检测算法的Learnable NMS 的量化方法研究。

2 技术方案

2.1 整体方案

为了达到在存算一体设备上超低功耗运行的目标，本研究需要在保持GoosipNet 网络效果的情况下尽可能地压缩网络参数，进而减少忆阻器的需求量，从而降低芯片尺寸和运行能耗。

在接下来的研究中将采用量化感知训练和后训练量化中的非对称量化对Learnable NMS 进行量化，以期在实际的模型部署到存算一体芯片前，GossipNet 网络在量化后的不同位宽下的表现中，分析出更好的优化方法以提高量化后的效果，达到和原网络相近甚至超过原网络的性能。

如图2 所示，可知Learnable NMS 和存算芯片的关系。图2 中Software 部分为Learnable NMS 核心的Block 部分，该Block 在GossipNet 网络中是一个序列，负责提取深层次的组合信息。

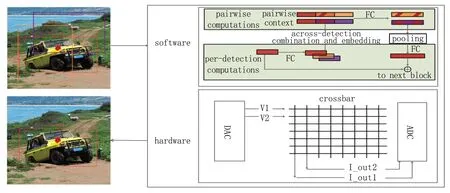
图2 Learnable NMS 在存算一体芯片上的部署Fig.2 Deployment of Learnable NMS on compute-in-memory chip

图2 中的Per-detection Computations 部分中，最左边的红色矩形框为Block 的输入，输入为0 矩阵或上一Block的输出，通过制作Pairwise Context 后，将上一个Block的输出先经过FC 整合，再提取出每一个预测框的相关信息，相邻预测框再从中取出和自己有关的信息和人工特征重新组合得到Pairwise Context，最后通过全连接层的映射和最大池化等操作完成深层次的组合信息地提取。

Block 序列输出的组合信息在GossipNet 网络中的全连接层中得到新的预测框分数。同时，网络期望每一个高分数的预测框都能匹配一个真实框。为了实现这个目的，网络通过损失函数惩罚将多个对应同一个目标的预测框中的其中一个设置为高分，其他设置为低分。这样，在高分匹配的同时，也实现了一个目标对应一个预测框这一目的，从而去除冗余的预测框。

图2 中Hardware 部分为存算一体芯片，通过DAC将数字信息转化为电信号，通过忆阻器交叉阵列对电信号进行计算得到结果，再通过ADC 将输出的电信号转化为数字信息，最后输出目标框结果。

2.2 量化感知训练

量化感知训练让网络在量化过程中进行训练，从而让网络参数能更好地适应量化带来的信息损失。在对Learnable NMS 进行量化感知训练时，本研究使用了Round 函数，但该函数无法进行训练，因为其几乎每一处的梯度都为0，导致反向传播的梯度也变成 0。因此，本研究采用STE 方法[33]，直接将卷积层的梯度回传到之前的权重上，以完成网络权重的更新，使得量化训练可以正常进行。

如图3 所示，STE 核心的思想就是权重参数初始化为Float，并将权重经过将原来的连续的参数映射成整数带入到网络进行前向传播计算，从而计算网络的输出。在反向传播时，直接对原来权重中的Float 参数进行更新，从而完成对整个网络的更新。通过这样的方式，就可以更新权重，使量化训练可以正常进行。

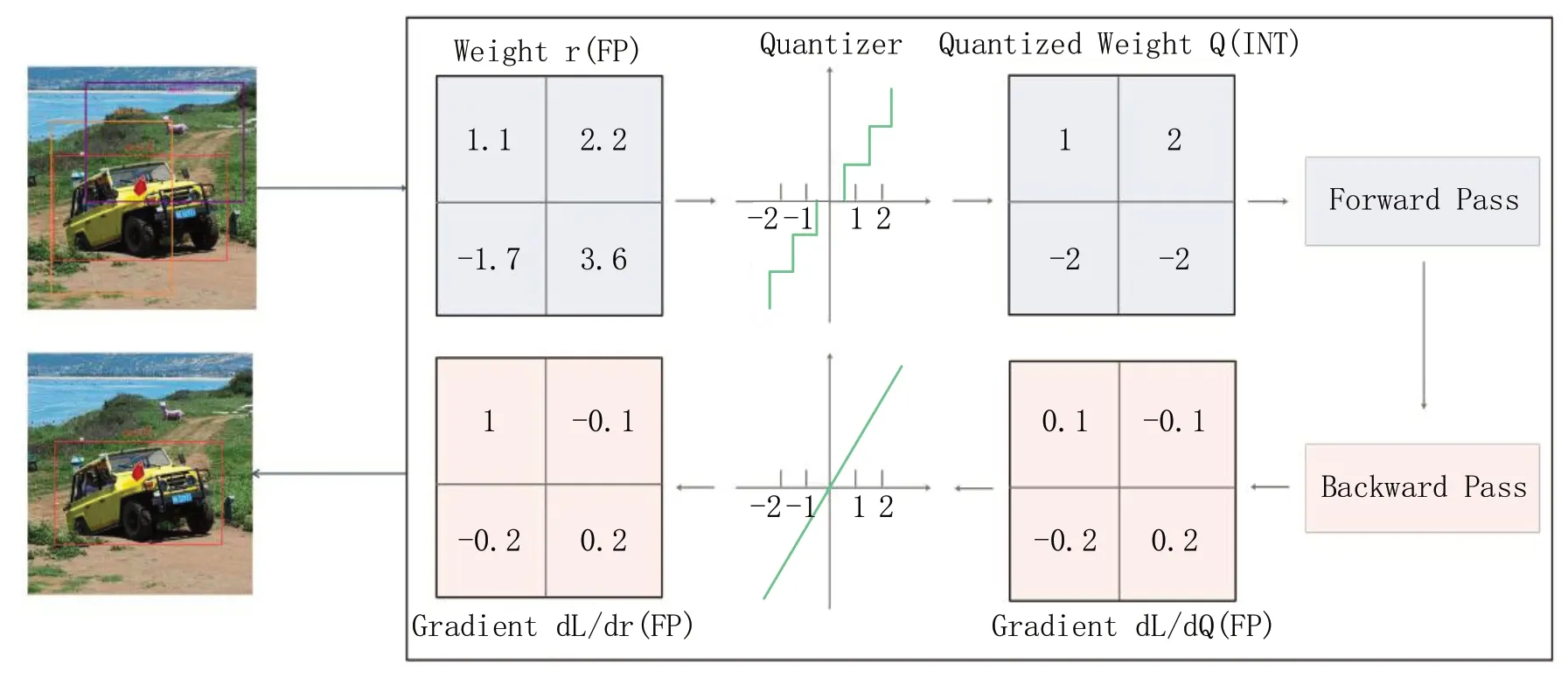
图3 Learnable NMS 的量化感知训练示意图Fig.3 Schematic diagram of quant aware training for Learnable NMS

简单而言，因为量化之后的数据是一个离散的方程，我们无法计算它的导数，所以STE 方法的目的就是在反向传播时绕过量化函数，使得梯度能够顺利地从输出层传递到输入层，简单粗暴地直接把输出的导数作为了对输入的导数，其前向传播和反向传播的相关关系如式（1）、式（2）所示：

其中，式（1）中表示本研究中将浮点数量化映射成整数的范围，式（2）表示使用在梯度更新时的因为量化函数无法求导，而使用近似估计来进行梯度更新的一种数学方法。

2.3 后训练量化

后训练量化即在不重新训练网络的情况下，获取已训练好的模型，将其训练过的32bit 神经网络直接转换为定点计算的网络。

以均匀量化中的非对称量化为例，根据如式（3）、式（4）、式（5）所示放缩关系来对Learnable NMS 后训练量化。

其中，式（3）计算了量化前的浮点数映射到量化后的定点数时的比例关系xscale，、分别表示量化前的浮点数的最大值和最小值，、表示量化后定点数的最大值和最小值，式（4）中表示0 经过量化对应的定点数，称作零点，式（5）表示量化后定点数的值。

3 实验设计

3.1 实验运行环境

本实验硬件采用GPU 型号为G200eR2，CPU 采用6核E5-2603 v3，频率为2.60GHz，软件配置采用Linux系统，在Pytorch1.9.1 框架、CUDA10.2 等基础上完成实验。Pytorch1.9.1 框架拥有强大的深度学习处理包，是进行模型量化时的一个很好的选择。

3.2 实验方法

首先，本次研究采用COCO 数据集进行实验，用于训练目标检测模型的子集COCO_2014_train 训练集进行训练得到模型，再采用量化中的量化感知训练和后训练量化操作将模型进行量化。

然后，本研究分别采用量化感知训练和后训练量化中的非对称量化方法。在实验中，对单独的COCO 数据集中的coco_person 类别和coco_muticlass 分别进行测试，在测试过程中，通过设定block=16，以mAP、multiclass_ap为评价指标，探究在block 等于16 下，GossipNet 网络在不同位宽（bit=8、7、6、5、4、3、2）的表现。

最后，本研究再将训练量化好的模型在COCO 数据集中包含80 个类别的物体子集coco_2014_minival 测试集上进行测试。随着位宽的减少，统计mAP 和multiclass_ap 的性能损失。

3.3 基于COCO:Person Detection 模型的量化

本实验对coco_person 这个类别进行量化感知训练，对GossipNet 网络分别进行量化位宽为8bit、7bit、6bit、5bit 量化感知训练。对于4bit 及4bit 以下的位宽采取后训练量化的策略，经过多次迭代量化，可以得到对应不同位宽的模型在测试集上测试得到的量化感知训练和后训练量化下最佳的性能效果的结果。

如图4 所示为量化感知训练与后训练量化在位宽为8bit 至5bit 的量化性能对比，由图4 可知，对GossipNet进行量化感知训练后，位宽为6 ～8bit 的性能表现甚至超过原网络的性能，而5bit 的性能相较原网络的性能只出现了微小的性能损失。但是后训练量化在5 ～8bit 的位宽下相较原网络的性能损失较大，且量化后性能表现与量化感知训练方法相比表现较差。因为4bit 及4bit 以下的位宽容易出现量化感知训练失效的情况，所以对于4bit 及4bit 以下的位宽，本研究基于16bit 预训练模型进行后训练量化。

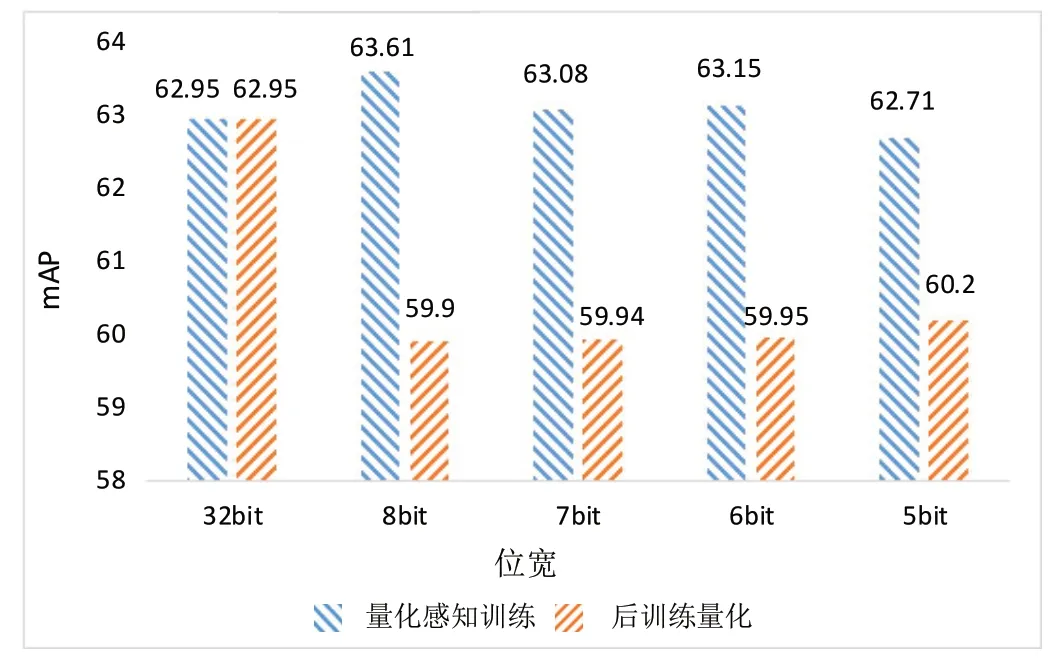
图4 量化感知训练与后训练量化最佳性能表现的对比Fig.4 Comparison of performance between quantizationaware training and post-training quantization for optimal quantized performance

如图5 所示，基于量化感知训练的16bit 模型再进行后训练量化得4bit 和3bit 的表现相较于原网络性能损失较大，在2bit 的位宽下，相较原网络性能损失了约40%。结合图4 和图5 可知量化感知训练和后训练量化相结合的量化策略，在3bit 及3bit 以上都有较为不错的表现。

图5 基于16bit 预训练模型后训练量化的性能表现Fig.5 Performance of post-training quantization based on 16-bit pretrained models

3.4 基于COCO:multi-class 模型的量化

本研究对COCO_muticlass 进行量化感知训练，并在coco_2014_minival 的测试集上进行测试。本实验对multi-class 进行量化感知训练，对GossipNet 网络分别进行量化位宽为8bit、7bit、6bit、5bit、4bit 量化感知训练。对于3bit 及3bit 以下的位宽采取后训练量化的策略，经过多次迭代量化，可以得到对应不同位宽的模型在测试集上测试得到的量化感知训练和后训练量化下最佳的性能效果的结果。

如图6 所示，随着位宽降低，量化感知训练的mAP性能表现在5bit 及5bit 以上的位宽下优于后训练量化。且相较于原网络性能而言损失较小，性能较为接近，但是在4bit 时量化感知训练，已经出现了大幅度的精度损失，而后训练量化在4bit 时效果明显优于量化感知训练。因为3bit 及3bit 以下的位宽容易出现量化感知训练失效的情况。所以对于3bit 及3bit 以下的位宽，本研究采取后训练量化。

图6 量化感知训练与后训练量化mAP 最佳性能表现的对比Fig.6 Comparison of performance between quantizationaware training and post-training quantization for mAP optimal performance

如图7 所示，后训练量化在3bit 时，相较于原位宽精度损失较大，在2bit 时性能损失相较于原网络损失了约50%。

图7 后训练量化在3bit 至2bit 下mAP 的性能表现Fig.7 Performance of post-training quantization for mAP at 3-bit to 2-bit levels

如图8、图9 所示，随着位宽的降低，从8bit 至4bit 量化后的网络精度相较于原位宽，出现了较小的精度损失。量化感知训练的multiclass_ap 性能表现在8bit 至5bit 时要优于后训练量化，而在4bit 时前者效果则弱于后者。在3bit 和2bit 下的性能表现也明显弱于原网络效果。

图8 量化感知训练与后训练量化multiclass_ap 最佳性能表现的对比Fig.8 Comparison of performance between quantizationaware training and post-training quantization for multiclass_ap optimal performance

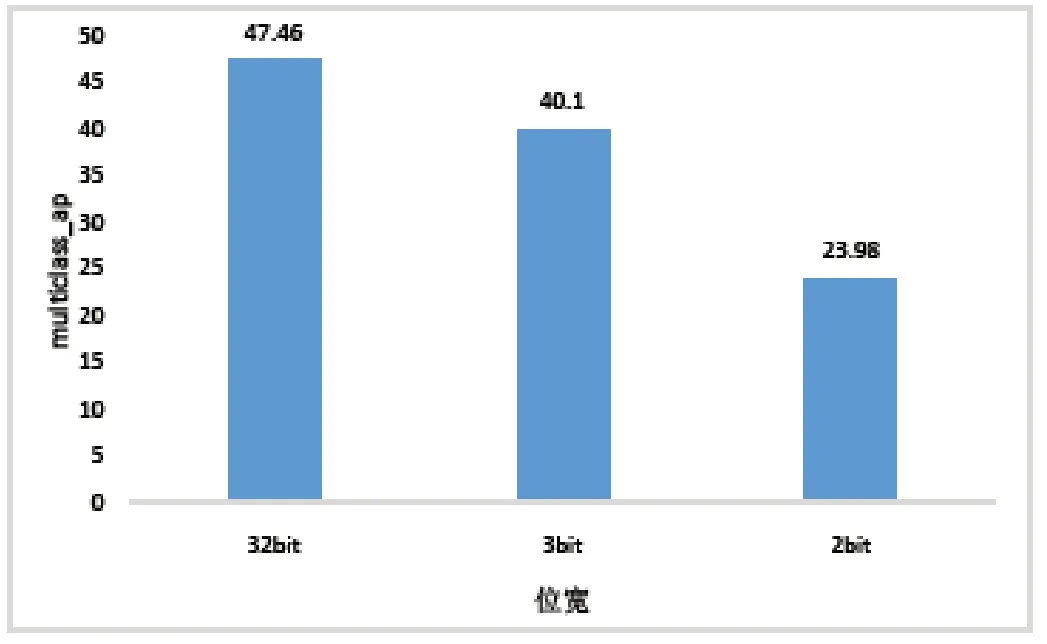
图9 后训练量化在3bit 至2bit 下multiclass_ap 的性能表现Fig.9 Performance of post-training quantization for multiclass_ap at 3-bit to 2-bit levels

4 结论

本研究通过对GossipNet 网络进行量化感知训练和后训练量化，发现在量化为5bit 及5bit 以上的位宽时，可以获得较好的性能表现。在基于COCO 的Person Detection 模型的量化中，5bit 及5bit 以上的位宽的量化感知训练结果性能损失都较小，甚至在6bit 及6bit 的量化感知训练中得到的性能效果略优于原网络。而在基于COCO multi-class 模型的量化中，5bit 及5bit 以上的效果性能损失较小，与原网络性能相近，而从4bit 开始，性能损失则较大。本研究表明，通过运用模型量化的手段，分别对Learnable NMS 进行量化感知训练和后训练量化，探究了GossipNet 网络在不同量化方式和不同位宽场景下的具体表现，从而为面向最多只能支持5bit 位宽的新型阻变存储器（RRAM）为代表的存算一体芯片部署提供了关键依据。

引用

[1] ANKIT A,HAJJ I E,CHALAMALASETTI S R,et al.PUMA:A Programmable Ultra-efficient Memristor-based Accelerator for Machine Learning Inference[C]//Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems,2019:715-731.

[2] YAO P,WU H,GAO B,et al.Fully Hardware-implemented Memristor Convolutional Neural Network[J].Nature,2020,577(7792):641-646.

[3] HOSANG J,BENENSON R,SCHIELE B.Learning Nonmaximum suppression[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,2017:4507-4515.

[4] GIRSHICK R.Fast r-cnn[C]//Proceedings of the IEEE International Conference on Computer Vision,2015:1440-1448.

[5] BODLA N,SINGH B,CHELLAPPA R,et al.Soft-NMS-improving Object Detection with one Line of Code[C]//Proceedings of the IEEE International Conference on Computer Vision,2017:5561-5569.

[6] NING C,ZHOU H,SONG Y,et al.Inception Single Shot Multibox Detector for Object detection[C]//2017 IEEE International Conference on Multimedia & Expo Workshops (ICMEW),IEEE,2017:549-554.

[7] ZHENG Z,WANG P,LIU W,et al.Distance-IoU Loss:Faster and Better Learning for Bounding Box Regression[C]//Proceedings of the AAAI Conference on Artificial Intelligence,2020,34(07):12993-13000.

[8] ZHENG Z,WANG P,REN D,et al.Enhancing Geometric Factors in Model Learning and Inference for Object Detection and Instance Segmentation[J].IEEE Transactions on Cybernetics,2021,52(8):8574-8586.

[9] HOSANG J,BENENSON R,SCHIELE B.A Convnet for Nonmaximum Suppression[C]//Pattern Recognition:38th German Conference,GCPR 2016,Hannover,Germany,September12-15,2016,Proceedings 38.Springer International Publishing,2016:192-204.

[10] JIANG B,LUO R,MAO J,et al.Acquisition of Localization Confidence for Accurate Object Detection[C]//Proceedings of the European Conference on Computer Vision(ECCV),2018:784-799.

[11] LIU S,HUANG D,WANG Y.Adaptive nms:Refining Pedestrian Detection in a Crowd[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition,2019:6459-6468.

[12] GONG Y,LIU L,YANG M,et al.Compressing Deep Convolutional Networks Using Vector Quantization[J].2014.

[13] WU J,LENG C,WANG Y,et al.Quantized Convolutional Neural Networks for Mobile Devices[C]//Proceedings of the IEEE conference on computer vision and pattern recognition,2016:4820-4828.

[14] GUPTA S,AGRAWAL A,GOPALAKRISHNAN K,et al.Deep Learning with Limited Numerical Precision[C]//International Conference on Machine Learning.PMLR,2015:1737-1746.

[15] HAN S,MAO H,DALLY W J.Deep Compression:Compressing Deep Neural Networks with Pruning,Trained Quantization and Huffman Coding[J].2015.

[16] CHOI Y,EL-KHAMY M,LEE J.Towards the Limit of Network Quantization[J].2016.

[17] VANHOUCKE V,SEN0R A,MAO M.Improving the Speed of Neural Networks on CPUs[J].Proc Deep Learning and Unsupervised Feature Learning Workshop,2011:1-8.

[18] JACOB B,KLIGYS S,CHEN B,et al.Quantization and Training of Neural Networks for Efficient Integer-arithmetic-only Inference[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,2018:2704-2713.

[19] ZHU F,GONG R,YU F,et al.Towards Unified Int8 Training for Convolutional Neural Network[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition,2020:1969-1979.

[20] GONG R,LIU X,JIANG S,et al.Differentiable Soft Quantization:Bridging Full-precision and Low-bit Neural Networks[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision,2019:4852-4861.

[21] LIN Z,COURBARIAUX M,MEMISEVIC R,et al.Neural Networks with Few Multiplications[J].2015.

[22] ZHANG D,YANG J,YE D,et al.Lq-nets:Learned Quantization for Highly Accurate and Compact Deep Neural Networks[C]//Proceedings of the European Conference on Computer Vision(ECCV),2018:365-382.

[23] CAI Z,HE X,SUN J,et al.Deep Learning with Low Precision by Half-wave Gaussian Quantization[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,2017:5918-5926.

[24] KRISHNAMOORTHI R.Quantizing Deep Convolutional Networks for Efficient Inference:A whitepaper[J].2018.

[25] HOWARD A G,ZHU M,CHEN B,et al.Mobilenets:Efficient Convolutional Neural Networks for Mobile Vision Applications[J].2017.

[26] DENG J,DONG W,SOCHER R,et al.Imagenet:A Largescale Hierarchical Image Database[C]//2009 IEEE Conference on Computer Vision and Pattern Recognition.Ieee,2009:248-255.

[27] LIN T Y,MAIRE M,BELONGIE S,et al.Microsoft coco:Common Objects in Context[C]//Computer Vision-ECCV 2014:13th European Conference,Zurich,Switzerland,September 6-12,2014,Proceedings,Part V 13.Springer International Publishing,2014:740-755.

[28] WEI Y,PAN X,QIN H,et al.Quantization Mimic:Towards Very Tiny Cnn for Object Detection[C]//Proceedings of the European Conference on Computer Vision (ECCV),2018:267-283.

[29] ZHUANG B,LIU L,TAN M,et al.Training Quantized Neural Networks with a Full-precision Auxiliary Module[C]//Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition,2020:1488-1497.

[30] JACOB B,KLIGYS S,CHEN B,et al.Quantization and Training of Neural Networks for Efficient Integer-arithmetic-only Inference[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,2018:2704-2713.

[31] LI R,WANG Y,LIANG F,et al.Fully Quantized Network for Object Detection[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition,2019:2810-2819.

[32] CHEN P,LIU J,ZHUANG B,et al.Aqd:Towards Accurate Quantized Object Detection[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition,2021:104-113.

[33] BENGIO Y,LÉONARD N,COURVILLE A.Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation[J].2013.