机械应力下无取向电工钢片磁致伸缩特性研究

王 振 张艳丽 龚 园 张殿海 谢德馨

（沈阳工业大学电气工程学院 沈阳 110870）

0 引言

对大容量电机及电力变压器而言，铁心的磁致伸缩效应会使铁心尺寸发生微小形变，引起铁心振动与噪声[1-3]。电机铁心由无取向电工钢片叠制而成，铁心在裁剪、冲压、装配等过程中会受到机械应力的作用，改变电工钢片的磁致伸缩特性，加剧铁心的振动[4-5]。为了掌握外加应力对电工钢片磁致伸缩特性的影响，有必要采用先进的实验测量技术测量并分析电工钢片在外加应力下磁致伸缩特性的变化规律，为计算电机铁心形变提供可靠的特性数据，为进一步降低电机铁心振动噪声研究提供有效的措施。

近几年，国外学者对电工钢片磁致伸缩特性的应力敏感性开展了实验测量与特性模拟研究。2007年，英国学者P.I.Anderson 等测量并分析了电工钢片涂层对样片磁致伸缩特性的影响[6]。2012 年，P.K.Klimczyk 等研究了切割方式对取向电工钢片磁致伸缩的影响并测量了三相变压器铁心叠片的局部静态应力[7]。2012 年，日本学者M.Enokizono 等利用六轴应变片测量并分析了外加应力下无取向电工钢片的旋转磁致伸缩特性[8-9]。2014 年，Y.Kai 等测量了双轴应力下无取向电工钢片的矢量磁致伸缩特性[10-11]。2017 年，P.Rasilo 等研究了考虑应力影响的磁滞模型[12]。

国内方面，2013 年，杨庆新教授等在考虑电工钢片受应力影响的情况下，提出了电磁-机械振动耦合数值模型，仿真计算了三相电力变压器铁心的磁致伸缩力[13]。2016 年，唐任远教授等从磁致伸缩引起电机振动的原理出发，基于压磁方程建立了磁致伸缩引起的非金合金定子铁心振动解析模型[14]。2021 年，贲彤等研究人员为了实现硅钢铁心应力加载问题的准确预测，建立了基于应力下饱和磁畴壁移效应的电工钢片磁致伸缩模型[15]。同年，李劲松等研究人员研究了叠置电工钢片结构磁致伸缩变形与机械共振之间的相互作用[16]；钟思翀等学者开展了不同谐波下变压器铁心硅钢片磁化特性与磁致伸缩特性的测量并采用有源降噪分析方法，研究降噪后电力变压器周围声场分布与频率特性[17]；李慧奇等学者分析了不同情况的间谐波激励对变压器励磁电流、磁通以及铁心振动的影响规律[18]。2023 年，袁发庭等结合拉丁超立方抽样实验方法与Kriging模型建立能够准确预测铁心振动位移的优化模型，并获得电抗器铁心的最佳结构[19]。受实验测试发展水平限制，国内对外加应力下电工钢片磁致伸缩特性的实验研究及特性把握还处于起步阶段。

本文基于自主研发的应力下单片电工钢片磁致伸缩应变测量系统，实验研究了外加应力对电工钢片磁致伸缩特性的影响，分析了磁致伸缩随外加应力的变化规律。对退火前后不同切割方式下电工钢片磁致伸缩特性进行了测量，分析了不同切割方式在电工钢片中产生的残余应力。在此基础上，对一台永磁电机定子铁心的磁致伸缩现象进行了仿真计算，分析了外加应力对铁心形变的影响。本文探究了机械应力对电工钢片磁致伸缩的影响，为进一步降低电机铁心振动噪声研究提供了参考。

1 应力下单片电工钢片磁致伸缩特性测量与分析

1.1 测量系统及测量方法

在实验室现有电工钢片磁特性测量装置的基础上，本文开发了如图1a 所示的应力下磁致伸缩测量平台。该测量平台主要由励磁单元、应力单元、磁通密度信号检测单元、磁致伸缩信号检测单元组成。该测量平台所用的励磁装置采用德国Brockhaus 公司生产的单片电工钢片磁特性测量仪，如图1b 所示，图1c 为该励磁装置的实物图。该装置采用闭环控制方式，在30 mm×425 mm 的长方形样片中产生正弦交变的磁通密度信号。同时，该装置还装配有空气压缩机及测压元件，可以实现沿被测样片长度方向施加拉应力或压应力。

图1 应力下电工钢片磁致伸缩特性测量系统Fig.1 Measurement system of magnetostrictive property of electrical steel sheet under stress

在该励磁装置基础上，本文搭建了磁致伸缩信号检测单元。该检测单元由三轴箔式应变计、应变桥盒、应变放大器和BNC 适配器构成，各器件的具体参数见表1。测量前将三轴应变计粘贴于待测样片中心偏上区域，当样片被磁化时会产生微小的几何形变，贴于其上的应变片也会随之产生形变，应变片将形变信号转化为电阻的变化并通过应变桥盒将其转换为电压信号，经应变放大器放大后传给上位机，再转换为相应的应变信号。三轴应变计的三轴栅格用来检测与样片轧制方向分别成0°、45°和 90°的磁致伸缩应变信号。待测样片为50AW600 无取向电工钢片，实验中，磁通密度按正弦周期变化，其峰值Bmax从0.5 T 到1.6 T 变化，步长为0.1 T。

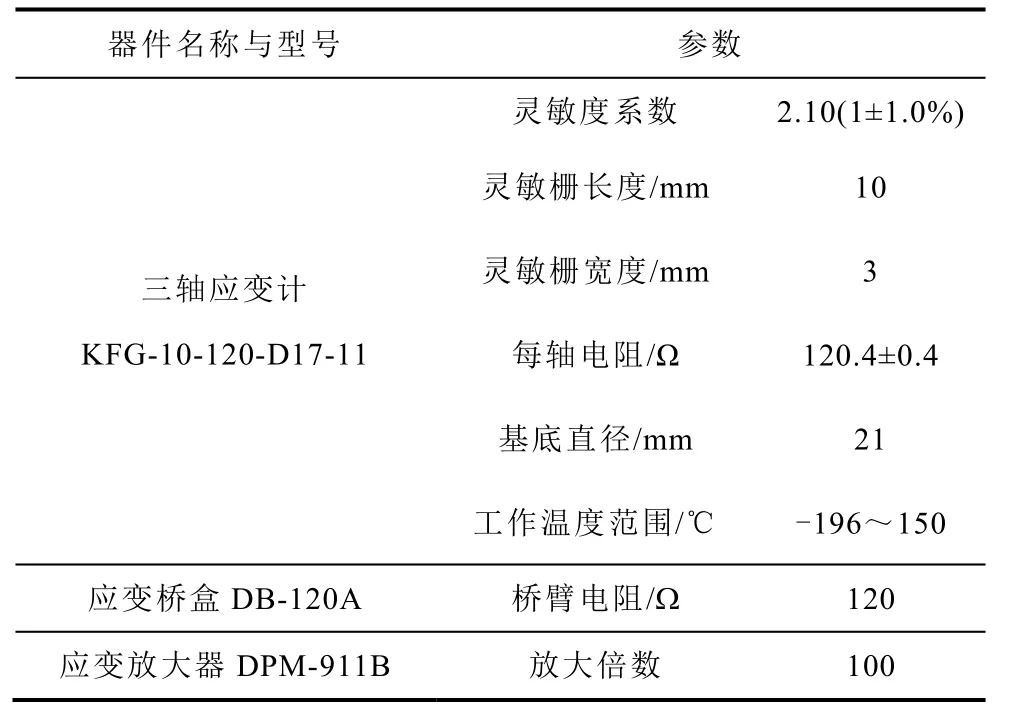
表1 磁致伸缩信号检测单元器件参数Tab.1 Device parameter of magnetostrictive signal detection unit

为了实现沿样片不同方向的磁化，剪裁样片时分别沿着与轧制方向成0°、30°、60°、90°方向进行裁剪。为了研究不同应力下无取向电工钢片的磁致伸缩特性，测量中对样片分别施加0～8 MPa 的压应力或者拉应力，将压应力用“-”表示，拉应力用“+”表示，间隔2 MPa。

依据弹性力学中关于平面应变理论，平面应变中任意一点的应变为[20]

式中，λθ为测量位置任意方向的应变；εx、εy为测量点的线应变；γxy为剪切应变；θ为测量方向与电工钢片轧制方向的夹角。

基于三轴应变计测量得到的三个栅格方向的磁致伸缩应变λa、λb和λc及式（2）可计算两个线应变εx、εy和一个剪切应变γxy。

式中，θa、θb、θc为三轴应变计三个栅格方向与电工钢片轧制方向的夹角。

通过式（3）和式（4）可以分别计算出最大伸长应变λ+(t)（伸长主应变）和最大收缩应变λ-(t)（收缩主应变）及其对应的方向θλ(t)。

1.2 外加应力下的磁致伸缩特性

图2 给出了磁通密度峰值Bmax=1.2 T 沿轧制方向磁化样片时，应变计检测到的与轧制方向分别成0°、45°和90°三个方向的磁致伸缩应变波形。可以看出，无取向电工钢片磁致伸缩在磁化方向（三轴应变计0°轴方向）为伸长应变，在垂直轧制方向为收缩应变，在三轴应变计45°轴方向应变较小。再根据式（2）和式（3）可计算出伸长主应变的波形，如图2b 所示，主应变峰值达到1.72 μm/m。

图2 Bmax=1.2 T、沿轧制方向磁化样片时电工钢片的磁致伸缩应变及对应的伸长主应变Fig.2 Bmax=1.2 T, the magnetostrictive strain of the electrical steel sheet and the corresponding elongation principal strain when the sample is magnetized along the rolling direction

图3 给出了外加应力由-8 MPa 到8 MPa 变化过程中，无取向电工钢片磁致伸缩伸长主应变峰值随磁通密度峰值的变化曲线。可以看出，同一磁通密度下，相比于无外加应力的曲线，外加压力会使磁致伸缩加剧，而外加拉力会使磁致伸缩减小。例如：Bmax=1.3 T，对样片施加-8 MPa 压力时，伸长主应变从无应力下的2.06 μm/m 增至3.37 μm/m，而在 8 MPa 的外加拉力下，伸长主应变减小了0.87 μm/m。从微观机理角度分析，当拉应力和压应力作用在电工钢片上时，机械应力会改变磁畴的结构，从而影响磁化过程，进而对磁致伸缩产生影响。在施加拉应力的情况下，一些磁畴转变为与拉应力方向平行的180°磁畴，180°磁畴仅需通过简单的畴壁移动就可以完成磁化过程，而压应力迫使更多磁畴转变为垂直于外部应力平面的90°磁畴，相比之下， 90°磁畴磁化过程中在畴壁移动的基础上还会产生磁矩旋转，因此90°畴壁运动是磁致伸缩产生的主要原因，所以压应力下的磁致伸缩应变比无应力时更大。当磁通密度较小时，外加应力对磁致伸缩的影响并不明显，磁通密度大于1.0 T 时，应力效应显得尤为显著。此外，同一外加应力下，磁通密度增大会使磁致伸缩逐渐增大。

图3 外加应力下电工钢片伸长主应变曲线Fig.3 Elongation principal strain curve of electrical steel sheet under external stress

图4a 给出了不同磁化方向下电工钢片磁致伸缩伸长主应变曲线。可以看出，不同磁化方向下电工钢片磁致伸缩特性不尽相同。同一磁通密度下，随着磁化方向偏离轧制方向越大，样片的磁致伸缩主应变越大，沿着垂直轧制方向进行磁化，电工钢片的磁致伸缩效应最为明显。这是因为外加磁场沿着横向方向磁化时，更多的90°畴壁会发生运动，位移加大，从而引起更大的磁致伸缩。

图4 有无外加应力下不同磁化方向电工钢片伸长主应变曲线Fig.4 Elongation principal strain curve of electrical steel sheet when different magnetization direction under applied stress

图4b 给出了沿0°、30°、60°、90°磁化样片时（这里称为0°、30°、60°、90°四种样片），在不同应力下的磁致伸缩主应变曲线。其中对0°、30°样片施加-8 MPa 压力，对60°、 90°样片施加8MPa拉力。通过对比图4a 和图4b 中的0°、30°样片曲线，可知外加压力使电工钢片磁致伸缩明显增加，并且Bmax=1.0 T 以上增加明显。例如在Bmax=1.4 T时，由于受-8 MPa 压力的影响，0°样片磁致伸缩主应变由2.14 μm/m 增加到5.06 μm/m，30°样片磁致伸缩主应变由3.49 μm/m 增加到4.93 μm/m。对比图4a 和图4b 中的60°、90°样片曲线可知，外加拉力使电工钢片磁致伸缩减小。

2 不同切割方式对磁致伸缩特性的影响

电机定子铁心在加工过程中，首先需要经过裁剪，不同的裁剪方式会在定子冲片中产生不同的残余应力。本文采用三种方式切割样片，分别是激光切割（Laser）、线切割（W-C）和液压剪板机切割（HPS）。激光切割是将从激光器发射出的激光，经光路系统，聚焦成高功率密度的激光束。激光束照射到工件表面，使工件达到熔点或沸点，同时与光束同轴的高压气体将熔化或气化金属吹走。随着光束与工件相对位置的移动，最终使材料形成切缝，从而达到切割的目的。线切割主要是利用脉冲火花放电对工件进行腐蚀，切割成预期的样式。液压剪板机切割是利用运动的上刀片以及固定的下刀片进行剪切，两刀片之间采用合理的间隙，通过刀片对各种金属板材施加剪切力，就会使板材按所需要的尺寸断裂，达到切割的效果。

图5 给出了Bmax=1.1 T 时样片在三种切割方式下沿轧制方向的磁致伸缩回环，也称蝴蝶曲线。实线（蓝色）代表激光切割（Laser）的样片，长虚线（绿色）代表液压剪板机切割（HPS）的样片，短虚线（红色）代表线切割（W-C）的样片。可以看出，同一批次无取向电工钢片，激光切割的样片在相同情况下产生的磁致伸缩峰值明显大于液压剪板机与线切割方式的磁致伸缩峰值，其应变峰值大约是液压剪板机和线切割方式的2 倍。对比图5a 和图5b可以看出，三种切割方式的样片在压应力的作用下，磁致伸缩峰值均变大，激光切割下的峰值从 3.1 μm/m 增至4.3 μm/m，而液压剪板机切割和线切割的磁致伸缩峰值分别增加了1.5 μm/m 和1.1 μm/m。

图5 三种切割方式下轧制方向磁致伸缩回环Fig.5 Magnetostrictive loops in three cutting ways along the rolling direction

3 退火工艺对磁致伸缩特性的影响

为了进一步研究三种切割方式在样片中留下的残余应力，本文测量了不同切割方式下，退火前后电工钢片磁致伸缩峰峰值随应力的变化曲线，如图6 所示。磁致伸缩峰峰值λpp指一个周期内磁致伸缩波形的波峰与波谷之差，很好地反映了材料发生形变的最大幅度。实验测量中，退火条件为：退火温度660℃，保温时间2 h，升温速度150℃/h。

图6 退火前后电工钢片磁致伸缩峰峰值曲线Fig.6 Peak curve of magnetostrictive peak of electrical steel sheet before and after annealing

从图6 中可以看出，退火后电工钢片的磁致伸缩峰峰值小于退火前，退火处理不但可以提高钢的纯净度，改变晶粒的大小，对改善电工钢片的磁致伸缩特性也起着重要作用。此外，通过退火前后磁致伸缩峰峰值与应力的关系曲线，可以间接分析出加工方式残余在被测样片中的应力。具体方法是通过对比退火前后的磁致伸缩峰峰值曲线，找到同一磁致伸缩峰峰值下最大的应力差值，即可认为是退火处理消除的残余应力。

由图6 可知，线切割产生的残余应力为2.56 MPa，液压剪板机产生的残余应力为2.16 MPa，激光切割产生的残余应力数值最大，高达9.16 MPa。可见，尽管激光切割具有较高的切割精度，但由于激光切割时产生高温将样片边缘融化，然后迅速冷却达到切割效果，这一过程使得磁畴结构发生变化，产生较大残余应力。因此，不同的切割方式虽然可以满足裁剪要求，但是在样片中残留不同大小的残余应力，使得电工钢片产生不同大小的磁致伸缩。在提高设备性能或减小噪声方面，需对切割方式做出选择。

4 应力下电机定子铁心磁致伸缩形变仿真

为了进一步分析电机定子铁心的磁致伸缩，本文利用上述实验测量得到的应力下电工钢片磁致伸缩特性曲线，对一台永磁电机铁心的磁致伸缩效应进行了仿真计算，对比分析了有、无外加应力下铁心形变情况。

表2 给出了一台550 W 永磁电机模型具体参数。具体仿真过程为：首先，利用COMSOL 软件的磁场仿真模块对电机空载磁场进行仿真，得到每个剖分单元的磁通密度，在有限元仿真过程中，激励采用外加电路输入；然后，分别输入测量得到的无应力下及施加外应力下电工钢片磁致伸缩特性B-λ曲线来描述铁心材料的磁致伸缩特性；最后，为了模拟电机在实际工作中的情况，在铁心底部添加固定约束，利用COMSOL 的固体力学模块计算电机的定子铁心形变。

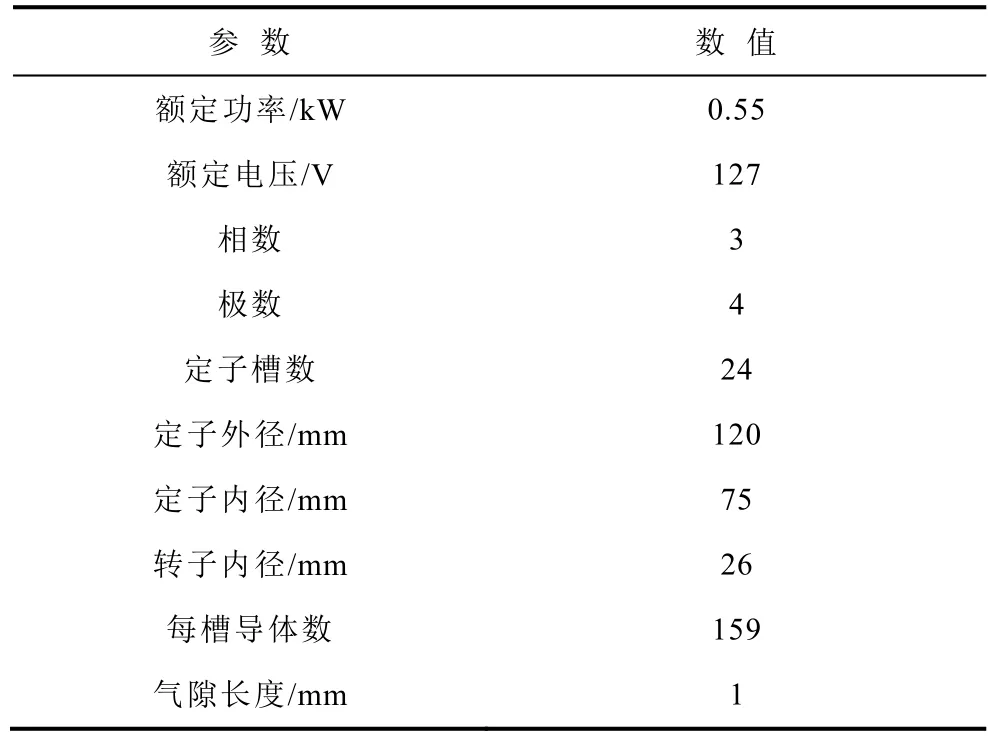
表2 永磁电机模型参数Tab.2 Model parameter of permanent magnet motor

图7 给出了永磁电机磁通密度云图仿真结果。图8 对比给出了有、无应力下永磁电机定子铁心的总位移。对比磁通密度云图可知，磁通密度较大的地方，形变较为严重，由于底部施加了固定约束，使得电机底部的形变微弱。在图8a 中，仿真计算时定子铁心的磁致伸缩特性用无外加应力时电工钢片的磁致伸缩数据描述，可以看出，定子铁心位移最大幅值可以达到141.2 μm。图8a 同时给出了定子齿变形的局部放大图，定子齿发生弯曲，伸出原有的轮廓线。图8b 为-10 MPa 下同一台永磁电机总体位移，此时，铁心的磁通密度与磁致伸缩的关系曲线用实验测得-10 MPa 下的磁致伸缩特性数据描述。对比图8a 和图8b 可知，应力作用使得永磁电机定子铁心变形增大，位移最大幅值增大到155.3 μm，而整体的位移趋势与无应力下的相似。可见，磁致伸缩是电机振动不可忽视的因素，装配时对定子铁心的夹紧力会使得磁致伸缩加剧，对电机的振动产生不利影响。

图7 永磁电机磁通密度分布Fig.7 Magnetic flux density distribution of permanent magnet motor

图8 永磁电机铁心总位移Fig.8 Total displacement diagram of iron core in the permanent magnet motor

5 结论

为研究电工钢片的磁致伸缩对应力的敏感特性，本文搭建了应力下磁致伸缩测量平台，测量并分析了磁通密度峰值、磁化方向、外加应力以及不同切割方式对电工钢片磁致伸缩特性的影响。对不同裁剪方式的被测样片进行了退火处理，对比了退火前后不同应力下磁致伸缩峰峰值的变化。利用测量数据对一台永磁电机进行了仿真，得到了该电机在磁致伸缩作用下的形变分布。得到结论如下：

1）外加压应力会使磁致伸缩加剧，其幅值随着压应力的增加而逐渐增大，而外加拉应力会使磁致伸缩减小。当磁化方向靠近垂直轧制方向时，更多的90°畴壁会发生运动，引起更大的磁致伸缩。

2）不同切割方式对磁致伸缩特性的影响不同。激光切割方式引起的电工钢片磁致伸缩应变大于线切割及液压剪板机切割方式。激光切割使得磁畴结构发生变化，产生较大的残余应力。为降低电机振动噪声，需对切割方式做出合理选择。

3）仿真结果表明，铁心夹紧等工艺产生的机械应力会增大电机铁心的变形，加剧电机振动。

研究结果为进一步降低电机铁心振动噪声研究提供了参考依据。后续工作将依据本文实验测试结果建立磁致伸缩特性模拟的理论模型。