ISRSAC 上基于身份的代理环签名方案设计
2023-11-10袁煜淇张艳硕
袁煜淇 刘 宁 张艳硕
北京电子科技学院, 密码科学与技术系,北京市 100070
1 引言
1.1 研究背景及意义
数字签名技术在数据安全和隐私保护中发挥着尤为重要的作用,大部分签名算法是基于公钥密码体制的,其中经典算法RSA 是1977 年由Rivest 等[1]提出的,其安全性依赖于大整数分解困难问题。 但随着量子计算机的出现,其安全性遭受威胁。 不断有学者提出以RSA 为基础的变种算法,以改进其安全性。 2015 年,Arora 等[24]通过添加额外的第三素数到公私钥的构成中以增加参数n 因子分解的复杂性,并提出了一种加快整个网络的数据交换过程中RSA 算法实现的改进形式,但容易受到选择密文攻击。 2016年,Mustafi 等[25]提出利用双变量双射函数的优化方案。 2018 年,Thangavel 等[2]提出了“用于云数据机密性的改进RSA 安全密码系统(ISRSAC)”,同时证明ISRSAC 算法的安全性高于RSA。
同时,随着技术发展衍生出大量新型应用场景,传统数字签名技术所实现的功能无法满足实际应用需求,故学者们不断提出特殊类型的数字签名以适应使用场景,代理环签名正是其中之一。 1996 年,Mambo 等[3]提出代理签名的概念以满足签名权可授权委托的使用需求。 2001年,Rivest 等[4]提出环签名的概念,主要思想是可实现以匿名方式发布可靠信息。 2003 年,Zhang 等[5]提出代理环签名的概念,结合代理签名和环签名的功能,满足了原始签名人签名权的委托代理及身份匿名的隐私保护需求,能够有效解决代理签名者的隐私保护问题。
在上述基于RSA 的改进算法及具备特殊功能的签名方案的研究背景下,讨论研究基于新型算法构造的具有特殊性质的签名方案,对密码技术应用于诸如电子现金、电子投票、匿名通信等对用户身份隐私保护具有较高要求的领域有重要的理论意义和实用价值。
1.2 国内外研究现状
ISRSAC 算法是在公钥密码体制下以传统RSA 算法为基础的改进安全性的新型算法,而数字签名的安全性极大程度依赖于其核心算法的安全性,故基于ISRSAC 构造的数字签名相比于基于传统RSA 算法的签名方案而言,具有更高的 安 全 性。 2015 年,Thangavel 等[6]提 出 了ESRKGS 算法,该算法将RSA 中的大整数分解由两个素数改进为四个素数,增加了破解难度。2018 年,Thangavel 等[7]再次提出了ISRSAC 算法以改进了Lvy 等人指出的缺陷,进一步增强方案的安全性。 2021 年,Yang 等[8]构造了基于ISRSAC 的数字签名方案,在此基础上分别设计了代理签名方案、广播多重签名方案和有序多重签名方案。 2022 年,刘等[9]在Yang 等人的基础上,设计了基于ISRSAC 的按序代理多重签名以及广播代理多重签名方案。 同年,张等[10]基于ISRSAC 算法构造了一个环签名方案,并证明了一系列安全性质。 目前,不断有学者以ISRSAC为基础构造出适用于不同场景的数字签名方案,将该算法的安全性优势与数字签名技术结合,并研究讨论其在各领域上的应用。
代理环签名的概念是Zhang 等[5]人在2003年提出的,将代理签名和环签名两者的功能特性结合,在实现签名权委托代理的同时有效保护了代理签名人的匿名性。 2004 年,Cheng 等[11]首次提出基于身份的代理环签名,简化了公钥证书管理。 2008 年,Schuldt 等[12]人提出了一个基于身份的代理环签名方案。 2009 年,陈等[13]人提出了基于RSA 的代理环签名方案。 2014 年,Asaar[14]给出了基于身份的代理环签名定义及其安全模型,证明了基于RSA 假设的随机预言机模型下身份基代理环签名方案是安全的。2015 年,张等[15]基于双线性对运算和离散对数的困难性问题,提出了基于身份的代理签名。2018 年,赵等[16]提出了基于身份及RSA 的简短代理环签名方法,缩短密钥及签名长度以提高计算效率。 2019 年,Liu 等[17]提出了一种高效的车载代理环签名方案。 2022 年,袁等[18]通过对SM2 算法进行改进,提出了一种高效的门限环签名方案。
1.3 主要工作及组织结构
本文在文献[16]的基础上做出研究,设计并提出了一个ISRSAC 上基于身份的代理环签名方案。 在随机预言模型下,基于ISRSAC 的方法被证明是安全的。 对于本文在ISRSAC 算法基础上提出的基于身份的代理环签名方案设计,首先在方案构造上是基于公钥密码体制,相比于以往基于双线性对来构造身份基代理环签名的方法做出了创新;同时,方案的安全性与构成代理环的成员数量无关,实现了强不可伪造性;此外,引入安全性高于RSA 的ISRSAC 算法,比现有的基于身份的代理环签名安全性更高。 最后,对方案计算代价进行研究分析,并结合其他方案做出对比说明,进一步突出方案的计算实现的效率。
本文主要内容安排如下:第1 节,主要介绍论文研究的背景意义,概述公钥密码体制下的数字签名技术发展现状,并对ISRSAC 算法和代理环签名国内外研究现状进行阐述。 第2 节,围绕设计ISRSAC 及基于身份的代理环签名方案过程中涉及到的密码学知识进行介绍说明。 第3节,本节介绍了方案设计的相关知识和方案设计的具体内容。 第4 节,对方案的正确性及安全性进行进一步分析及对比说明。 第5 节,对本文主要工作和成果进行总结概述。
2 基础知识
本节将引入相关指标说明ISRSAC 算法的安全性高于RSA。 再依次介绍基于ISRSAC 的一般数字签名、环签名以及代理环签名方案。
2.1 ISRSAC 算法的安全性
ISRSAC 是以RSA 为基础的改进算法,通过强化大整数分解的复杂性,并引入随机数,使得时间复杂度这一指标随着算法复杂程度增加而增大。 具体说明如下:
(1) 强化大整数分解难题。 对于大整数N的生成,由RSA 中两个大素数p,q相乘,改进为两个大自然数p-1,q-1 和两个大素数相乘,增加了因式分解的难度。 因而现有的攻击方法通过因式分解求得私钥的时间复杂度指标增大。
(2) 引入随机数增大攻破难度。 ISRSAC 算法中在私钥生成过程中定义了一个新的安全函数α(n), 同时引入了一个随机数r以生成α(n)。 因此,即使攻击者破解得到p,q,但由于r的随机性,也使攻击者无法破解得到私钥d。
由上述两方面可以明确,ISRSAC 在理论上大大提升了算法破解的时间复杂度,使得其安全性远高于传统RSA,该结论也在Yang 等[8]人的文章中得到证明。
2.2 基于ISRSAC 的数字签名方案
该签名算法中,使用ISRSAC 生成公私钥对。 算法流程分为三个阶段:密钥生成算法、签名生成算法、签名验证算法。 具体如下:
(1) 密钥生成算法:
随机选取大素数p,q且p≠q,p,q >3;计算n=p·q·(p-1)·(q-1),m=p·q;随机选取整数r,其中r满足条件p >2r <q,再计算得到;选取公钥e,其中1<e <α(n),gcd(e,α(n))=1;计算私钥d, 其中d·e≡1(bmodα(n))。 综上,确定公钥(e,m) 和私钥(d,n)。
(2) 签名生成算法:
假设明文为M, 哈希函数为H, 哈希值为H(M)。 私钥为(d,n),计算S≡H(M)dbmodm作为H(M) 的签名。
(3) 签名验证算法:
验证消息M上的签名S,使用同一哈希函数计算H(M),用公钥(e,m)验证H(M)≡Sebmodm是否正确。 如果等式正确,则接受签名。
2.3 基于ISRSAC 的环签名方案
2022 年,张等人提出一个基于ISRSAC 的环签名方案,这一方案主要包含三个算法:密钥生成算法、环签名生成算法、环签名验证算法。
(1) 密钥生成算法
与基于ISRSAC 的一般数字签名方案一致,使用ISRSAC 生成公私钥对。
(2) 环签名生成算法

(3) 环签名验证算法

2.4 基于ISRSAC 的代理环签名方案
基于ISRSAC 算法的代理环签名方案分为四个阶段:系统建立、用户密钥生成阶段、签名阶段以及验签阶段。
(1) 系统建立:通过ISRSAC 算法生成公私钥对分别为(e,m),(d,n); 选择两个Hash 函数:H1:{0,1}*→Zm*,H2:{0,1}*→{0,1}a;公开系统参数(m,e,H1,H2),CA将私钥(d,n)作为主密钥。 随机生成一些素数作为H1函数,本方案选择SM3 函数作为H2函数。
(2) 用户密钥生成阶段1) 独立用户密钥生成。
CA根据每个用户的身份生成唯一编号ID:ID=H1(身份信息) 作为每个用户公钥pk,S为用户ID集合: (ID1,ID2,…,IDn) ∈S;CA计算用户私钥sk=(ID)dbmodn并以安全方式发送给用户。 用户收到密钥后通过ID≡(sk)ebmodm进行验证。 上述用户密钥生成过程可由一个CA单独完成,虽然用户信任CA, 但实际应用中由于CA知道每个用户的密钥,具有过大权限则不能对它进行合理约束。
2) 联合用户密钥生成。

(3) 签名阶段


(4) 验签阶段

3 ISRSAC 上基于身份的代理环签名方案
本节设计并提出了一个ISRSAC 上基于身份的简短代理环签名方案,该方案包括6 个算法:密钥生成(Generation)、提取(Extract)、代理委托(Delegation)、验证委托(VerifyDelegation)、签名(Sign)和验证(Verify)。 该方案能够有效缩短密钥和签名长度,提高了计算效率;在实现上不受代理密钥暴露攻击的影响,具有强不可伪造性。
3.1 符号说明
注意:如果算法A是(t,qg,qp,qe,qe,qprs,e)有界的,即算法的运行时间最多为t, 使得最多在时间qg查询预言机G,在时间qp查询随机预言机P,在时间qe查询Extract, 在时间qd查询ProxyDelegation 和在时间qs查询Sign 预言机,可以至少以ε的概率赢得游戏。

符号 含义 说明X 是一个集合x $←X 表示分配给x 的操作x 是从集合X 均匀随机选择的一个元素x1‖x2‖…xn表示一个编码为字符串组成的对象的有效回收 x1,x2,…xn,是对象空字符串|x | 表示x 的比特长度θ ←C(x1,…xn)#表示算法C 输入x1,…输出到θ
3.2 相关知识
(1) ISRSAC 假设

(2) 基于身份的签名[13]
在签名认证的过程中,将主体公钥与之身份信息相关联是十分有意义的,基于此,Shamir[19]提出了一种基于身份的公钥密码体制。
密钥生成算法为:公钥=H(身份信息); 私钥=F(主密钥,公钥)。
该密钥生成与传统公钥密码体制相反,该计算过程无法公开,只限于特定的主体,以实现对计算出的密钥的保密。 在该公钥密码体制中,用户可以使用身份信息等作为公钥,再用公钥生成私钥,此即为基于身份的公钥密码体制。 在Shamir 的基于身份的签名方案中包括4 步算法[20]。
建立:这个算法由TA(可信机构)运行来生成系统参数和主密钥;
用户密钥的生成:这个算法也由TA执行,输入主密钥和一条任意的比特串id∈{0,1}*,输出与id对应的私钥;
签名:一个签名算法。 输入一条消息和签名者的私钥,输出一个签名;
验证:一个签名的验证算法。 输入一个消息、签名对和id,输出True 或False。
(3) 安全模型
Yu[21]等提出对基于身份的代理环签名方法选择身份攻击,存在A1,A2,A3三种类型的潜在敌手。 安全模型中需要满足代理签名者身份的不可伪造性并且对抗适应性选择消息可实现存在性不可伪造。 若方案对2、3 型敌手安全,则对1 型敌手也是安全的。 在挑战者C和敌手A之间开始以下游戏,验证方案对A1、A2、A3敌手的不可伪造性。
C运行算法ParaGen,用安全参数l获得系统参数para和主密钥(mpk,msk),然后发送主密钥给A。A将密钥与各身份IDu对应并运行KeyExtract 算法,C将私钥xu返回给敌手。 敌手A可以基于消息空间描述符ω上原始签名者的身份ID0和身份集ID请求授权,ID是ID0在ω上签名权委托代理的身份集。C运行KeyExtract得到x0并返回σ0:


对于A=A2,E0:ID0* 没有被要求作为一个Extract 查询;E1:(ω*,ID*) 对没有被要求作为身份下的一个ProxyDelegation 查询。 敌手A2定义为:如果没有有界的(t,qg,qe,qd,ε) 敌手A赢得游戏,基于身份的代理环签名(t,qg,qe,qd,ε) 存在不可伪造性抵抗自适应性选择消息(权证)和选择身份攻击。


3.3 方案设计
根据基于ISRSAC 的代理环签名以及基于身份的签名的构造方法,本节设计并提出了ISRSAC 上基于身份的代理环签名方案。 其中,ID0表示每个原始签名人身份,ID和ID~表示委托代理的身份集及每个子集。 假设:委托代理中代理签名者的身份数量为n(n≥2);ID的每个子集ID~大小为z(z≥2)。 ISRSAC 上基于身份的代理环签名方案由6 个算法构成,分别为:密钥生成(Generation),密钥提取(Extract),代理委托 ( ProxyDelegation ), 代 理 验 证(VerifyDelegation),签名(Sign)和验证(Verify),各算法的具体流程如下。
(1) 系统参数及密钥生成(Generation):
输入系统参数l, 输出系统参数Para和系统主密钥(msk,mpk), 即: (Para,(msk,mpk))←ParaGen(l)。
系统参数如下:假设l0,l1,lN∈N, 且P0:{0,1}*→{0,1}l0,P0:{0,1}*→{0,1}l1,G:{0,1}*→Z*N是随机预言机。 设KGisrsac是ISRSAC 密钥对产生器,输出四元组(n,m,e,d),使α(n)>2ln,e的长度大于l0和l1位。 密钥分配中心KGisrsac生成ISRSAC 参数(n,m,e,d)。 发布mpk=(e,m) 作为主密钥,并保持主密钥msk=(d,n) 的秘密。 因此,公共参数是Para=(P0,P1,G) 和mpk。
(2) 密钥提取(Extract):
输入Para,mpk主密钥msk=d和用户身份的IDu;输出身份IDu相应的密钥(密钥分配中心计算xu=G(IDu)dbmodm, 并将安全且经过身份验证的通道上的用户密钥xu发送给身份为IDu的用户),即xu←Extract(Para,mpk,msk,IDu)。
(3) 委托代理(ProxyDelegation):
若身份ID0的原视签名人决定将其签名权委托给具有身份集ID的委托代理,则采用该算法。 输入Para,mpk,ID0,ID的原始签名者的密钥x0,信息空间描述符ω∈{0,1};输出一个授权σ0,即σ0←ProxyDelegation(Para,mpk,ID0,ID,x0)。
系统参数如下:设ω是一个信息空间描述符,具有身份ID0的原始签名者愿意将他的签名权委托给具有身份集ID的代理签名组,授权σ0=(R0,s0)=(r0ebmodm,r0x0c0bmodm),其中r0←Z*N且c0=P0(R0‖ω‖ID)。 然后,原始签名者发布授权σ0(ω,ID)。
(4) 代理验证(VerifyDelegation):
输入Para,ID0,ID,ω,σ0,如果σ0是一个有效的授权,输出为1,否则为0。 即{0,1} ←VerifyDelegation(Para,mpk,ID0,ID,ω,x0)。
系统参数如下:假设原始签名人的身份ID0,代理签名人的身份集ID,信息空间描述符ω和授权σ0,如果关系s0e=R0G(ID0)c0适用,验证者检查,其中c0=P0(R0‖ω‖ID)。 如果结果如上所述,该授权是有效的;否则,该授权无效。
(5) 签名(Sign):



(6) 验证(Verify):
输入Para,ID0,ID,ID~,ω,message,θ,如果θ是一个基于身份的有效代理环签名,输出是1,否则为0,即{0,1} ←Verify(Para,mpk,ID0,ID~,ω,message,θ)。
系统参数如下:鉴于原始签名者的身份ID0和代理签名者的身份集ID及ID~,消息空间描述符ω, 消息message, 代理环签名θ, 验证过程如下:
1) 如果message∈ω检查;否则,停止;
2) 如果ID~⊆ID,检查;否则,停止;
3) 对于0 ≤u≤z-1,计算Ru=re和cu+1=P1(RuG(IDu)cuR0G(ID0)c0‖ID‖ID~‖IDu‖ω‖message)
接受签名当且仅当cz=c0, 其中c0=P0(R0‖ω‖ID)。
4 ISRSAC 上基于身份的代理环签名方案分析
4.1 正确性分析
下面将对上述方案进行正确性分析,方案的正确性可验证如下:

由上述等式可验证方案的正确性。
4.2 安全性分析
下面对方案的安全性进行具体分析,证明该方案中代理签名者身份隐私具有无条件匿名性并在随机预言模型下该方案具有强不可伪造性。在证明过程中,若ISRSAC 上基于身份的代理环签名方案对2、3 型敌手是安全的,那么它对1 型敌手也能确保安全,为了证明所构造的方案具有不可伪造性,需要证明他是不可伪造的敌手A2,A3。
引理4.1[22]
首先介绍安全模型证明过程中运用的分裂引理。
假设A⊂X×Y,使得Pr[(x,y)∈A]≥δ。对任何α < δ, 定义B={(x,y) ⊂X×Y|Pry′∈Y[(x,y) ∈A] ≥δ-a} 和B-=(X×Y)B,有如下声明:
(1) Pr[B] ≥α;
(2) ∀(x,y)∈B,Pry′∈Y[(x,y)∈A]≥δα;
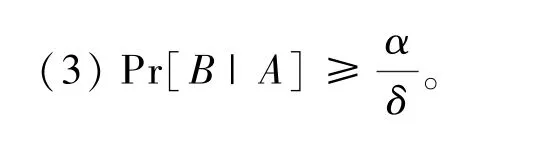
定理4.2

证明:对敌手A2, 构造算法B, 输入(n,m,e,y=γe) 运行A2,输出是算法B运行A2,在输入mpk=(e,m) 和回答A2的预言机查询时,由于A2拥有所有代理签名人的密钥,可以模拟代理环签名,因此预言机访问Sign是没有必要的,消除了方案的不可伪造性。 假设算法CA2保持最初的空关联组T[·] 和TP0[·],并回答如下A2的预言机查询。
(1)P0(R0‖ω‖ID) 查询:

(2)G(IDu) 查询:

(3) 基于IDu的Extract 查询:
算法B 查找T[IDu]=(b,xu,Xu), 如果这项尚未定义,它执行查询G(IDu)。 如果b=0,则B返回xu; 否则,设置badPE←true, 中止A2执行。
(4) 基于身份ID0的(ω,ID) ProxyDelegation查询:

最后,假设如果B不中止签名模拟,在时限t内,至少以概率ε,用原始签名者身份ID0对消息m和授权ω,A2输出一个有效的伪造(R0,s0,c0)。 首先,计算B不中止回答A2的查询的概率下界,需要计算η=Pr[¬badPE]Pr[¬badDG|¬badPE],其中作为A2对Extract 和ProxyDelegation 分别查询的结果,事件badPE和badDG表明B中止签名模拟。 这些概率计算如下:
1) 要求1:
证明:B在A2的Extract 查询中中止的概率为Pr[¬badPE]。 对Extract 查询,当b=1 时,B以概率1-β中止且badPE←true。 故在一个Extract 查询中Pr[¬badPE] 为β,且对于大部分qE的查询,该概率值至少是βqE。
2) 要求2:
证明:事件¬badPE和¬badDG是独立的,故Pr[¬badDG| ¬badPE] = Pr[¬badDG]。 在ProxyDelegation 查 询 中,B中 止 的 概 率 为Pr[¬badDG]。 当查询badDG←true时,B中止,该事件的概率包含两部分,一是以前查询P0发生的ProxyDelegation 模拟中(R0‖ω‖ID) 产生的概率,二是B以前在ProxyDelegation 模拟中使用相同随机性R0的概率。 前者用于qdProxyDelegation 查询的概率至少为qd(qd+qP0)2-lN,后者用于qdProxyDelegation 查询的概率至少为q2d2-lN。 因此,B不中止签名仿真的概率至少是η≥βqE-qd(2qd+qP0)2-lN。 由于伪造是有效的,因此有s0e=R0(G(ID0))c0,在原始签名者身份ID0下,A2没有要求ProxyDelegation 算法授权(ω‖ID),并且ID0没有要求Extract 查询。 另外,G(ID0)=xe0y的概率是1-β。 然后B为ID0查找T[·] 以获取值x0, 并以概率ε1≥ε(1-β)η≥ε(1-β)βqE-qd(2qd+qP0)2-lN返回有用的输出(R0,s0,c0,x0)。 因此,B以概率ε1≥返回可用的输出(R0,s0,c0,x0)。
由于P0是随机预言机,除非在攻击期间被询问,c0=P0(R0‖ω‖ID) 事件发生的概率小于2-l0。 而很可能在成功攻击期间查询(R0‖ω‖ID),对预言机P0查询后生成有效伪造概率的下界是ε2≥ε1- 2-l0。 之后B使用预言机重放技术[23]解决ISRSAC 问题。B算法采用两份A2,猜测固定参数1 ≤p≤(qP0+qd),希望p是查询(R0‖ω‖ID) 到预言机P0的索引,猜测的概率是算法B给出了相同的系统参数,相同的身份和相同的随机比特序列给两份A2,并返回相同的直到查询预言机第p次查询随机应答。 对第p次查询预言机P0,B给Hash 查询Pp两个随机应答c0和c′0,使得c0≠c′0。 因此,在A2从P0查询相同的(R0‖ω‖ID)后,B获得两个有用的输出(R0,s0,c0,x0) 和(R0,s′0,c′0,x0)。 利用引理1 计算B返回一个有用对的概率。


算法B的运行时间t′是A2的2 倍,加上响应Hash 查询所需的时间,qEExtract 和qdProxy-Delegation 查询的时间。 假设ZN中l(多)次模指数运算需要te时间,当所有其他操作需要时间为零,由于每个随机预言机G或Extract 查询需要的时间最多为1 次指数运算,1 个授权模拟需要2 次指数运算,B的运行时间为t′ ≤2(t+(qG+qE+2qd)te),证明完成。
定理4.3

证明:证明对于敌手A3, 构造算法B, 输入((e,m),y=yebmodm) 运行A3,目标是输出γ=bmodm。 算法B运行A3,在输入mpk=(e,m) 和应答A3的预言机查询时,打破该方法的存在不可伪造性。A3拥有原始签名者的私钥,故可以模拟授权,预言机访问ProxyDelegation 是没有必要的。 假设算法B保持初始的空关联数组T[·],TP0[·],TP1[·],并且应答A3的预言机查询如下。
(1)P0(R0‖ω‖ID) 查询:
如果定义TP0[R0‖ω‖ID],则B返回它的值,否则B选择返回TP0[R0‖ω‖ID] 给A3。

(3)G(IDu) 查询:

(4) 基于IDu的Extract 查询:
算法B查找T[IDu]=(b,xu,Xu), 若该项无定义,则执行查询G(IDu)。 当b=0 时,B返回xu;否则,设置badPE←true,中止执行A3。

最终,如果B在签名模拟中没有中止,在时限t内,假定在消息message和空间描述符ω上,基于原始签名者的身份ID0和代理签名者的身份集ID,ID~,A3至少以概率ε输出有效的伪造θ=(R0,r0,…,rz-1,c0)。 得到B不中止应答A3查 询 的 概 率 的 下 界, 需 要 计 算η=Pr[¬badPE]Pr[¬badPS|¬badPE],事件badPE和badPS分别表示因A3的Extract 和Sign 查询,B中止签名模拟。 概率计算如下。
3) 要求3:Pr[¬badPE] ≥βqE
证明:同要求1 中证明。
4) 要求4:
证明:事件¬badPE和¬badPS是独立的,所以Pr[¬badPS| ¬badPE] =Pr[¬badPS]。 在Sign 查询中,Pr[¬badPS] 是B中止的概率。 如果对Sign 查询badPS←true,B中止,并且该事件的概率包括在上一个对预言机P1查询时Sign 模拟中(RuG(IDu)cuR0G(ID0)c0‖ID‖ID~‖IDu‖ω‖message) 产生的概率和在Sign 模拟中B以前使用相同的随机Ru的概率。 对大多数qs,前者的概率最多是qs(qs+qK1)2-lN; 对大多数qprsSign查询,后者的概率最多是

算法B执行另外的随机预言机查询G(IDu)为伪造的身份查找T[IDu]=(b,xu,Xu),并返回(R0,r0,…,rz-1,c0, {xu}0≤u≤z-1,x0,message,ω)。因此,返回一个有用输出的概率至少是ε(1-β)η≥ε(1-β)βqE-qs(2qs+qP1)2-lN。 对于取得最大化值,代替β的


利用引理4.1,将Y分解为(Y′cv),其中Y′是对P1的不同查询所有随机响应的集合,除查询Qv,其应答表示为cv。 引理保证了执行(X,Y) 的子集Ωu,v的存在,例如Pr[Ωu,v |γ′u,v] ≥

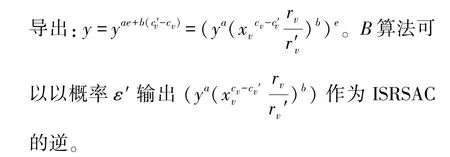
算法B的运行时间t′是A3的两倍,包括t加上响应Hash 查询、qEExtract 查询和qSSign 查询所需的时间。 假设在ZN中,当所有其他操作时间都为零,1 次(多次)指数运算所需时间是te,由于每个随机预言机G 或Extract 查询需要最多1 次指数运算,1 次Sign 模拟需要(2z+1) 指数运算,B的运行时间是t′≤2(t+qG+qE+(2z+1)qs)te,证明完毕。
定理4.4


4.3 对比分析
下面将本文设计代理环签名方案与李等、Asaar 等、赵等、Liu 等、魏等提出的方案分别从所用算法、授权生产和验证代价、代理环签名生成和验证代价以及签名长度这几个方面展开对比分析如下表所示。
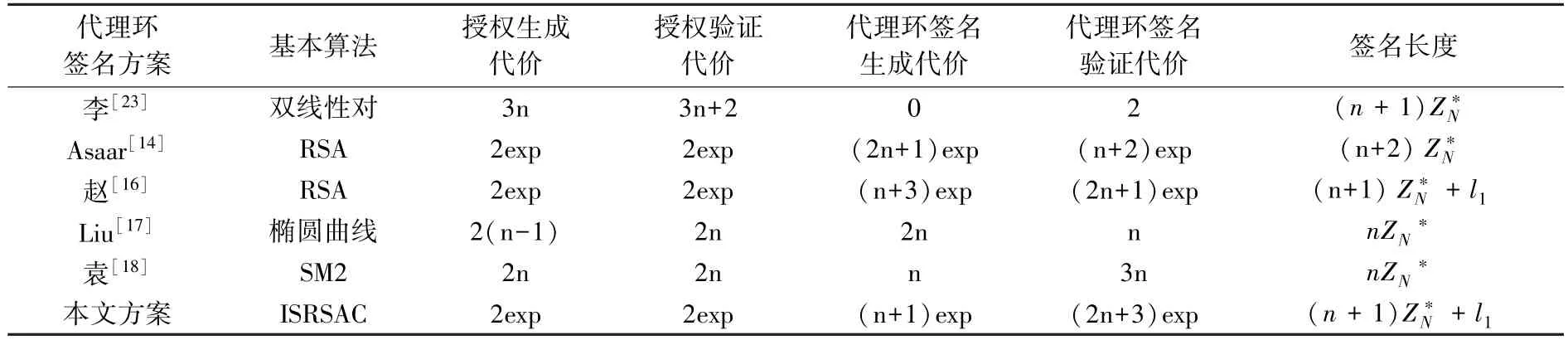
签名方案 基本算法 授权生成代价代理环 授权验证代价代理环签名生成代价代理环签名验证代价 签名长度李[23] 双线性对 3n 3n+2 0 2 (n +1)Z*N Asaar[14] RSA 2exp 2exp (2n+1)exp (n+2)exp (n+2) Z*N赵[16] RSA 2exp 2exp (n+3)exp (2n+1)exp (n+1) Z*N +l1 Liu[17] 椭圆曲线 2(n-1) 2n 2n n nZN*袁[18] SM2 2n 2n n 3n nZN*本文方案 ISRSAC 2exp 2exp (n+1)exp (2n+3)exp (n +1)Z*N +l1
由以上对比分析可看出本文方案的优势在于以下几个方面:一是基于ISRSAC 算法,一方面相比于基于双线性对的方案简化了运算步骤且避免了配对运算,降低了计算复杂度提高了运算效率;另一方面,相比于基于RSA 的方案,以更安全的ISRSAC 算法为基础,在算法层面有效提升了密码体制抵抗攻击时被破解的难度系数,具有更高的安全性、抗攻击性,有广阔的应用前景。 二是基于身份密码体制,对于传统公钥密码体制而言,相比于李等人基于证书的方案,建立并维护公钥证书基础设施往往会带来系统冗杂、成本过高等一系列问题,导致此类签名方案难以在诸如移动自组网等特殊网络环境中应用。 本文方案结合了节点公钥与身份信息,不再需要维护庞大的公钥证书,能够有效降低系统复杂度并显著减少维护代价。 三是计算代价与签名长度,本方案在大幅提升安全性能的同时,相比于同类型基于RSA 的方案,在计算花费代价和签名长度方面并未显著增长,且在“授权”部分,相比于双线性对算法,在“授权”部分的计算代价从O(n) 降低为O(1) 级别,具有更优的运行效率。
5 总结
本文结合赵等人提出的基于身份及RSA 的简短代理环签名方法,引入了安全性更高的ISRSAC 算法,从ISRSAC 假设出发,设计并构造了一个可证明安全的ISRSAC 上基于身份的代理环签名方案,并验证方案正确性,在随机预言机下对方案安全性进行分析说明,结果表明方案具有强不可伪造性,且基于身份和ISRSAC 算法的实现方式,理论上具备更高的安全性,且使安全性与代理环中代理签名者的数量无关。 此外,本方案相比于双线性对的实现方式,避免了配对计算,使运算复杂度降低,提高了运行效率,更易于实现。
综上所述,本文设计的ISRSAC 上基于身份的代理环签名方案,能够有效应用于电子现金、电子投票、电子选举、匿名通信等对用户隐私保护需求更高的领域中,并在日后的诸多电子业务中具有广泛的应用前景。
