S 盒和P 置换安全性指标评估方法的研究与比较*
2023-11-10刘继荣曹宇轩
刘继荣 王 克 曹宇轩
1.北京电子科技学院,北京市 100070
2.浙江省密码技术重点实验室,杭州师范大学,杭州市 311121
1 引言
自第三次科技革命以来,计算机和互联网极大地改变了人类的生活方式,信息传播呈指数爆炸式的增长,同时信息安全问题也日益严峻。 比如,个人数据的泄露会导致不法分子进行电信诈骗;国家机密的泄露会导致社会稳定、经济发展、国家安全受到严重威胁。 在这样的背景下,保护信息安全已然刻不容缓。 密码学是保护数据和通信安全的重要技术,是信息安全的基石[1]。
分组密码是密码学的重要组成部分,具有速度快、易于标准化和便于软件实现等特点,主要应用于数据的加解密处理[2]。 分组密码最常用的两 种 结 构 为: Feistel 结 构 和SP 结 构[3]。Feistel 结构有好的对称性,其重要代表为数据加密标准DES(Data Encryption Standard);SP 结构可看成Feistel 结构的推广,其代表为高级数据加密标准AES(Advanced Encryption Standard)。分组密码的安全性设计原则包含混淆原则和扩散原则两个方面。 特别地,SP 结构中的S 是指混淆层,一般由若干个S 盒并置而成,它们是非线性部件,主要起混淆的作用,同时也是密码算法安全性的重要保障;P 是指P 置换,一般由一个置换或一个可逆变换构成,主要起扩散作用,大多数情况下采用线性变换,也称作P 置换。作为分组算法的核心部件,S 盒和P 置换在算法的设计与分析中扮演重要的角色。
S 盒是分组密码中重要的非线性部件,很大程度上影响着整个密码算法的安全性。 它首次出现在Lucifer 密码[4]中,随后因DES 密码[5]的使用而广为流行。 S 盒是密码算法能够抵抗差分分析和线性分析等攻击的重要保障。 特别地,DES 密码因为S 盒的不平衡性遭到了差分分析和线性分析,AES 密码[6]因为S 盒存在代数表达式项数少的弱点招致代数攻击。 S 盒的密码指标主要有差分均匀度[7]、非线性度[8]、代数次数与代数项数[9]、扩散性[10]、严格雪崩性[11]、代数免疫度[12],主要用来评估抵抗差分分析、线性分析、代数攻击的能力。
P 置换的作用是扩散,是分组密码中重要的线性组件。 P 置换作为迭代型分组密码的一个很重要的部件,它的设计不但影响分组密码算法的安全性,而且影响分组密码在软硬件中的实现效率。 性能良好的P 置换可以有效地抵抗一些著名的密码攻击,如差分分析[13]和线性分析[14]。 P 置换的安全性能主要由分支数[15,16]来衡量,P 置换的分支数越小,分组密码越容易遭受差分分析、线性分析以及一些未知分析方法的攻击。
本文对分组密码算法关键部件S 盒和P 置换进行评估与设计,主要贡献如下:
(1)针对S 盒与P 置换的安全指标,包括S盒的差分均匀度、非线性度、代数次数、代数项数、雪崩特性、扩散特性、代数免疫度、代数项数、不动点个数以及P 置换的矩阵分支数,提出P置换新的指标评估算法,汇总这些安全指标的评估方法,比较各评估方法的优缺点、可用性、实现难度。
(2)基于S 盒和P 置换的安全指标评估方法,选择其中有效的评估方法,对重要分组密码算法中S 盒和P 置换进行评估。 参考AES 算法的设计原理,结合当前流行的超轻量级分组密码算法PRESENT[17],并运用现代分组密码设计中的技巧,筛选出现行标准下效率和安全性最优的S 盒与P 置换的设计方案。
2 预备知识
下面给出关于S 盒和P 置换的相关知识。
2.1 S 盒

其中x=(x1,…,xn)∈Fn2,对每一个1 ≤i≤m,fi∈βn(n元布尔函数全体)称为S 盒的输出函数。
2.2 P 置换
分组密码的P 置换都可以表示为有限域上的线性变换操作,接下来我们需要对线性变换进行具体分析,本节给出分支数的定义。
分支数的概念是由J.Deamen 最先提出的[15,16]。 分支数能够表示在连续两轮的差分或者线性特征中最小的活跃S 盒数量。
定义1[18]:令θ: (F2m)n→ (F2m)nx→θ(x)=y是一个变换,x=(x1,…,xn)∈(F2m)n;则θ的分支数计算方法如公式(1-1)所示:
公式(1-1)中ωb(x) 是非零xi(1 ≤i≤m)的数量,被称作x 的汉明重量。
定义2[18]:线性变换θ的差分分支数计算方法如公式(1-2)所示:
由数学知识可知,任意的线性变换θ一般能够用矩阵M来实现,θt表示θ的转置,于是θt能够用Mt刻画出来。
定义3[18]:线性变换θ的线性分支数计算方法如公式(1-3)所示:
P 置换的扩散性能可以通过分支数来衡量,分支数越大,扩散性能越好。 所以,在构造P 置换时要求分支数尽量达到最大。 当进行差分攻击时,第一步是构造差分路径,在一条差分路径中,如果S 盒的输入存在差分,那么称该S 盒为活跃的,分支数就是最小活跃S 盒的个数。 一个线性变换的差分(线性)分支数越大,那么在进行差分(线性)攻击时要选择的明文数量就越多。 所以说,分支数是构造P 置换的关键性准则之一。
对于任意输入x,肯定满足ωb(θ(x)) ≤n,于是当取汉明重量等于1 的输入时,分支数能够达到的最大值为n+1。 分支数为n+1 时,P 置换的扩散性能是最优的,该P 置换被称为最优P置换。
定义4[15]:将线性分支数和差分分支数同时达到最大值n+1 的变换称作最优扩散变换,其对应的矩阵称作最优扩散矩阵,简称作MDS 矩阵。
3 对S 盒评估方法的比较
分组密码算法的安全性依赖于关键组件的安全性。 因此对分组密码的关键组件进行安全性评估是分组密码算法安全性评估中必不可少的一部分。 本节研究了分组密码的S 盒,P 置换两个关键组件的安全性评估指标,并汇总了当前的一些安全性评估方法,同时对与这些方法进行比对分析。
在关键组件的评估方面,S 盒的安全性很大程度上决定了整个密码算法的安全性,因此我们对S 盒的安全性进行相关性质的评估。
3.1 S 盒的安全性评估
如何全面准确的衡量S 盒的安全性是分组密码研究中的一大难题,目前的研究主要集中在S 盒布尔函数方面的密码特性,这些特性包括正交性、严格雪崩准则(SAC)、差分均匀度、代数次数、代数正规型与代数项数,非线性度和不动点个数等等。 当然,分析S 盒的密码强度,还得结合现有的对分组密码的攻击方法进行分析。 我们查阅、比较了大量国内外关于S 盒研究的论文,得出主流的对S 盒的攻击方法有线性分析、差分分析、代数分析等。 这些攻击方法给我们评价S 盒的安全性提供了一种新思路。 以下给出了国内外论文、研究资料中计算S 盒布尔函数常规指标的方法,我们将对比其中的S 盒线性度计算和差分均匀度计算方法,取其精华,将其思想纳入到S 盒安全性能测试软件的设计之中。
3.1.1 S 盒的非线性度
线性分析是一种高效的主要针对分组密码或者流密码的分析技术。 线性攻击是一种利用明文、密文和子密钥之间高概率发生的线性关系进行攻击的方式。 这是一种已知明文攻击,即攻击者在攻击前可以知道一定量的明文以及对应的密文,但其无法按照意愿去选择明文和相应的密文。
对于线性分析来说,直接影响S 盒抗线性分析能力的指标是线性度与非线性度;从密码学角度来看,希望所选用的布尔函数f(x) 的非线性度越大越好。
定义5[19]:对任意n×m的S 盒S(x),称
为S(x) 的非线性度,称
为S(x) 的线性度。
其中,函数(a) 函数的计算方法如下:
该函数表示的是Sb的线性度。
Lin(S) 这个函数的值越小,表明S 盒抵抗线性分析的能力越强。
关于计算S 盒的线性度的方法有非线性度轮廓测试[20]和Walsh 谱计算[21],这两种方法的比较如表1:

方法 时间复杂度实现难度 优点 缺点[20] 22n+m+1 较难 可靠性高 代码冗长、空间资源消耗大[21] 22n+m+1 简单 轻量化 空间资源消耗最大
方法比较:如表1 所示,对两种非线性度测试算法进行比较。 方法[20]的计算复杂度为22n+m+1次,与方法[21]大致相同;方法[21]的计算逻辑比方法[20]更简单,实现上更容易,考虑到保证软件轻量化的目的,不考虑使用方法[20]来计算S 盒的线性度。 所以我们选择方法[21]作为我们的软件的计算非线性度算法。
3.1.2 S 盒的差分均匀度
差分分析最早出现于20 世纪90 年代。 差分分析的主要思路是考察输入的差分是如何影响对应的输出差分。 通过寻找高概率的差分特征来发现算法的非随机行为,从而进一步地恢复出密钥。 和线性分析类似,差分分析也有衡量标准,差分均匀度。
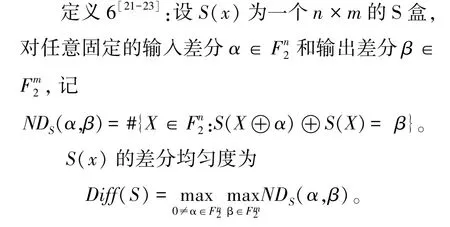
Diff(S)的值与差分对出现的最大概率有关。 一个S 盒的Diff(S)越小,表示这个S 盒的抗差分攻击能力越强。
关于计算S 盒的差分均匀度的方法有快速检测方法[24]和文献[25]中的方法,这两种方法的比较如表2:
方法比较:如表2 所示,对两种差分均匀度测试算法进行比较。 两个方法时间复杂度都是22n,空间复杂度相同,从实现难度分析也相差不大;但方法[25]用在轻量级S 盒上有更好的效率,代码编写难度更小,所以我们选择方法[25]。

方法 时间复杂度实现难度 优点 缺点[24] 22n 较难 原理简单 代码冗长无创新性[25] 22n 简单 轻量化效率更优 大规模S 盒开销大
3.1.3 S 盒的雪崩特性
雪崩效应是指当输入发生最微小的改变时,也会导致输出的不可区分性改变(输出中每个二进制位有50%的概率发生反转)。 对于S 盒的设计者而言,他们推崇S 盒具有较严格的雪崩特性,并将其作为主要研究方向。 有了良好的雪崩效应,分析者或攻击者就很难从输入推测其输出,大大增加了算法的破解难度。
定义7[26]:函数f:GF(28) →GF(2), 若对任意一位输入比特取补,其输出比特有50%的概率取补,则称该函数满足严格雪崩准则SAC(Strict Avalanche Criterion)。 对于严格雪崩准则平均距离的计算,有如下方法:
设多输出布尔函数
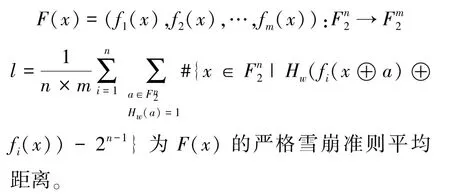
当l=0 时,F(x) 满足严格雪崩准则。 当F(x) 不满足严格雪崩准则时,l越小F(x) 越接近严格雪崩准则。
关于计算S 盒雪崩特性的方法有通过测试它独立矩阵和距离矩阵的办法[27]和[28]中的方法,这两种方法的比较如表3:

方法 时间复杂度实现难度 优点 缺点[27] 22n+m 较难 实现原理简单 代码表示复杂[28] 22n+m 简单 思路清晰、代码易编写 没有效率优化
方法比较:如表3 所示,对两种雪崩特性测试算法进行比较。 两种方法的时间复杂度相差无几,不过方法[27]的代数形式复杂,在代码中表达比较困难;方法[28]思路清晰、实现较简单,所以我们选择方法[28]作为软件计算严格雪崩准则平均距离的方法。
3.1.4 S 盒的代数正规型和项数
布尔函数是研究密码算法和密码技术的重要工具。 S 盒可以看作一个布尔函数,我们在这里给出了几种代数正规型的计算方法。
关于计算S 盒的代数正规型和项数的方法有定义法、利用解方程软件[21]和真值表[21],这三种方法的比较如表4:

方法 空间复杂度实现难度 优点 缺点定义法 22n 中等 代码简短 效率低解方程 22n 简单 效率高轻量化 准确性较低真值表22n 简单 表达形式直观 需要大空间
方法比较:如表4 所示,对三种代数项数测试算法进行比较。 三种方法在计算复杂度上是大体相同的,真值表法更直观但需要开辟较多空间,所以不考虑这种方法。 解方程法和定义法相比,实现起来更容易,代码数量更少,所以我们选择解方程法作为软件计算代数正规型的算法。
3.1.5 S 盒的代数次数
S 盒的代数次数用于衡量S 盒的代数非线性程度,代数次数的大小一定程度上反映了S 盒的线性复杂度,相关研究表明,S 盒的线性复杂度越高,越难用线性表达式逼近,越能够抵抗线性分析。
关于计算S 盒的代数次数方法有定义法、由布尔函数f(x) 的ANF 向量计算代数次数[20]和[21]中的算法,这三种方法的比较如表5:

方法 空间复杂度实现难度 优点 缺点定义法 22n 中等 代码简洁 输入参数多[20] 22n 简单 实现简单代码简洁 测试范围小[21] 2n+1 较难 实现效率高 代码设计难度大
方法比较:如表5 所示,对三种代数次数测试算法进行比较。 定义法的计算复杂度是22n和方法[20]相近,方法[21]的计算复杂度无法确定,但其涉及化简、合并同类项操作,比较适用于手算,软件实现较困难。 方法[20]只需输入ANF 的向量,实现简单,而且ANF 会用于分析S盒布尔函数的其他密码特性,所以我们选择方法[20]作为软件的计算代数次数的算法。
4 对P 置换评估方法的比较
P 置换是分组密码中最为重要的线性组件。对于SP 网络型分组密码和轮函数采用SP 网络的Feistel 网络型分组密码,P 置换的分支数和活跃S 盒的个数有很大关系,分支数越大,活跃S盒的数目也越大。
P 置换的分支数对算法整体抗差分及线性攻击等的强度有重要影响。 一方面,使用分支数较高的线性层可以在较小的轮数内达到较高的抗差分和攻击强度,从而降低算法的整体延迟。另一方面,分支数较高的线性层其实现代价也更大。 因此,设计者往往会进行各种参数的权衡。例如,近些年来,在一些轻量级分组密码算法的设计 中,P 置 换 往 往 不 使 用MDS 矩 阵, 如PRINCE[29]和MIDORI[30]使用的扩散函数分支数为4(最大值为5),而像PRESENT[31]使用的是分支数仅为2 的比特拉线,并通过非线性层和线性层的配合达到更好的扩散效果。
4.1 评估指标
(1)分支数
令θ:(F2m)n→(F2m)nx→θ(x)=y是一个变换,x=(x1,…,xn) ∈(F2m)n;则θ的分支数计算方法如公式(1-1)[6]所示:
(2)P 置换的差分分支数和线性分支数
要想求P 置换的差分分支数和线性分支数,必须要得到P 置换的差分形式和线性形式[6],有以下定理。

其中[z] 表示Z 的向量或矩阵,[z]t表示Z的转置向量或矩阵。

其中,ΔaI,Γai表示输入差分和输入掩码,ΔbI,Γbi表示输出差分和输出掩码。
4.2 评估方法及实现
我们下面进行计算差分分支数的实现,线性分支数的方法类似(不同的是P 为P 置换的转置矩阵或向量),其中方法2 与方法3 是我们所设计的评估算法。
方法1:
算法的基本思想:如果根据定义穷尽输入值的话,数据复杂度太高,比如Camellia 密码,有264个可能的输入,所以为减少计算量,对输入按汉明重量从小到大计算。
分支数测试:
输入:
m:P 置换输入差分ΔX的向量形式(ΔX1,…,ΔXm) 的维数。
n:P 置换输入差分ΔX的向量形式(ΔX1,…,ΔXm) 中ΔXi(1 ≤i≤m) 的比特数。
P:P 置换。
输出:
Pd:差分分支数。
测试过程:
设输入为ΔX=(ΔX1,…,ΔXm) ∈(Fn2)m,将输入值按汉明重量(即非零ΔXi(1 ≤i≤m)的个数)从小到大依次计算其输出值的汉明重量,并求出输入值和输出值的汉明重量之和,如果对汉明重量小于i 的输入计算得到其所有输入值和输出值的汉明重量之和的最小值为n,而这时i >n- 1,则停止搜索,差分分支数即为n。
方法2:
设L 是一个[n,k] -线性码,校验矩阵为H,那么L 的极小距离为d 当且仅当H 中存在d列线性相关,但任意d- 1 列都线性无关。 所以在设计算法时,构造校验矩阵[MI], 设待测的分支数为br,则检验是否任意br- 1 列都线性无关,若是,则检验是否存在br 列线性相关。 在检验时,使用高斯消去法变换矩阵,通过计算秩判断是否线性相关。
分支数测试
输入:
m:P 置换输入差分ΔX的向量形式(ΔX1,…,ΔXm) 的维数。
n:P 置换输入差分ΔX的向量形式(ΔX1,…,ΔXm) 的矩阵。
输出:
Pd:差分分支数。
测试过程:
如算法一所示,该程序是修改后的测试多元域上的dim 维矩阵分支数的程序,使用的是有关分支数和线性码方面的知识,并且使用高斯消去法计算矩阵的线性相关性。

算法一.二元域矩阵分支数的确定1:function BBN(M,dimension)2: InuM←inverse matrix of M 3: miniweight←2·dimension 4: while wb(x) <miniweight/2 do 5: weight←wb(x) +wb(M·x)6: if weight≤miniweight then 7: miniweight←weight 8: end if 9: weight←wb(x) +wb(InvM·x)10: if weight≤miniweight then 11: updata x in the increasing order by Hamming weight 12: return miniweight 13: end function
方法3:利用公式B(θ)=minx≠0(ωb(x)+ωb(θ(x))), 这里,ωb(x) 就是非零元素的个数,即X 的汉明重量。θ(x) 就是P 置换的输出差分。 通过测试X 的汉明重量和线性变换的系数矩阵来确定分支数的大小。
分支数测试
输入:
m:P 置换输入差分ΔX的向量形式(ΔX1,…,ΔXm) 的维数。
n:P 置换输入差分ΔX的向量形式(ΔX1,…,ΔXm) 的矩阵。
输出:
Pd:差分分支数。
测试过程:
设计算法主要是逆推法。 首先定义最小距离为2n,通过验证m个列向量是否线性相关,在此基础上不断把最小距离进行缩小。 而判断是否线性相关,因为是在二元域所以通过异或运算结果是否为0 进行判断。 若是,则将定义的最小距离2n替换为m,最大分支数就是m。
如算法二所示,以ARIA 型扩散结构为例计算分支数。

算法二.伽罗瓦域矩阵分支数的确定1: function BBN(n,BinaryMatrix[MAX] [MAX],Branch-Num)2: while a <sum(n) do 3: c←a 4: while I ←n - 1 ≥0 do 5: if c←0 then 6: B←c%2 c←c/ =2 7: compute the weight of the generatrion part 8: if weight<minweight then 9: miniweight ←weight 10: end while 11: return miniweight 12: end function
4.3 评估方法的对比分析
差分分支数的实现有以下三种,方法1[33]、方法2 和方法3,线性分支数也是类似,这三种方法的对比如下表:
方法比较:如表6 所示,对三种P 置换分支数测试算法进行比较。 方法1 是对输入按汉明重量从小到大计算,通过筛选找到分支数,并且需要测试三个量(汉明重量、向量的维数和比特数)。 方法2 是验证列向量是否线性相关,在此基础上不断把最小距离进行缩小,并且需要测试两个量(二元域上矩阵维数、矩阵的元素)。 方法3 使用的是有关分支数和线性码方面的知识,利用高斯消去法计算矩阵的线性相关性,并且需要两个量(多元域上矩阵维数、矩阵的元素)。因此,方法二和方法三在测试范围、进程内存、CPU 占比等方面都表现优异,我们采用算法二和算法三相结合的方式来进行P 置换分支数的测试。
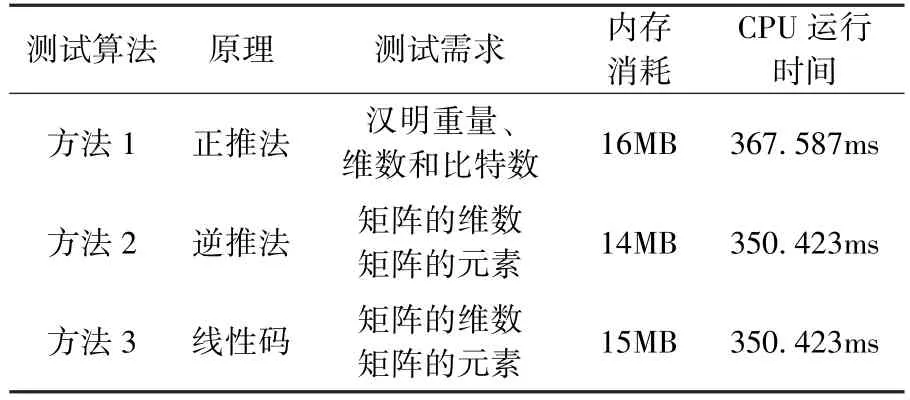
测试算法 原理 测试需求 内存消耗CPU 运行时间方法1 正推法 汉明重量、维数和比特数 16MB 367.587ms方法2 逆推法 矩阵的维数矩阵的元素 14MB 350.423ms方法3 线性码 矩阵的维数矩阵的元素 15MB 350.423ms
5 对S 盒的评估和比较
基于前面S 盒安全指标的评估方法,本节选择其中有效的方法对当下重要的分组密码算法中S 盒进行评估,并在此基础上筛选出现行标准下适于软硬件实现的安全轻量最优S 盒设计方案。
首先我们描述我们采用的评估算法,然后我们针对当下重要的分组密码算法中S 盒进行评估。
5.1 采用的S 盒评估方法
S 盒的代数性质和代数结构很大程度上决定了整个密码算法的安全强度。 关于S 盒的代数性质研究较多,目前最常见的S 盒度量指标列举如下:非线性度、差分均匀性、平衡性、扩散性和可逆性、代数次数及项数分布、正交性、相关免疫性。 对于代数性质较好的S 盒,为了抵抗线性分析,一般都会具有较高的非线性度;为了抵抗差分分析,需要较大的差分均匀性;为了抵抗代数攻击和立方攻击,需要较高的代数次数,并且不同的代数次数的项数分布较均匀。
我们对现有主流分组密码中的S 盒就非线性度、雪崩效应以及扩散特性等性质做了分析与研究。 综合比对多个S 盒设计方案,详细研究这些S 盒的差分均匀度、非线性度、不动点个数、代数次数、代数项数、代数免疫度、雪崩效应以及扩散特性等性质,并与现有的主流分组密码汇总的S 盒各项性能指标进行对比。
5.2 S 盒评估的结果
我们搜集了多种密码算法的S 盒代数表达式、代数性质的比较分析,将AES 算法、SEED 算法、Camellia 算法、SMS4 算法、Blowfish 算法、Serpent 算法和Twofish 算法S 盒的代数性质各项数据指标的计算结果列于下表7 所示。
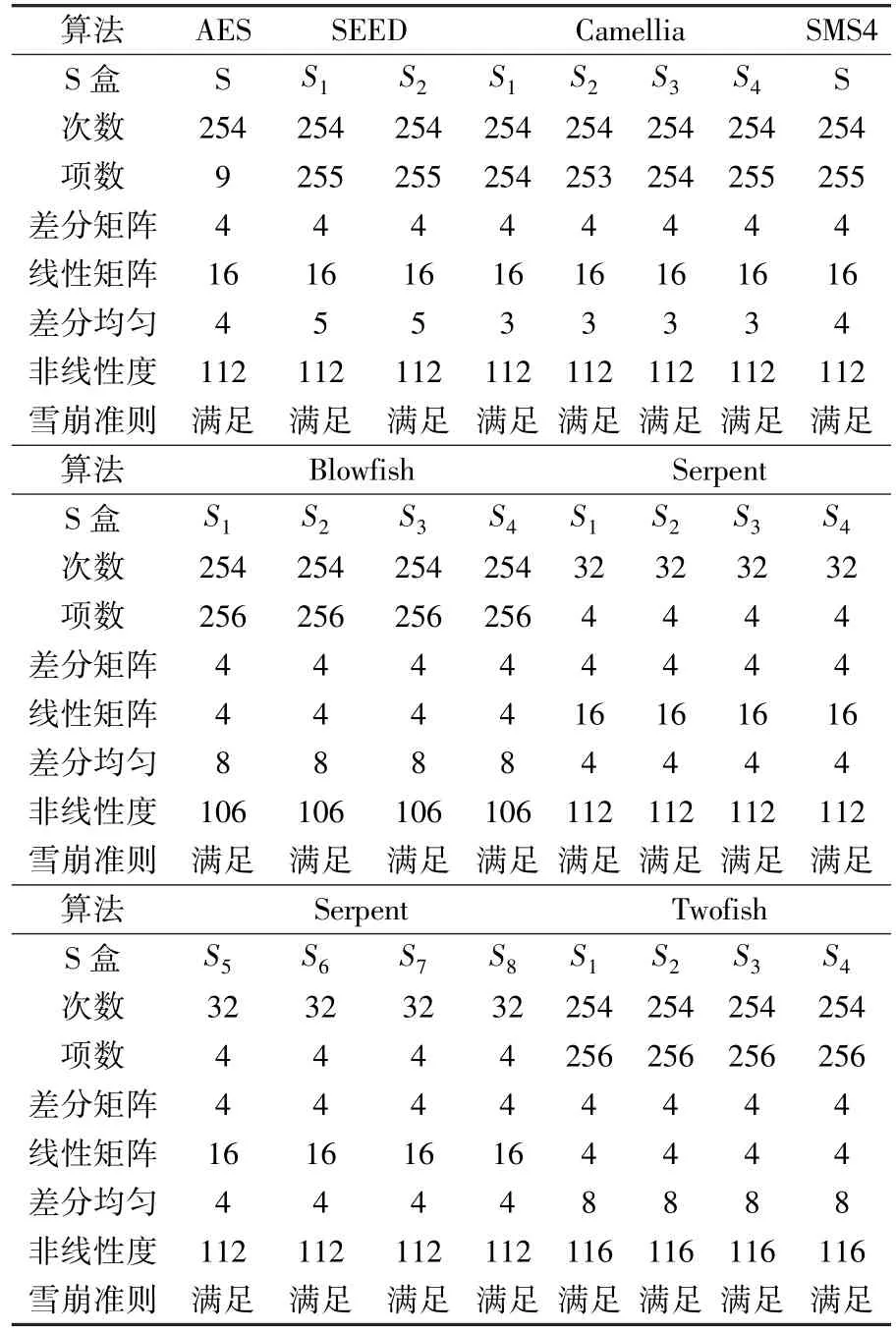
算法 AES SEED Camellia SMS4 S 盒 S S1 S2 S1 S2 S3 S4 S次数 254 254 254 254 254 254 254 254项数 9 255 255 254 253 254 255 255差分矩阵 4 4 4 4 4 4 4 4线性矩阵 16 16 16 16 16 16 16 16差分均匀 4 5 5 3 3 3 3 4非线性度 112 112 112 112 112 112 112 112雪崩准则 满足 满足 满足 满足 满足 满足 满足 满足算法 Blowfish Serpent S 盒 S1 S2 S3 S4 S1 S2 S3 S4次数 254 254 254 254 32 32 32 32项数 256 256 256 256 4 4 4 4差分矩阵 4 4 4 4 4 4 4 4线性矩阵 4 4 4 4 16 16 16 16差分均匀 8 8 8 8 4 4 4 4非线性度 106 106 106 106 112 112 112 112雪崩准则 满足 满足 满足 满足 满足 满足 满足 满足算法 Serpent Twofish S 盒 S5 S6 S7 S8 S1 S2 S3 S4次数 32 32 32 32 254 254 254 254项数 4 4 4 4 256 256 256 256差分矩阵 4 4 4 4 4 4 4 4线性矩阵 16 16 16 16 4 4 4 4差分均匀 4 4 4 4 8 8 8 8非线性度 112 112 112 112 116 116 116 116雪崩准则 满足 满足 满足 满足 满足 满足 满足 满足
7 种算法S 盒的差分矩阵的最大值均为4,且最大值在每一行每一列(首行首列除外)中出现且仅出现1 次。 因此,可以初步认为AES 算法、 SEED 算 法、 Camellia 算 法、 SMS4 算 法、Blowfish 算法、Serpent 算法和Twofish 算法S 盒的差分特性是相当的。 此外,其中5 种算法S 盒的线性矩阵中最大绝对值均为16,且最大值在每一行每一列(首行首列除外)中出现且仅出现5 次。 剩余2 种算法S 盒的线性矩阵中最大绝对值均为4,且最大值在每一行每一列(首行首列除外)中出现且仅出现1 次。 通过上述分析比较,7 种算法在抵抗差分分析的能力是相当的,但抵抗线性分析的能力上AES 算法、SEED算法、Camellia 算法、SMS4 算法和Serpent 算法要优于Blowfish 算法和Twofish 算法。
5.3 对S 盒设计方法的比较
在资源受限的环境中,4-bit S 盒则更受青睐。 因此,本文的目标是从已有的S 盒设计方案中筛选出能抵抗传统密码分析最优的4-bit S盒。 对于4×4 的S 盒,如果它是满足置换性质,并且它的非线性度和差分均匀度都等于4,则这个S 盒是密码学性质最优的S 盒。 本节借助前文第3 节的评估方法,最终得出文献[34]轻量级S 盒的设计方案安全性和效率是相对最优。

代数次数差分均匀度非线性度是否最优最低深度S 盒个数 来源3 4 4 是 2 32 文献[34]3 6 4 否 3 24 文献[35]3 4 6否38Serpent 3 4 8否316PRESENT
如表8 的对比结果可知,同样在文献[35]中作为轻量级算法的S 盒,虽然在非线性度与文献[34]的S 盒持平,但差分均匀度度却没有达到密码学性质最优。 除此之外,文献[34]的设计方案还可以快速地生成更多的最优S 盒,并且设计的S 盒组合逻辑电路最低深度为2,在实现效率方面是优于文献[35]的S 盒。 除此之外,对比Serpent 算法、PRESENT 算法这些经典算法,他们的迭代循环周期没有达到最大,甚至还存在不动点,差分均匀度、扩散特性也还可以做得更好,因此我们选取的设计方案在轻量级密码学性质以及S 盒数量等方面都有明显的优势。当然,文献[34]S 盒的设计方案将在下面进行简要介绍。
本节所选取的文献[34]设计方案是通过三次布尔函数中的变量进行循环移位来构造S 盒。 给定一个布尔函数f,其对应的4×4 的S 盒如下所示。
另外就S 盒的设计我们给出一个定义和一个定理。

设f是一个三次的布尔函数,限定函数所含三次项、二次项的个数。 观察f的函数表达式可知,表达式中有1 个三次项,6 个二次项和4 个一次项,有10(a1~a10)个系数,4 个变量(x,y,z,w)。 从1024 个f中搜索平衡的三次布尔函数,通过编程实现,能找到400 个平衡的f。 所谓平衡是指在16 个变量(0000,0001…,1110,1111)中有8 个变量的函数值为1,8 个变量的函数值为0。 从搜索出来的平衡的三次布尔函数中任取一个,对其变量进行左移1 位、左移2 位、左移3 位,得到函数f1、f2、f3。
将f、f1、f2、f3进行组合即(f、f1、f2、f3),然后对x、y、z、w进行0000 到1111 遍历,计算出此时的f、f1、f2、f3的值,找到置换即(x、y、z、w) →(f、f1、f2、f3)。 此时的置换刚好满足定义1 和定理1,就是所构建的S 盒。 该方法能够找到这样置换的个数是64。
将该设计方案所构造的64 个S 盒的差分分布表分别计算出来,并统计它们的差分均匀度,统计结果如表9 所示,可知该方法所构造的64个S 盒中差分均匀度为4 的有32 个,剩下的S盒均是差分均匀度为6。 由此看来,利用该方法构造的S 盒有一半达到了密码性质最优时的差分均匀度的要求。

代数次数 差分均匀度 非线性度 线性度 S 盒 是否最优 是否平衡 个数3 4 4 8 S3、S4、S7、S8、S11、S12、S15、S16、S19、S20、S23、S24、S27、S28、S31、S32、S35、S36、S39、S40、S43、S44、S47、S48、S51、S52、S55、S56、S59、S60、S63、S64是是 32 212 无 否 否0 3 6 3 4 4 8 S1、S2、S9、S10、S13、S14、S29、S30、S41、S42、S53、S54、S57、S58、S61、S62否否 16 3 6 2 12 S5、S6、S17、S18、S21、S22、S25、S26、S33、S34、S37、S38、S45、S46、S49、S50否否16
在上述构造的64 个S 盒中,有32 个S 盒的非线性度和差分均匀度都等于4,这些S 盒的密码性质最优。 因此,利用文献[34]设计方案构造的64 个S 盒中有一半的S 盒密码性质最优,这些S 盒是安全可用的。 另外该方案是利用代数次数为3 的布尔函数来构造S 盒,所以同时兼顾了S 盒高代数次数的要求。
6 对P 置换的评估和比较
列线性相关,但任意d - 1 列都线性无关。 所以在设计算法时,构造校验矩阵[MI], 设待测的分支数为br,则检验是否任意br -1 列都线性无关,若是,则检验是否存在br 列线性相关。 在检验时,使用高斯消去法变换矩阵,先将矩阵A 与单位矩阵I 进行连接形成一个新的增广矩阵,再通过计算秩判断是否线性相关。
基于前面P 置换的评估,本节选择其中有效的方法对当下重要分组密码算法中的P 置换进行评估,并在此基础上筛选出轻量级P 置换的设计方案。
首先我们描述采用算法二和算法三相结合的方式,然后我们针对当下重要的分组密码算法中P 置换进行评估。
6.1 采用的P 置换评估方法
本文使用有关分支数和线性码方面的知识来测试多元域上的矩阵分支数,并且使用高斯消去法计算矩阵的线性相关性,也就是前文4.2 节所提到的P 置换分支数测试算法2。
主要使用的算法原理为:
设L 是一个[n,k] -线性码,校验矩阵为H,那么L 的极小距离为d 当且仅当H 中存在d
6.2 P 置换评估的结果
我们通过搜索二元域上所有的4×4 可逆矩阵,利用分支数的概念从20000 个候选矩阵中进行筛选,搜索出二元有限域上的MDS 矩阵的数量为零,找到了24 个almost-MDS 矩阵,见下表10 所示。
并且通过对almost-MDS 矩阵进行了研究分析,发现almost-MDS 矩阵不仅实现代价小,而且能够提供可证的安全性,见如下表11 所示:
almost-MDS 矩阵能够在安全性和效率之间进行最佳权衡。 almost-MDS 矩阵虽然具有次优分支数,但是它们比MDS 矩阵需要更少的区域,更短的运行时间,与MDS 矩阵相比,它们在软硬件实现方面效率更高,在almost-MDS 矩阵的实现过程中,它们只需要一个简单的异或操作,就可以大大减少软件和硬件资源的消耗。 许多分组密码算法将almost-MDS 矩阵作为P 置换使用, 如 ARIA[38]、 Camellia[39]、 FIDES[40]、Midori[41]、PRIDE[42]、PRINCE[43]等等,表11 列举了采用almost-MDS 矩阵构造P 置换的一些密码算法。

非对称矩阵 对称矩阵■ ■■■11 01 11 10 10 01 11 11 1 1 0 1 0 1 1 1■ ■■■■ ■■■1 1 1 1 0 1 1 0■ ■■■■ ■■■11 01 10 11 10 01 11 11 0 1 1 1 1 1 1 0■ ■■■■ ■■■1 1 1 1 1 0 0 1■ ■■■■ ■■■11 01 11 10 11 11 01 10 0 1 1 1 1 1 0 1■ ■■■■ ■■■0 1 1 0 1 1 1 1■ ■■■■ ■■■11 01 10 11 11 10 01 11 1 1 0 1 1 0 1 1■ ■■■■ ■■■0 1 1 1 1 1 1 0■ ■■■■ ■■■10 11 01 11 11 10 11 01 1 0 1 1 1 1 1 0■ ■■■■ ■■■1 1 0 1 0 1 1 1■ ■■■■ ■■■10 11 01 11 11 11 10 01 1 1 1 0 1 0 1 1■ ■■■■ ■■■1 0 0 1 1 1 1 1■ ■■■■ ■■■11 10 01 11 01 11 10 11 1 1 0 1 1 0 1 1■ ■■■■ ■■■1 0 1 1 1 1 1 0■ ■■■■ ■■■11 11 01 10 01 10 11 11 1 0 0 1 1 1 1 1■ ■■■■ ■■■1 1 1 1 1 0 0 1■ ■■■■ ■■■10 11 11 01 01 11 11 10 1 1 1 0 0 1 1 1■ ■■■■ ■■■1 1 1 0 0 1 1 1■ ■■■■ ■■■10 11 11 01 01 10 11 11 1 0 1 1 1 1 0 1■ ■■■■ ■■■1 1 1 1 0 1 1 0■ ■■■■ ■■■11 10 11 01 0 1 1 1 1 1 0 1■ ■■■■ ■■■11 11 10 01 0 1 1 0 1 1 1 1■ ■■■■ ■■■01 11 11 10 1 0 1 1 1 1 0 1■ ■■■■ ■■■01 11 10 11 1 1 1 0 1 0 1 1■ ■■■
6.3 对P 置换设计方法的比较
近些年随着物联网等普适计算的发展,计算能力有限的微型设备被广泛应用,这对硬件提出了新的要求。 许多传统密码算法效率较低,因此如何构造一个适用于轻量级密码算法的P 置换受到了广泛关注。 因此本节在前文第四节的基础上,给出我们筛选的轻量级P 置换设计方案[44]。
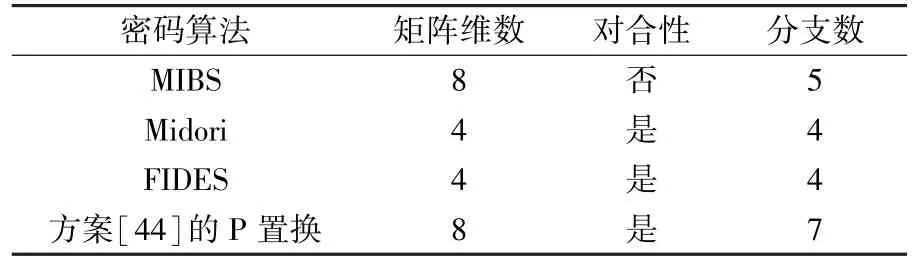
密码算法 矩阵维数 对合性 分支数MIBS 8否5 Midori 4是4 FIDES 4是4方案[44]的P 置换 8 是 7
上述密码算法的P 置换都是作用在F42上,由表12 可以看出,本节选取的设计方案所构造的P 置换分支数要高于MIBS 算法、Midori 算法、FIDES 算法的P 置换,因为考虑到分支数较高的P 置换可以在较小的轮数内达到较高的抗差分和攻击强度,从而降低算法的整体延迟。 因此方案[44]设计构造的P 置换扩散效果相对较优。 除此之外,该方案所构造的对合矩阵可以提供更高级别的扩散,增强密码的安全性,同时处理方式也非常高效,因此它可以在保证安全性的前提下,提高加密效率。 综上,可以得出方案[44]的P 置换在扩散效果和实现效率上都有着明显的优势。 下面对文献[44]S 盒的设计方案进行简要介绍。
该方案设计的P 置换主要是基于密码结构构造P 置换,基于Feistel 结构构造的P 置换逆变换和其本身具有相同的结构,只需简单地按顺序反向使用轮函数即可实现逆变换。 这种结构使P 置换和它的逆变换拥有相同的异或数,特别地,对合的P 置换可以使用相同的代码和电路实现加密和解密,大大节省了软硬件资源,当轮函数是对称的时候,矩阵M 为对合矩阵,如[P1,P2,P1] 和 [P1,P2,P2,P1]。 并 且 由 于Feistel 结构简单,它实际上是利用小矩阵构造大矩阵,如果采用简单的轮函数,将会构造出十分容易实现的P 置换。 为了构造出既安全又高效的P 置换,限定采用三轮Feistel 结构,并且只搜索对合P 置换。 图1 给出了三轮Feistel 结构构造的P 置换,矩阵M =[P1,P2,P3], 逆矩阵为M-1=[P3,P2,P1],
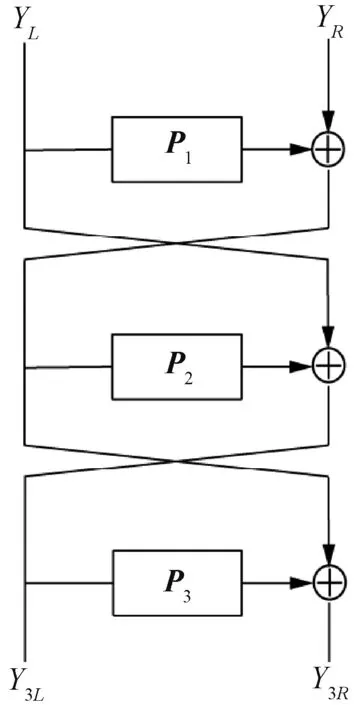
图1 三轮Feistel 结构构造的P 置换
对合P 置换要求轮函数P1和P3相同。 下面给出作用在(Fm2)2n上的基于三轮Feistel 结构构造的轻量级对合P 置换。


因此在(F42)8上构造对合P 置换,当n=4,m=4 时,穷搜了3 项及以下循环移位和异或运算的线性变换作为轮函数的三轮Feistel 的所有可逆P 置换,没有找到MDS 矩阵,得到最好的作用在(F42)8上的对合P 置换分支数为7,共找到1248 个这样的对合P 置换,并且每一个轮函数均为3 项(k=3)。 表13 给出了部分分支数为7 的对合P 置换L(X)。
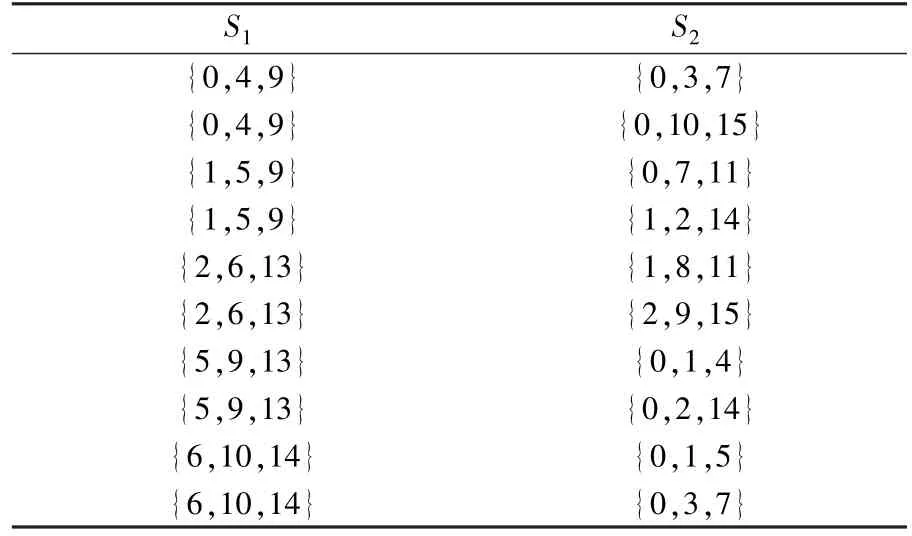
S1 S2{0,4,9} {0,3,7}{0,4,9} {0,10,15}{1,5,9} {0,7,11}{1,5,9} {1,2,14}{2,6,13} {1,8,11}{2,6,13} {2,9,15}{5,9,13} {0,1,4}{5,9,13} {0,2,14}{6,10,14} {0,1,5}{6,10,14} {0,3,7}
综上所述,Feistel 结构因其软硬件实现效率高,加解密一致,加解密速度快等优点受到广大研究者的青睐。 本方案主要是基于三轮Feistel结构构造轻量级P 置换,轮函数采用基于循环移位和异或的线性变换,构造出了一系列作用在(F42)8上分支数为7 的对合P 置换,一方面,对合性质使P 置换的加密和解密操作在硬件上可以使用相同的电路,在软件上可以使用相同的代码,并且轮函数采用基于循环移位和异或运算的线性变换。 不管是移位运算还是循环移位运算,通过软件实现所需的CPU 周期数均很低,大大提高了软件实现效率;另一方面,对于作用在8个4-bit S 盒上的P 置换,分支数为7 的P 置换已经可以提供较好的扩散效果,并且分支数为7的P 置换是安全性和效率方面的权衡。
7 结束语
本文针对分组密码中S 盒和P 置换两个关键组件的评估与比较展开研究,将已有的评估算法在S 盒的代数次数、差分均匀度、非线性度、雪崩特性等方面以及P 置换矩阵分支数进行总结比较。 特别地,本文针对P 置换提出新的评估算法。 在此基础上,我们采用其中有效的评估方法对多种S 盒和P 置换方案进行评估,进而筛选出密码性质最优的S 盒与P 置换设计方案。
S 盒设计方案利用对三次布尔函数中的变量进行循环移位来构造4×4 的S 盒,设计了轻量级分组密码的混淆层。 然后通过求解所构造的S 盒的差分均匀度与非线性度,来衡量它们抵抗差分分析和线性分析的能力。 通过求解可知,32 个S 盒的非线性度与差分均匀度都为4,因此它们是密码性质最优的S 盒,这些S 盒是安全有效的。
P 置换设计方案是基于三轮Feistel 结构构造轻量级P 置换,轮函数采用基于循环移位和异或的线性变换,构造出了一系列作用在(F42)8上分支数为7 的对合P 置换。 在本文综述的4比特最优S 盒以及轻量级P 置换都能够达到一些算法的安全需求,因此二者构造方法都具有可行性和适用性。
