基于随机栅格可视密码与QR 码的双重保护方案

韩妍妍 窦凯丽 魏万奇

北京电子科技学院，北京市 100070

0 引言

随着网络的快速发展，地图等数据量大、内容精度要求较高的图像传输开始由现实物理途径转为网络虚拟途径，实现了由静态、交互到动态传输的演变［1］，但随之而来的是此类图像传输过程中的安全问题。 在提高安全性传输上，学者们提出了一系列加密方式，如对图像进行矢量化混沌加密［2］、基于同态加密添加数字水印［3］或应用可视密码技术一次一密的特点对图像进行加密后传输［4］，但这些加密方式可加密的内容是有限的，对于内容精度要求高的图像来说是无法较好的完成加密与解密，因此需要一种新的方式来满足复杂图像秘密信息量较大、安全需求较高的应用场景，于是本方案在可视密码技术的基础上进行了研究。

可视密码（visual cryptography， VC）是Naor和Adi Shamir［5］于1979 年提出的一种秘密共享方案，由于其仅需人眼视觉系统就可解密的优点而被广泛应用。 之后Blakley［6］提出了（k，n）门限秘密共享方案（secret sharing scheme），即将一幅秘密图像分为n份，只有其中的k份以上叠加才能解密。 但传统的可视密码目前存在着像素扩展度大、需提前设计密码本与基矩阵等问题，因此迫切需要一种新的算法解决此问题，这时随机栅格（random grid， RG）［7］进入了大家的视线。 随机栅格是随机分配黑白二值像素点组合成一幅图像，由于它的随机性，满足了不需提前设计密码本的要求，恰好解决了传统可视密码方案中的问题，为可视密码开拓了新的研究方向。

基于随机栅格的可视密码方案（RG-VCS）是Kafri 和Keren［7］在1987 年首次提出的一种对二进制秘密图像进行加密的方法，他们将二值密钥图像转换成为两个无意义的密码网格，单个网格图像中无法获得任何秘密信息，只有将两个网格图像叠加才可获得其中的秘密信息。 随后Chen 和Tsao［8］在Kafri 和Keren 的基础上提出了（n，n）门限的基于随机栅格的可视密码方案，将只可分解为2 份共享图像的随机栅格可视密码方案扩展为可分解为n份的共享图像，这n份共享图像叠加，即可获得原始秘密内容，实现了参与人数不受限制的功能，但恢复图像的对比度上仍然不佳，于是Yan［9］等人于2018 年开始在提高恢复图像对比度上进行研究，提出利用n位中的随机位弥补视觉质量，虽然此方案对比度有了提升，但其中的k，t，n等值并不是直接给出，因此需要继续进行研究。

随着图像加密的发展，图像逐渐由以往的普通黑白图像变为颜色丰富的彩色图像，从而所含信息量也越来越多［3，4］，导致其应用场景也在逐渐增多，快速响应（quick response，QR）二维码便是其中一个。 QR 码是由日本Denso-Wave 公司在1994 年发明的一种矩阵式二维码，因其识读速度快、存储信息容量大、占用空间小等优点而被广泛应用［10］。 但二维码也存在着一个致命缺点，即公共性太强，任何人扫描后都可获得其所含的内容，因此其无安全加密［11］的特性一直受到各方注意。 为解决QR 码无法传输秘密信息的问题，一些学者提出利用水印技术［12，13］将QR码作为秘密嵌入到掩盖图像中。 在此期间，J Weir［14］等人首次提出将二维码与可视密码相结合，以解决可视密码中身份认证的问题，这为后续可视密码与QR 码相结合的各项研究提供了新思路。 随后Y.Cheng［15］等人提出利用可视化秘密共享方法对二维码进行编码，由于方案中的分享都是有效二维码，因此避免了引起潜在攻击者的怀疑，解密时只有合格的共享份进行异或才能恢复秘密消息。

此前大多数QR 码的研究都是在一级QR码阶段，但随着互联网技术与大数据的快速发展，一级QR 码的储存信息量与安全性无法满足需求，于是国内外学者开始研究更高级别QR码。 Y Cheng［16］等人首先设计了一种具有两级信息存储的QR 码来保护私人消息，对于公共级别信息可以直接扫码得到，而对于私人信息，则需要通过视觉密码方案来进行解密获得。 Z Fu［17］等人对两级信息保护的方案算法继续优化，得到隐私级信息可以通过三种不同的解密方式进行解码，分别适用于相对差1／4 的非计算、相对差1／2 的轻量级计算和相对差1／2 的普通计算环境。 随后，Z Fu［18］等人在两级方案上进一步优化，提出一种基于可视密码的分布式三级QR 码方案，将QR 码分为视觉级、公共级与隐私级QR 码，从而实现更多信息的分级编码。 除改进信息存储方面外，可视密码与QR 码结合应用在其他方面也越来越多，如应用在数字水印［19］等。

所以，依据可视密码与QR 的相关研究，本文针对地图等复杂图像提出一种可视密码与QR 码结合的双重保护方案。 利用QR 码的信息存储量大的优点对地图等复杂图像进行编码保护，再利用随机栅格可视密码的像素扩展低、不需要密码本等优点进行二重加密保护，以实现对秘密图像的加密保护传输。 最后对方案的安全性等性能进行了实验验证和理论证明。

1 基本概念

为方便对于本文后续内容的理解，在表1 中对各类符号做了如下注释。

1.1 随机栅格

随机栅格是一种由Kafri 和Keren［7］在1987年首次提出的对二值图像进行加密的方法，它将一个秘密图像加密成两个随机栅格，单个看是毫无意义的，但其中包含两个栅格信息的区域是相互关联的，当两个栅格叠加在一起，由于透光率的差异，相关区域就会从无意义的图像中被得到，从而可以肉眼直观看到秘密内容。

符号 含义Si 原操作图像QRi 二维码图像Rab 分存图像Rab（i， j） 分存图像（i， j）位置的像素值⊕异或操作L［］ 平均透光率δ对比度ϑ恢复正确率∂像素扩展度

如图1 所示，首先定义一张大小为x×y的图像S，然后以1／2 的概率随机分配黑白二值像素点生成一张同S 相等大小为x×y的分享图像R11，根据图像S 与R11，计算得到另一张分享图像R12。 具体算法为：令S 的像素点为S（i，j），R11的像素点为R11（i，j），R12的像素点为R12（i，j），当S（i，j）＝0 时，R12（i，j）＝R11（i，j）；当S（i，j）＝1 时，R12（i，j）＝1-R11（i，j），以此类推直至计算完整个R12的图像像素点值。 表2 为随机栅格中黑白像素块的生成规则。

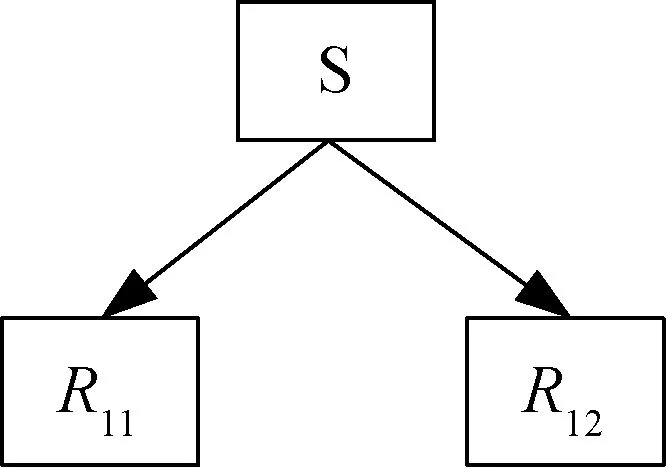
图1 随机栅格加密过程

S 概率 R11 R12秘密恢复（R11 ⊕R12）images/BZ_34_351_2528_417_2594.png1／2images/BZ_34_683_2478_749_2545.pngimages/BZ_34_848_2478_915_2545.pngimages/BZ_34_1047_2478_1114_2545.png1／2images/BZ_34_676_2571_755_2650.pngimages/BZ_34_842_2571_921_2650.pngimages/BZ_34_1047_2578_1114_2644.pngimages/BZ_34_345_2721_423_2799.png1／2images/BZ_34_683_2677_749_2744.pngimages/BZ_34_842_2671_921_2750.pngimages/BZ_34_1041_2671_1120_2750.png1／2images/BZ_34_676_2770_755_2849.pngimages/BZ_34_848_2777_915_2843.pngimages/BZ_34_1041_2770_1120_2849.png

解密时只需叠加两张分享图像R11与R12进行异或运算，即可得到原图像S 的秘密信息。

1.2 QR 码

目前QR 码共有40 种版本，版本1 的规格为21×21 模块数，越高的版本每边依次增加4模块数，直至版本40 的规格为177×177 模块数。 对QR 码来说，其可容纳的资料是多种类型的，如一个版本40 的QR 码可容纳7089 个字节的数字数据、4296 个字节的字母数据、2953 个字节的8 位字节数据及1817 个字节的中国汉字数据等，因此，QR 码可储存的信息量是非常大的。

在构成上，QR 码是由无数的黑白像素块组成，根据其结构可分为功能图形与编码区域两部分，基本结构图如图2 所示。 功能图形包括空白区域、位置探测图形、位置探测图形、定位图形、校正图形等，编码区域包括格式信息、版本信息、数据和纠错码字等。

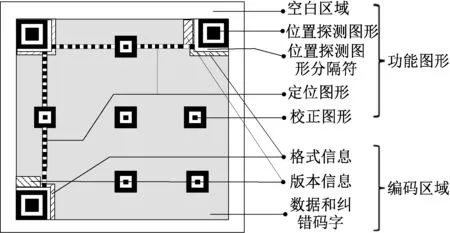
图2 QR 码的基本结构图

其中QR 码的纠错等级共有4 种，如表3 所示，按纠错能力从低到高依次为L、M、Q、H。 纠错能力越高，代表二维码容许出错的概率越高，即某些区域被破坏时仍然可以扫码获得所含内容的概率就越高。

QR 码纠错级别 纠错能力L 7%M 15%Q 25%H 30%

2 方案的设计

本节分为秘密图像双重保护阶段及秘密图像恢复阶段。 秘密图像双重保护阶段中，首先采用QR 码编码的方法将地图等复杂图像编码为QR 码，从而实现第一重的图像保护，其次对QR码进行随机栅格可视密码算法加密，实现第二重的图像保护。 秘密图像双重保护阶段示意图如图3 所示。

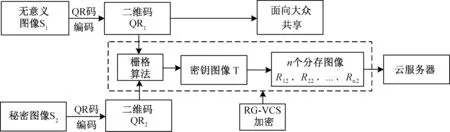
图3 秘密图像双重保护流程图

2.1 秘密图像双重保护阶段

输入：m×n大小的无意义图像S1与m×n大小的秘密图像S2。

输出：1 个二维码QR1面向大众，n个分存图像R12，R22，R32，……，R（n-1）2，R（n-1）1存于云服务器。

步骤1 将S1与S2利用QR 码编码技术编码为两个二维码图像QR1与QR2；

步骤2 对QR1与QR2进行栅格运算得密钥图像T；

步骤3 利用T 采用可视密码算法随机生成R12，R22，R32，……，R（n-1）2，R（n-1）1共n个分存图像存于云服务器中；

步骤4 输出二维码QR1。

2.1.1 图像的QR 码编码

本小节中，对图像编码转换为二维码进行了具体描述，编码流程如图4 所示。 选择一幅无意义内容的图像S1与内容复杂的图像S2进行编码转换为QR 码如下：

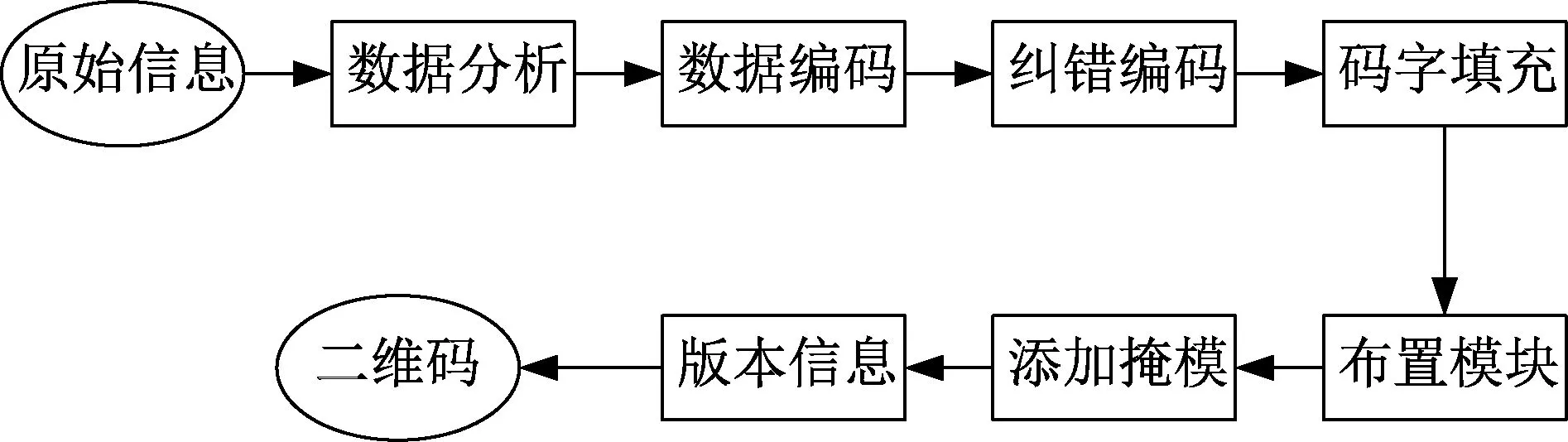
图4 图像的QR 码编码流程

输入：m×n大小的无意义图像S1，m×n大小的图像S2。

输出：二维码QR1与二维码QR2。

步骤1 对需要编码的图像数据进行分析，确定这些数据的字符类型，从而进一步选择满足编码需求QR 码版本信息及纠错等级；

步骤2 按照步骤1 中选择的QR 码版本的编码标准，将数据字符转换成为位流，然后在数据位流的前边添加模式指示符、后边添加终止符，随后将补充完的位流转换为码字，具体转换规则为每8 位成一个码字。 有需要时加入填充字符以保证选择版本的要求数据字数；

步骤3 对数据进行纠错编码，由于QR 码编码采用的是RS 错误控制码（reed-solomon code）来实现其纠错功能的，因此纠错级别及纠错率越高，可以纠正各种符号错误的能力也就越高，最终可被正确解码的概率就越大，本方案选择的纠错率为30%；

步骤4 在版本要求下，将步骤2、3 生成的数据按数据码字、纠错码字的顺序放置形成最终的位流序列。 其中在块序列中所有的数据码字都需放置在第一个纠错码字的前面，随后添加剩余位；

步骤5 将探测图形、分隔符、校正图形和码字，按规则排列后放入二维码矩阵中。 其中每个8 位的码字，需按2 个模块的宽度从二维码矩阵的右下角开始进行一个蛇形排列；位序列的排列，需按由左至右、由最高位到最低位的方向进行排列；

步骤6 在进行编码时，由于编出的码字模样可能会与一些如位置探测图形、分隔符、定位图形等的图形相似，造成识别困难等，因此对符号的编码区域进行掩模处理。 掩模时需用8 种掩模图形依次进行，评价结果后选择最优的一种；

步骤7 将生成版本信息和格式信息进行计算处理后，放入符号的相应位置；

步骤8 输出含无意义图像S1的二维码QR1与图像S2的二维码QR2。

2.1.2 生成密钥图像T

在第一小节的基础上，本小节采用栅格算法将二维码图像QR1与QR2进行运算处理得到密钥图像T，具体步骤如下：

输入：大小为x×y的二维码图像QR1与QR2。

输出：密钥图像T。

步骤1 设i表示行计数器，令i＝1，1 ≤i≤x；

步骤2 设j表示列计数器，令j＝1，1 ≤j≤y；

步骤3 按行列的顺序依次扫描图像QR1与QR2的像素点，即QRχ（i，j），χ＝｛1，2｝；

步骤4 设定阈值k＝127，若QRχ（i，j）≤k，则令QRχ（i，j）＝ 0， 若QRχ（i，j）＞ k， 则 令QRχ（i，j）＝1；

步骤5 通过二值化后的QRχ（i，j），由如下方式产生T（i，j）：

步骤6 重复x×y次步骤5，直至把图像T中的所有像素计算编码完成；

步骤7 输出密钥图像T；

2.1.3 RG-VCS 加密图像

在第二小节的基础上，根据生成的密钥图像T，对其进行RG-VCS 加密，得到n个分存图像R12，R22，R32，……，R（n-1）2，R（n-1）1存于云服务器中。 分存图像的生成流程如图5 所示，具体算法步骤如下：

图5 RG-VCS 的分存份生成图

输入：大小为x×y的密钥图像T。

输 出：n个 分 存 图 像R12，R22，R32，……，R（n-1）2，R（n-1）1。

步骤1 设i表示行计数器，令i＝1，1 ≤i≤x；

步骤2 设j表示列计数器，令j＝1，1 ≤j≤y；

步骤3 设k表示二值图像序号数，令k＝2，2 ≤k≤n- 1；

步骤4 按行列的顺序依次扫描图像T 各（i，j） 位置的像素T（i，j）， 则分存图像R12，R22，R32，……，R（n-1）2分 别 对 应 位 置 （i，j） 的 像 素R12（i，j），R22（i，j），R32（i，j），……，R（n-1）2（i，j） 由步骤5 生成， 分存图像R（n-1）1对应位置（i，j） 的像素R（n-1）1（i，j） 由步骤6～9 生成；

步骤5 生成随机数值｛0，1｝赋值给r12，r22，r32，……，r（n-1）2，经各自随机排列后组合为R12（i，j），R22（i，j），R32（i，j），……，R（n-1）2（i，j）；

步骤6 通过图像T 与随机生成的图像R12得图像R11，生成方式如下：

若图像的像素点值T（i，j）＝0， 则令R11（i，j）＝R12（i，j）；

若图像的像素点值T（i，j）＝1， 则令R11（i，j）＝1-R12（i，j）；

步骤7 通过图像Rk2得图像Rk1，生成方式如下：

当R（k-1）1（i，j）＝0 时，令Rk1（i，j）＝Rk2（i，j）；

当R（k-1）1（i，j）＝ 1 时，令Rk1（i，j）＝1-Rk2（i，j）；

步骤8 令k＝k＋1，若k≤n- 1，则转至步骤7，否则该步骤结束；

步骤9 令R（n-1）1（i，j）＝R（n-2）2（i，j） ⊕R（n-2）1（i，j）；

步骤10 令j＝j＋1，若j≤y，则转至步骤4，否则，令j＝1；

步骤11 令i＝i＋1，若i≤x，则转至步骤4，否则该步骤结束；

步骤12 输出分存图像R12，R22，R32，……，R（n-1）2，R（n-1）1，算法结束。

2.2 秘密图像重建阶段

含密地图等复杂图像经过QR 码编码及RG-VCS 加密后，最终以含有无意义图像内容的二维码图像QR1面向大众，大众扫描QR1后，获得的将是无意义内容的图像S1，有权限人员扫描QR1后获得的是秘密图像S2。 S2的重建过程如图6 所示，具体步骤如下：

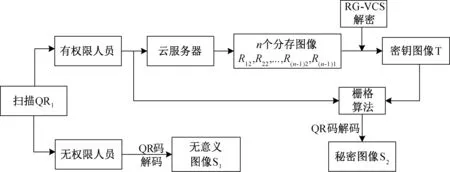
图6 秘密图像重构流程图

输入：二维码图像QR1。

输出：秘密图像S2。

步骤1 手机扫描QR1，进入云服务器；

步骤2 由云服务器中获取分存图像R12，R22，R32，……，R（n-1）2，R（n-1）1；

步骤3 对分存图像R12，R22，R32，……，R（n-1）2，R（n-1）1进行RG-VCS 解密，得密钥图像T。 解密算法如下所示：

（1） 设i表示行计数器，令i＝1，1 ≤i≤x；

（2） 设j表示列计数器，令j＝1，1 ≤j≤y；

（3） 按行列的顺序依次扫描分存图像R12，R22，R32，……，R（n-1）2，R（n-1）1各位置（i，j） 的像素R12（i，j），R22（i，j），R32（i，j），……，R（n-1）2（i，j），R（n-1）1（i，j）；

（4） 令T（i，j）＝R12（i，j）⊕R22（i，j）⊕……⊕R（n-1）2（i，j） ⊕R（n-1）1（i，j）；

（5） 令i＝i＋1，若i≤x，则转至（3），否则，令i＝1；

（6） 令j＝j＋1，若j≤y，则转至（3），否则该步骤结束；

（7） 输出密钥图像T。

步骤4 通过解密得到的密钥图像T 与二维码图像QR1，由以下方式恢复二维码QR2：

（1） 设i表示行计数器，令i＝1，1 ≤i≤x；

（2） 设j表示列计数器，令j＝1，1 ≤j≤y；

（3） 按行列的顺序依次扫描图像T 与QR1各位置（i，j） 的像素T（i，j） 与QR1（i，j）；

（4） 令QR2（i，j）＝T（i，j） ⊕QR1（i，j）；

（5） 重复x×y次（3）～（4），直至把图像QR2中的所有像素计算编码完成；

（6） 输出二维码图像QR2。

步骤5 通过恢复出的二维码QR2获得秘密图像S2，由以下步骤进行QR 码的解码：

（1） 确定版本号。 扫描QR 码读取各信息，如版本信息、纠错等级等，确定QR 码版本号；

（2） 消除掩模。 对编码区域的数据进行异或运算处理，来消除掩模；

（3） 提取字流。 根据模块安排规则提取数据，得数据码字流及纠错码字流；

（4） 纠错。 根据提取到的纠错码字流通过RS 算法进行错误检测，如有，则进行纠错；

（5） 数据解码。

步骤6 输出秘密图像S2。

3 仿真测试及分析

3.1 方案仿真结果

本节中，对提出的双重保护方案进行实验仿真，实验环境为开源库ZXing 及Matlab2021a 版本。 仿真结果如下：

无意义（不含秘密信息）图像S1与含密地图S2如图7 所示，其尺寸均为1024×1024。 由2.1 节的秘密图像分存流程得到的各图像如图8 所示，图8（a）、（b）为二维码图像QR1与QR2，其容错率均为30%，尺寸均为440×440；图8（c）为尺寸440×440 的密钥图像T；图9（d）～（g） 为分存图像R12，R22，……，R（n-1）2，R（n-1）1，其尺寸均为440×440。 经2.2 节的秘密图像恢复流程，得到恢复的图像如图9 所示，图9（a）为恢复的无意义图像，图9（b）为恢复的秘密图像。

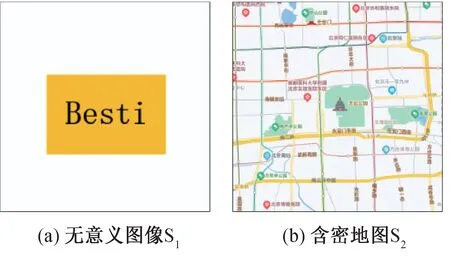
图7 原始图像

图9 方案测试结果

3.2 性能分析

为方便对本方案进行各项分析，首先给出一些相关定义如下：

定义1 平均透光率［20］：对于一幅尺寸为x×y的黑白图像T，令其像素点为T（i，j），则像素点为白的概率为pr［T（i，j）＝1］，像素点为黑的概率为pr［T（i，j）＝0］。 令白像素点的透光度为l［T（i，j）］＝1，黑像素点的透光度为l［T（i，j）］＝0，那么图像T 的平均透光率为：

定义2 图像对比度［20］：令δ为重构图像R｛⊕12，22，…，（n-1）2，（n-1）1｝相对于初始密钥图像T 的对比度为：

其中R｛⊕12，22，…，（n-1）2，（n-1）1｝（i，j）＝R12（i，j） ⊕R22（i，j） ⊕……⊕R（n-1）2（i，j） ⊕R（n-1）1（i，j）；L（R｛⊕12，22，…，（n-1）2，（n-1）1｝［T（0）］） 为相对于初始密钥图像T，恢复图像R｛⊕12，22，…，（n-1）2，（n-1）1｝的黑色区域的透光率；L（R｛⊕12，22，…，（n-1）2，（n-1）1｝［T（1）］）为相对于初始密钥图像 T， 恢复图像R｛⊕12，22，…，（n-1）2，（n-1）1｝的白色区域的透光率。

定义3 恢复正确率： 如果恢复图像R｛⊕12，22，…，（n-1）2，（n-1）1｝和初始密钥图像T 中的对应位置上的像素值相同，则令其值为1，那么恢复正确率ϑ为：

定义4 像素扩展度［20］：像素扩展度指的是初始图像与恢复图像的像素尺寸变化情况。在这里我们定义像素扩展度∂为：

其中｜…｜为图像的大小。

3.2.1 安全性分析

本小节对方案的安全性进行分析，证明方案能够在满足设定的条件下恢复秘密图像信息，窃密者只攻破一层保护方案是无法获得任何秘密图像信息。 为衡量所提方案的安全性，我们采用平均透光率、对比度和恢复正确率进行量化及研究。

定理1 云服务器中需要n个分存份才可恢复出密钥图像中的信息。

定理2 单个二维码图像QR1无法恢复出秘密图像中的信息。

定理3 只有同时获得二维码图像QR1与密钥图像T，才能得到秘密图像中的信息。

3.2.2 鲁棒性分析

为衡量所提方案得出的分享图像鲁棒性，我们采用一些常见的图像攻击手段进行分析。 本小节中，对共享图像二维码QR1依次进行了高斯噪声攻击、旋转攻击、压缩攻击和高斯低通滤波攻击，进行攻击后获得的图像结果均如下图所示，只需扫描攻击后的图像，看是否能正确获得为原图像内容，即可判断本方案所得的共享图像是否含有较强的鲁棒性。

经高斯噪声攻击后的图像如图10 所示，（a）～（d）分别为经过均值为0 方差为0.02、均值为0 方差为0.03、均值为0.02 方差为0.01、均值为0.4 方差为0.4 的参数攻击；经旋转攻击后的图像如图11 所示，（a）～（c）分别为经过旋转角度为20°、80°和150°的参数攻击；经压缩攻击后的图像如图12 所示，压缩参数为4；经高斯低通滤波攻击后的图像如图13 所示，攻击参数为50。

图10 添加高斯噪声攻击

图11 添加旋转攻击

图12 添加压缩攻击

图13 添加高斯低通滤波攻击

由攻击结果可以看到，攻击后的图像虽较为模糊，但没有缺失任何图像信息，肉眼可见其基本的二维码结构都是存在的，而且由于二维码特有的定位图形等结构，经扫描后均可获得其所含内容，这表明本方案得到的分享图像具有较好的鲁棒性。

3.2.3 方案对比

在本小节中，我们选取以往可视密码领域中的优质文章进行对比，对比内容如表4 所示。

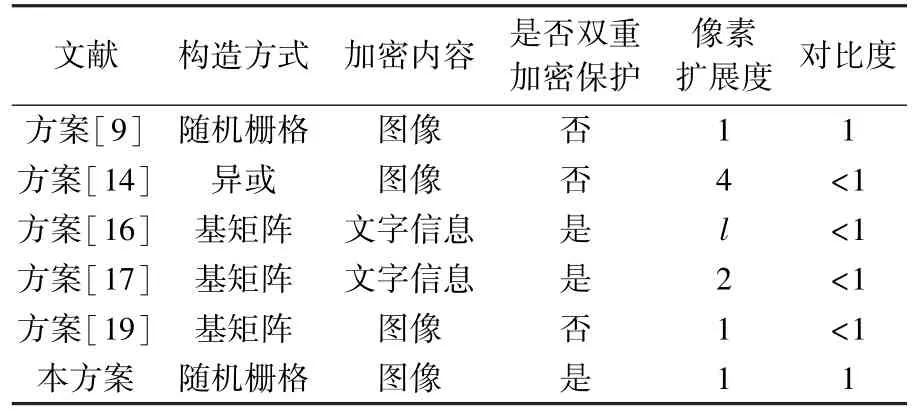
文献 构造方式 加密内容 是否双重加密保护像素扩展度 对比度方案［9］ 随机栅格 图像 否 1 1方案［14］ 异或 图像 否 4 ＜1方案［16］ 基矩阵 文字信息 是 l ＜1方案［17］ 基矩阵 文字信息 是 2 ＜1方案［19］ 基矩阵 图像 否 1 ＜1本方案 随机栅格 图像 是 1 1

由表中内容可以看到，现有的可视密码与QR 码结合的方案中均采取了构造基矩阵的加密方式，而本方案采取的加密方式为随机栅格的基本异或，省去了设计密码本或基矩阵的复杂操作，使得加密过程更加简洁，从而在计算量上要比其他方案小得多。

此外本方案中，由于生成二维码图像QR1与QR2的尺寸均为440×440，经RG-VCS 加密后的各个分存图像尺寸也为440×440，说明分存图像没有像素扩展，那么经恢复叠加后的图像像素扩展度1，说明图像恢复效果较好，由表4 可知，仅有方案9、方案19 与本方案可达到无像素扩展度。同样的，在对比度性能上与其他方案进行比较后可以发现，在可视密码与QR 码相结合的方案中，仅有本方案可以实现图像的完全恢复，因此QR 码解码器可正确识别出秘密图像。

综上对比，本方案不仅可实现秘密图像的完全恢复，且与其他可视密码和QR 码结合的方案相比在像素扩展和计算量上实现了最优。

4 结束语

本文针对地图等复杂图像，提出了一种基于随机栅格可视密码和QR 码的双重保护方案。在此方案中，对含密内容复杂的图像进行加密处理后，只需共享一个QR 码便可实现秘密信息的安全传输，有效地优化了传播过程繁琐的问题。此外，窃密者窃取单个信息后无法解得秘密内容信息，从而实现了秘密信息的双重保护的效果，并起到了大众与解密者的分级管控效果。