基于3种机器学习算法的台风频数预测

荣新，覃卫坚，韦文山

（1.广西民族大学电子信息学院，广西南宁 530000；2.广西气候中心，广西南宁 530022）

0 引言

台风是一种破坏性极大的气象灾害，台风期间常伴随狂风、暴雨、风暴潮等现象。广西位于中国南部沿海地区，每年平均受5 个台风的影响。台风常给广西造成严重的经济损失和人员伤亡，如2001年7 月2—9 日，台风“榴莲”和台风“尤特”给广西带来强降雨，导致左江、右江、邕江、郁江、浔江洪水泛滥，百色市遭遇了百年不遇的洪涝灾害，1 650 万人受灾，24 人死亡，直接经济损失达159 亿元。因此，提高预测影响台风频数的气候要素的能力，对提前做好台风防范工作、减少灾害损失具有重要意义。

台风预报方法研究一直受到人们的关注，传统的线性回归、广义加性模式、动态统计混合模式等统计预报方法在热带气旋活动预测中取得了巨大的成功[1-8]。近年来，基于机器学习和人工智能算法在处理非线性问题上有较好的自适应学习能力，被广泛应用于天气预报中[9-15]，例如：在探索台风生成、路径以及强度时，CHEN 等[16]关注了大气和海洋变量的时空相关性，将台风的形成和强度预报分别定义为时空序列预报的分类和回归问题，建立了卷积神经网络-长短期记忆网络（Convolutional Neural Networks-Long Short-Term Memory，CNN-LSTM）混合预测模型；高珊等[17]、徐光宁[18]分别运用LSTM和深度学习建立台风强度预测模型；HAGHROOSTA等[19]在台风强度预测上证明了运用自适应模糊神经网络（Adaptive-Network-based Fuzzy Inference Systems，ANFIS）方法优于单独的人工神经网络方法；GAO 等[20]建立了基于LSTM 的台风路径预报模型，得到了理想的6～24 h 的台风路径预报结果；SONG 等[21]结合两次数据降维，建立了基于支持向量回归（Support Vector Regression，SVR）方法的台风路径预报；LIU 等[22]通过粒子群投影寻踪和模糊数学计算权重来优化预测因子，建立了基于自然正交展开和组合权值的非线性小波神经网络模型，同样TAN 等[23]使用最小绝对收缩和选择算子方法获取预测因子并结合随机森林（Random Forest，RF）建立了预测方案，两者在热带气旋频数预测上都取得了较好的预测结果。综上可见机器学习和人工智能算法多应用于台风路径、强度等天气预报中，而在台风频数预测的应用中还不多见。本文以影响广西的台风年频数作为研究对象，针对台风频数预测的非线性特点，汲取当前人工智能的研究成果筛选最优的预测因子，在数据处理上运用具有优越选择特征的随机森林方法进行因子二次筛选来得到最优预测因子，使用SVR、RF 以及循环门单元（Gated Recurrent Unit，GRU）3种机器学习算法建立台风个数预测模型，综合对比分析得出最优算法，为年度台风频数预测提供新的可行性方法。

1 资料与方法

1.1 资料来源

影响广西台风观测数据（1951—2020 年）来源于中国气象局上海台风研究所提供的台风年鉴和热带气旋年鉴。台风等级包括台风、热带风暴及热带低压，影响广西的台风定义为进入19°N 以北、112°E以西的台风[24]。

国家气候中心提供了1951—2020 年88 项大气环流特征向量和26 项海温指数资料（获取地址：http://cmdp.ncc-cma.net/Monitoring/cn_index_130.php）。对上述资料进行归一化预处理，归一化公式为：

式中：i表示第i年；k表示第k个特征因子。

1.2 岭回归模型方法

线性回归分析是探索因变量和自变量关系程度的统计方法，通过将真实值与预测值的平方误差最小化，可建立反应变数（Y）和解释变数（X）之间的关系模型。最小二乘法代价函数为：

式中：α是线性回归系数。

解出系数α为：

式中：XTX为满秩矩阵。

为了解决线性回归分析中过拟合的问题，岭回归方法（Ridge Regression，RR）在建模时加入正则化项，在矩阵XTX的对角线元素上加入岭系数σ，代价函数hα（α）转变为：

得到系数α的解：

式中：σ是超参数，可通过调节σ的值来改变对α的惩罚强度。

1.3 SVR模型方法

SVR 模型方法是一种用于分类和回归、有监督的机器学习算法，在处理高维问题方面具有较强的鲁棒性。SVR 的主要思想是利用支持向量机找到可能的最佳预测模型，并容忍一些预测误差[25]。首先需要构建一个样本标签，选择最有影响力的样本集构造超平面，方程表示为：

式中：w表示加权矩阵；b为偏置项。当且仅当训练样本落入划分的超平面外时计算损失，将回归风险最小化为：

式中：B为正则化常数；g(xk)为第k个样本的预测值；yk为第k个真实值；lθ为不敏感损失函数，其中θ为容忍偏差。

本模型引入高斯核函数G(x,xk)，可将样本从原始空间映射到更高维的特征空间以获得更高的预测精度，超平面所对应的模型变为：

1.4 RF模型方法

RF 模型方法是决策树方法的改进[26]。RF 算法由许多决策树组成，把多个决策树的计算结果进行平均作为最后的输出结果。基本流程见图1。对于给定的原始数据D（xk,k∈1,2,3,…,n)：

图1 RF方法流程图Fig.1 RF method flow chart

①首先在原始数据D中有放回的随机抽样，生成m个子元组，保证每个子元组数量等于总数据集数。

②在建立决策树的过程中随机抽取备用特征，把最优特征子集划分为局部训练集，构造m棵决策树，剩余样本形成袋外数据（OOB）用于估计随机森林的拟合度。构造决策树使用基尼指数（Gini）[27]最小化准则进行分裂，Gini值越小，数据集的纯度就越高。Gini指数可表示为：

式中：ak为训练集中样本属于某一类的概率。

③特征选择。

a.计算特征pi在节点j中的基尼指数变化值，公式为：

式中：Gini(j)表示分枝前的基尼指数；Gini(l)和Gini(r)则为节点j分枝后产生的两个新节点的基尼指数。

b.计算特征pi在第z棵决策树上的基尼指数变化量：

式中：N为节点集合。

c.求每个特征对随机森林每棵树的贡献值，即重要程度：

d.对每一个节点求得贡献值后进行比较和排序[28]。

④将m棵树组成随机森林，求平均值并作为最后输出的预测结果。

1.5 GRU模型方法

GRU 模型方法是一种高级的长短期记忆技术[29]，是LSTM 算法的一个变体，GRU简化了LSTM算法的3 层门循环，将单元状态与输出状态合二为一，仅保留了两层的门循环即重置门和更新门。基本流程见图2。

图2 GRU方法基本流程图Fig.2 GRU method flow chart

GRU方法的公式表示为：

式中：zt表示更新门；rt表示重置门；w表示循环层权重；xt为t时刻的输入；It表示t时刻的输出状态。使用GRU 算法可以有效解决数据序列在训练过程中出现的梯度消失和爆炸问题。

2 预测模型及效果检验

2.1 筛选预报因子

2.1.1 初次筛选因子

给定一组数据D={(Xk,Yk)},k∈n，设相关系数为r，r可表示为：

式中：为X的平均值；为Y的平均值。

计算1951—2015年影响广西的台风年频数时间序列与同一年、前一年各月各种大气环流和海温指数的相关系数，初步筛选出相关系数绝对值达到0.4、通过水平为0.01的显著性检验的环流特征量和海温指数作为预报因子，共得到24个预报因子（见表1）。

表1 初选得到的预报因子Tab.1 Predictors obtained from the primary selection

2.1.2 二次筛选因子

通常预报因子之间的多重共线性会导致解释变量之间出现相当大的冗余，为了能够更好地反映预报因子场的综合信息，需要在已选定的一批因子中得到最优因子，进一步提高预测精度，降低计算的复杂度。使用RF方法对上节得到的24个预报因子进行二次筛选，使用经过训练的RF 模型，计算每个因子的重要程度，按照从大到小的顺序逐个输出，筛选出重要性值相对较高的因子。由于前3 位因子的重要性值最高，之后因子的重要性值有较大幅度的减小（如第四位重要性值仅为0.030 33），因此最后得到3 个预报因子（见表2），分别为前一年9月欧亚纬向环流指数、同一年2月NINO 1+2区海表温度距平指数、前一年6 月大西洋经向模式风指数（Atlantic Meridional Mode，AMM），该区域多处于西太平洋台风生成的区域。

表2 二次筛选得到的特征因子Tab.2 Characteristic factors obtained from the secondary screening

2.2 RR模型预报

设台风样本数据为D（xk,k∈1,2,3,…,n），绝对误差计算公式为：

相对误差计算公式为：

基于初次筛选因子和二次筛选因子建立RR 预报模型。利用24个因子建立预报模型，调节岭参数值为0.7 时预测结果最佳，由表3 可知5 a 独立样本的预测平均绝对误差为1.46，平均相对误差为38.13%。利用二次筛选得到的3 个因子建立RR 预报模型，调节岭参数σ为0.6 时，训练64 a 台风样本集效果最佳（见图3），平均绝对误差为2.12；5 a独立样本预测结果见表3，预测平均值为4.31，较使用初次筛选因子的预测更接近实况平均值，平均绝对误差为1.03，平均相对误差为24.02%，较使用24 个因子的RR 模型预测的平均绝对误差减少0.43，平均相对误差减少14.11%，预测效果明显提高。

表3 2016—2020年台风频数RR模型预报结果Tab.3 RR model forecast results of typhoon number in 2016—2020

图3 RR模型训练拟合预报和实况序列Fig.3 RR model training to fit forecasts and observations

2.3 SVR模型预报

SVR 采用liblinear 库来实现，选取参数惩罚函数C=0.1，损失函数explosion=2.0，最大迭代次数默认为10 000 次，训练集为64 a 台风个数。当预报因子为24 个时，5 a 独立样本预测结果见表4，预报误差绝对值平均为0.83，平均相对误差为17.28%。当预报因子为3 个时，预测样本选取5 a 的数据，从训练集的拟合曲线和实况序列来看（见图4），预测值波动幅度较实况小，对极端异常台风个数的预测能力较低，如2004 年无台风影响广西时预测值为4个，2013 年台风达到9 个时预测值也为4 个，相对误差为55.56%，平均绝对误差为1.56，较岭回归减少0.56；5 a 独立样本预测结果见表4，预测平均值为4.08，总体上较实况值偏小，预测平均绝对误差为0.72，平均相对误差为16.55%，较岭回归方法分别减少了0.31 和7.47%，较使用24 个因子预测的平均绝对误差减少0.11，平均相对误差减少0.73%。

表4 2016—2020年台风频数SVR模型预报结果Tab.4 SVR model forecast results of typhoon number in 2016—2020

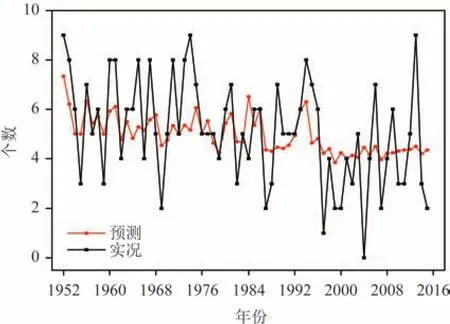
图4 SVR模型训练拟合预报和实况序列Fig.4 SVR model training to fit forecasts and observations

2.4 RF模型预报

使用RF 方法建模预报，设置n_estimators=50，n_jobs=-1，random_state=10。当预测因子为24 个时，5 a 独立样本预测结果见表5，平均绝对误差为0.75，平均相对误差为16.78%。利用二次筛选得到的3个预报因子，5 a独立样本预测值平均为3.65，总体上比实况值略偏小，预测平均绝对误差为0.68，平均相对误差为14.58%，分别比岭回归方法减少了0.35 和9.44%，比初次选取的因子预测平均绝对误差减少0.07，平均相对误差减少2.2%；RF 方法训练的拟合曲线和实况序列见图5，预测值和实况值基本吻合，尤其是对极端年份的预测能力较SVR 模型和RR模型有较大提高，如2013年台风为9个，RF方法预测值为8个，非常接近；拟合预测平均绝对误差为0.64，较岭回归减少1.48。

表5 2016—2020年台风频数RF模型预报结果Tab.5 RF model forecast results of typhoon number in 2016—2020

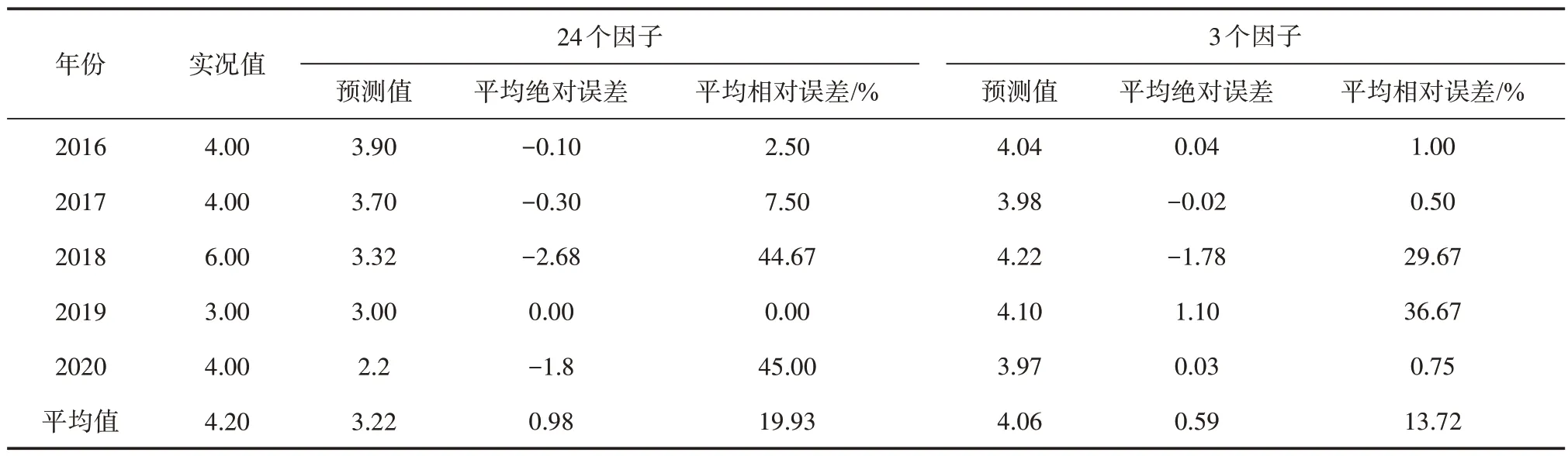
表6 2016—2020年台风频数GRU模型预报结果Tab.6 GRU model forecast results of typhoon number in 2016—2020

图5 RF模型训练集拟合预报和实况序列Fig.5 RF model training to fit forecasts and observations

2.5 GRU模型预报

本模型基于tensorflow 搭建，样本集数量较少，只包括一个隐藏层，内含20 个神经元，算法优化器选用rmsprop，使用均方误差进行误差衡量。由于特征因子之间的数值差异很小，这里不对数据进行标准化处理，而使用层处理函数进行迭代，初次迭代2 000次，步长为5，在迭代次数达到1 000次左右时拟合基本趋于平稳，因此二次实验模型迭代1 200次。当预测因子为24 个时，得到5 a 独立样本的预报平均绝对误差为0.98，平均相对误差为19.93%。当预测因子为3 个时，5 a 独立样本预测值平均为4.06，预测平均绝对误差为0.59，平均相对误差为13.72%，分别较岭回归减少了0.44和10.30%，较使用初选因子预报结果的平均绝对误差减少0.39，平均相对误差减少6.21%；GRU 方法训练集的拟合曲线和实况序列见图6，拟合曲线和实况基本吻合，对极端年份的预测结果接近实况。

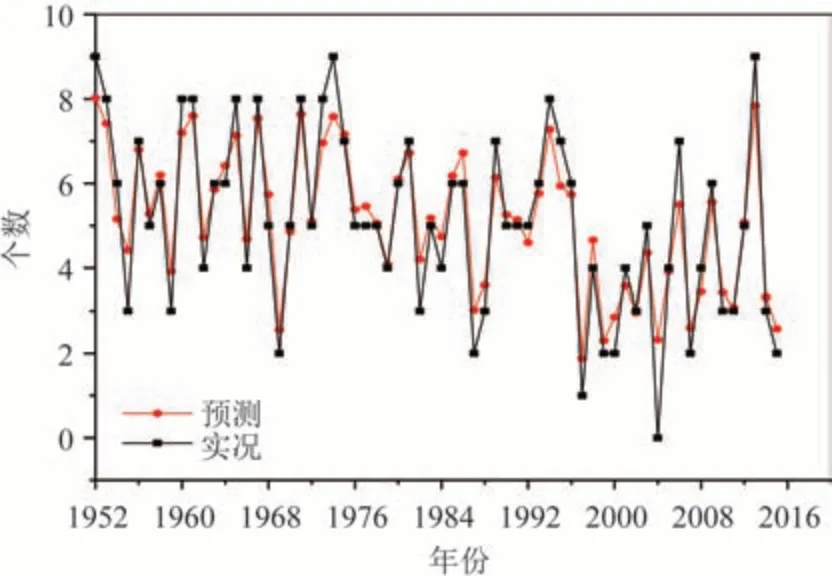
图6 GRU模型训练集拟合预报和实况序列Fig.6 GRU model training to fit forecasts and observations

3 总结与讨论

本文计算了台风频数与88项环流特征量、26项海温指数的相关系数，初次筛选出24 个高相关因子，再利用随机森林方法进行二次筛选得到3 个预报因子并建立基于3 种机器学习算法的预报模型，对训练样本集进行多次迭代计算，不断优化模型参数，对2016—2020年台风个数进行预测实验。岭回归方法、支持向量回归方法、随机森林方法和循环门单元方法的预测结果较使用初选因子平均相对误差分别减少14.11%、0.73%、2.2%、6.21%，可见利用随机森林方法对预测因子进行二次筛选是有效的，能充分发挥多信息融合的优势，在线性拟合的过程中能进一步提高数据的适应能力。由此，使用随机森林二次筛选因子建立模型，机器学习预报方法比岭回归方法的平均相对误差都有减少，其中循环门单元方法、随机森林方法、支持向量回归方法的平均相对误差分别减少10.30%，9.44%，7.47%，由此可知，机器学习方法在处理高维数据下的非线性问题上具有较大优势。在未来的工作中，我们还要考虑增加其他影响台风形成的因子，在模型分析中选择更多的预测因子，进一步优化模型参数，提高预测的精度和计算效率。