P-RSHMU蒸发波导预测与湍流通量相关性分析

张利军，张超，王红光，郭相明，韩杰，张守宝

（中国电波传播研究所，山东青岛 266107）

0 引言

近海面水汽会随着高度迅速下降而形成蒸发波导，该类型大气波导发生概率高，因此受到雷达以及电波传播学界的极大关注。这种反常的传播环境会极大地影响海洋环境中的雷达、通信、电子对抗设备的性能，尤其会使得雷达实现超视距传播或者形成雷达盲区等。从20 世纪60 年代开始，伴随着微气象学的发展，国内外的科研工作者基于海上气象观测数据，以相似理论为基础开始了蒸发波导模型的研究分析，相继提出了JESKES 模型[1]、ROTHERAM 模 型[2]、FAIRALL 模 型[3]、PAULUSJESKES 模型[4]、RSHMU（Russian State Hydrometeorological University，俄罗斯国立水文气象大学）模型[5]、MGB（Musson-Gauthier-Bruth）模 型[6]、BYC（Babin-Young-Carton）模 型[7]、NPS（Navy Postgraduate School，海军研究生院）模型[8]以及伪折射率模型[9]等。

RSHMU 模型公开发表时间较晚，针对此模型的适用性分析文献较少。由于文献[5]中的温度湿度剖面稳定度函数存在编辑错误，导致张永刚等[10-11]在错误地引用了这些剖面稳定度函数后，得到RSHMU 模型预测风速特征参数的结果较差以及温度、湿度剖面函数在南海海区不适用的结论。张利军等[12]更正了温度、湿度剖面稳定度函数的编辑错误，并基于正确的剖面稳定度函数给出了该模型在不稳定条件下的高度预测，结果优于美国NPS 模型。进一步地，张利军等[13]借鉴了PAULUSJESKES 的订正方法，给出了改进的RSHMU 模型（即P-RSHMU 模型），该模型在不稳定条件下的预测性能保持不变，稳定条件下的预测性能获得极大提高，因此基于P-RSHMU 蒸发波导模型，能够给出适合稳定条件以及不稳定条件下的合理蒸发波导高度。

郭相明等[14]基于海上梯度塔观测数据，分析了多种蒸发波导预测模型的适用性。郭相明等[15]还应用湍流通量分析了蒸发波导的形成机理，并利用TOGA-COARE 实验期间测试的1992 年11 月25—26 日的一组不稳定大气时的实验数据，定性分析了蒸发波导的生成和变化与代表湍流运动的湍流通量的关系。众所周知，海气界面通量交换是海气相互作用的重要环节，海气界面通量的确定在海气相互作用研究方面具有重要意义，受到海洋学界和气象学界的广泛重视。张超等[16]从基本的气象观测资料出发，利用经海上观测数据验证有效的耦合海洋-大气响应试验（Coupled Ocean-Atmosphere Response Experiment，COARE）通量算法[17-18]以及改进的NPS蒸发波导预测模型，计算获得了南海北部海域海面湍流通量以及蒸发波导高度，并定量分析了二者之间的相关性。由于稳定条件下低风速时改进的NPS 模型计算可能出现蒸发波导高度达40 m 的情形，进而可能影响稳定条件下蒸发波导高度与湍流通量的相关性计算，因此本文引入预测精度较高的P-RSHMU 蒸发波导模型，基于海上气象水文数据计算蒸发波导高度，有效抑制了稳定条件下蒸发波导高度预测不合理的现象。进一步地，讨论了PRSHMU 模型预测高度与张超等[16]给出的湍流通量结果的相关性。这些结果可为深入理解蒸发波导的形成机理和内涵提供参考。

1 湍流通量、蒸发波导高度计算方法

1.1 湍流通量计算方法

海气界面通量的计算方法通常分为直接计算方法和整体参数化（Bulk Parameter）方法。直接计算方法是根据通量的定义直接测量气象要素的湍流脉动量并计算其二阶矩，该方法是相对最准确的方法，但由于实际中会受到人力、物力以及观测手段的影响，因此通常采用整体参数化方法来估计海气界面的湍流通量[17]。整体参数化方法依赖于风速、温度、湿度等基本气象参数，目前普遍使用的是计算湍流通量的整体公式，较为先进且普遍认可的通量算法是COARE 算法，该算法可以计算风速、温度、比湿的特征参数，进而计算海气湍流通量。海气湍流通量关系式定义如下[18]：

式中：M为动量通量，单位：N/m2；HS为感热通量，又称显热通量，单位：W/m2；HE为潜热通量，单位：W/m2；ρ为空气密度，单位：kg/m3；cp为空气定压热容，单位：m2/（s2·K）；LE是水的蒸发潜热，单位：J/kg；w'、u'、θ'、q'分别表示垂直风速、水平风速、位温、比湿的湍流脉动值；u*、θ*、q*分别为莫宁奥布霍夫相似（Monin-Obukhov Similarity，MOS）理论中的风速、位温、比湿特征量。

1.2 P-RSHMU蒸发波导高度计算方法

蒸发波导高度采用P-RSHMU 模型[13]计算。近地层的温度剖面以及比湿剖面计算公式如下[19]：

式中：Tsea、qs分别为海表温度（单位：K）以及海面比湿（单位：kg/kg）；θ*、q*分别为位温特征量、比湿特征量；κ为卡曼常数，取0.4；z0θ、z0q分别为温度粗糙度和比湿粗糙度分别为温度普适函数和比湿普适函数；Γd为干绝热递率，取0.009 76 K/m；z为高度，单位：m。

需要特别指出的是，温度和湿度剖面稳定度函数的正确表达式为[12]：

式中：β1= 8；y1=(1 -β2ξ)13；β2= 35；γ2= 6。

大气压力剖面由流体静力学公式以及理想气体定律联合确定，积分得到如下压力剖面公式[19]：

式中：R为干空气理想气体率常数287.04 J/（kg·K）；为层高度z1和z2处平均虚位温。

由比湿以及压力剖面计算水汽压e剖面[19]：

式中：ε为干空气气体常数以及水汽常数之比，取0.621 7）。一旦确定了温度、水汽压、压强剖面，修正折射率[19]剖面可以按照下式计算得到：

通过寻找M 剖面中的最小值即可确定对应的蒸发波导高度。进一步地，当气海温差小于-1 ℃时，采用RSHMU 模型计算方法；当气海温差大于-1 ℃时，保持海温不变，利用RSHMU 模型分别计算气海温差等于-1 ℃以及等于0 ℃的蒸发波导高度h-1和h0，如果h0>h-1，则蒸发波导高度为h-1，否则依照原来的气温与海温来计算蒸发波导高度[13]。该方法即为蒸发波导P-RSHMU模型的计算方法。

2 数据资料与计算结果

2.1 数据资料

依托广东茂名博贺海洋气象科学试验基地的海上试验平台[20]，采用要素集成的气象传感器以及海温传感器，以分钟级为单位，采集了2017 年11 月26 日—2018 年5 月31 日的气象数据，包含气温、海温、相对湿度、气压、风速、风向、降雨量等数据，共计262 769 组。剔除湍动分量的影响，对分钟级的气象要素进行小时平均，获得小时的气象要素分布，共计4 395组。

基于P-RSHMU 模型计算获得小时蒸发波导高度，结果见图1。由图可见，大部分蒸发波导高度位于0～20 m，没有出现蒸发波导高度为40 m的现象，波导高度曲线呈现连续变化。而张超等[16]基于改进的NPS模型计算出的蒸发波导高度在5月中下旬风向稳定的时段，可能出现极其稳定的条件，此时蒸发波导高度为40 m，且呈现跳跃变化。为对比起见，图2 给出该模型计算结果与改进的NPS 模型的结果对比图，由图可见，大部分情形下二者一致性较好，P-RSHMU 模型有效抑制了蒸发波导高度较高尤其预测的蒸发波导高度为40 m的情形。

图1 蒸发波导高度计算结果Fig.1 Calculation result of evaporation duct height

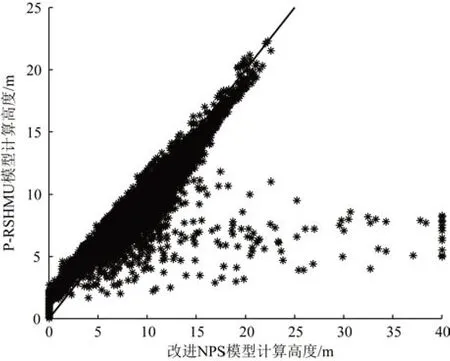
图2 不同模型计算结果对比Fig.2 Comparison of calculation result between different models

2.2 相关性分析

将计算的蒸发波导高度与潜热通量、感热通量、动量通量作散点图，由图3 可见，蒸发波导高度与潜热通量以及动量通量呈现某种线性关系，而与感热通量的线性关系不明显。进一步地，计算蒸发波导高度与潜热通量、感热通量、动量通量的相关系数分别为0.92、-0.12、-0.41。

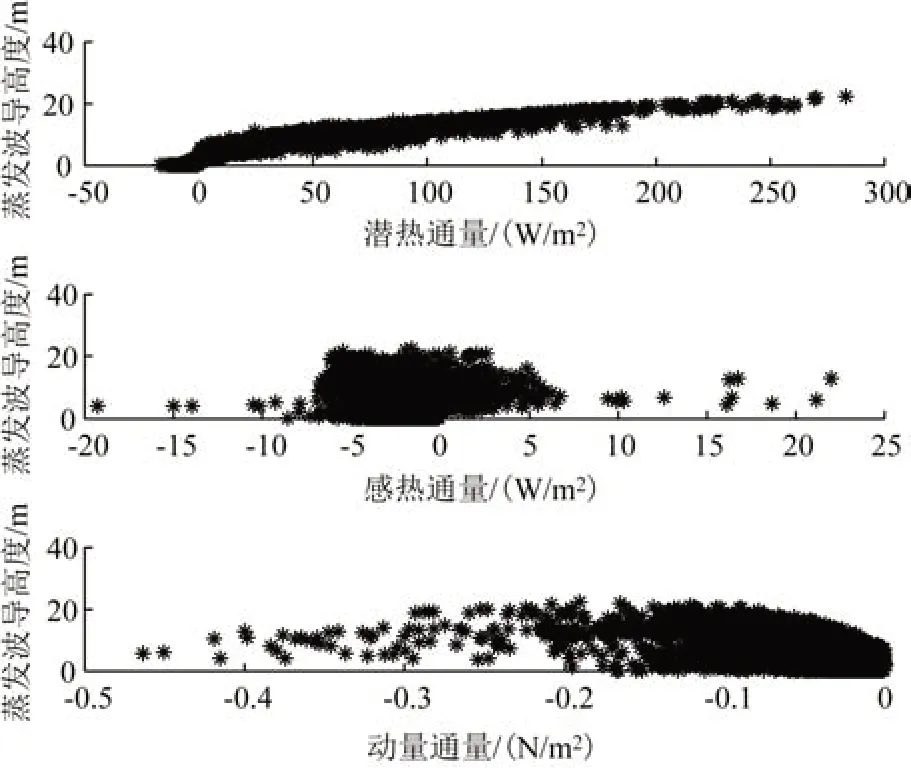
图3 湍流通量与蒸发波导高度散点图Fig.3 Scatter plot of turbulent flux and evaporation duct height

以大气温度与海水温度之差为标准区分稳定条件，并分别给出不稳定条件（气海温差＜0 ℃）、中性条件（气海温差=0 ℃）、稳定条件（气海温差＞0 ℃）下的蒸发波导高度与湍流通量的散点图，结果如图4—6。不稳定条件（见图4）以及中性条件下（见图5）的散点图与张超等[16]研究结果类似，而稳定条件下（见图6）的散点图显著不同于文献[16]，图7给出了稳定条件下文献[16]的散点图进行对比。

图4 不稳定条件下湍流通量与蒸发波导高度散点图Fig.4 Scatter plot of turbulent flux and evaporation duct height under unstable condition

图5 中性条件下湍流通量与蒸发波导高度散点图Fig.5 Scatter plot of turbulent flux and evaporation duct height under neutral condition

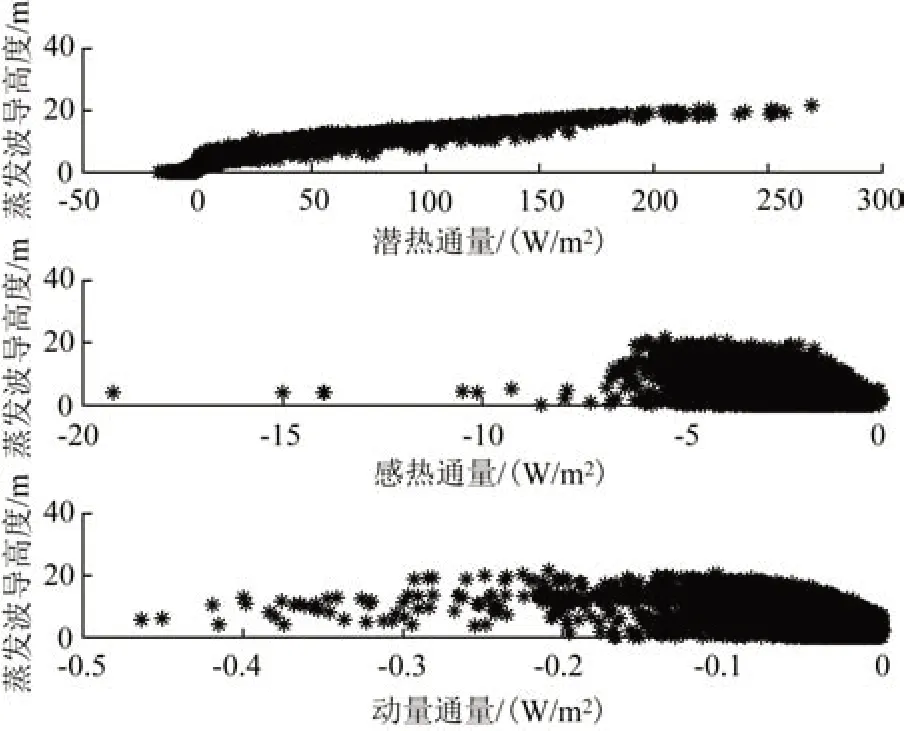
图6 稳定条件下湍流通量与蒸发波导高度散点图Fig.6 Scatter plot of turbulent flux and evaporation duct height under stable condition

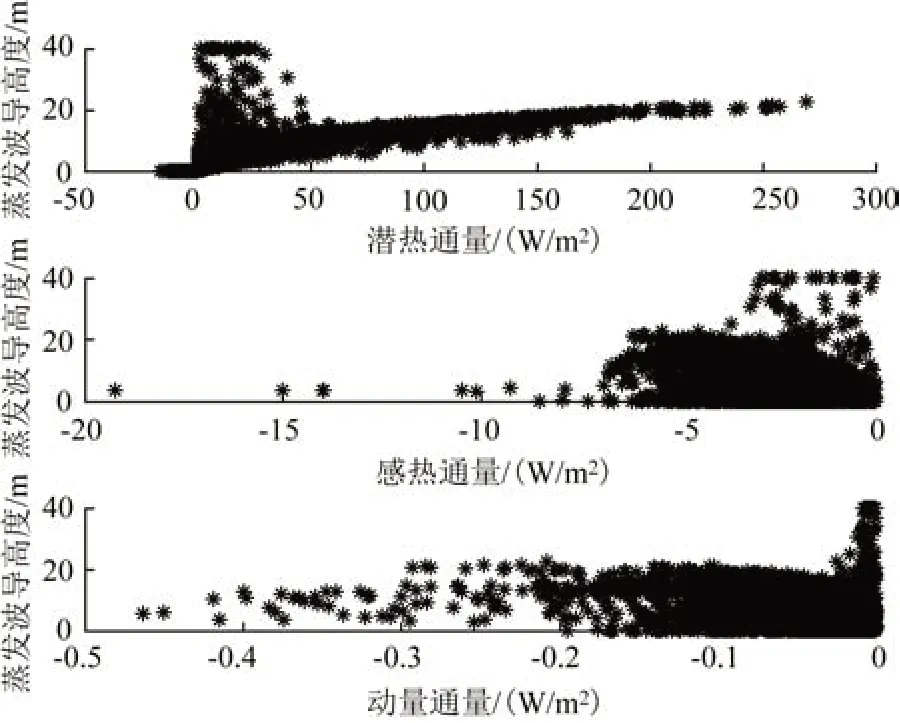
图7 稳定条件下的计算结果（引自文献[16]）Fig.7 Calculation result under stable condition(cited from literature[16])

张超等[16]指出，40 m 的蒸发波导高度存在于0 N/m2动量通量、-3～0 W/m2感热通量以及0～40 W/m2潜热通量附近。动量通量较小，对应风速较小，感热通量为负，对应感热由上面的大气向下面的海洋传输能量，即气海温差＞0 ℃，因此在稳定条件下，较低的风速导致蒸发波导高度的预测效果较差。这可能与该条件下湍流输运不够旺盛进而导致蒸发波导预测理论MOS 中假定近海面空间为常通量不成立有关。

文中引入的P-RSHMU 模型则有效地避免了稳定条件下预测蒸发波导高度不合理的现象，在稳定条件下同样可以获得与不稳定条件、中性条件一致的预测结果。区分不同稳定性条件下蒸发波导高度与湍流通量的相关系数见表1，其中稳定条件计算样本数为3 969，中性条件为16，不稳定条件为410。由表中数据可以看到，在不区分稳定性条件下，潜热通量与蒸发波导的高度最相关，动量通量次之；不稳定条件下，两者具有一致的相关性特征；中性条件下，感热通量的相关性次之；稳定条件下，动量通量的相关性次之。整体来说，潜热通量对应着水汽相变直接影响蒸发波导的生成，动量通量又或快或慢地影响海面水汽蒸发进而间接影响蒸发波导的生成，感热通量仅仅代表由于温度差异导致海洋向大气或者大气向海洋输送的热量，对整体的湍流通量贡献较小，因此潜热通量、动量通量与蒸发波导高度的相关系数大于感热通量。

2.3 对比分析

作为对比，表1还列出了文献[16]的相关系数结果。由表中数据可以看到，引入的P-RSHMU 模型显著改变了稳定条件下即气海温差＞0 ℃时湍流通量与P-RSHMU 蒸发波导高度的相关系数，计算结果较为合理。

需要特别指出的是，稳定条件下改进的NPS 模型在气海温差＞0 ℃时以及动量通量较小（或者风速较小）时会出现蒸发波导高度为40 m 或者计算波导高度偏高的现象，导致该条件下计算的蒸发波导高度与潜热通量的相关系数为0.73，而P-RSHMU模型则抑制了这种现象的出现，进而二者的相关系数提高到0.92，且保持了与不稳定条件以及中性条件一致的计算结果，即蒸发波导与潜热通量显著相关。

通常情况下蒸发波导被认为是由于近海面水汽蒸发从而引起大气湿度随高度锐减而形成的一种大气层结。近海面水汽可认为是饱和的，随着高度的增加，相对湿度迅速下降进而形成蒸发波导。而潜热通量是由于水汽相变向大气传输的热量通量，因而文中计算的蒸发波导高度与潜热通量的相关系数为0.92，有力支撑了蒸发波导的形成原因。

3 结论

本文基于海上平台观测的水文气象数据，利用不同稳定性条件下预测效果都较好的P-RSHMU 模型，计算获得不同时刻的蒸发波导高度，有效抑制了稳定条件下蒸发波导预测高度为40 m 或者预测偏高的不合理现象。进一步地，分析了该模型预测蒸发波导高度与动量通量、感热通量、潜热通量等湍流通量参数的相关性，结果表明蒸发波导高度与潜热通量高度显著相关，相关系数可达0.92，与动量通量相关性次之，相关系数为-0.41，与感热通量的相关系数最小，为-0.12。这些结果进一步为丰富蒸发波导的内涵以及形成机理提供重要数据支撑。