基于优化随机森林的海基站水下声学定位模型研究

徐 剑，金康康，李中政，王 岚，张朝怡，刘 毅

基于优化随机森林的海基站水下声学定位模型研究

徐 剑1，金康康1，李中政2，王 岚1，张朝怡1，刘 毅1

(1. 天津大学海洋科学与技术学院，天津 300072；2. 海军研究院，天津 300061)

海洋声学目标探测技术在海洋资源开发、海洋生物保护、区域海洋生态监测及军事领域等方面都具有无可替代的优势．然而，接收传感器常常会受到外界干扰声源的影响，从而导致定位性能下降．为解决这一问题，本文提出了一种基于优化随机森林的海基站水下声学定位模型来改善定位准确度．首先，对采集的原始信号进行数据预处理．对于信号无干扰采集数据，仅保留有效的样本，剔除包括缺失、异常、相同或相似的数据．对于信号干扰下采集数据，先对异常情况进行分类，然后去除存在干扰的基站数据．利用主成分分析对数据进行降维，并将综合特征作为高斯混合聚类的输入．为确定最优超参数，采用网格搜索和交叉验证的封装模块并设置混合系数，然后构建基于优化随机森林的水下声学定位模型，并将其与多点空间定位模型进行对比．实验结果表明，在信号无干扰和有干扰条件下，采用多点空间定位模型计算出目标三维定位误差RMSE分别为5.648m、26.264m，而采用本文模型预测的RMSE分别为0.232m、4.354m．所提出的方法显著提高了目标的定位精度，并具有较强的泛化能力．且在无干扰条件下，对于、及方向的估计，所提出的方法的RMSE分别为0.122m、0.099m和0.171m．而在有干扰条件下，对于、及方向的估计，RMSE分别为1.715m、1.691m和3.627m．特别是方向的定位误差最大，与实际情况相吻合．以上数据结果验证了所提出方法的有效性，为水下运动目标高精度定位及定位导航系统的论证设计提供了新的思路．

水下声学定位；多基站；到达时间差；优化随机森林；高斯混合聚类

卫星导航系统的快速建设与发展，能够通过低轨实现全覆盖[1-2]，但由于电磁波在海洋中衰减过快，不能进行远距离传输[3-5]．声波是开发和研究海洋资源的重要载体，伴随着自然资源消耗量的不断增加，海洋声学目标探测技术对确保区域海洋环境安全及加深对海域理解和探索有着不可替代的优势．因此，对于水下声学目标探测技术的深入研究成为目前海洋测绘领域的关切课题[6-7]．水下声学定位方法主要包括匹配场处理、目标运动分析及多基站交会定位等，基于信号到达时间差(time difference of arrival，TDOA)的多基站水下定位方法使用更为广泛. TDOA定位技术[8-9]依赖于精确的基站位置及准确的声速，只需要控制各个接收节点之间的时间同步，便可通过解析式解算出水下声学目标位置．

然而，在实际测量中，海基站的位置参数可能由于人为误差、外界干扰、不可预测的海流等因素引入偏差[10-13]．特别地，在海洋环境中存在着各种障碍物的散射、环境噪声、多径效应等，使得声波在传播过程中丰富性和不确定性增加，因此声速并不能直接以常数形式代入[13]，从而限制了定位模型的应用范围，同时对海基站的布放规则及设计提出更高要求[14].因此，针对复杂的海洋环境，获得高精度的水下声学目标位置信息亟待探讨．

本文提出一种基于优化随机森林的海基站水下声学定位模型，以完成干扰信号条件(即接收传感器受到外界环境振动冲击或外界干扰声源影响)下的高精度定位．首先对采集的原始信号进行预处理，包括异常数据的分类和无用数据的剔除．利用PCA降维，将两个综合特征作为高斯混合聚类模型的输入，对基站接收数据异常情况进行预报．然后，分别对正常数据和异常数据构建目标位置预测模型，并对比多点空间定位模型与优化随机森林模型的预测效果，验证所提出方法的有效性及鲁棒性，以期为定位导航系统的论证设计提供参考.

1 数据准备与预处理

1.1 采集数据

理论上，布放的海基站越多，定位精度越高，但也增加了设备成本．为此，本文以典型的四基站为例开展高精度的水下声学目标定位模型的研究[15]．多基站水下定位仿真示意如图1所示．考虑长500m、宽500m、深300m的定位水域应用范围，海底平坦，在海底布放多个已知坐标的锚基站．锚基站接收并处理从目标物体发射过来的信号，进而估计基站与定位目标之间的距离．在信号无干扰和有干扰条件下，采集定位目标在测量海区内不同位置的数据，共得到156298条记录，数据格式为ASCII文本．

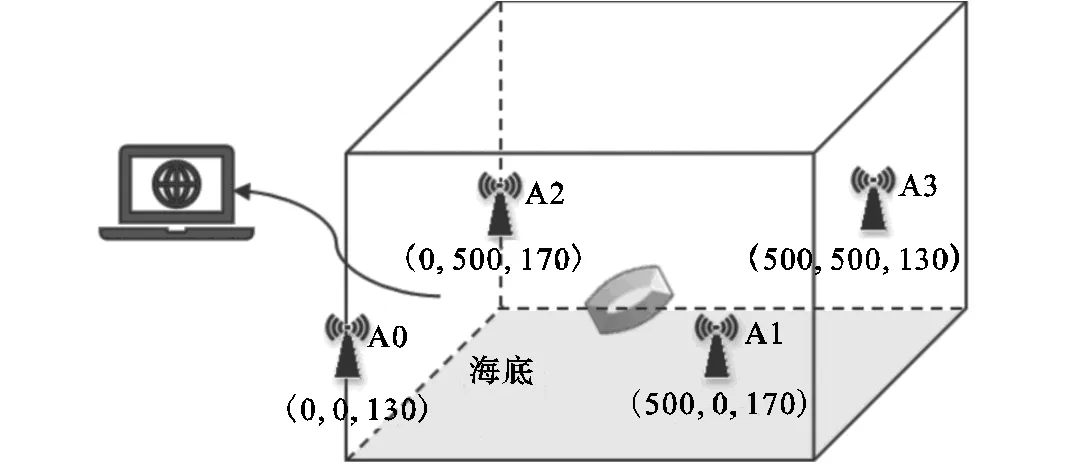
图1 多基站定位系统示意

1.2 数据预处理

为了高效利用空间大数据，对采集数据文本进行预处理．首先，将采集到的数据提取出来，并转换为二维矩阵形式，以便进行后续的处理和分析．然后，针对数据异常产生的原因，分别对信号无干扰和有干扰下采集的数据进行数据清洗操作[16-17]．在信号有干扰条件下，首先对采集的数据进行分类，以判断海基站是否存在异常．通过对数据进行分组或标记，确定异常的基站．然后通过删除缺失、异常数据(粗差)、相同和相似数据样本来提升数据质量．对于信号无干扰条件下采集的数据，仅需要删除缺失、异常数据(粗差)、相同和相似数据样本．

在对采集的数据经过分析后，设置条件判断，将同一个文本中数值相同的样本剔除，避免相同数据对模型训练的影响．其次，针对接收的定位数据中每个样本的编号，以4个基站数据为1组判断编号是否连续．若不连续，则视为该基站存有数据缺失问题，并直接剔除本组数据．此外，采用余弦相似度和3原则对异常值进行处理．

余弦相似度是通过测量两个向量夹角的余弦值来度量它们之间的相似程度，数学表达式为

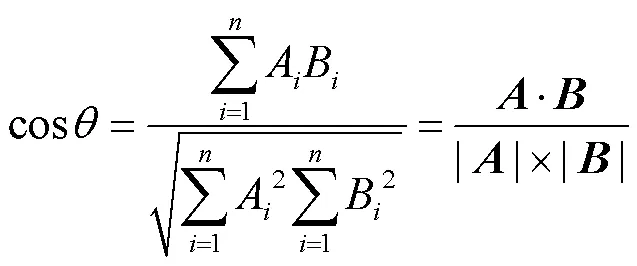
式中、为维空间中的两个向量，由余弦相似度公式得两个向量之间的相似度取值范围为[-1，1]．为了对数据进行筛选，需要确定一个合理的阈值来衡量相似度的要求，并将不满足阈值要求的数据剔除掉．

3原则是一种常用的统计方法，适用于满足正态分布假设的数据集．根据该原则，将采样点与数据集平均值的差的绝对值与3倍标准差比较，去除与平均值偏离过大的异常值．

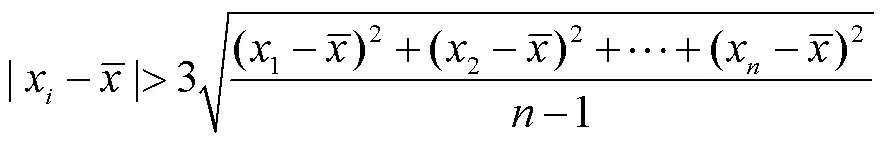
此处针对采集的数据先进行统计分析，从图2中可看出所检测的定位数据满足正态分布．s代表标准差，μ代表均值．x落在(μ－3s，μ＋3s)以外的概率小于0.3%，在实际问题中常认为相应的事件是不会发生的，基本上可以把区间(μ－3s，μ＋3s)看作是随机变量X实际可能的取值区间．通过应用3s原则，对计算得到的余弦相似度进行异常数据处理．经过处理后，数据量基本保持不变，因此本文选择提取落在区间的数据．图3展示了在信号无干扰情况下经过处理后的数据结果．

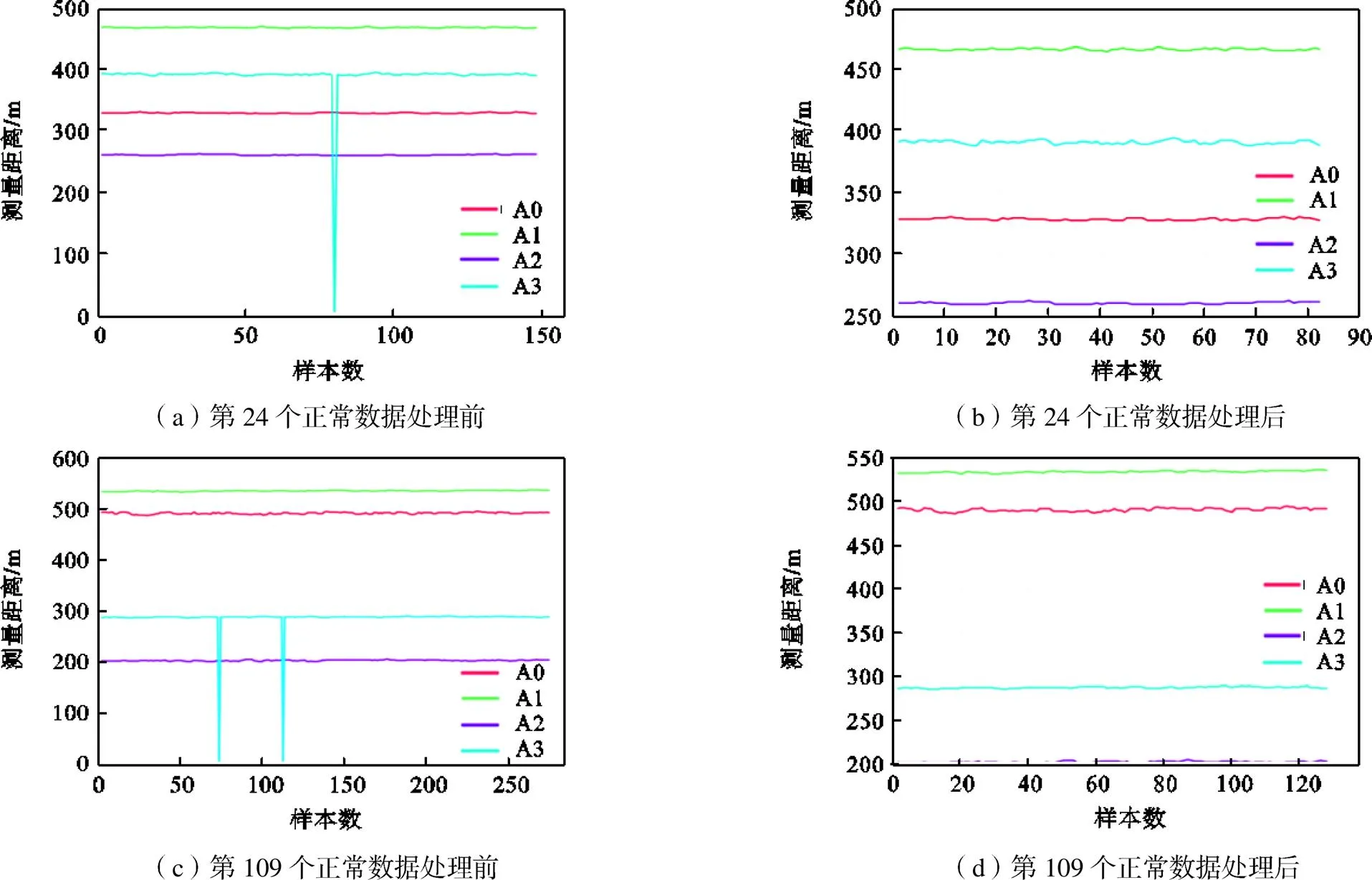
图3 正常数据处理结果

当信号存在干扰时，在连续的时间段上会有一个海基站与水下声学目标之间的测距值产生异常．由此，根据海基站不同，可将异常情况分为4类，如表1所示．

表1 异常情况分类

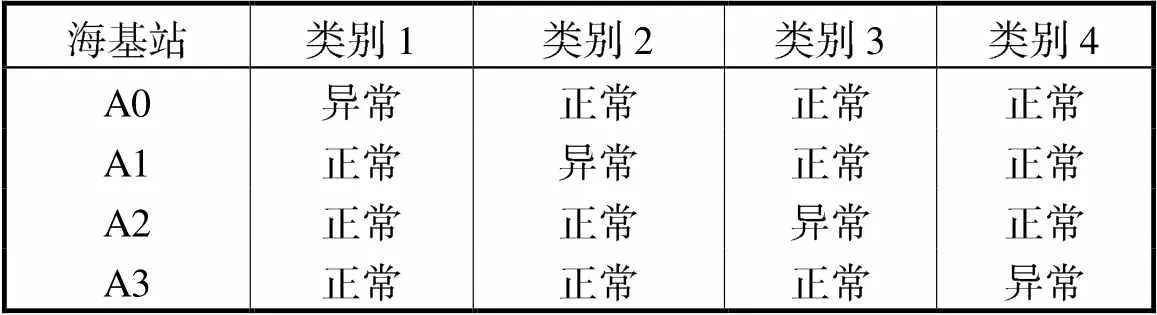
Tab.1 Classification of exceptions

根据数据文件中的时间戳信息对异常数据进行分类，并分析不同时间段数据异常的原因．在将数据划分为多组连续时间段时，存在两种情况：距离测量值的跳跃和独立的随机变化．通过统计每个连续时间段内4组距离观测值的方差个数以了解异常情况的特点．

如果方差个数大于1，表示存在距离观测值的跳跃．通过设定适当的阈值，找到跳跃点，并将时间段进一步划分为较小的连续时间段；如果方差个数为1，则说明数据变化是独立的随机变化，此时无需对时间段进行进一步划分[18]．最后统计各个连续时间段内的4组距离观测值中的方差，方差最大代表该基站接收到异常数据．在有信号干扰下，数据处理结果如图4所示．

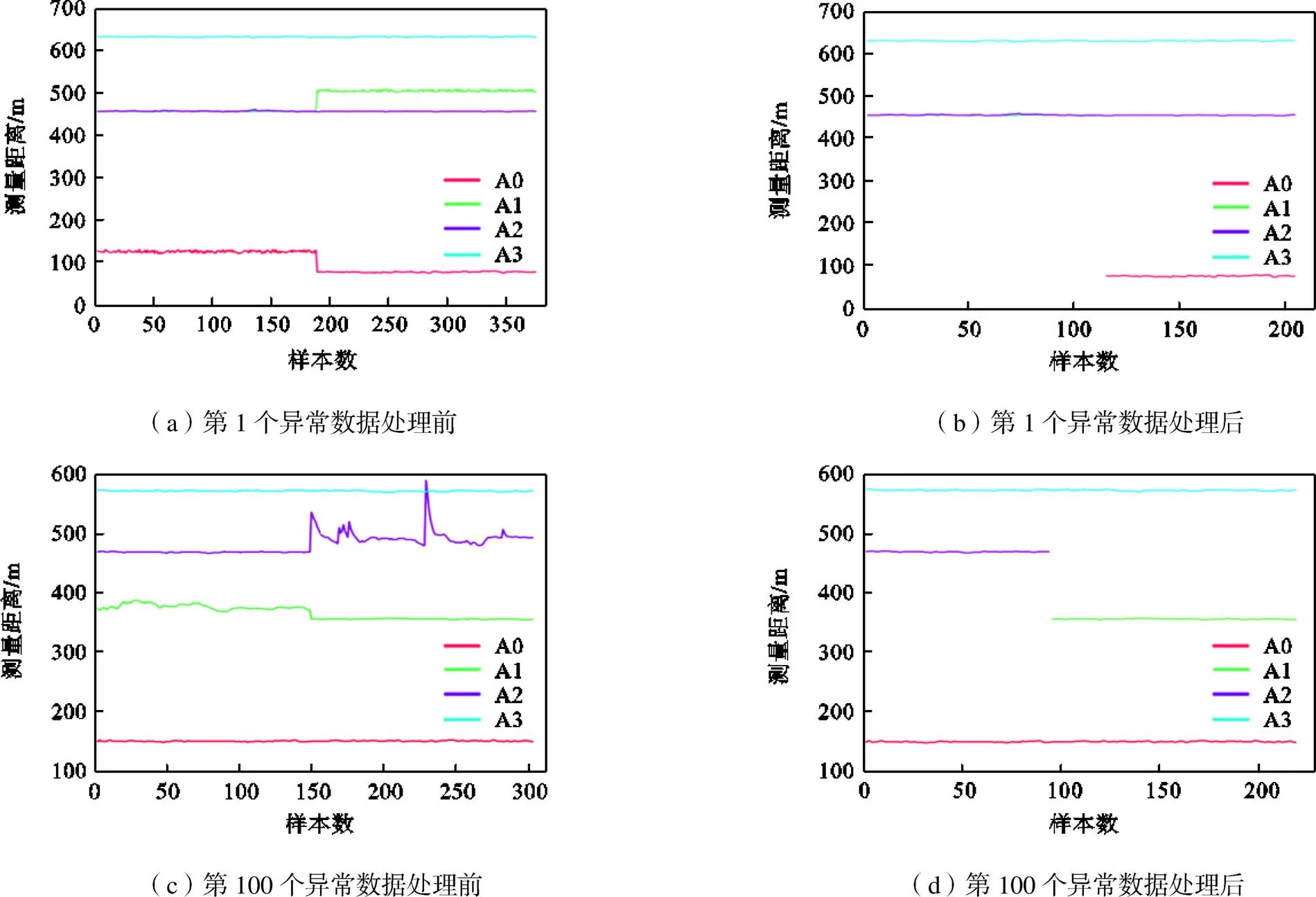
图4 异常数据处理结果

2 基于优化随机森林的海基站水下声学定位模型构建

2.1 实验原理

2.1.1 多点空间定位过程

利用测量距离建立一系列方程组，并求得以各基站为圆心、测距为半径的圆周的两两相交线[19]，4个球的交点坐标即为探测目标的位置，多点定位的原理如图5所示．

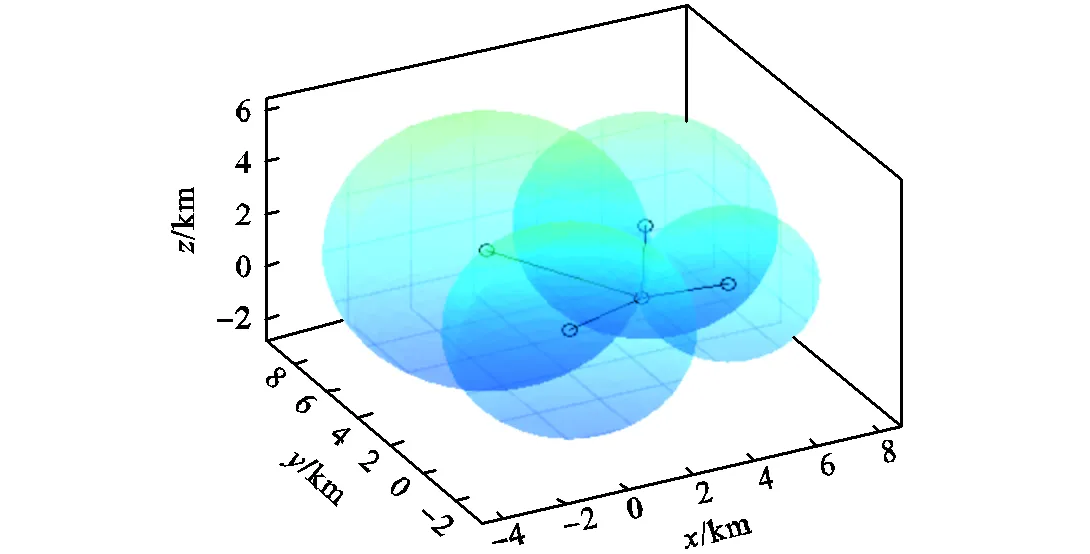
图5 空间定位原理分析

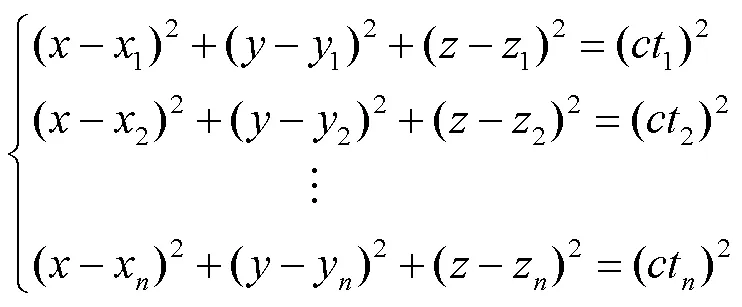
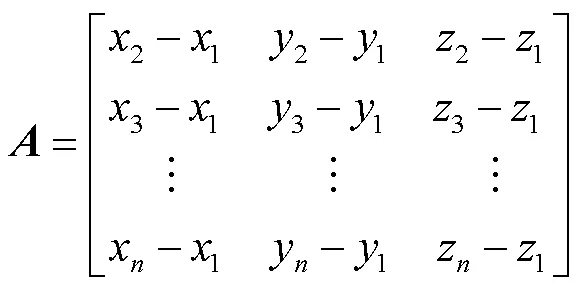
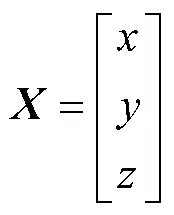
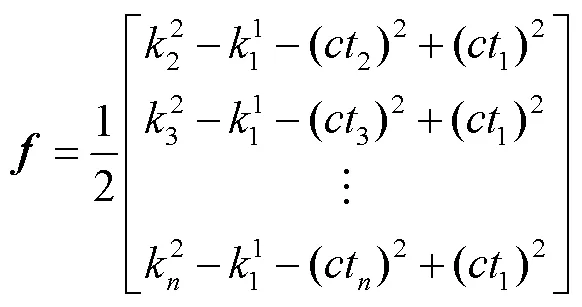
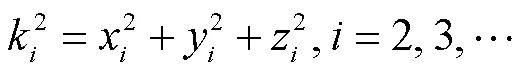
若矩阵的逆矩阵存在，则水下声学目标的坐标向量为

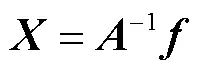
2.1.2 随机森林算法

随机森林(random forest，RF)算法是由Leo Breiman提出的以分类回归树为基学习器的集成学习模型[20].该算法调节参数少，对噪声和异常值的容忍度高，具有较强的抗干扰能力，尤其在解决大量样本、具有高维度特征或多分类问题时被广泛应用．利用自助聚集策略，从原始样本数据中提取多个样本建立多个决策树，结合所有子树的预测结果得到一个更加准确和稳定的结果．随机森林算法[21-22]流程如下．

步骤1指定值．由于在每棵决策树分裂的过程中，不是样本中全部个特征属性都参与分裂，而是从中随机抽取个变量，同时分裂过程中特征属性的选择需满足节点不纯度最小原则；

步骤2应用 Bagging 随机取样法在原始训练集中有放回地随机抽取个样本集，组成棵决策树，避免陷入局部最优解；

步骤3重复步骤1、2，建立多棵回归决策树，以构成森林；

步骤4对于棵决策树输出的预测值取平均即为目标位置．

从随机森林的评估过程中可以看出，随机森林的构建过程中掺入了随机性，从而降低了随机森林过拟合现象的产生．训练RF本质是训练多个二叉决策树，在训练二叉决策树时需考虑如何切分特征、切分点及怎样衡量一个切分特征、切分点的好坏，而不纯度函数可以很好地反映出此性能．

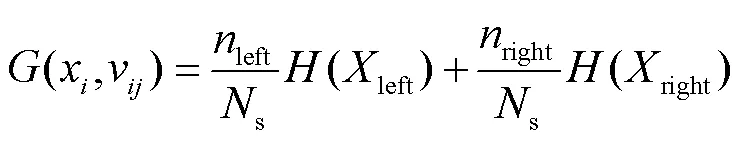
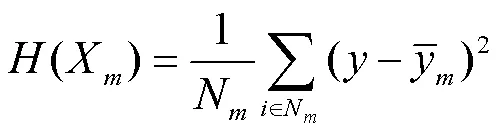
对于某一切分点，则有

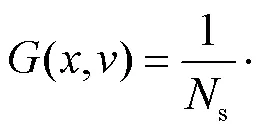
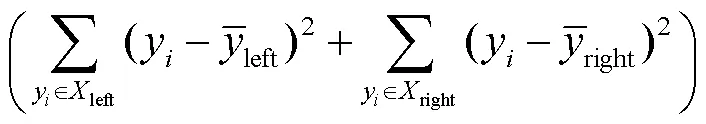
将正常数据和异常数据分别按比例分为训练集和测试集，其中测试集占数据集的30%，并进行随机抽取．然后通过随机森林算法对数据进行训练和测试，参数选择是影响模型效果的最关键因素．它可以有效防止过拟合，提高模型的泛化性能．所以在建模前对其参数进行调优是非常必要的．

RF模型中生成树数目、树的最大深度和候选分裂属性数会影响模型性能[23]．增加生成树的数量可以提高模型的稳定性和预测精度，但超过某个阈值后增加树的数量不会进一步提高准确性，反而会降低模型效率．较大的树深度有利于学习样本的特定关系，但深度过大可能导致过拟合．候选分裂属性数影响模型的随机性，由于本实验中信号数据集样本特征量较少，因此设定候选分裂属性数为None，使每棵树可以选取所有特征．

为了自适应地优化参数，采用了基于网格搜索方法(GridSearchCV)的策略．该方法将网格搜索和交叉验证结合在一起，通过穷举法遍历模型中设置的所有参数，生成一个包含所有可能参数组合的“网格”. 通过遍历这个网格中的参数组合，可以找到最优的参数配置，以进一步优化模型的性能．而在优化过程中，将每个参数组合应用于决策树训练，并使用交叉验证评估模型的表现．交叉验证的核心思想是将待分类数据集切分为多个子集，一部分作为训练集，一部分作为验证集．通过多次改变训练集和验证集的划分，降低结果的随机性．常见的折交叉验证方法就是将数据集划分为个子集，每个子集轮流作为验证集，其余子集作为训练集．计算每次验证的错误率，并将计算次预测指标的平均值作为最终结果．根据优化后的结果确定了模型的最佳参数配置．

2.2 正常数据与异常数据的判别

在实现水下声学目标精确定位过程中，判断信号是否存在干扰是至关重要的．考虑异常数据集中有且仅有一个基站与目标之间有信号干扰，因此总体样本数据被分为5类，即无信号干扰、基站1有信号干扰、基站2有信号干扰、基站3有信号干扰和基站4有信号干扰．这可以被视为一个单标签多分类问题，其中每个样本对应的预测标签只有一个，但是标签的取值可能有多种情况，即每个实例可能属于(＞3)种不同的类别．

由于缺乏信号的先验知识，采用无监督分类方法来判断数据的正常与否．无监督分类是将没有类别标签的样本聚集成不同的组，这些组称为簇，通过对每个簇的描述来对数据进行分类．无监督分类的目标是确保同一簇内的样本彼此相似，而不同簇之间的样本则应该有明显的差异．在本文中，采用了高斯混合聚类方法[24]来进行无监督学习，步骤如下．

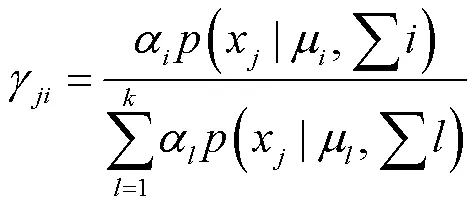
步骤4 根据均值、协方差定义及步骤3求出的后验概率，更新均值和协方差矩阵．

步骤5 重复步骤3、4，直到高斯混合模型小于收敛域值或达到最大迭代次数．

步骤6 根据计算得到的后验概率将样本划分到后验概率最大的簇中．

为了应对维度增加所带来的计算复杂度提高[25]，在进行高斯混合聚类之前采取了降维处理．首先，利用PCA将原始的4维特征重构为2维特征，以减少数据的维度，在降低计算复杂度的同时保留数据的关键信息．之后建立高斯混合聚类模型来区分在信号无干扰下采集的数据和在信号干扰下采集的数据．图6展示了模型的分类效果，可见模型能够有效地将数据分为不同的类别，为后续的定位任务奠定了基础．

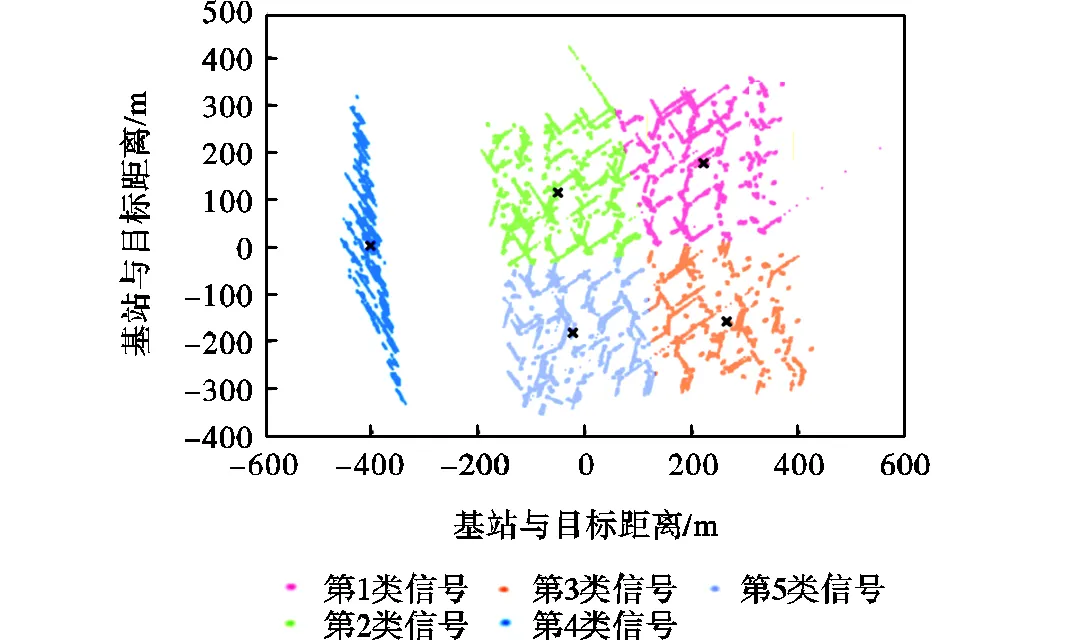
图6 采集信号数据类别图

2.3 结果对比分析

对于回归类问题，描述算法或模型性能常用的综合评价指标如下.

(1) 均方根误差(root mean square error，RMSE)

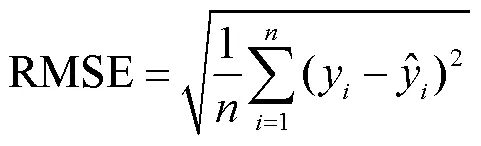
(2) 均方误差(mean square error，MSE)

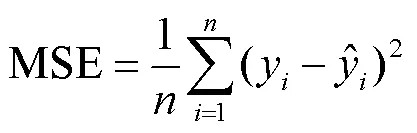
为了验证优化随机森林模型的准确性，将模型预测的结果分别与利用多点空间定位原理计算出的目标位置坐标进行对比，进而验证该模型的真实性和有效性．使用随机森林和多点空间定位原理进行预测，并得到了各种评价指标的结果，如表2所示．

在实验过程中，收集了4个海基站到水下声学目标的距离数据，每个机会节点可选择的特征数量为4个．模型的输出是对水下声学目标的三维坐标进行预测．根据计算结果，得到了各种统计误差指标，包括整体的RMSE和MSE，在二维平面上的RMSE和MSE，以及分别针对、和维度的RMSE和MSE．具体数值如表２所示．从表２和图7、8可以观察到，在基站正常的情况下，多点空间定位模型计算的RMSE为5.648m，MSE为32.000m；在二维平面上的RMSE为0.732m，MSE为0.500m；而在单个维度上，、和的RMSE分别为0.526m、0.509m和5.600m．相比之下，采用优化随机森林模型计算出的RMSE为0.232m，MSE为0.053m；在二维平面上的RMSE为0.157m，MSE为0.025m；而在单个维度上，、和的RMSE分别为0.122m、0.099m和0.171m．

表2 两种模型定位精度对比

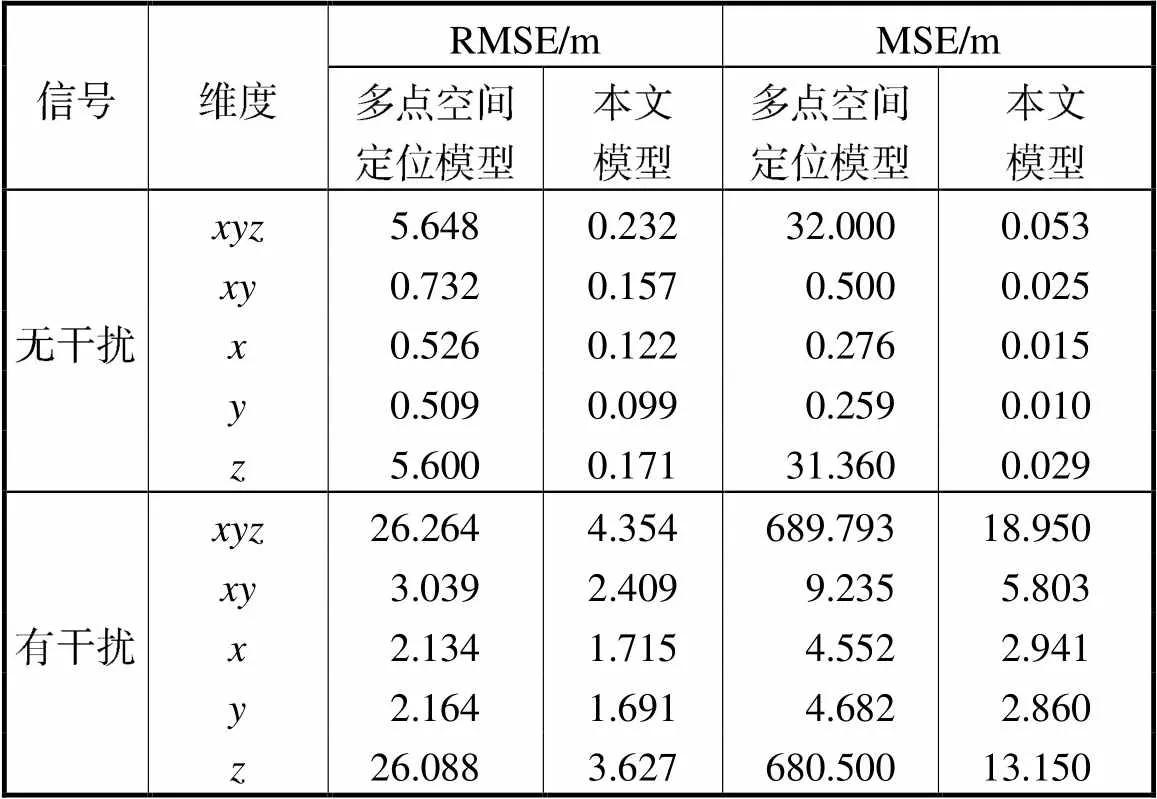
Tab.2 Comparison of the positioning accuracy between two models

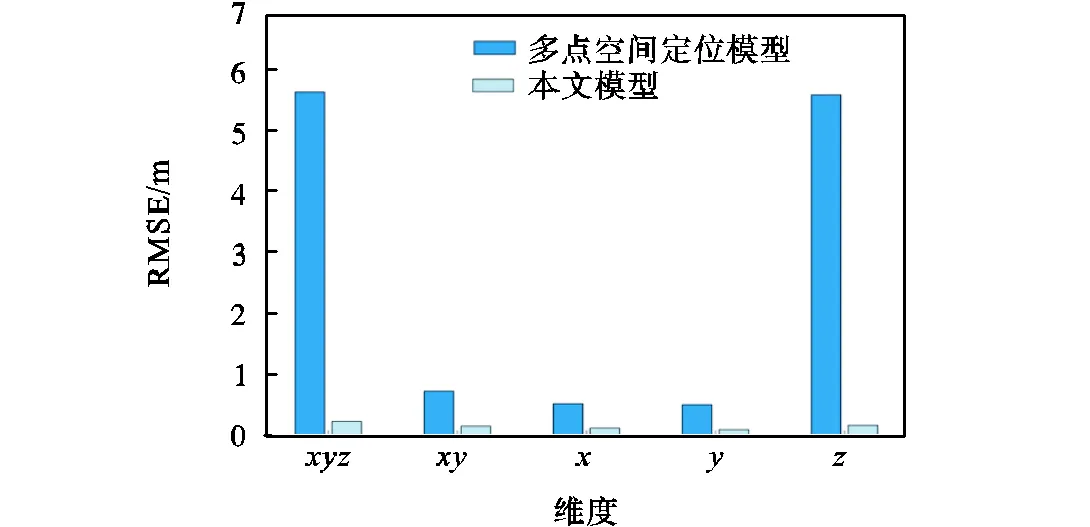
图7 基站正常RMSE实际值与预测值对比

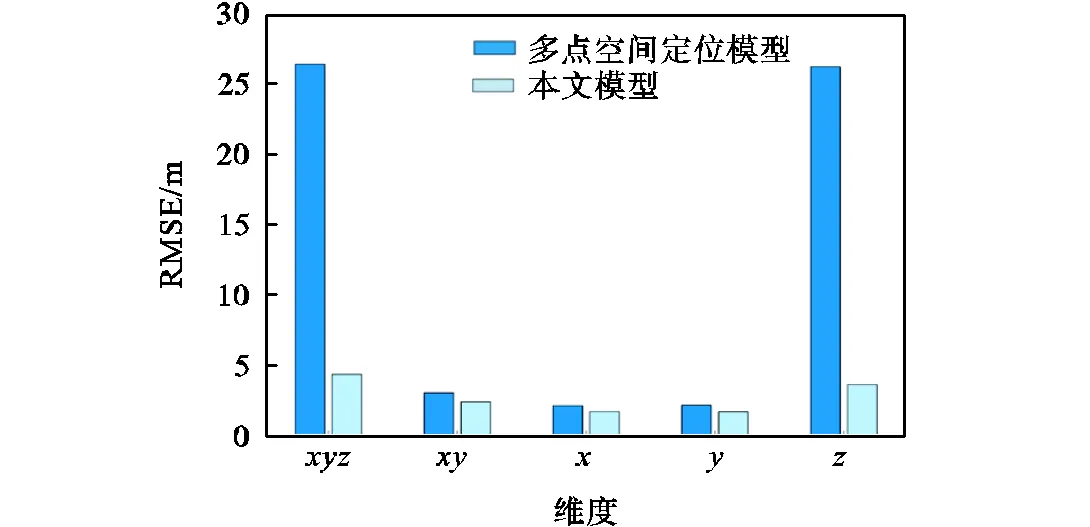
图8 基站异常RMSE实际值与预测值对比

在基站发生异常的情况下，采用多点空间定位模型计算出的误差统计特性如下：整体的RMSE为26.264m，MSE为689.793m；在二维平面上的RMSE为3.039m，MSE为9.235m；而在单个维度上，、和的RMSE分别为2.134m、2.164m和26.088m，MSE分别为4.552m、4.682m和680.500m. 相比之下，采用优化随机森林模型计算出的误差统计特性如下：RMSE为4.354m，MSE为18.950m；在二维平面上的RMSE为2.409m，MSE为5.803m；而在单个维度上，、和的RMSE分别为1.715m、1.691m和3.627m，MSE分别为2.941m、2.860m 和13.150m．通过图9和图10可以观察到，在实验中，方向的误差相较于和方向的误差大，这与实际情况相符．随机森林模型明显优于传统的基于多点空间定位原理的方法．此外，在存在信号干扰的情况下，该模型仍具有较强的抗干扰能力，能够准确地预测定位结果，进一步验证了所提出模型的可靠性和鲁棒性．

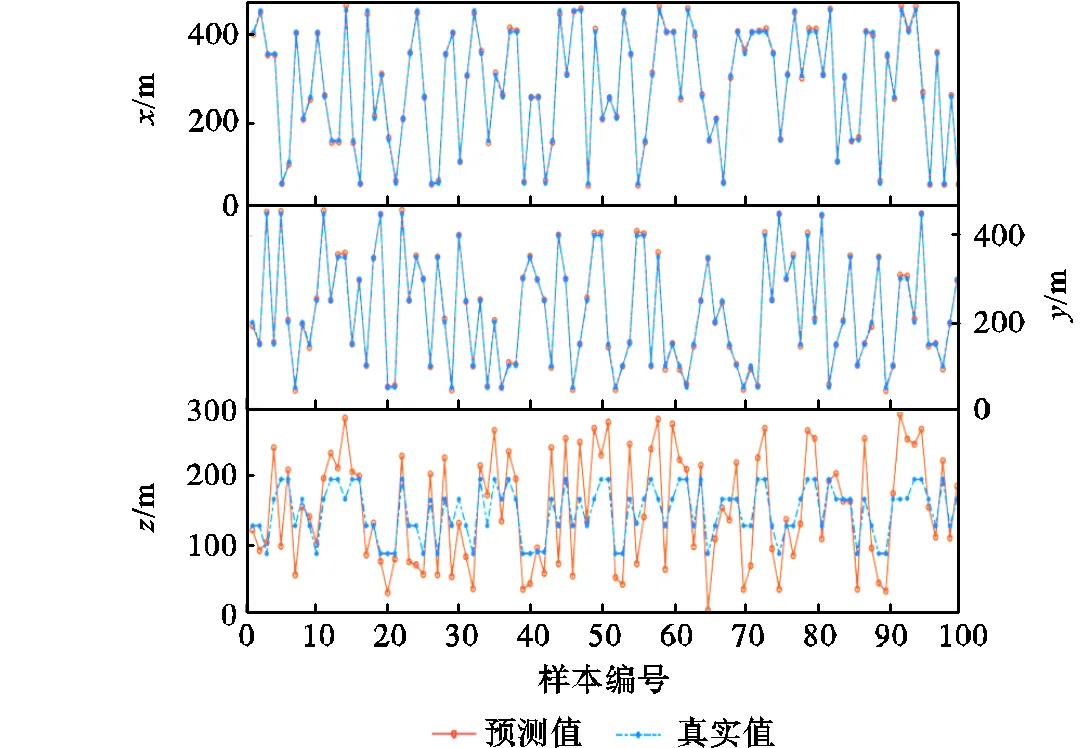
图9 无干扰下优化随机森林模型测试结果

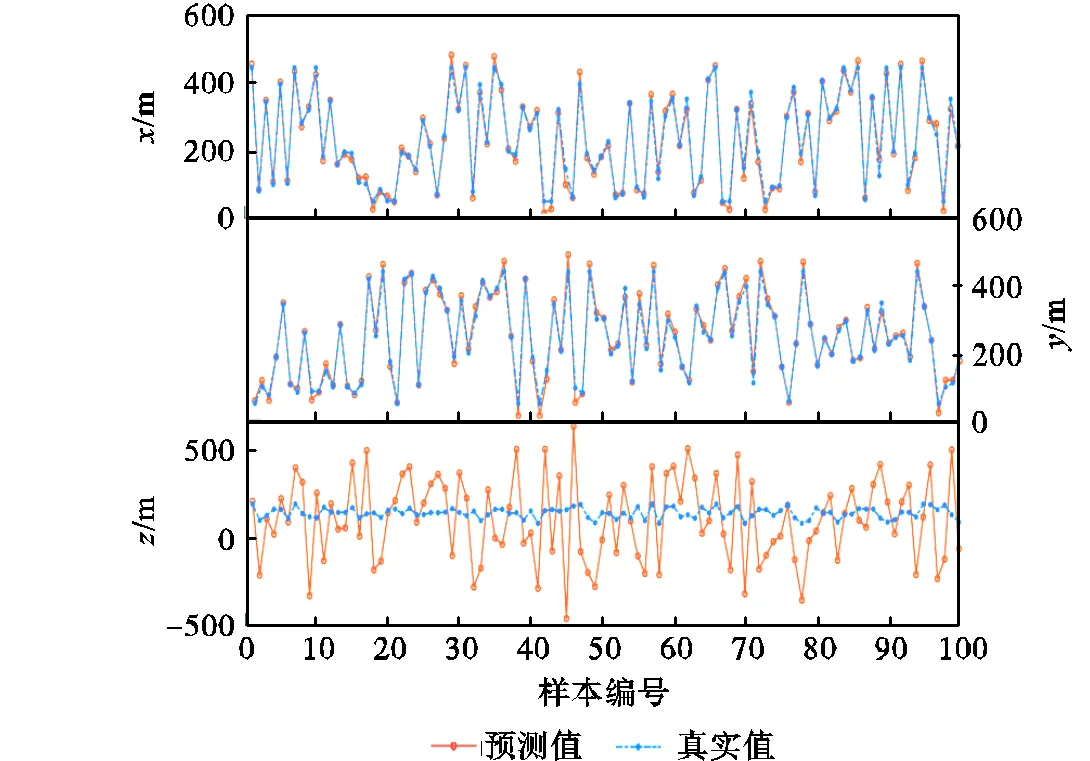
图10 有干扰下优化随机森林模型测试结果

3 结 语

本研究针对复杂海洋环境中定位精度差的问题，提出了基于随机森林模型的高精度水下声学定位预测模型，并对其预测结果进行了分析．实验数据表明，与传统的多点空间定位模型相比，基于随机森林回归的位置估计模型显著提升了定位性能．即使在信号干扰的情况下，该模型仍能准确预测水下声学目标的位置，展现出强大的抗干扰能力．此外，该模型能够实时处理海基站采集的高维数据，无需进行特征选择，为高效水下声学目标定位的工程应用提供了新的思路和可能性．

［1］Zhou S S，Hu X G，Liu L，et al. Status of satellite orbit determination and time synchronization technology for global navigation satellite systems[J]. Chinese Astronomy and Astrophysics，2019，43(4)：479-492.

［2］Li B，Ge H，Ge M，et al. LEO enhanced global navigation satellite system(LeGNSS)for real-time precise positioning services[J]. Advances in Space Research，2019，63(1)：73-93.

［3］张志伟，孙 翱，张 旭，等. 一种海上落点声学测量基站优化布设方法[J]. 计算机仿真，2020，37(11)：10-14，38.

Zhang Zhiwei，Sun Ao，Zhang Xu，et al. An optimal layout method of acoustic measurement base stations for offshore landing points[J]. Computer Simulation，2020，37(11)：10-14，38(in Chinese).

［4］郝建录，历 昌. 一种用于海上打圆桩过程监测的新型测量方法[J]. 海洋测绘，2018，38(5)：59-62.

Hao Jianlu，Li Chang. A new measurement method for monitoring the process of offshore round pile driving[J]. Ocean Surveying and Mapping，2018，38(5)：59-62(in Chinese).

［5］张 旭，孙 翱，韩 旭，等. 水下垂向运动目标的海底多基站声定位方法及精度分析[J]. 声学学报，2019，44(2)：155-169.

Zhang Xu，Sun Ao，Han Xu，et al. Submarine multi-base station acoustic localization method and accuracy analysis of underwater vertical moving targets[J]. Acta Acustica，2019，44(2)：155-169(in Chinese).

［6］Zheng S，Duan G，Xia B. Underwater acoustic positioning based on valley-chirality locked beam of sonic system[J]. International Journal of Mechanical Sci-ences，2020，174：105463.

［7］Tanaka H K M. Muometric positioning system(μPS)with cosmic muons as a new underwater and underground positioning technique[J]. Scientific Reports，2020，10(1)：1-9.

［8］Huang B，Xie L，Yang Z. TDOA-based source localization with distance-dependent noises[J]. IEEE Transactions on Wireless Communications，2015，14(1)：468-480.

［9］周 成，黄高明，单鸿昌，等. 基于最大似然估计的TDOA/FDOA无源定位偏差补偿算法[J]. 航空学报，2015，36(3)：979-986.

Zhou Cheng，Huang Gaoming，Shan Hongchang，et al. TDOA/FDOA passive positioning bias compensation algorithm based on maximum likelihood estimation[J]. Journal of Aeronautics and Astronautics，2015，36(3)：979-986(in Chinese).

［10］Zheng S J，Duan G J，Xia B Z. Underwater acoustic positioning based on valley-chirality locked beam of sonic system[J]. International Journal of Mechanical Sciences，2020，174：105463.

［11］Rodriguez-Galiano V，Sanchez-Castillo M，Chica-Olmo M，et al. Machine learning predictive models for mineral prospectivity：An evaluation of neural networks，random forest，regression trees and support vector machines[J]. Ore Geology Reviews，2015，71：804-818.

［12］Li Y，Zou C F，Berecibar M，et al. Random forest regression for online capacity estimation of lithium-ion batteries[J]. Applied Energy，2018，232：197-210.

［13］Wang L A，Zhou X D，Zhu X K，et al. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data[J]. The Crop Journal，2016，4(3)：212-219.

［14］王志勇，张梦悦，于亚冉，等. 一种融合纹理特征与NDVI的随机森林海冰精细分类方法[J]. 海洋学报，2021，43(10)：149-156.

Wang Zhiyong，Zhang Mengyue，Yu Yaran，et al. A fine classification method for sea ice based on random forest combining texture feature and NDVI[J]. Haiyang Xuebao，2021，43(10)：149-156(in Chinese).

［15］王 妍，王若谷，魏克颖，等. 基于随机森林的致密储层分类——以延安气田东部盒8段为例[J]. 西安石油大学学报(自然科学版)，2021，36(6)：1-8.

Wang Yan，Wang Ruogu，Wei Keying，et al. Classification of tight reservoirs based on random forest algorithm：A case study of He 8 member in east of Yan’an Gasfield[J]. Journal of Xi’an Shiyou University(Natural Science Edition)，2021，36(6)：1-8(in Chinese).

［16］马丽英，张洪杰，罗天洪，等. 基于LMD-CSP和随机森林的运动想象脑电信号分类[J]. 传感技术学报，2021，34(9)：1189-1195.

Ma Liying，Zhang Hongjie，Luo Tianhong，et al. Classification of electroencephalographic signals of motor imagery based on LMD-CSP and random forest[J]. Journal of Sensor Technology，2021，34(9)：1189-1195(in Chinese).

［17］Chen M，Ludtke S J. Deep learning-based mixed-dimensional Gaussian mixture model for characterizing variability in cryo-EM[J]. Nature Methods，2021，18(8)：930-936.

［18］Alimisis V，Gennis G，Touloupas K，et al. Gaussian mixture model classifier analog integrated low-power implementation with applications in fault management detection[J]. Microelectronics Journal，2022，126：105510.

［19］Qu X，Xie L. An efficient convex constrained weighted least squares source localization algorithm based on TDOA measurements[J]. Signal Processing，2016，119：142-152.

［20］Hao P Y，Zhan Y L，Wang L，et al. Feature selection of time series MODIS data for early crop classification using random forest：A case study in Kansas，USA[J]. Remote Sensing，2015，7(5)：5347-5369.

［21］Liu Z，Xu T，Zhou J，et al. Application of stable isotopic and elemental composition combined with random forest algorithm for the botanical classification of Chinese honey[J]. Journal of Food Composition and Analysis，2022，110：104565.

［22］Cheng X，Shu H，Liang Q，et al. Silent positioning in underwater acoustic sensor networks[J]. IEEE Transactions on Vehicular Technology，2008，57(3)：1756-1766.

［23］Han Y F，Zheng C E，Sun D J. Signal design for underwater acoustic positioning systems based on orthogonal waveforms[J]. Ocean Engineering，2016，117：15-21.

［24］Sun D J，Li H P，Zheng C E，et al. Sound velocity correction based on effective sound velocity for underwater acoustic positioning systems[J]. Applied Acoustics，2019，151：55-62.

［25］Aziz El-Banna A A，Wu K，ElHalawany B M. Application of neural networks for dynamic modeling of an environmental-aware underwater acoustic positioning system using seawater physical properties[J]. IEEE Geoscience and Remote Sensing Letters，2020，19：1501505.

Research on Underwater Acoustic Positioning Model of Marine Base Station Based on Optimized Random Forest

Xu Jian1，Jin Kangkang1，Li Zhongzheng2，Wang Lan1，Zhang Zhaoyi1，Liu Yi1

(1. School of Marine Science and Technology，Tianjin University，Tianjin 300072，China；2. Naval Academy，Tianjin 300061，China)

The ocean acoustic target detection technology offers unique advantages in the development of marine resources，protection of marine life，regional marine ecological monitoring，and military applications. However，the performance of receiving sensors is often compromised by external interference sources，leading to decreased positioning accuracy. To address this issue，this paper proposes an optimized random forest-based underwater acoustic positioning model for marine base stations to improve the positioning accuracy. First，data preprocessing is performed on the collected raw signals. For data acquired without interference，unnecessary samples，including missing，abnormal，identical，or similar data，are removed. For data acquired with interference，abnormal cases are identified，and the data from the base stations causing interference is eliminated. Subsequently，principal component analysis (PCA) is used for dimensionality reduction，and the synthesized features are used as inputs for Gaussian mixture clustering. Furthermore，the optimal hyperparameters are determined through a combination of grid search，cross-validation，and mixture coefficients. Then，an underwater acoustic positioning model is established using optimized random forest，and the estimation effect is compared with the multi-base spatial positioning model. Experimental results demonstrate that the root mean square errors(RMSEs) of the three-dimensional positioning of the multi-base spatial positioning model are 5.648 m and 26.264 m respectively under the condition of no interference and interference，while the RMSEs of the model proposed in this paper are 0.232 m and 4.354 m respectively. The proposed method significantly improves the positioning accuracy of the target and exhibits strong generalization capabilities. Specifically，the estimated RMSEs along the，，anddirections with no interference are 0.122m，0.099m，and 0.171m，respectively，while the estimated RMSEs along the，，anddirections with interference are 1.715m，1.691m，and 3.627m，respectively. In particular，the largest positioning error occurs in thedirection，which is consistent with the actual situation. These results validate the effectiveness of the proposed method，providing new insights for high-precision positioning of underwater moving targets and the design of positioning navigation systems.

underwater acoustic positioning；multi-base station；time difference of arrival(TDOA)；optimized random forest；Gaussian mixture clustering

the National Natural Science Foundation of China(No.41706106，No.41702307)，the National Key Research and Development Program of China(No.2016YFC1401203).

10.11784/tdxbz202209037

P229

A

0493-2137(2023)12-1235-09

2022-09-30；

2023-01-31.

徐 剑（1984—  ），男，博士，副教授.Email：m_bigm@tju.edu.cn

徐 剑，jian.xu@tju.edu.cn.

国家自然科学基金资助项目(41706106，41702307)；国家重点研发计划资助项目(2016YFC1401203).

(责任编辑：田 军)