基于环境影响的城轨设备预防性维修方法研究

2023-11-10黎家靖

铁道标准设计 2023年11期

黎家靖，张宁

(1.东南大学智能运输系统研究中心,南京 210018; 2.中铁第四勘察设计院集团有限公司,武汉 430063)

引言

城轨设备数量的不断增加对设备日常维修维护提出了更高要求,科学合理的维修计划能避免设备过维修或欠维修,提高设备可靠性。有学者在设备可靠性及维修维护方面开展了相关研究,文献[1-3]分别对地铁车辆、铁路四电系统、地铁站台门系统进行可靠性状态评估;文献[4]基于RCM理论对轨道车辆转向架系统进行维修决策;文献[5-9]建立基于可靠度约束的城轨设备预防性维修周期优化模型;文献[10]基于生存分析和可靠性理论确定动车组维修时间间隔;文献[11]提出动车组设备的多目标预防性维护间隔确定方法;文献[12-13]构建了地铁列车设备的不完全预防性维修模型;文献[14]引入两级非完美维修,基于混合故障率演化模型构建动车组设备预防性维修策略;文献[15]基于延迟时间理论建立地铁车辆子系统多级维修计划模型及系统级别的成组维修优化模型;文献[16-18]基于机会维修策略构建多部件机会成组维修模型,最终实现列车设备多部件联合维修。

但以上研究在计算预防性维修周期时缺乏考虑外部环境因素对设备可靠性的影响,基于此,构建一种基于环境影响的威布尔比例故障率模型以准确描述城轨设备可靠性变化情况,使用极大似然法和粒子群算法进行模型参数寻优。考虑设备经历预防性维修后的“修复非新”特性,引入役龄回退因子和故障率递增因子以表示预防性维修前后设备故障率变化情况。并以此为基础,基于设备最低可靠度阈值构建预防性维修周期模型确定设备预防性维修周期的大小,通过剩余寿命函数公式预测设备剩余寿命。相关研究结果可为城轨设备的维修维护决策提供一定参考依据。

1 城轨设备故障规律分析

城轨设备故障通常具备一定的客观变化规律,一般而言,在设备全生命周期中,设备性能或状态会随着设备服役时间的增加而逐渐降低[19]。设备性能退化过程如图1所示,其中P点为故障萌发点,F点为功能故障点,位于P点和F点之间的点为潜在故障点。P点表示设备性能开始劣化,通常没有明显征兆;F点表示设备丧失规定功能,发生功能性故障;所有潜在故障点均有可能发生故障,且通常带有明显征兆。对城轨设备而言,可通过获取设备在功能故障点之前的状态参数来评估设备状态,进而提前采取预防性维修活动,避免设备发生故障。

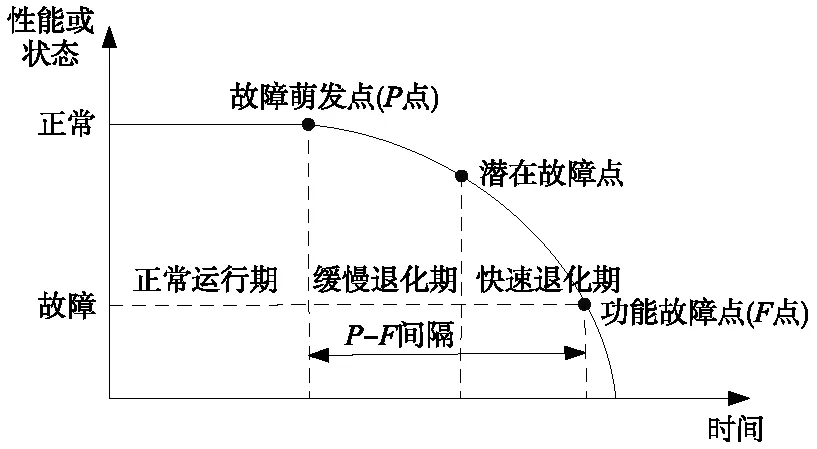
图1 设备性能退化过程

故障率可以很好地反映设备故障变化规律,大多数城轨设备的故障率变化曲线通常符合“浴盆曲线”[20],设备依次经历早期故障、偶发故障以及耗损故障3个时期,如图2所示。在早期故障期,由于设备刚投入使用需进行磨合等缘故导致设备初始故障率较高,但随着磨合时间的增加,设备故障率会快速下降;偶发故障期的设备故障率通常保持恒定,设备故障率低且波动幅度小,材料缺陷、使用不当、运行环境劣化等因素是造成设备偶发故障的主要原因;耗损故障期是设备的运行后期,这一阶段设备磨损、耗损、老化等问题严重,设备性能迅速下降,因此该阶段设备故障率通常会急速增加。显然,偶发故障期是设备的最佳状态期,可通过合适的维修维护活动延长偶发故障期的长度,使设备长期运行在良好平稳的工作状态下。

图2 设备故障浴盆曲线

2 基于环境影响的威布尔比例故障率模型

城轨设备的故障原因包括设备质量、维修水平、服役年限、外部环境等多个方面,其中外部环境因素对设备运行状态的影响不容忽视,有学者指出,运行环境不同,设备的故障次数、故障频率均有所不同[21]。以往研究大多基于设备历史故障失效数据直接拟合得到可靠性函数,未考虑外部环境因素对城轨设备可靠性的影响。因此,本节在传统威布尔分布的基础上引入比例故障率模型,构建基于环境影响的威布尔比例故障率模型以准确描述考虑设备外部环境因素条件下的可靠性变化情况,并为后续城轨设备预防性维修研究打下基础。

2.1 威布尔分布

威布尔分布是分析设备可靠性变化情况的常用模型之一,其能准确描述处于不同故障阶段的设备失效过程。若设备故障失效数据符合威布尔分布,其故障率为

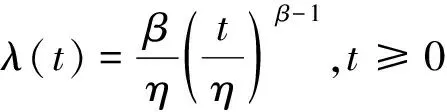
(1)

式中,t为设备的运行时间;η、β分别为尺度、形状参数,且η>0、β>0。当0<β<1时,故障率曲线呈下降趋势,对应于浴盆曲线早期故障期;当β=1时,故障率曲线近似为一条水平线,对应于浴盆曲线偶发故障期;当β>1时,故障率曲线呈上升趋势,对应于浴盆曲线耗损故障期。

2.2 威布尔比例故障率模型构建

城轨设备的故障分布特征通常符合威布尔分布,其运行状态受设备所处位置的外部环境影响,包括温度、湿度、磁场、辐射等。考虑外部环境因素对城轨设备可靠性的影响,在威布尔分布的基础上通过引入协变量的形式将设备故障率与影响设备状态的外部环境因素建立联系,构建基于环境影响的城轨设备威布尔比例故障率模型(Weibull Proportional Hazards Model,WPHM模型)。

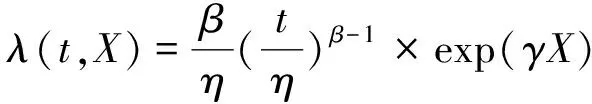
(2)

式中,λ(t,X)为设备故障率;X为影响城轨设备运行状态的外部环境因素,X=(x1,x2,…,xp),p为环境影响因素的个数;γ为环境影响因素的系数,γ=(γ1,γ2,…,γp)。

由此,可得出设备的可靠度函数R(t,X)、故障概率密度函数f(t,X)如下

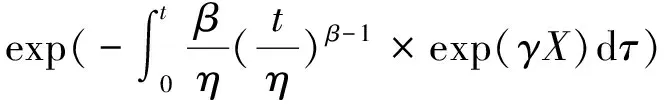
(3)

(4)

2.3 模型参数估计

为确定2.2节中威布尔比例故障率模型的η、β和γ=(γ1,γ2,…,γp),一共p+2个未知参数的值,基于极大似然法(Maximum Likelihood Estimate,MLE)和粒子群算法(Particle Swarm Optimization,PSO)对模型进行参数优化估计。

极大似然法的核心是构造对数似然函数,再对其求偏导数以得到未知参数估计值,但一般而言对数似然函数包含指数、积分等运算,直接求导存在计算复杂、计算量大等问题。通过分析极大似然法参数求解过程可知,当其对数似然函数取到最大值时便可得到未知参数的极大似然估计值。基于此,考虑直接对对数似然函数求导存在一定困难,在极大似然法的基础上使用PSO算法对未知参数η、β和γ进行参数优化估计,以对数似然函数作为PSO算法的适应度函数对各粒子进行迭代更新,适应度函数的值越大,PSO算法寻优得到的参数估计值越接近参数真实值。

本节基于环境影响的城轨设备威布尔比例故障率模型构建及求解的具体流程如图3所示。

图3 威布尔比例故障率模型构建及求解流程

3 城轨设备预防性维修方法

以第2节为基础,引入役龄回退因子和故障率递增因子对城轨设备退化过程进行建模,以可靠度为约束确定设备预防性维修周期,并构建剩余寿命函数预测设备剩余寿命,以此为开展城轨设备预防性维修活动提供参考依据。

3.1 设备退化过程建模

由图1可知,城轨设备的性能会随其服役时间的增加而逐渐退化,当设备性能退化至一定程度时需对其采取必要的维修维护活动。在城轨设备实际维修中,预防性维修虽然能改善设备性能,提高设备可靠度,但却难以使设备性能完全恢复如新,因此,实际的预防性维修活动在本质上是一种不完全维修方式。

为准确描述城轨设备经历不完全预防性维修后的“修复非新”情况,引入役龄回退因子和故障率递增因子对设备退化过程进行建模。役龄回退因子决定预防性维修后的设备役龄回退时间,役龄回退因子的值越小,设备役龄回退时间越多,表示设备维修效果越好;故障率递增因子决定预防性维修后的设备故障率变化速率,故障率递增因子的值越大,设备故障率递增速率越大,表示设备性能退化越快。

图4为设备实际役龄时序关系,其中,第k次预防性维修前后的设备实际役龄如下

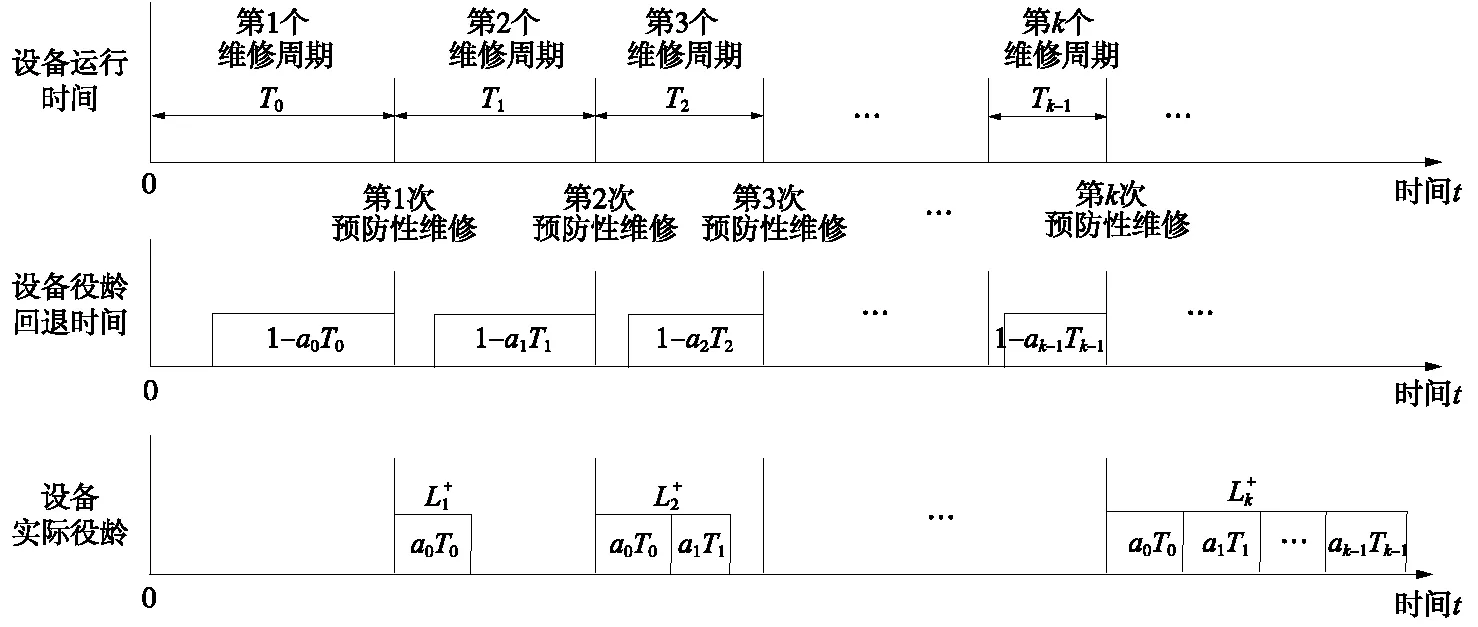
图4 设备实际役龄时序关系

(5)

基于役龄回退因子与故障率递增因子的设备故障率变化曲线如图5所示,其中设备第k次预防性维修后的故障率λk(t,X)公式如下

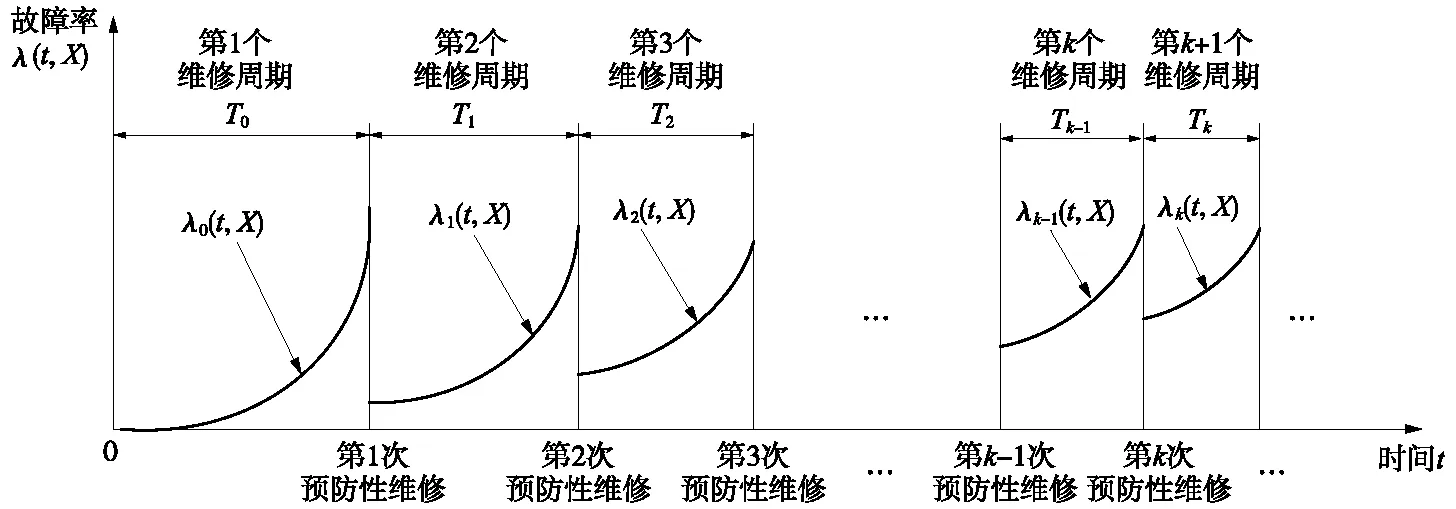
图5 设备故障率变化曲线

λk(t,X)=bk-1×λk-1(t+ak-1Tk-1,X)

(6)

假设设备的初始基准故障率函数为λ0(t,X),结合2.2节中的WPHM模型,得到故障率递推关系如下

λ1(t,X)=b0λ0(t+a0T0,X)=

λ2(t,X)=b1λ1(t+a1T1,X)=b0b1λ0(t+a0T0+

……

λk(t,X)=bk-1λk-1(t+ak-1Tk-1,X)=……=

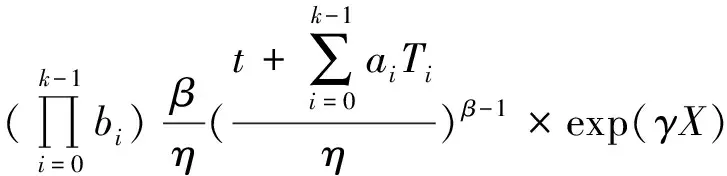
(7)

3.2 预防性维修周期确定

城轨设备在运行过程中其可靠度R(t,X)≥最低可靠度阈值α,即应满足以下要求

R(t,X)≥α

(8)

式(8)表明,当城轨设备可靠度下降至最低可靠度阈值,应对其进行预防性维修。若城轨设备的故障分布特征满足威布尔分布,结合式(3)、式(7)、式(8)可构建以下城轨设备预防性维修周期求解方程。

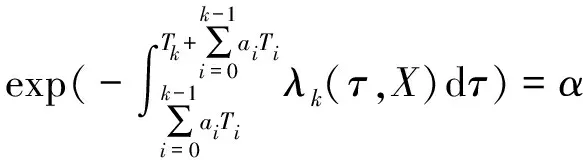
(9)

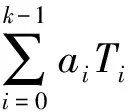
3.3 剩余寿命预测

计算城轨设备在时刻t的剩余寿命期望值,并将该值作为剩余寿命的预测值,具体如下

(10)

式中,RUL(t,X)为设备在时刻t的剩余寿命。

4 实例分析

本小节以地铁屏蔽门设备为研究对象,验证基于环境影响的城轨设备威布尔比例故障率模型及预防性维修方法的正确性。地铁屏蔽门主要由门体系统、控制与监视系统、电源系统以及其他系统四部分组成[22],一般设置在地铁站台边缘以隔离列车和站台候车区的乘客,其必须具备高可靠性和低故障率以保证乘客出行安全,通常屏蔽门的故障率应小于0.8次/万次[23]。因此,选择屏蔽门设备为研究对象具有一定的代表性和研究意义。

4.1 设备故障数据及分析

以某地铁车站的屏蔽门实际故障数据为例进行分析,该车站为地上三层高架车站,其屏蔽门位于三楼的高架站台,设备运行状态会受到外部环境因素的影响,以该车站的屏蔽门故障数据进行实例分析具有一定参考价值。故障数据统计范围为2015年11月1日至2018年10月31日,具体如表1所示。

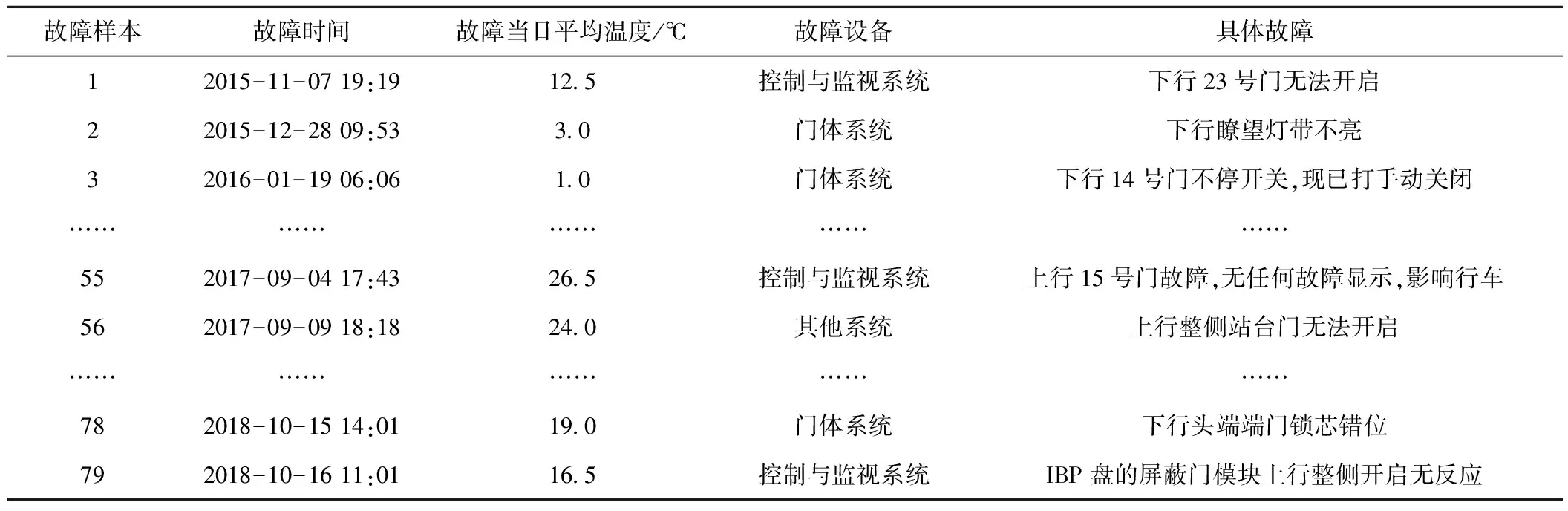
表1 屏蔽门设备实际故障数据

由于该车站的屏蔽门设备位于室外,其受到外部环境因素的影响较大,设备在不同季节的故障情况和故障次数具有较大差异。图6为该屏蔽门设备各个季节的故障次数统计,由图6可知,设备夏季、冬季故障次数最多,且远高于春季和秋季。温度是表征季节差异的主要因素,不同的季节温度明显不同,该地铁车站所在市的春夏秋冬4个季节的平均气温分别为17,29,19,5 ℃。显然,夏季温度高,冬季温度低,温度过高或过低对设备运行状态影响较大,进而导致设备故障次数增加;春季、秋季温度刚好合适且二者平均温度数值相差不大,所以这两个季节设备故障次数最少且故障次数较为接近。因此,温度是造成该屏蔽门设备在不同季节故障率变化显著的重要原因,在对其进行预防性维修研究时应考虑温度因素对设备可靠性的影响。

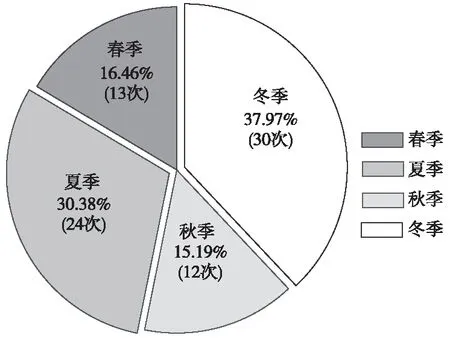
图6 某车站屏蔽门设备各季节故障次数统计

4.2 模型参数估计

以设备故障当日平均温度表征外部环境因素对设备状态的影响,即选取温度为协变量,协变量个数为1个。则考虑环境影响的城轨设备威布尔比例故障率模型为

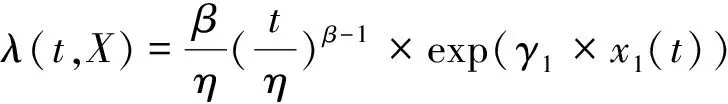
(11)

式中,x1(t)为设备t时刻的当日平均温度。

模型的对数似然函数lnL(η,β,γ1)如下

exp(γ1×x1(τ))dτ

(12)

将lnL(η,β,γ1)作为优化目标函数并使用粒子群算法对WPHM模型中的未知参数η、β和γ1进行参数优化估计,粒子群数量、迭代周期以及各参数的寻优范围设置如表2所示。代入表1的屏蔽门设备故障数据,得到PSO算法参数优化估计迭代结果,如图7所示,其中模型适应度值随着迭代轮数的增加而不断增加,并最终趋于收敛,因此,PSO算法对WPHM模型的参数估计具有良好效果。

表2 PSO算法相关参数设置

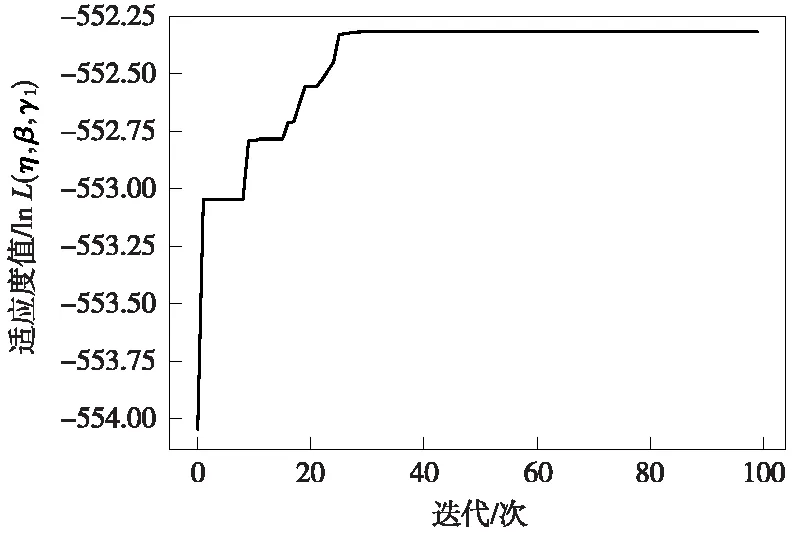
图7 PSO算法迭代结果

传统威布尔分布模型与WPHM模型的参数估计结果如表3所示。由表3可知,两个模型的形状参数β估计值相差不大,反映出模型参数估计的一致性和准确性,此外,由于β值的大小决定了设备故障率曲线的形状,表3中两个模型的β值均大于1,因此该屏蔽门设备正处于耗损故障期。以平均绝对百分比误差(简称“MAPE”)作为评估指标对各模型进行误差对比分析,传统威布尔分布模型的MAPE误差为0.163 5,考虑了外部环境影响的WPHM模型的MAPE误差0.093 3,MAPE误差降低了约43%,说明考虑环境影响的WPHM模型能有效表示外部环境因素对城轨设备状态的影响,降低模型拟合误差,从而更加准确地描述设备的可靠性变化情况。

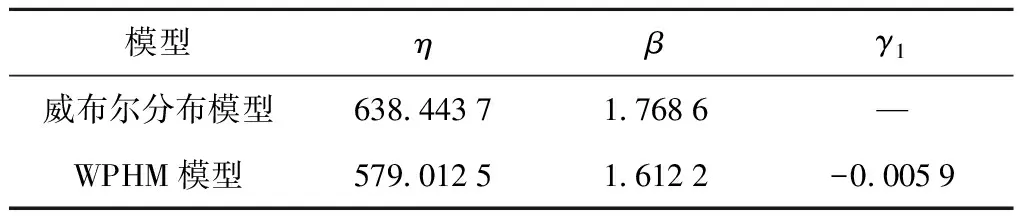
表3 各模型参数估计结果

4.3 预防性维修仿真

4.3.1 设备故障率曲线

根据表3参数可得到该屏蔽门设备的故障率函数λ(t,X)如下

exp(-0.005 9×x1(t))

(13)

将各时刻的当日平均温度数据代入上式得到该屏蔽门设备的故障率曲线,如图8所示。从故障率曲线可以看出,受到外部环境因素影响,故障率曲线存在一定波动,但总体来说,随着设备运行时间增加,故障率曲线稳态逐步上升,与浴盆曲线的故障率变化规律一致。

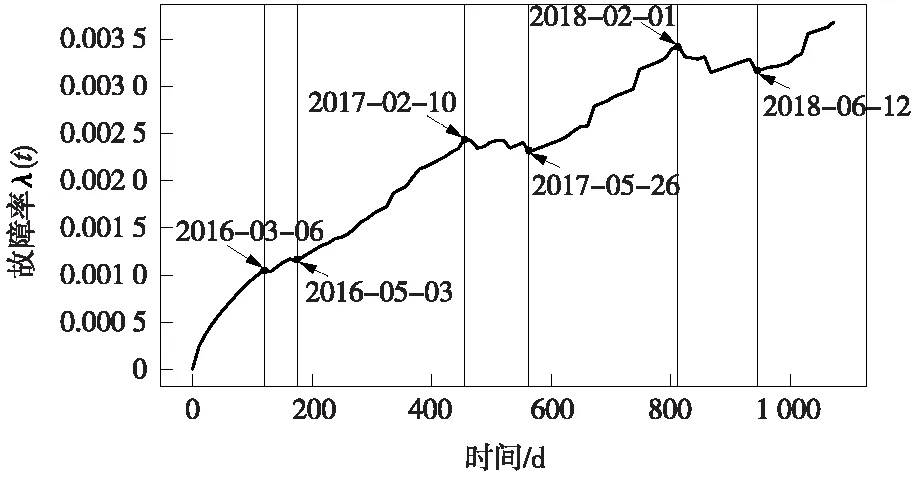
图8 屏蔽门设备故障率曲线

该屏蔽门设备故障率曲线中有3处上下波动幅度较大的地方,且这3处地方的起始时间均在每年的2、3月份,此时间点刚好是每年冬季与春季的过渡时间段,春季温度回暖,设备运行的外部环境条件变好,其故障率会有所降低,但由于设备服役时间在不断增加,其故障率曲线便出现了上下波动的现象。由于受到全球变暖影响,该屏蔽门设备所在市的每年春季均较前一年提前到来,导致设备运行的外部环境温度回暖提前,因此,这3处上下波动的起始时间较前一年均有所提前。

此外,这3处上下波动地方的持续时间间隔依次逐渐增大,间隔时间分别约为55,108,133 d,时间间隔逐渐增大的原因在于设备服役时间和外部环境因素对设备状态的影响比重在不断变化造成的。一开始设备刚投入使用不久,此时设备服役时间短,设备状态完好,外部环境因素对设备状态的影响较小,因此设备故障率曲线发生第1次上下波动时,持续时间较短且设备在刚开始运行的一段时间内其故障率稳步上升;随着设备服役时间增加,相较于刚投入使用时设备状态有所下降,此时,设备服役时间对设备状态的影响比重减小,外部环境因素对设备状态的影响比重增大,因此,第2、3次上下波动的持续时间较长,且这两次波动的时间间隔均在120 d左右,刚好对应春季结束、夏季开始的时间点,在夏季开始后设备受到外界环境温度升高的影响其故障率持续上升。

4.3.2 设备预防性维修周期

以式(13)作为该屏蔽门设备初始的基准故障率函数,取设备预防性维修次数为20次,设备最低可靠度阈值设置为0.9,由此得到基于可靠度约束的设备历次预防性维修的周期大小,计算结果如图9所示。图9中屏蔽门设备预防性维修周期的大小整体上呈现出逐渐减小的态势,在设备运行前期,设备服役时间是其故障率变化的主导因素,因此这一阶段设备预防性维修周期逐渐减小;设备运行一段时间后,随着屏蔽门设备的服役时间增加,设备服役时间对设备状态的影响比重减小,外部环境因素成为影响设备故障率变化的主要因素,因此在这一阶段设备预防性维修周期大小会出现小幅度上下波动的情况。此外,该屏蔽门设备在运行后期的预防性维修周期数值远小于其在运行前期的预防性维修周期数值,且设备在运行后期的维修周期大小基本趋于稳定不变,这是由于屏蔽门设备在运行后期耗损、老化严重,因此,在设备运行后期需要频繁进行预防性维修活动以保证其可靠度始终维持在一定水平之上。

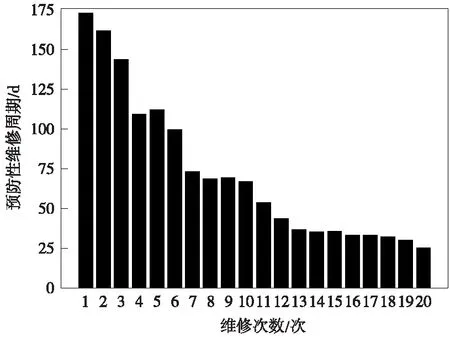
图9 屏蔽门设备历次预防性维修周期计算结果

4.3.3 设备剩余寿命

基于役龄回退因子和历次预防性维修周期计算结果,得到该屏蔽门设备历次预防性维修后的实际役龄数据,如表4所示。

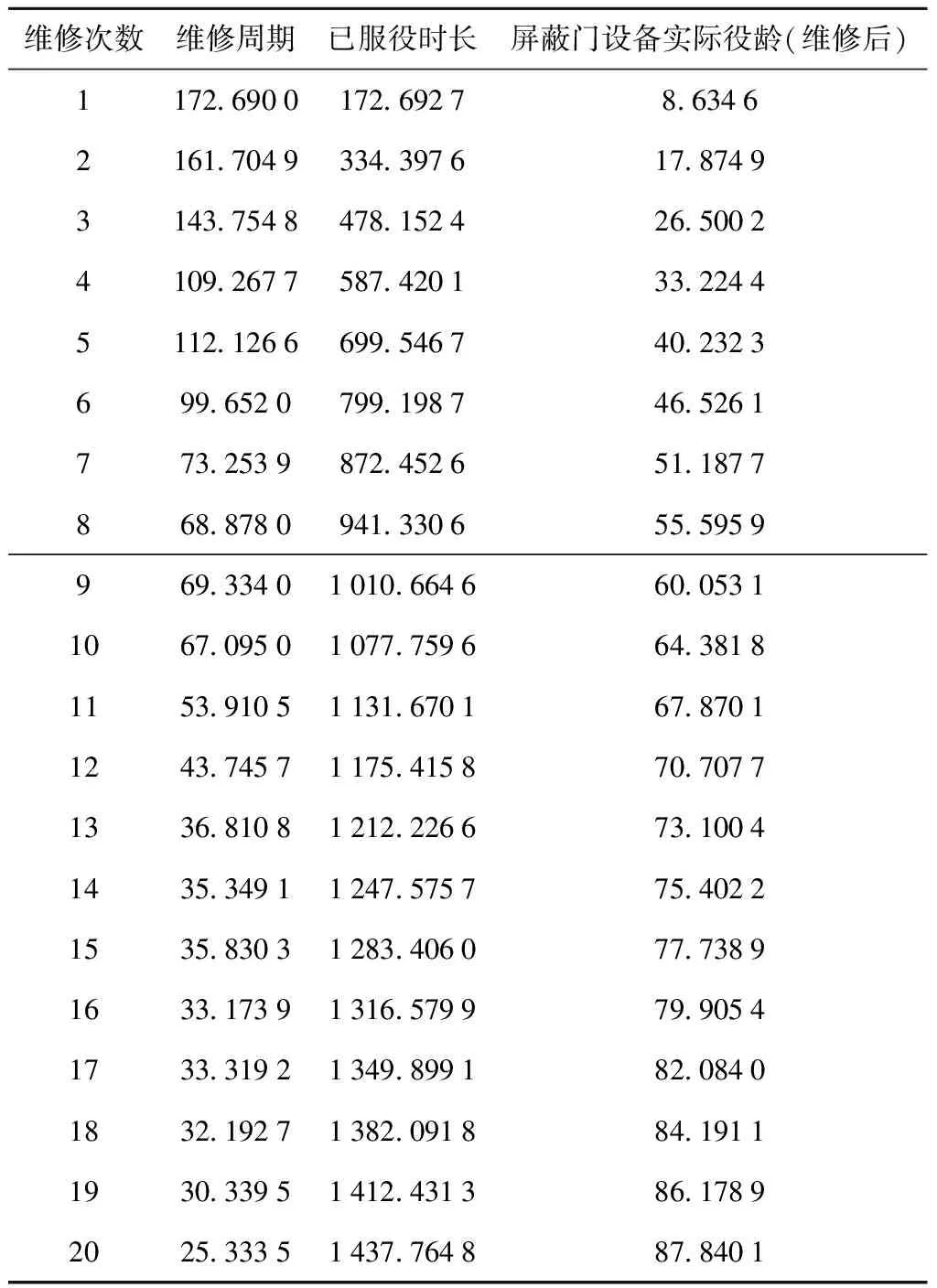
表4 历次预防性维修后屏蔽门设备实际役龄 d

将表4最后一列数据代入式(10)中便可得到该屏蔽门设备在历次预防性维修后的剩余寿命,如图10所示。由图10可知,随着设备预防性维修次数和服役时间增加,设备实际役龄逐渐增加,设备的剩余寿命在总体趋势上也随之减小,满足客观变化规律。由于受到外部环境因素的影响,设备剩余寿命并未呈现严格单调递减,设备剩余寿命函数曲线在设备运行前期下降幅度较快,在设备运行后期下降幅度减缓且出现上下波动现象,说明设备运行后期外界环境因素对设备状态的影响大于运行前期,与图8、图9的分析结果一致。