浅埋大直径盾构隧道开挖面局部破坏的被动稳定性研究

刘 庆，崔秀丽，秦鹏飞

(1.郑州工业应用技术学院,河南新郑 451100; 2.郑州铁路职业技术学院,郑州 450010)

引言

近年来,在地下空间利用需求和盾构技术进步的推动下,城市地铁隧道建设的步伐日益加快。盾构法具有对周围环境扰动小且施工快速、安全等优势,在我国城市地铁建造中广泛运用。在盾构掘进过程中,通过控制仓内(土仓或泥水仓)土压支撑刀盘外部的土水压力,从而维持盾构隧道开挖面的稳定。若仓内土压不足可能导致开挖面倒塌引起主动破坏;若仓内土压过高会造成地面隆起发生开挖面被动破坏[1]。因此,支护压力的合理设置成为确保开挖面稳定的关键。

近年来,针对盾构隧道开挖面的主动破坏研究已屡见不鲜,而与开挖面被动破坏有关的研究则鲜有报道。通过现场实测及数值模拟表明,浅埋盾构隧道掘进过程中,开挖面发生被动破坏的可能性更大[2]。在实际工程中,隧道的覆土厚度一般为盾构直径的1.0～1.5倍以上。然而,随着我国城市化进程加快,大直径盾构隧道工程已屡见不鲜,且为提高地下空间利用率,大直径地铁隧道的设计埋深在逐渐减小,覆土厚度大多为小于1倍隧道的直径。如上海银都路过江隧道,其直径14.5 m,而覆土厚度仅为10.69 m[3]。对于此类大直径浅埋盾构隧道,开挖面的被动破坏在施工中易产生重大风险,因此,在设计及施工中亟需重视开挖面的稳定性分析。

极限分析法在盾构隧道开挖面稳定性分析中被广泛采用。而极限分析上限法则通过外力功率与系统内部耗散功率的平衡来确定作用在破坏机构上的外部临界载荷。由于上限法将运动学容许破坏机制与外力求解两部分结合,将其应用于盾构隧道开挖面稳定性分析时,可通过构建破坏机制来分析开挖面的稳定,从而确定极限支护压力。LECA和DORMIEUX[4]提出了隧道开挖面的二维圆锥体被动破坏机制,并采用极限分析法求得了极限支护压力的上限解。SOUBRA[5-6]将上述机制改进为多块圆锥体破坏机制,进一步提高了极限支护压力上限解的精度。而MOLLON等[7-8]引入运动学容许原理,提出了盾构隧道开挖面平动和转动的破坏机制。ZHANG等[9]分析了圆形隧道开挖面的主动和被动稳定性,扩展了具有复曲面包络线的连续速度场的破坏机制。闵凡路[10]等认为,大直径盾构隧道开挖面顶部和底部仓内土压与地层土水压力差值非常明显,特别是在浅覆土地层施工时,易导致开挖面发生被动破坏事故。胡艳峰[11]等认为,仓内被动土压的分布情况会导致开挖面的破坏模式更为复杂。DIAS等[12]通过数值模拟发现,浅埋大直径盾构隧道的开挖面易发生局部被动破坏。ANAGNOSTOU和KOVRI[13]对由于支护压力不足而导致的开挖面局部塌陷的现象进行分析,发现这种塌陷发生在开挖面下半部分而不是发生在仰拱处。LI等[14]分析了软黏土中大直径盾构掘进过程的开挖面局部被动破坏,认为在过大的支护压力下,局部被动破坏可能在全面破坏之前发生。王林等[15]提出了一种考虑局部失稳模式的隧道开挖面被动破坏的新机制,该机制由5个圆锥台和作用在圆锥台上的分布力组成。综上所述,浅埋大直径盾构隧道极易发生开挖面的被动破坏,仓内土压的分布模式不仅对破坏模式有影响,而且这种破坏多为局部破坏。然而,上述研究要么只考虑了仓内土压分布的影响,要么只考虑了开挖面局部破坏的影响,将二者同时结合起来开展开挖面被动稳定性分析的研究却很少。

基于极限分析上限法,在考虑仓内土压梯形分布和开挖面局部破坏的前提下,建立一种改进的二维旋转被动破坏机制,提出了大直径盾构隧道开挖面极限支护压力的计算方法。同时,探讨了土体参数和隧道埋深对极限支护压力的影响,并将本文获得的极限支护压力与现有方法进行了比较。最后将该机制运用于某实际工程来验证该上限解的合理性,为今后大直径盾构的安全施工提供一定借鉴。

1 开挖面被动稳定性分析上限解

1.1 支护压力

传统盾构机刀盘直径一般为6～8 m,这种类型的开挖面直径较小,则仓内土压可近似为均匀分布,且合力作用于开挖面中心。然而,大直径盾构机刀盘直径为10～15 m,这种大直径盾构机的仓内土压呈梯形分布,通常以仓内土体的单位重度为速率,沿着开挖面的深度方向线性增加,通常在10～12 kN/m3之间。将盾构隧道直径定义为D,盾构隧道覆土厚度定义为C。假设地下水位位于地表,而地下水位高度到开挖面的距离为H。土体服从Mohr-Coulomb塑性本构模型,并遵循相关联流动法,通常c′为土体有效黏聚力,φ′为土体有效摩擦角,γ′为土体有效重度,γw为水重度,σs为地表超载。大直径盾构隧道开挖面在均质土层中的支护压力分布情况如图1所示。由图1可知,大直径盾构机的仓内土压呈梯形分布,且随着开挖面的深度以土体浮重度γF的速率线性增加,任意深度处开挖面的支护压力可由式(1)、式(2)表示。而开挖面发生局部被动破坏的特征以归一化深度η=DL/D表示,其中,DL为由隧道拱顶至局部破坏特征点的距离。

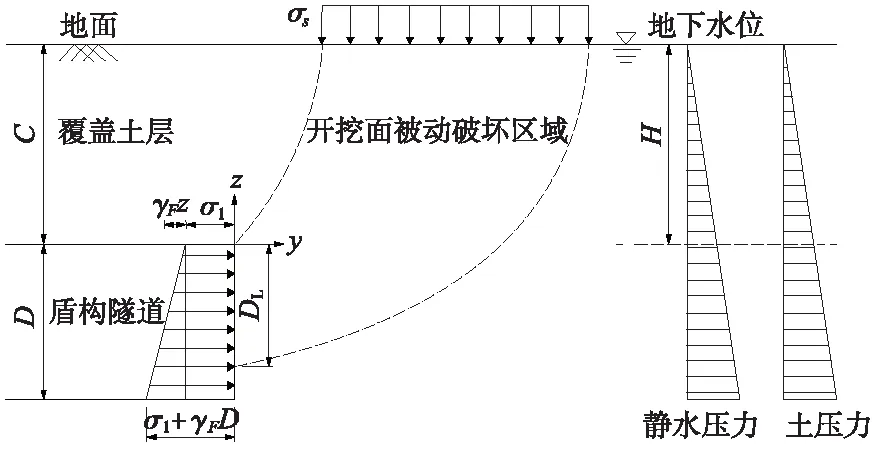
图1 盾构隧道开挖面上的仓内土压分布

σT=σ1+γFz

(1)

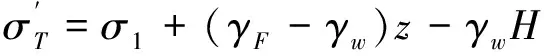
(2)

1.2 破坏机制

极限分析法采用运动学和静力学方法,通过构建土体极限状态下对应破坏机制模型确定土体破坏时对应的临界破坏荷载,是盾构隧道开挖面稳定性分析领域中经典的方法[16]。虽然三维破坏机制模型可以更准确地预测开挖面的极限支护压力,但是许多研究者仍然采用二维理论框架来解决实际问题。在工程设计与施工实践中,应用理论方法快速、简便地计算极限支护压力是非常重要的。因此,开挖面二维破坏机制模型可以为盾构隧道设计和施工提供一个比较理想的手段。

为有效构建开挖面前方土体极限应力状态下的破坏机制模型,提出以下假设:(1)实际工程中的土体为黏性摩擦土(c≠0 kPa,φ≠0°),且服从Mohr-Coulomb塑性本构模型并遵循相关联流动法;(2)土体发生变形后的几何尺寸与变形前的变化相差很小;(3)忽略盾构机刀盘转动引起的摩擦对开挖面稳定性的影响;(4)忽略盾构掘进管片支护对开挖面后方产生的影响;(5)开挖面前方土体均已进入塑性状态[17-18]。

本文对MOLLON等[7-8]提出的破坏机制进行了相应修正,构建开挖面局部被动失稳的破坏机制,如图2所示,开挖面前方土体的破坏区边界即为该破坏模式的形状。为清楚地描述该破坏机制的几何关系,分别定义了两套不同的坐标系。首先以A点为原点,定义一套平面直角坐标系yoz,其次以O点为原点,定义另一套极坐标系(r,β),其中点A坐标为(0,0),点O在yoz坐标系中的坐标为(YO,ZO)。整个破坏机制ABCD在平面内以ω的角速度绕着O点作刚体转动,其中,AB为局部破坏的长度DL,AE为开挖面的直径D,将η定义为局部破坏比,则有AB/AE=DL/D=η,根据几何关系B点在yoz坐标系中的坐标为(0,-ηD)。MOLLON等[7-8]认为整个破坏机制主要由两条对数螺旋线围成,如图2所示,AD和BC分别为两条对数螺旋,AD和BC的方程如式(3)～式(6)所示。

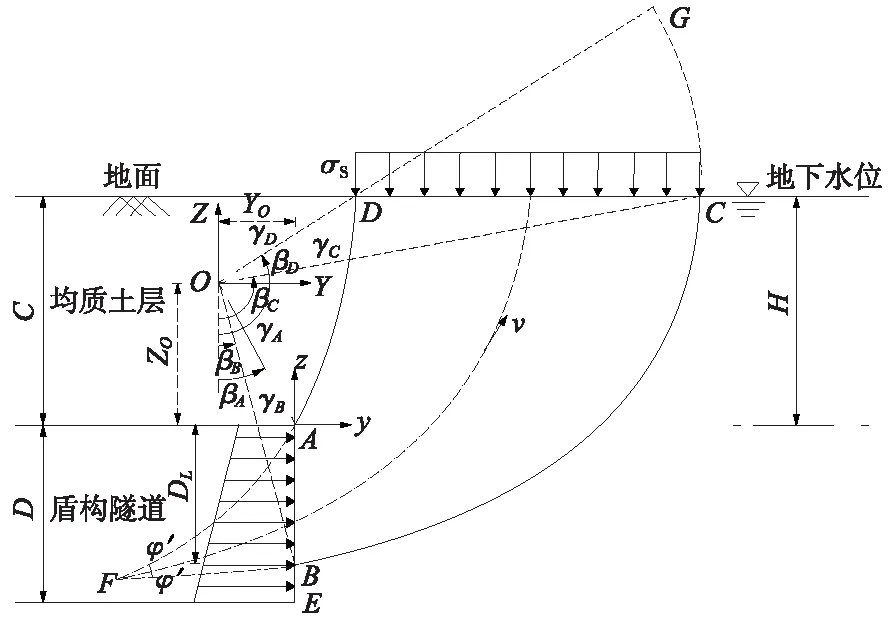
图2 盾构隧道开挖面局部被动破坏机制

AD:r1(β)=rA·e(βA-β)tanφ′

(3)

BC:r2(β)=rB·e(β-βB)tanφ′

(4)

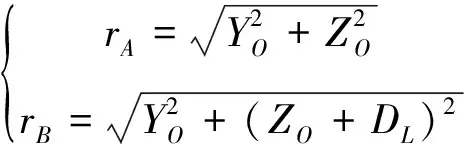
(5)

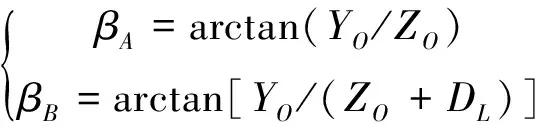
(6)

式中,rA和rB分别为OA和OB的长度,OA和OB与z轴负半轴的夹角为βA和βB,即A和B两点的极坐标可表示为(βA,rA)、(βB,rB)。

由于C和D两点位于地表,且地表在破坏机制中是一条水平直线,于是由几何关系可得式(7)、式(8)。

(7)

C-ZO=rCcos(π-βC)=rDcos(π-βD)

(8)

式中,(βC,rC)和(βD,rD)分别为C和D两点的极坐标。

综上所述,破坏机制ABCD的各项参数βA,rA,βB,rB,βC,rC,βD,rD均可以由式(3)～式(8)通过O点坐标(YO,ZO)表示。当局部破坏比η=1时开挖面发生全局破坏,若仅已知参数YO和ZO无法构建前文假设的局部破坏机制,因此,还需要确定局部破坏比η的值,接下来通过极限分析上限法功能平衡原理来计算参数YO、ZO和η的值。

1.3 上限法求解

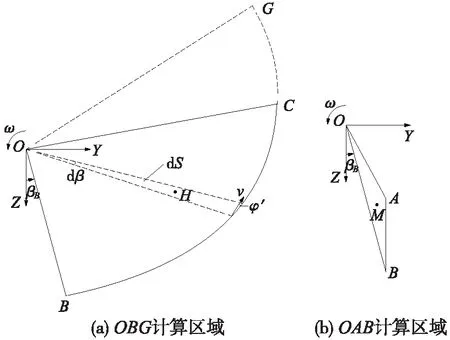
图3 不同计算区域示意

OBG计算区域示意如图3(a)所示,在此区域中选无穷小面积dS,并假定点H为该面积的重心,此时无穷小面积的重力功率如式(9)～式(11)所示。

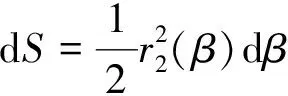
(9)

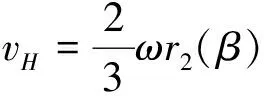
(10)

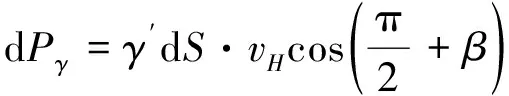
(11)

由图3(a)可知,点G位于点D的延长线上,此时点D的极角即为点G的极角,同时联立(4)(9)(10)(11)四式即可求解OBG中土体重力做功功率,如式(12)～式(14)所示。

(12)

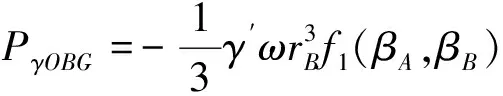
(13)

式中

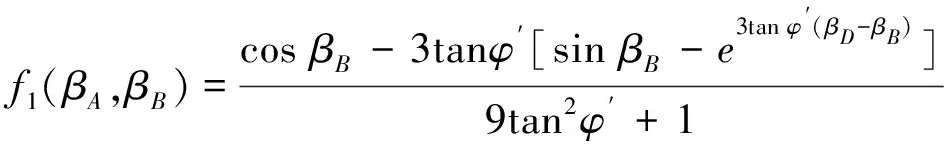
(14)

OAD的重力做功功率也可由上述方法进行求解,如式(15)所示。

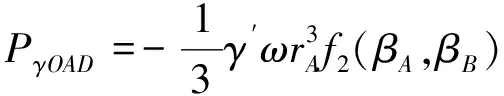
(15)

式中

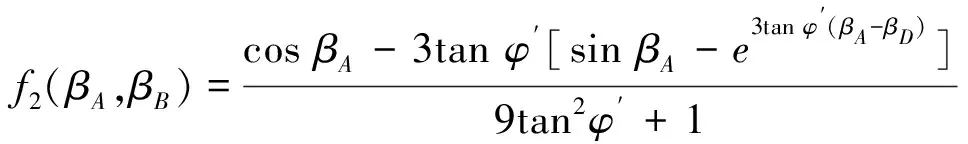
(16)

OAB计算区域示意如图3(b)所示,假定点M为OAB的重心,则点M处线速度可表示为vM=ω·OM。由此可得OAB中土体重力做功功率如式(17)、式(18)所示。

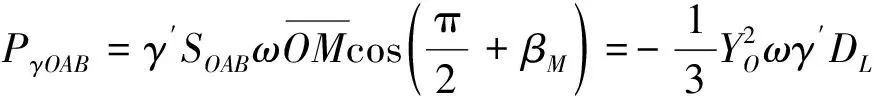
(17)

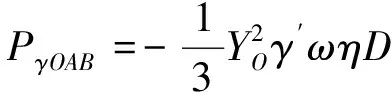
(18)

OCD和OCG中土体重力做功功率如式(19)、式(20)所示。

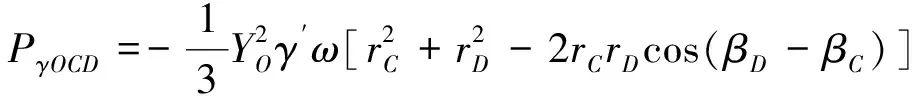
(19)

(20)

式中

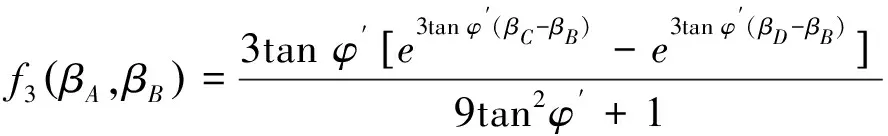
(21)

最终联立(13)(15)(19)(20)四式即可求解土体重力做功的功率Pγ,如式(22)所示。

Pγ=PγOBG-PγOAD-PγOAB-PγOCG+PγOCD

(22)

(23)

式中

(24)

地表超载σs做功的功率PS如式(25)所示。

2(C-ZO)tanφ′]

(25)

整个破坏机制ABCD内部耗散的功率Pv主要产生在速度不连续边界AD和BC上,这两处的耗散功率PvAD和PvBC如式(26)、式(27)所示。

(26)

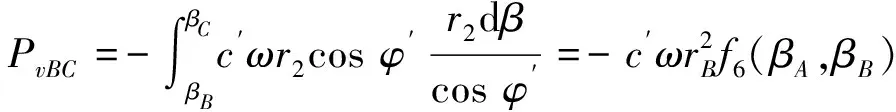
(27)

式中

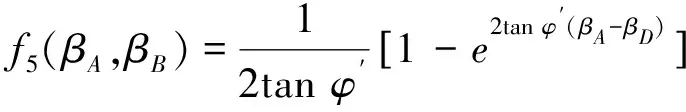
(28)

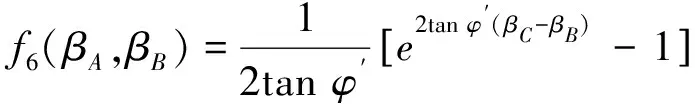
(29)

基于极限分析上限法理论,当整个破坏机制的外部荷载功率Pe等于内部耗散的功率Pv时,如式(30)所示,即可求解开挖面极限支护压力上限解。

Pγ+PT+PS=PvAD+PvBC

(30)

于是联立(22)(23)(25)(26)(27)五式,则开挖面极限支护压力的上限解如式(31)所示。

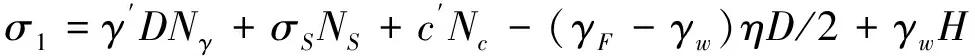
(31)

式中

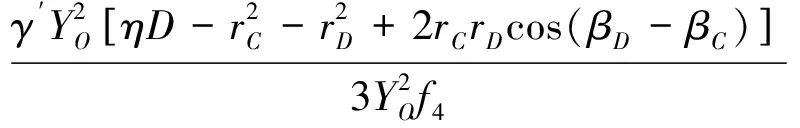
(32)

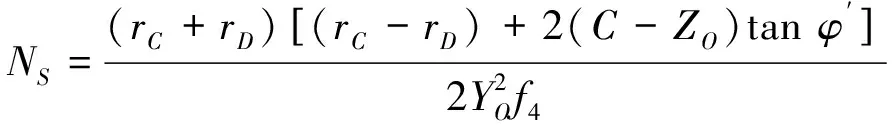
(33)

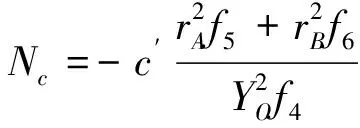
(34)

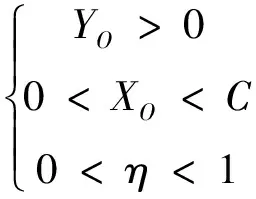
(35)

由式(31)～式(34)可知,本文推导的极限支护压力上限解可由YO、ZO和η三个参数表示,而式(35)即为该上限解的边界条件。由于c′、φ′、γ′、C和D均已知,则σ1是YO、ZO和η的函数,于是采用Matlab约束优化工具箱计算YO、ZO和η的最优值,再将以上最优值参数代入式(31)、式(34)中,所得最小值即为开挖面极限支护压力,其计算程序的流程如图4所示。

由图4可知,先将各项计算参数(c′,φ′,γ′,C,D)代入前文所建立的计算模型中,再假设YO、ZO和η三个参数均为1,通过Matlab程序不断迭代搜索确定σ1的最小值,此时参数YO、ZO和η的最优值即为所得。在盾构掘进过程中,由于土体物理力学参数(c′,φ′,γ′)和隧道设计参数(C,D)是不断变化的,因此,当开挖面发生被动破坏时,其极限支护压力和破坏模式也是不断变化的,但是YO、ZO和η也是随着上述计算参数变化的,基于本文所提出的上限解只要确定了YO、ZO和η三个参数,盾构掘进过程中任意时刻的极限支护压力和破坏模式都可以确定。

2 计算结果分析

2.1 无量纲系数分析

支护压力σ1是变量YO、ZO和η的函数,这3个变量分别决定了破坏区位置和局部破坏的起源。为分析局部破坏比η对极限支护压力的影响情况,以3种不同的埋深比(C/D=0.25,0.50,0.75)为例进行分析。假设土体的单位有效重度为γ′=9.8 kN/m3,地面不存在超载(σS=0 kPa)。为简化计算,假设γF=γw,则在式(31)中有(γF-γw)ηD/2=0。因此,可以认为当γF值很高时,(γF-γw)ηD/2项占据了很大一部分的支护压力。而对于无黏性土(c′=0),式(31)可化简为σ1=γ′DNγ+γwH,所以当γwH为一恒定的值时,σ1的大小完全由Nγ来决定。于是为分析局部破坏比η的影响,表1列出了不同情况η和Nγ值。

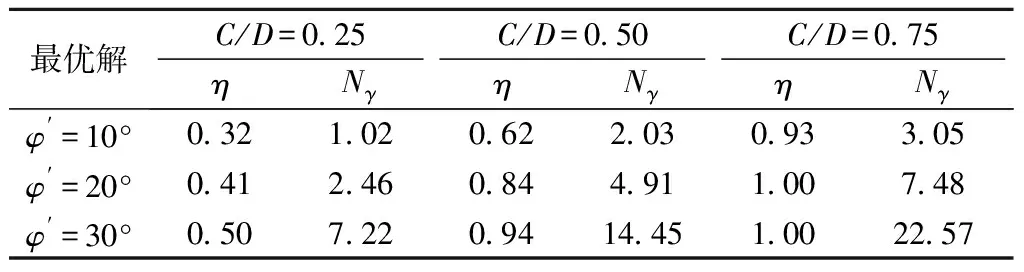
表1 不同φ′值情况下η与Nγ的最优解

由表1可以看出,局部破坏比η是φ′和C/D的函数,η值随φ′和C/D值的增大而增大。若η值增大,表示破坏区域内的土体向盾构隧道仰拱处移动。随着φ′从10°增加至30°,当C/D=0.25时,η从0.32增加至0.50;当C/D=0.50时,η从0.62增大至0.94,表明局部破坏区域从盾构隧道开挖面的下部开始向上发展;特别是当η=0.94时,表明局部破坏区起源于盾构隧道仰拱附近的一个深度内。当C/D=0.75时,局部破坏发生在盾构隧道仰拱处或仰拱附近。φ′和C/D对局部被动破坏模式的影响如图5所示。

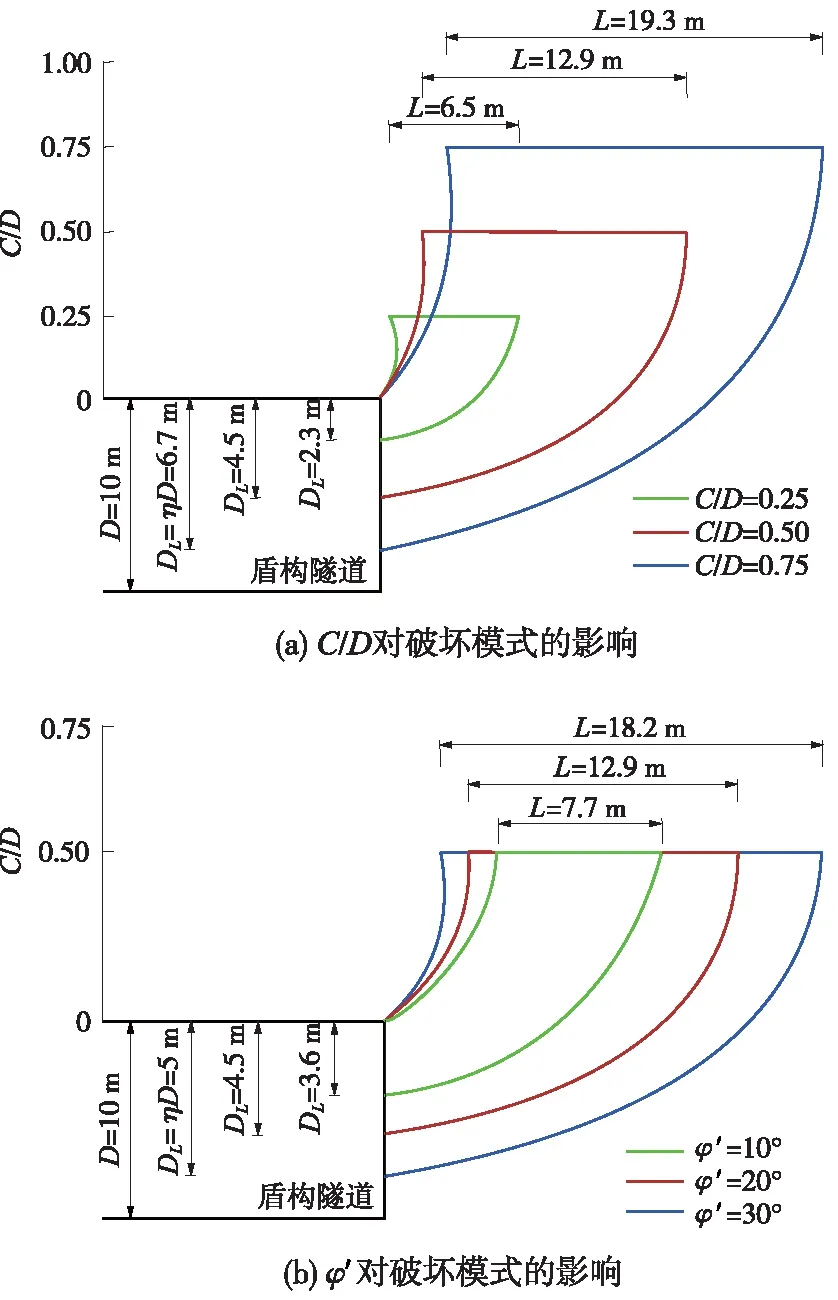
图5 开挖面局部被动失稳的破坏模式

图5(a)为φ′保持在20°的恒定值时,C/D在0.25～0.75之间破坏区域的变化情况。由图5(a)可知,随着C/D的增大,整个破坏区域的形状基本保持不变,而局部破坏比η却线性增加,说明局部破坏区域起源于开挖面下部。随着破坏区域增大,破坏区露出地表的部分在逐渐扩大。当C/D从0.25增加至0.75时,破坏露出地表的长度从6.5 m增至19.3 m,地表破坏块长度总共增加了3倍。图5(b)为C/D保持在0.5的恒定值时,φ′在10°～30°之间破坏区域的变化情况。由图5(b)可知,随着φ′的增加,整个破坏区域的形状及局部破坏比η均在增大,其破坏模式的变化更为复杂。当φ′从10°增加至30°时,破坏露出地表的长度从7.7 m增加至18.2 m。

图6为无量纲系数Nγ随有效内摩擦角φ′变化曲线。由图6可知,Nγ随φ′的增大非线性增加,特别是当φ′>30°时,Nγ值向不同方向发展,其曲线趋于分离。Nγ随着φ′的增加而显著增加这一现象,与SOUBRA等[19]发现的被动系数Kpγ的变化趋势基本一致。图7为无量纲系数Nγ随埋深比C/D变化曲线。由图7可知,Nγ随C/D的增加而线性增加。当φ′值较低(φ′=10°)时,其变化曲线斜率较小;当φ′值较高(φ′=30°)时,其变化曲线斜率较大,且这两条曲线之间的差值随φ′的增大而增大。上述现象说明Nγ对C/D的敏感性随着φ′增大而增大。当土体的有效黏聚力为c′时,式(31)仅包含无量纲系数Nγ和NS,它们均是c′、φ′和η的函数。为研究有效黏聚力c′对极限支护压力的影响,假设盾构隧道埋设于c′和φ′同时存在的黏性土层中。

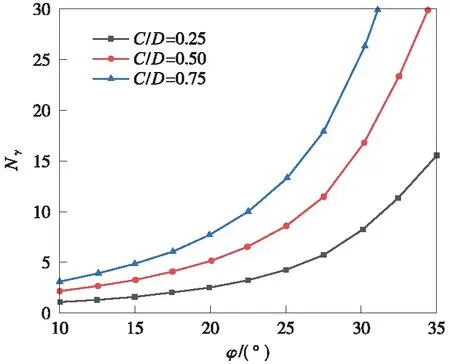
图6 φ′对无量纲系数Nγ的影响

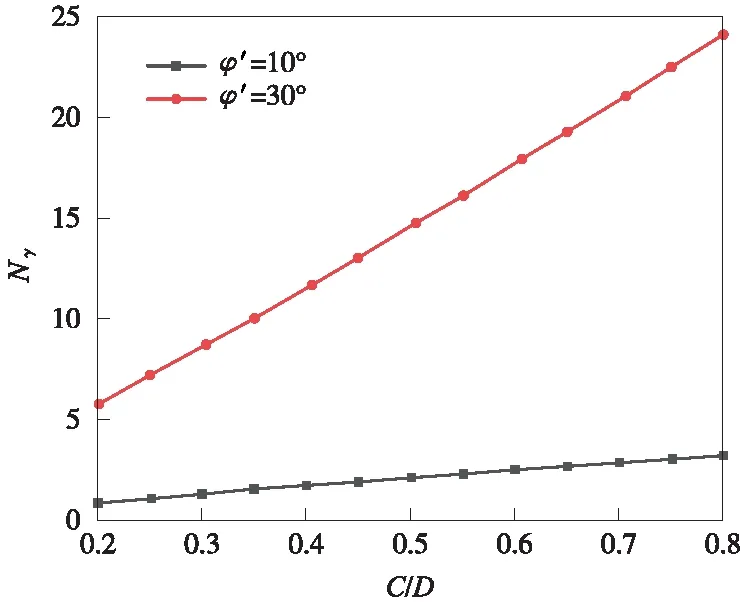
图7 C/D对无量纲参数Nγ的影响

图8为C/D值恒定为0.25时,不同c′值对无量纲系数Nγ的影响。由图8可知,在φ′值相同的情况下,Nγ随着c′的增加而略有增加,而相对于φ′,c′对Nγ的影响要小得多。图9为C/D值恒定为0.25时,不同c′值对无量纲系数NS的影响。由图9可知,NS随φ′的增加而非线性增加,且NS对φ′更加敏感。在φ′值相同的情况下,NS随c′的增大而略有减小。图9中的NS与图8中的Nγ变化趋势相似,因此可以认为c′比φ′对NS的影响要小得多。总而言之,有效黏聚力c′对极限支护压力的影响要比有效内摩擦角φ′小得多。

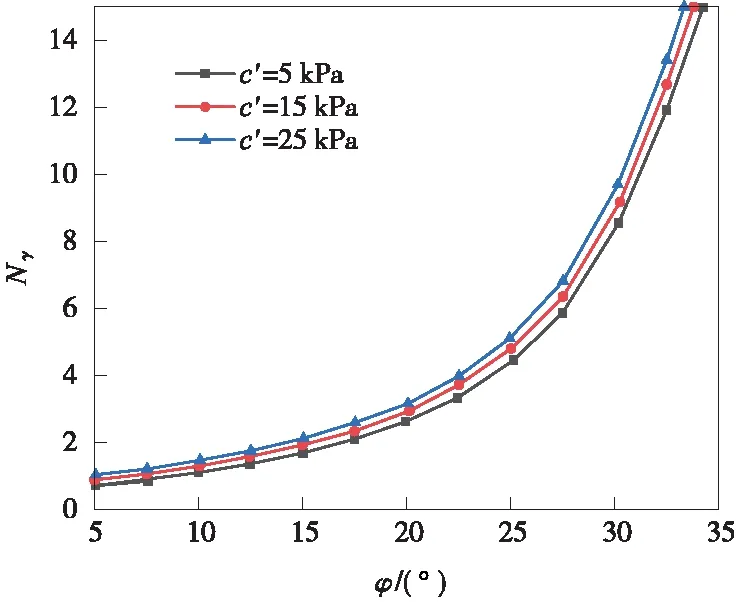
图8 c′和φ′对无量纲参数Nγ的影响

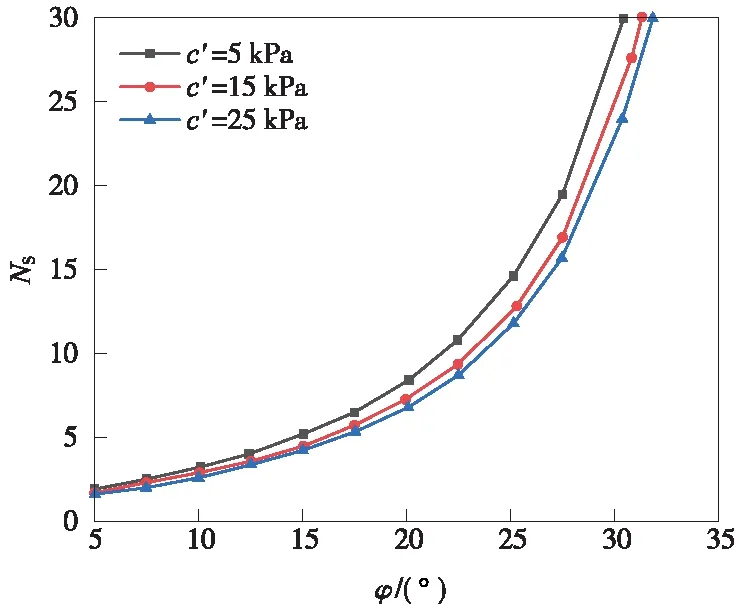
图9 c′和φ′对无量纲参数NS的影响

图10为C/D值变化时,不同c′值对无量纲系数Nγ的影响。从图10(a)中可以看出,在较低的有效内摩擦角(φ′=10°)前提下,若C/D值较小时(C/D=0.25),随着c′的增大,Nγ值只是略有增加;但是随着C/D的增大,c′对Nγ的影响逐渐减弱。从图10(b)中可以看出,当有效内摩擦角较大时(φ′=30°),随着c′的增加,Nγ值几乎保持不变,这说明c′对Nγ的影响随着C/D值增加而增大。

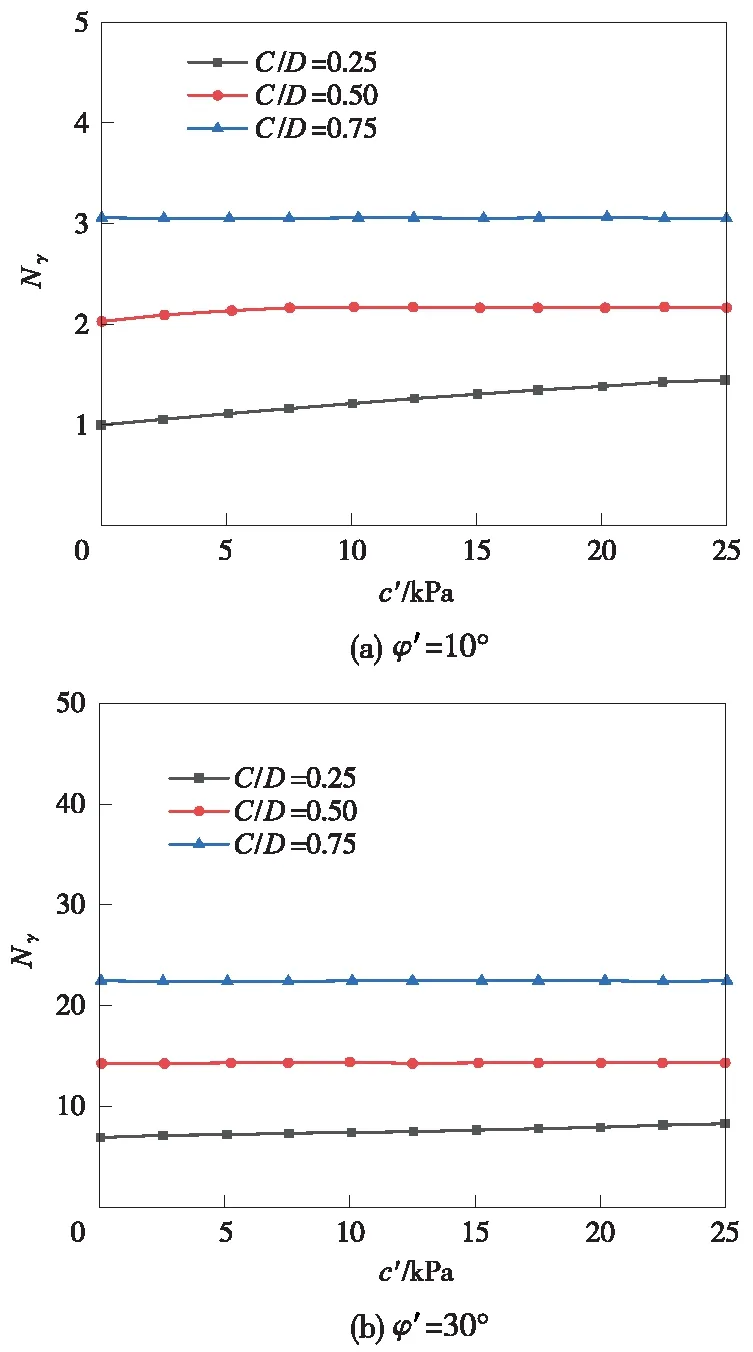
图10 C/D值不同时c′对无量纲参数Nγ的影响

图11为C/D值变化时,不同c′值对无量纲系数NS的影响。从图11(a)中可以看出,在有效内摩擦角较低(φ′=10°)的前提下,若C/D值较小时(C/D=0.25),NS随着c′的增加而降低;若C/D值较大时(C/D=0.75),c′对NS的影响逐渐减弱。从图11(b)中可以看出,当有效内摩擦角较大时(φ′=30°),当C/D=0.25时,随着c′的增加,NS值略有下降。除在C/D相对较低(C/D=0.25)的情况下,NS值始终没有发生变化,这说明c′对NS的影响随着C/D值的增加而增大。

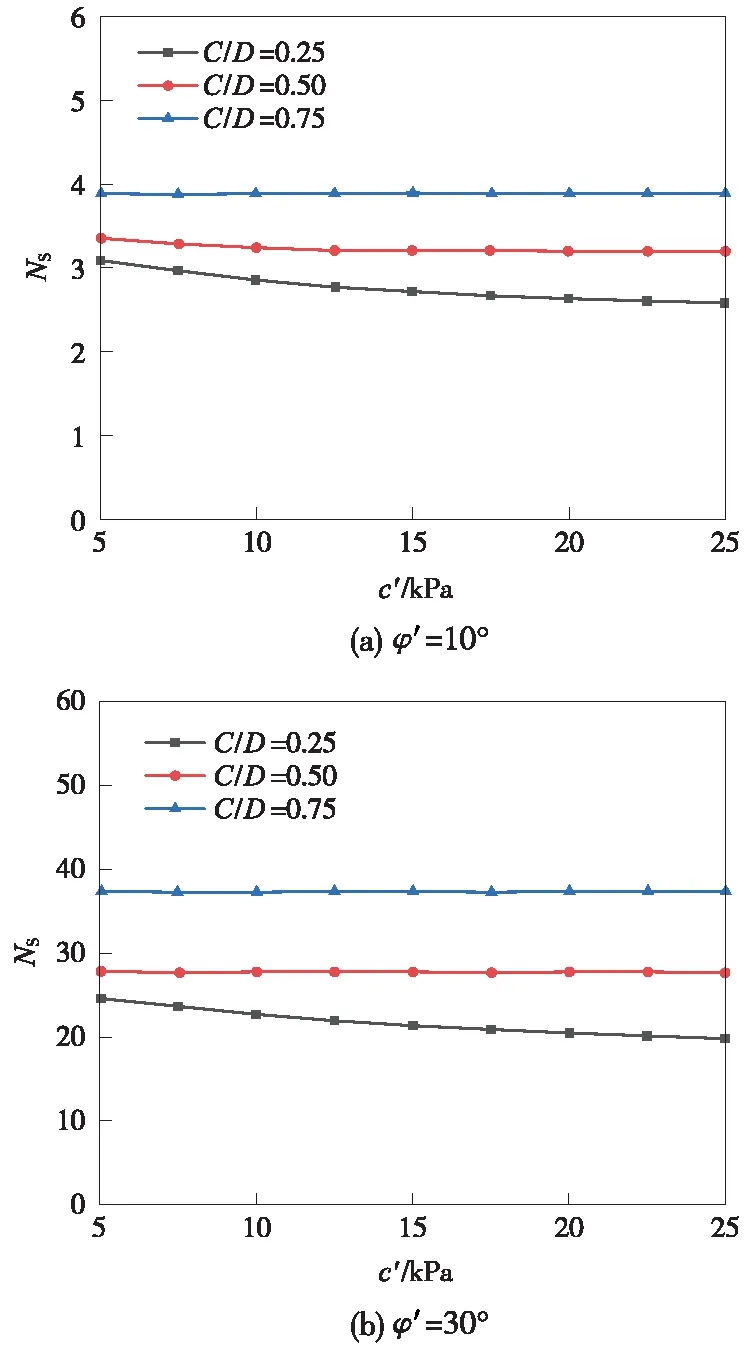
图11 C/D值不同时c′对无量参数NS的影响

2.2 极限支护压力对比

LECA[4]以及MOLLON等[7]均通过上限法计算极限支护压力来评估黏性摩擦土(c≠0 kPa,φ≠0°)中开挖面的被动稳定性,且二者均认为开挖面的破坏区域首先在仰拱处开始发展直至发生全局破坏,即局部破坏比η=1。然而,本文所提出的上限解则是在不假设局部破坏比η的条件下,通过最优化算法求解极限支护压力。因此,为简化计算,以无黏性摩擦土(c=0 kPa,φ≠0°)为例,根据LECA[4]以及MOLLON等[7]提出的局部破坏比η=1时开挖面发生全局破坏的上限解与不提前假设η的本文上限解进行比较,以验证本文所提上限解的合理性以及局部破坏比η对计算结果的影响,极限支护压力的比较分析结果如图12所示。

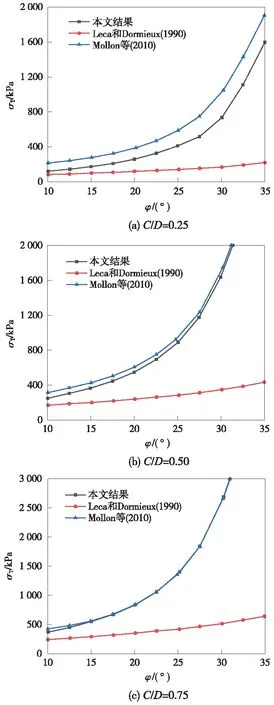
图12 开挖面被动极限支护压力比较

图12(a)为C/D=0.25时不同方法的对比。由图12(a)可知,极限支护压力值随着φ′的增加呈非线性增加,根据本文上限解与LECA的极限支护压力计算结果变化趋势相似,但随着φ′增加二者的差值不断变大。这是因为LECA的解是假设破坏机制是由一个四边形组成的刚性块体,于是可以认为LECA提出的破坏机制与实际情况差距较大。然而,MOLLON与本文的极限支护压力虽然存在一定差距,但是不论φ′值如何变化,其变化趋势基本一致。这是因为MOLLON认为开挖面发生全局破坏并没有考虑开挖面的局部破坏特性,于是采用本文提出的二维破坏机制所计算的极限支护压力要比MOLLON的结果小得多。另外,造成这种差距的另一个原因这因为MOLLON假设破坏的起点位于盾构隧道的仰拱处,而本文认为:当C/D=0.25时,土体的破坏源于盾构隧道仰拱上方的某个深度处,而开挖面发生全局破坏时(η=1),其破坏机制往往会高估失稳的风险。

图12(b)为C/D=0.50时不同方法的对比。由图12(b)可以看出,本文与MOLLON的计算结果非常接近,这两种计算结果之间的差异随着φ′的增加而减小。如表1所示,当φ′从10°增加至30°时,η的值从0.62变化到0.94,其值接近于1;这与MOLLON所假设的开挖面全局破坏一致。而LECA所预测的极限支护压力比本文的结果要低得多。图12(c)为C/D=0.75时不同方法的对比。由表1可知,在C/D=0.75的前提下,当φ′从10°增加到30°时,η的值从0.93变化到1.00。综上所述,本文与LECA的计算结果在φ′≤15°且η=1的条件下相差不大;而本文与MOLLON计算结果在φ′>15°且η=1的条件下却是一致的。因此,当η=1时,LECA以及MOLLON提出的上限解是本文上限解的一种特解。

3 数值模拟对比分析

3.1 工程背景

以我国某大直径盾构隧道工程为背景,将本文提出的上限解应用到实际工程中进行验证,该工程采用φ11.6 m的土压平衡盾构机进行掘进施工,工程地质情况如图13所示。本工程盾构机从SK5+800段始发,其拱顶上方覆土厚度约5 m。盾构始发段线型略微倾斜,以保持较厚的土层覆盖在隧道顶部,盾构隧道主要穿越砂质粉土地层。其中,砂质粉土物理力学参数为:γ=18.8 kN/m3,c′=6 kPa,φ′=25°,E=20 MPa,ν=0.2。

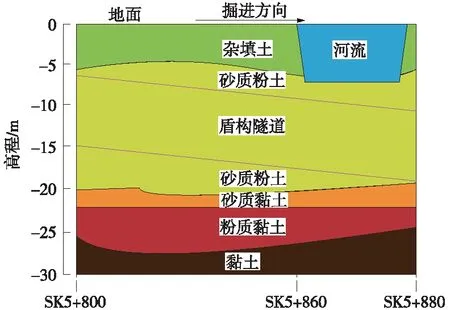
图13 工程地质条件剖面

在盾构掘进过程中,必须不断调整仓内土压以平衡刀盘前方持续变化的土水压力。当盾构机靠近河流底部SK5+860段时,隧道拱顶上方的覆土厚度突然下降到2.5 m左右。这种覆盖厚度的降低会引起开挖面前方土水压力突降,极易发生盾构隧道开挖面被动破坏事故。因此。在计算极限支护力时,取盾构隧道直径11.6 m,拱顶覆土深度2.5 m,河床距离盾构隧道2.6 m,水位高于河床2 m。

3.2 数值模型

采用FELA有限元极限分析软件Optum G2建立数值模型,对工程案例进行数值分析。采用Optum G2软件的优点是:无需假设破坏机制就可以通过自动优化算法搜索最优上限解[20]。模型尺寸为60 m×50 m,模型底部为固定边界,模型两侧约束其法向位移,模型顶部自由,数值模型如图14所示。开挖过程采用简化的“一步”开挖法,即向模型内一次性开挖15 m的隧道长度,随后立即在隧道上下两侧约束其法向位移,并忽略地表超载的影响。在开挖面上施加一段梯形分布的可变荷载,并逐渐增大该荷载,当该荷载增大至开挖面前方土体达到被动极限状态时,此时作用在开挖面上的荷载即为极限支护压力,在该荷载作用下开挖面前方土体的位移场即为破坏区域。

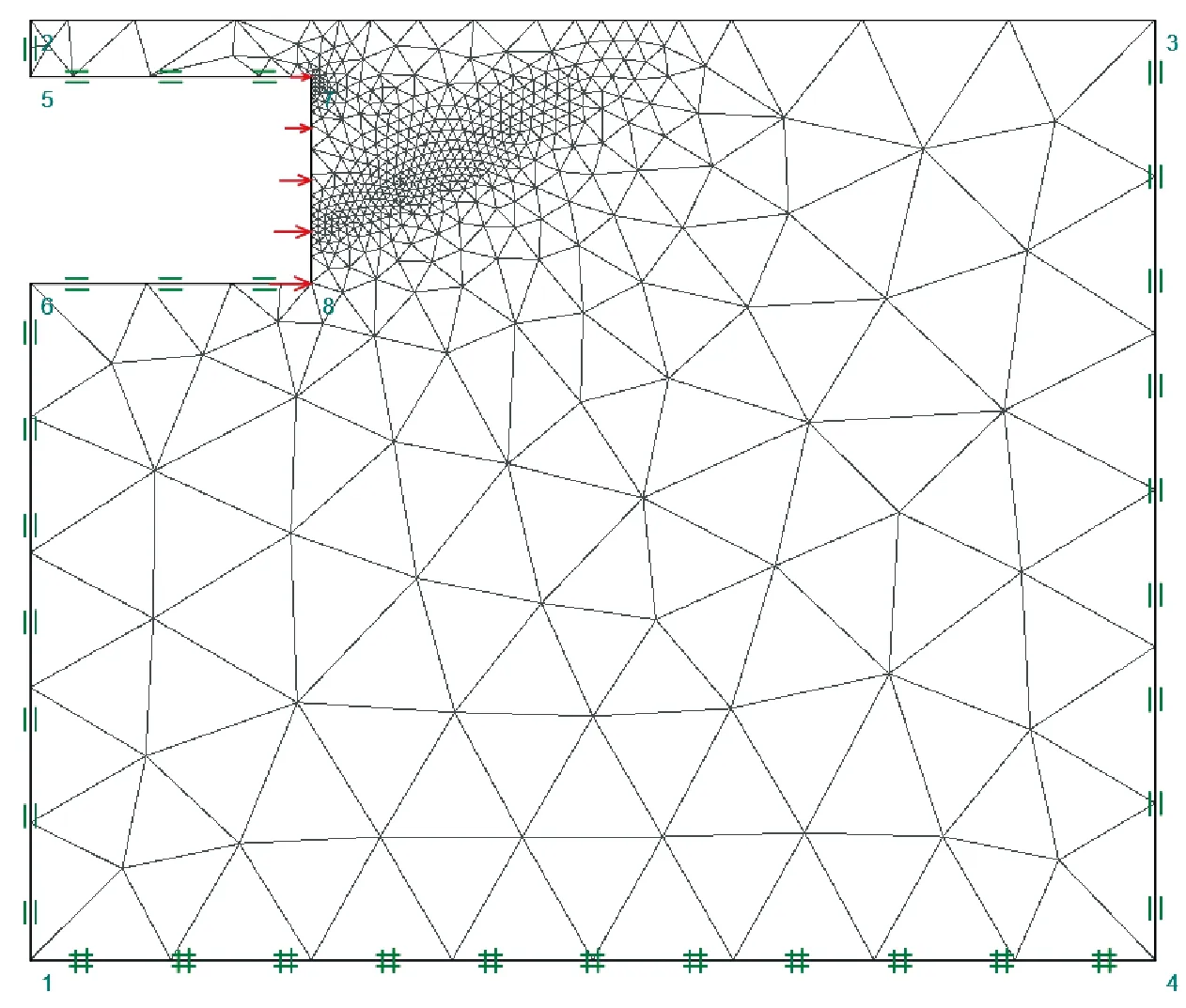
图14 有限元分析模型

3.3 结果分析

将数值模型中砂质粉土物理力学参数以及隧道设计参数分别代入本文及已有方法的上限解中进行计算,通过数值结果与本文所提上限解的结果以及已有上限解(LECA[4]以及MOLLON[7])的结果进行比较,如表2所示。由表2可知,由于LECA和MOLLON均是假设开挖面发生全局破坏时所计算的极限支护压力,所以在局部破坏比η=1的前提下二者的计算结果分别为252 kPa和680 kPa,因此,已有方法的计算结果表明,开挖面的被动破坏均起源于盾构隧道的仰拱处且发生全局破坏。而将上述计算参数代入本文所提出上限解中,根据如图4所示的Matlab的最优化算法,在不假设局部破坏比η的前提下所求得的极限支护压力为625 kPa,局部破坏比η=0.56。数值模拟则是通过软件内部自带的自动优化算法,同样不假设局部破坏比η来搜索最优值,其极限支护压力的数值计算结果为562 kPa,局部破坏比η=0.63。

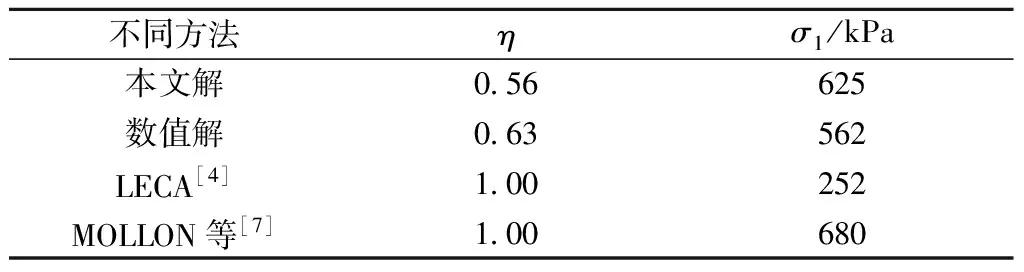
表2 计算结果

因此,本文上限解的计算结果相对较小,且极限支护压力与局部破坏比均和数值计算结果最为接近。然而已有方法的上限解均需要假设局部破坏比η=1,这对于评估浅埋大直径盾构隧道开挖面局部破坏的被动稳定性似乎是不合理的。为验证本文所构建的破坏机制的合理性,将本文提出的破坏模式与数值模拟的破坏区域进行对比,如图15所示。对比发现,本文结果预测的破坏区域较数值结果略大,但在一定范围内与数值结果吻合度较高。

图15 破坏模式对比分析

通过工程案例的计算分析发现,不论是极限支护压力还是破坏比以及破坏区域范围,本文计算结果均与数值结果最为贴近,说明通过本文上限解来评估开挖面的被动稳定性是合理且可行的。另外,在达到LECA及MOLLON预测的极限支护压力之前,开挖面上部存在失稳破坏的可能性。因此,在施工过程中,对于仓内土压需要留有一定的富余来保证施工安全,一般取安全系数2.0。针对本工程的计算结果,建议将仓内土压控制在300 kPa左右,便可以较好地维持开挖面的稳定。而在实际工程中,实测的仓内土压值在200～275 kPa范围内,与本文上限解的建议值非常接近。

4 结论

本文建立了浅埋大直径盾构隧道开挖面的二维被动破坏机制,该机制考虑了仓内土压梯形分布和开挖面局部破坏的影响,并采用极限分析法,推导了开挖面极限支护压力的上限解。其主要研究结论如下。

(1)对于无黏性土,极限支护压力是土体有效内摩擦角φ′和埋深比C/D的函数,二者对极限支护压力的影响较为敏感,有效内摩擦角φ′和埋深比C/D共同决定了局部被动破坏的起点。对于黏性土,极限支护压力是φ′、C/D以及有效黏聚力c′的函数,但是有效黏聚力c′对极限支护压力的影响相对较小。

(2)将本文上限解与已有方法的极限支护压力计算结果进行比较,发现本文提出的上限解是盾构隧道被动稳定性分析的一般解,而LECA和MOLLON的上限解是本文上限解的一种特解,这是因为已有方法均是假设由隧道仰拱处开始引发开挖面全局破坏。结合工程案例的计算分析表明,该方法能够合理地评价盾构隧道开挖面的局部被动稳定性。