黄河口黏性非均匀泥沙沉降速度试验研究

2023-11-10陈柏文马俊峰王俊杰巴彦斌

人民黄河 2023年11期

陈柏文，拾兵，王霞，马俊峰，王俊杰，巴彦斌

（1.中国海洋大学工程学院，山东青岛 266100；2.黄河河口管理局利津黄河河务局，山东东营 257091）

0 引言

黄河口属弱潮型河口，黄河流域来沙量比潮流、波浪的泥沙搬运量大很多［1］，约有80%的黄河来沙絮凝沉降在河口区域［2］，极易形成淤积型三角洲。黄河口泥沙属于黏性细颗粒，具有复杂特殊的电化学性质，受电化学作用、化合物作用以及网捕作用的影响，黏性细颗粒泥沙易在水中形成絮团，会对河口海岸的变迁、河道冲淤等产生影响［3－4］。除上述作用影响外，张金凤等［5］还通过碰撞模拟，认为絮凝体的形成在于颗粒间的碰撞，并提出几种主要颗粒碰撞机制：布朗运动、悬浮颗粒不等速沉降、速度梯度或流速剪切。国内外研究已发现诸如泥沙浓度、泥沙粒径、盐度、温度、分形维数以及紊动剪切强度等影响泥沙沉降的因素［6－11］。

当前测量泥沙沉降速度的方法主要有Mclaughlin法、中值沉速法、Rouse 公式拟合法、基于图像灰度的沉速试验法、LISST 和OBS 结合法等［12－13］。随着学科不断交叉，研究人员从不同的角度研究影响泥沙沉速的因素：通过分形理论与分形维数在泥沙沉降研究中的应用，周银军等［14］指出分形维数能很好地描述泥沙颗粒物理特性、群体泥沙组成、沉积物排列方式以及细颗粒泥沙絮凝体结构；张宇卓［15］基于介观尺度的耗散粒子动力学方法，建立了包含力场势函数的均匀各向同性紊流模型，分析了泥沙浓度、电荷量、紊动剪切对泥沙絮凝的影响。但已有研究成果大都不能揭示絮凝后的絮团颗粒粒径的级配情况，且在絮凝体沉降速度的计算中采用絮凝体中值粒径来代替实际的絮团粒径，实际上不同粒径的絮凝体所占的比例并不相同，计算絮凝体沉降速度时采用中值粒径会导致结果发生偏差。本文应用分形理论以及激光粒度分析仪对斯托克斯公式进行完善，采用加权粒径代表絮凝体的真实粒径，并将完善后的斯托克斯公式应用到黄河口的泥沙沉降速度计算中，以期为更好地认识黏性细泥沙的絮团发育和沉降过程提供可靠的依据。

1 原理与方法

1.1 公式推导

Kranenburg 指出，在一个粒径为D的絮凝体中有k个初始粒径为Dp的黏性细泥沙颗粒［16］，则：

式中：nf为絮凝体的分形维数。

由式（1）可以得到单颗絮凝体的质量：

式中：m1为单颗絮凝体的质量，α为初始泥沙颗粒球形度系数，ρs为初始泥沙颗粒密度。

假设某层水体中含沙量为C，则该层水体中絮凝体质量为

式中：l为沉降桶的长度，d为沉降桶的宽度，h为该层水体的厚度。

由式（1）～式（3）可以得到某层水体中絮凝体个数为

式中：β为絮凝体颗粒球形度系数，ρf为絮凝体密度。

由式（4）～式（5）可得絮凝体密度：

式中：ρw为水的密度，Δρf为絮凝体有效密度。

随着激光粒度分析仪的应用普及，王国梁等［17］推导出体积分形维数计算公式，该公式不需要作不同粒级土壤具有相同密度这一假设，所以比质量分维模型更具有合理性，其计算公式为

斯托克斯公式：

式中：ωs为泥沙颗粒的沉降速度，μ为沉降桶中水的动力黏滞系数，g为重力加速度。

应用斯托克斯公式时把球形度系数α和β作为1处理［18－19］。激光粒度分析仪可以测出48 组絮凝体粒径以及它们所占的体积百分含量，且每组絮凝体粒径所占比例各异［20］，为更好地体现絮凝体的实际粒径，尝试采用加权粒径代替中值粒径来完善斯托克斯公式。完善后的斯托克斯公式如下：

由式（6）～式（10）可推导出泥沙沉速公式为

式中：Pi、Pj分别为絮凝后和絮凝前第i、j组颗粒粒径所占的体积百分含量；Di、Dpj分别为絮凝后和絮凝前第i、j组颗粒粒径。

而加权粒径Dw的计算公式为

令Dw为絮凝体的加权粒径，Dpw为初始泥沙颗粒加权粒径，则最终的沉速计算公式为

1.2 公式验证

采用实测泥沙沉速资料［21］对式（13）的合理性以及计算结果的精度进行验证，采用均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）进行有效性评定，各项误差的值越小，表明有效性越高。

由式（13）计算的沉速与实测资料对比如图1 所示，计算值与实测值关系的决定系数R2为0.943，RMSE、MAE 和MAPE 均在10%以内，即计算值与实测值吻合良好，有效性高，说明式（13）可用于细泥沙颗粒沉降速度的计算。孟若霖等［22］运用斯托克斯公式计算得到上述实测资料的泥沙沉降速度（采用中值粒径计算），计算值与实测值的决定系数R2仅为0.782。主要原因是加权粒径代替中值粒径后，絮凝体粒径体积占比不均的问题得以解决，泥沙沉降速度不会因中值粒径体积百分含量过小而出现偏差，加权粒径使得结果代表性更好。因此，采用加权粒径来推求泥沙沉降速度比采用中值粒径来推求具有更高的准确性。

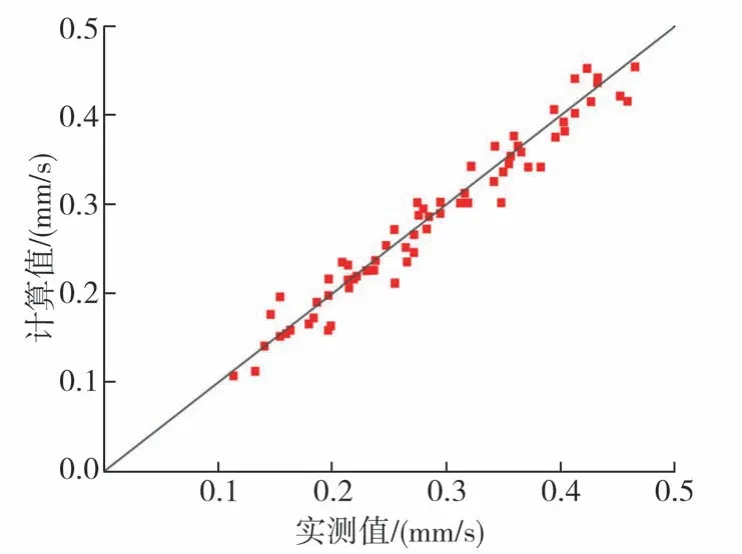
图1 沉速计算值与实测值对比

2 采样地点及测量手段

本试验采用黄河口的黏性细颗粒泥沙进行以含沙量和盐度为影响因素的静水沉降试验研究。试验沙样取自黄河口三角洲水域。利用激光粒度分析仪测得试验时悬浮泥沙中值粒径为13.28 μm。

沉降试验采用自主设计开发的大型温控自动搅拌沉降试验矩形桶以及山东耐克特激光粒度分析仪。沉降桶尺寸为1.1 m×0.3 m×1.5 m（长×宽×高），内置温度计、水位计、OBS3＋浊度仪（量程0～4 000 NTU）、可控型升温保温装置以及搅拌装置曝气泵等。试验将整个水深均匀划分为6 层，并采用OBS3＋浊度仪和激光粒度分析仪对不同悬沙浓度（2、5 kg／m3和7 kg／m3）、不同盐度的水样进行浊度和泥沙颗粒粒径分布的测量，分别记录底层初始浊度、初始泥沙颗粒粒径、底层浊度为初始浊度50%时的时间及对应的絮凝体颗粒粒径。

3 试验结果与分析

3.1 OBS3＋的参数率定与使用

本次试验絮凝泥沙颗粒取样采用陈曦［23］的中值沉速法，即底层含沙量为初始含沙量的50%时进行取样。试验前对OBS3＋浊度仪进行参数率定，浊度与含沙量的关系如图2 所示，拟合曲线决定系数为0.994。

图2 OBS3＋测量浊度值与含沙量的关系

根据浊度与含沙量的关系以及OBS3＋记录的浊度，可得沉降桶内随时间变化的泥沙相对浓度，为使泥沙相对浓度随时间的变化过程更加直观，以含沙量为7 kg／m3的泥沙沉降过程为例，利用数学模型进行曲线拟合，如图3 所示。

图3 泥沙相对浓度及曲线模型拟合

1）盐度为0～11‰时，泥沙相对浓度随时间变化可用反比例函数来描述，但低盐度条件下泥沙相对浓度变化较为缓慢，且随着盐度增大泥沙相对浓度变化加快，因此低盐度下泥沙相对浓度表达式为

式中：SRC为泥沙相对浓度，S为盐度，t为泥沙沉降时间，tmax、tmin分别为泥沙絮凝沉降的最大时间、最小时间。

拟合曲线决定系数R2＝0.996。

2）盐度为11‰～25‰时，中高盐度下泥沙相对浓度随时间变化相对较快，随着盐度增大泥沙相对浓度变化会减缓，但其过程同样可用反比例函数来进行描述：

拟合曲线决定系数R2＝0.984。

利用数学模型，可得出在确定温度和含沙量条件下不同盐度和时间对应的准确SRC值，并预测泥沙相对浓度随时间的变化趋势。图3 表明，同一沉降桶中不同盐度的水样底层泥沙相对浓度随时间逐渐减小，且随着盐度的增加底层泥沙相对浓度达到50%的时间呈现先减小后增大的趋势，达到泥沙相对浓度为50%的时间基本为20～60 min，在盐度11‰下时间达到最小值。

根据数学模型表达式可得到不同盐度下底层泥沙相对浓度达到50%的时间，运用前文所提出的方法，可以得到相对应时间下絮凝体颗粒粒径分布、加权粒径以及分形维数，进而利用式（13），可以求得不同含沙量和盐度下絮凝体的沉降速度。

3.2 盐度与含沙量对絮凝体沉降速度和粒径的影响

1985 年，Azzalini［24］首次提出比正态分布适用范围更广的偏正态分布，其随机变量x的密度函数如下：

式中：φ、Φ分别为标准正态分布的密度函数和分布函数，η、σ分别为正态分布的位置参数和形状参数，λ为偏态参数，当λ＞0 时右偏。

为系统描述以及预测泥沙絮凝沉降速度随含沙量和盐度的变化趋势，采用考虑盐度和含沙量影响因子的偏正态模型对低含沙量的絮凝体沉降速度与盐度关系进行参数以及曲线拟合（ωs为絮凝体沉降速度，取其数值部分并记为ω），则带参数的数学模型表达式为

式中：ω为絮凝体沉降速度数值，C为含沙量，S为盐度，k、b、d为待定系数，t为积分变量。

基于式（17）的拟合结果如图4 所示。

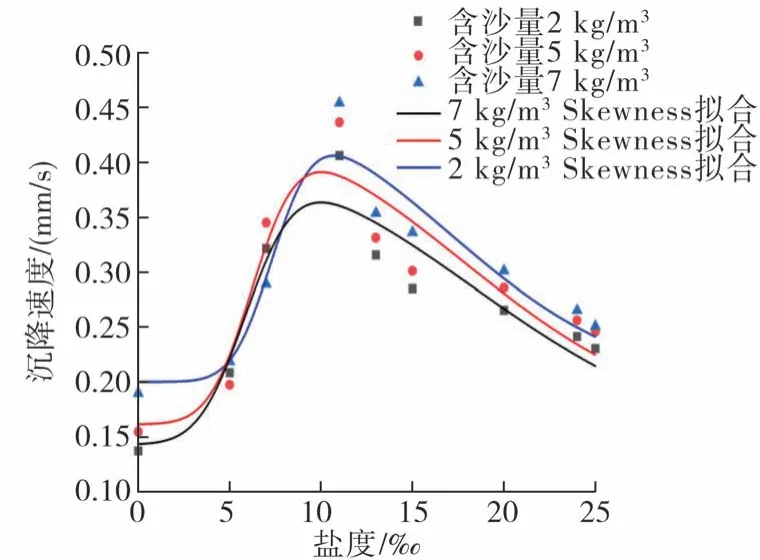
图4 低含沙量下盐度与沉降速度关系

在确定初始粒径的条件下，考虑盐度和含沙量影响因子的絮凝体沉降速度数学模型表达式为

拟合曲线决定系数R2＝0.905，λ值取6。

而由试验数据以及以往研究表明的盐度与絮凝体粒径关系可知［6，8］，偏正态分布模型仍然可用于描述盐度对絮凝体粒径的影响过程。前文指出Dw为泥沙絮凝体加权粒径，现取其数值部分并记为Df，因此在确定初始粒径的条件下由式（17）可得其拟合曲线图（见图5）。

图5 盐度与絮凝体粒径关系

其数学模型表达式如下：

式中：Df为泥沙粒径数值。

拟合曲线决定系数R2＝0.947，λ值取3.5。

依据偏态分布模型的拟合曲线，可以看到部分计算值高于拟合点，原因是本试验尚未完全考虑影响泥沙絮凝沉降的全部因素，且斯托克斯公式中把球形度系数近似取为1 不尽合理。为验证模型的适用性，现将偏正态模型用陈曦试验数据进行曲线拟合，结果如图6 所示。

图6 陈曦试验数据对偏正态模型的验证结果

由图4～图6 可知，本试验得到的絮凝体沉降速度为0.11～0.45 mm／s，加权粒径为21.1～46.5 μm。在2、5、7 kg／m3含沙量的沉降桶中，随着盐度的增加，絮凝体沉降速度和粒径均呈现先增大后减小的趋势，从盐度0 到盐度11‰，沉降速度和粒径逐渐增大，从盐度11‰到盐度25‰，沉降速度和粒径逐渐减小。在含沙量7 kg／m3、盐度11‰处取得最大沉降速度0.45 mm／s，对应最大加权粒径46.5 μm，在含沙量2 kg／m3、盐度0 处达到最小沉速0.11 mm／s，对应最小加权粒径21.1 μm，达到泥沙浓度相对含量50%的时间基本为20～60 min。这些试验结果与陈曦试验的结果基本一致，且偏态分布模型与陈曦试验数值拟合良好，拟合曲线决定系数R2＝0.944，说明模型准确度较高，适用于其他河口或试验的絮凝沉降速度研究。

泥沙颗粒表面带负电荷，在静电作用下呈现独特的双电子层结构，而盐度的增大使得沉降桶中阳离子的浓度增加，双电子层厚度减小，从而使得泥沙颗粒间的静电斥力作用减弱，在同等范德华力作用下，泥沙颗粒相互吸引碰撞形成粒径更大的絮凝体，沉降速度随之增大。而盐度的继续增大则会导致电势逆转，颗粒间斥力不断增大，抑制泥沙絮凝体的发育，沉降速度也随之减小。而在低含沙量条件下，含沙量的增加提高了泥沙颗粒的碰撞概率，有利于发育形成更大的絮凝体，沉降速度也因此增大。李学凯等［25］指出随着硫酸钾浓度的不断增大，沉降速度也不断增大，在硫酸钾浓度增加到60 mmol／L（换算盐度为10.45‰）时，达到最大沉速，期间沉降速度从0.23 mm／s 增加到1.42 mm／s。与本文结果相比可知，两者沉降速度变化趋势基本相同，只是在整体上絮凝体的沉降速度本文结果略小一些。王尚毅［26］则提出静水条件下絮凝体沉降速度随着盐度的增大呈现出先增大、到达一定盐度后再减小的趋势，沉降速度为0.13～0.35 mm／s。王家生等［27］研究阳离子浓度对黄河泥沙沉降速度的影响，提出絮凝体沉降速度在0.25 mm／s 附近。这些结论均印证了本试验结果的正确性。

3.3 黄河口泥沙最佳絮凝盐度

黄河三角洲河口泥沙的沉降、淤积、输移与扩散对黄河河口的变迁与下游河道的安全具有重要意义，而黄河口泥沙最佳絮凝盐度则是河口整治的重要一环。由图7 可知，随着盐度的增大，絮凝体粒径和絮凝体沉降速度变化趋势保持一致，即盐度在0～11‰之间时，絮凝体粒径和沉降速度都随着盐度的增大而增大，盐度在11‰～25‰之间时，絮凝体粒径以及沉降速度都呈现减小趋势，且不同含沙量条件下泥沙絮凝体的粒径、沉降速度均在盐度为11‰处达到最大值，故可认为泥沙絮凝的最佳盐度为11‰。冯曦等［28］在对黄河口泥沙特性的研究中提出在不同盐度下黄河泥沙静水沉降的最佳絮凝盐度为15‰左右。李芳等［29］在对高岭土的静水沉降试验中指出其最佳絮凝盐度为13‰左右。李学凯等［25］指出黄河泥沙最佳絮凝盐度为10.45‰左右。