基于FEA的复合材料结构极限承载失效预测

章 凌，赵优存，李 祎，杨 帆，崔 浩

(1.北京宇航系统工程研究所，北京 100076；2.西北工业大学民航学院，太仓 215513)

0 引言

连续纤维增强树脂基复合材料是以树脂聚合物为基体、连续纤维等为增强材料，通过复合工艺制备而成的高性能材料，具有高比强度、高比刚度和耐腐蚀等诸多优点[1]，广泛应用于C929宽体客机、长江系列涡扇发动机以及新一代运载火箭等国产重大装备[2]。

对于纤维增强复合材料的损伤分析，由于试验成本较高，业内广泛使用有限元对试验进行模拟仿真，并且通过渐进损伤模型预测复合材料结构的失效过程[3]。现有有限元软件的内置损伤材料模型多数基于二维层合板理论，有限元分析 (Finite Element Analysis，FEA)软件中虽然内嵌三维正交各向异性模型，但仍然缺乏三维失效判据[4]，这导致当使用内嵌Hashin、LaRC03等失效判据进行失效判断或通过用户自定义子程序引入其他失效判据时，常需要针对层合板每一层分别建立单层模型[5-6]。这种较为精细的模型计算效率低，计算时间长，为此，Chou等[7]提出一种关于复合材料层合板的三维等效弹性常数计算方法，通过各单层板的属性可计算出层合板的三维等效弹性常数，从而显著提高复合材料层合板，特别是厚板问题的计算效率，但Chou等仅是通过该方法对一简单的层合板问题进行研究，得出各层对应的应力、应变场，仍未解决层合板的失效问题。在此方法基础上，Bogetti等[8]针对厚板的失效问题，在多尺度计算方法中加入损伤准则，并基于FORTRAN语言编写有限元子程序求解厚板问题；Staniszewski等[9]在Bogetti的工作基础上增加了材料的非线性，完善了材料的响应。上述两种针对厚板的多尺度损伤计算方法，需要在计算过程中不断获取单元的信息，包括材料以及铺层信息，这种读取会造成计算效率的降低，贾利勇等[4]基于上述研究成果针对厚板问题提出了一种新的非线性多尺度分析方法，该方法通过刚度等效和应力-应变分解建立了一种多尺度分析模型，实现了复合材料厚板结构在子层压板水平的计算以及在铺层水平的失效判断，并通过编写子程序对复合材料首层失效进行判断。这种方法仅能判断复合材料首层的失效，无法解决复合材料层合板的渐进失效问题，同时，该方法未考虑层合板处于小应变阶段时各铺层未进入损伤状态，而是在层合板每个应变阶段均对各铺层进行损伤判断，这会导致计算效率降低。

本文采用并行多尺度的方法，基于经典层合板理论根据各单层板的铺层信息以及材料刚度计算层合板的等效刚度。在层合板小应变阶段不考虑各铺层损伤，超出一定应变阈值后，引入多种失效判据对各单层板进行渐进损伤判断，将仿真结果与FEA软件内嵌判据结果以及试验结果进行对比，以验证该方法的效率与准确性。

1 数值模型

1.1 并行多尺度计算流程

基于并行多尺度方法，本文编写的子程序其计算过程如图 1所示。与通常理解的介于宏观-细观-微观体系的多尺度方法不同，本文所指多尺度参考贾利勇等[4]、Bogetti等[8]以及Stanis-zewski等[9]关于厚板问题所提出的多尺度理解，即对于层合板从“层合板整体”到“其中每一层”两个尺度进行分析。基于该方法的层合板有限元模型，一个单元中包含N个铺层，该单元即为一个层合板单元。计算起始时输入各单层板刚度，从而计算得出层合板的等效刚度。层合板在载荷较低时处于线弹性阶段，此时无需对各单层板进行损伤判断；随着加载载荷的增大，当层合板的应变大于预设安全阈值时，开始对每一层单层板进行损伤判断。对损伤后的单层板的刚度进行折减，并反馈计算得出损伤后层合板的等效刚度，最后更新应力矩阵，进行下一个的加载步。

1.2 层合板弹性响应

在并行多尺度方法中，对于层合板有限元模型，一个单元中包含N个铺层，该单元即为一个层合板单元，通过经典层合板理论层合板的等效刚度可由下式计算得出

(1)

(2)

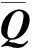
子程序中，通过输入层合板的等效刚度可从FEA有限元软件中反馈计算得到层合板的应变以及应力。当层合板应变值大于预设应变阈值时，进入单层板的损伤判断，基于正交各向异性复合材料的应力应变关系[10]，相对于材料主轴坐标系，单层板面内应力应变关系为

(3)

其中

(4)

式中，σ11，σ22，τ12是单层板的面内应力分量；ε11，ε22，γ12是上述应力对应应变。E1与E2分别是平行于纤维方向和垂直于纤维方向的杨氏弹性模量；G12是面内剪切模量；ν12与ν21为面内泊松比。

单层板层间应力应变关系为

(5)

Q33=E3,Q44=G23,Q55=G13

(6)

式中：σ33，τ23，τ13是单层板的层间应力分量；ε33，γ23，γ13是上述应力对应应变。E3是垂直于单层板平面方向的杨氏弹性模量；G23与G13是层间剪切模量。

1.3 渐进损伤模型

本文针对单层板纤维、基体以及层间3个维度的损伤判断，分别采用基于应力描述的最大应力准则、二维Puck失效准则[11]和Ye分层失效准则[12]来判断各单层板的初始失效。相较于以往学者仅采用一种失效准则对材料的损伤进行分析，此处所界定的3种准则同时对单层板进行3个维度的失效判断仍然合理，原因如下：

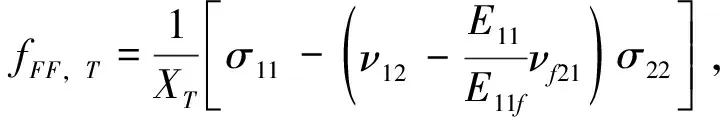
以下是对材料各方向损伤起始的定义，有效应力被用来判定材料的损伤起始，当纤维出现拉伸破坏(σ11≥0)时

(7)

当纤维出现拉伸破坏(σ11<0)时

(8)

相较于二维Puck失效准则，三维Puck失效准则具有更好的预测结果，但后者的理论需要进行额外的算法来搜索潜在的断裂平面，这一步需要消耗大量的计算时间，故此处选择Puck理论的平面应力格式[13]对基体损伤进行简单讨论，二维Puck失效准则认为基体失效有3种模式，即基体拉伸失效(模式A)、基体压缩失效(模式B)以及基体由于更大的压缩应力而失效(模式C)。

当基体出现拉伸破坏(σ22≥0)时，基体破坏为模式A

(9)

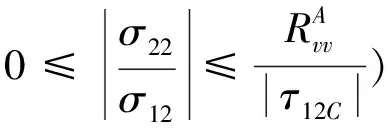
(10)

(11)

当层间出现破坏时

(12)

(13)

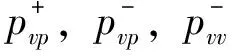
(14)

(15)

在损伤演化方面，采用双线性渐进损伤模式对材料刚度进行折减[15-16]，定义损伤变量为

(16)

式中，δ0为破坏起始点的等效位移，有效位移δ的值为有效应变εeff与单元特征长度LC的乘积，δC为完全破坏时的等效位移，其值由混合模态断裂韧性GT与完全断裂时破坏的应力计算得出。

2 验证试验

本文中测试层合板材料为T800级碳纤维增强复合材料，其材料参数如表 1与表 2所示。

表1 T800级碳纤维增强复合材料模量与泊松比

表2 T800级碳纤维增强复合材料强度值

如图 2所示，开孔拉伸试验试样长度L=250 mm，宽度W=36 mm，开孔直径D=6 mm，层合板铺层方式为[0°]8、[±45°]4S，每一层单层板厚度均为0.15 mm。

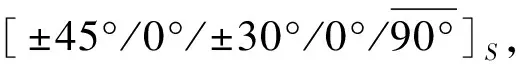
3 算例分析

3.1 单个单元仿真

为验证在FEA软件中损伤演化的准确性，采用单个单元仿真方法对子程序进行测试。如图 4(a)建立1 mm×1 mm单个单元加载模型，在一个端面的4个节点处进行相同大小位移加载，另一端面的4个节点处进行固支。此处对以纤维拉伸方向损伤演化为例，图 4(b)显示了单元双线性损伤演化的过程，红色线为单元应力，蓝色线为单元损伤变量，单元应力不超过2 067 MPa 时单元为线弹性、损伤为0，单元应力达到2 067 MPa时开始发生损伤，此后单元刚度降低、损伤积累，单元损伤达到1.0时完全失效。单元应力峰值为2 067 MPa，与纤维方向拉伸强度值2 071 MPa近似相等。

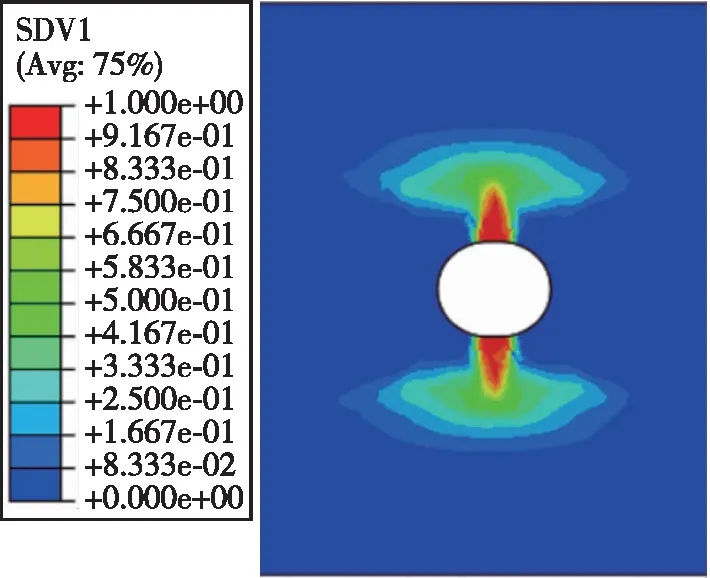
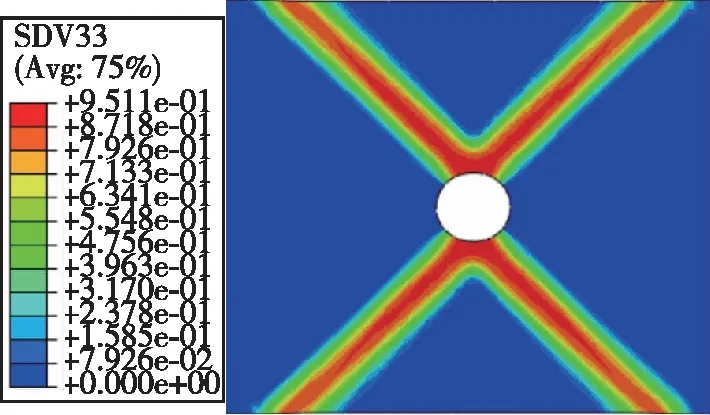
3.2 开孔板损伤分析

图 5与图 6分别是[0°]8、[±45°]4S铺层层合板拉伸试验的并行多尺度计算方法仿真结果以及试验数字图像相关技术(Digital Image Correlation，DIC)结果。可以看出：对于开孔层合板拉伸试验，其损伤主要发生在孔边，[0°]8铺层层合板纤维从孔边起裂并沿着孔板的宽度方向扩展，基体从孔边起裂沿着孔板长度方向扩展，这符合试验完全破坏前一帧的DIC结果，与试验结果相近；[±45°]4S铺层层合板的损伤主要以基体拉伸破坏为主，基体在孔边起裂并沿着45°方向扩展，最后形成X形裂纹，仿真结果同样符合试验完全破坏前一帧的DIC结果。

图 7、图 8分别对应[0°]8、[±45°]4S铺层层合板拉伸的载荷-位移曲线，比较了在相同网格尺寸下的模拟结果与试验结果以及使用FEA软件中内嵌的Hashin损伤准则预测结果。

表 3中为两种不同铺层开孔板拉伸失效载荷的对比，结果表明，在同样网格尺寸的情况下使用本文计算方法得出的失效载荷与试验结果相近，使用本文计算方法能够较为准确地预测开孔板拉伸试验的结果，误差能够保持在5%以下，但在本文计算方法中未考虑剪切非线性的影响，故从图 8曲线中可以看出，针对[±45°]4S铺层层合板拉伸试验的预测，本文方法不能很好地预测损伤前的非线性趋势。

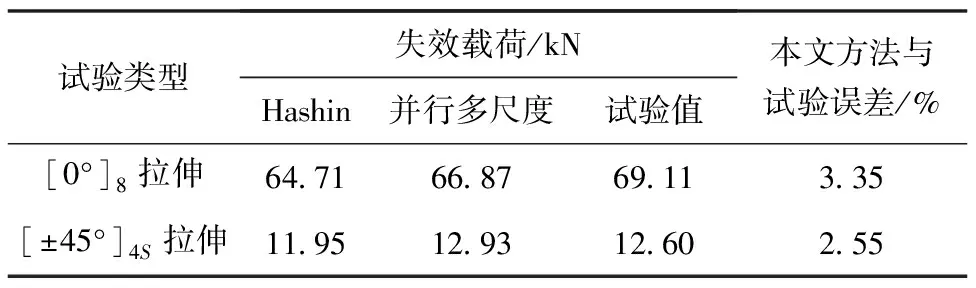
表3 开孔板拉伸失效载荷误差对比

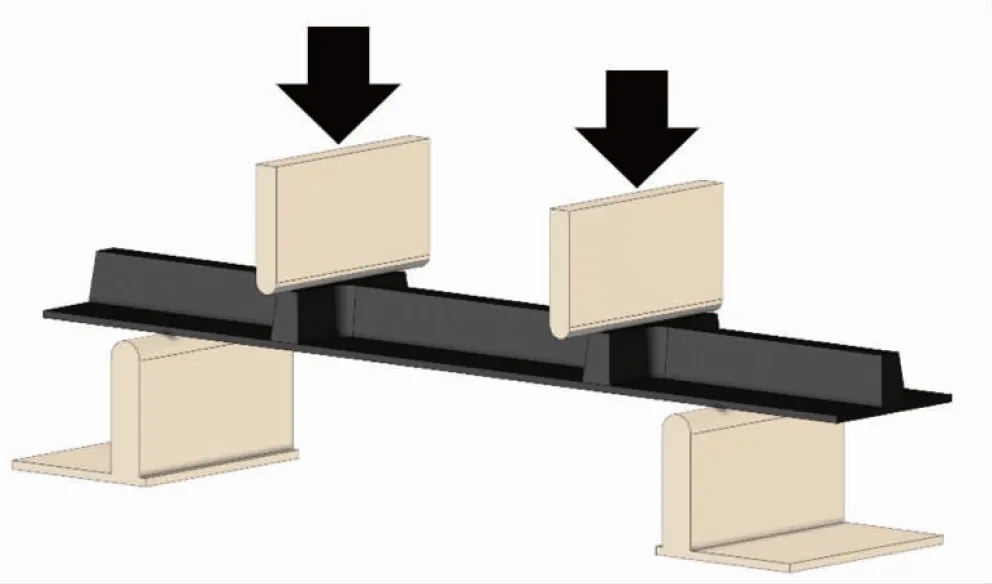
3.3 夹筋板损伤分析

图 9是横跨两筋条四点弯试验的并行多尺度计算方法仿真结果以及试样破坏结果。从仿真结果可以看出，在筋条与蒙皮的连接处首先出现初始裂纹，并且该裂纹沿着筋条连接处扩展至横纵筋条交叉点处，与试验结果相近。

图10为横跨两筋条四点弯试验的载荷-位移曲线，比较了在不同网格尺寸下的模拟结果与试验结果以及使用FEA软件中内嵌的Hashin损伤准则预测结果。

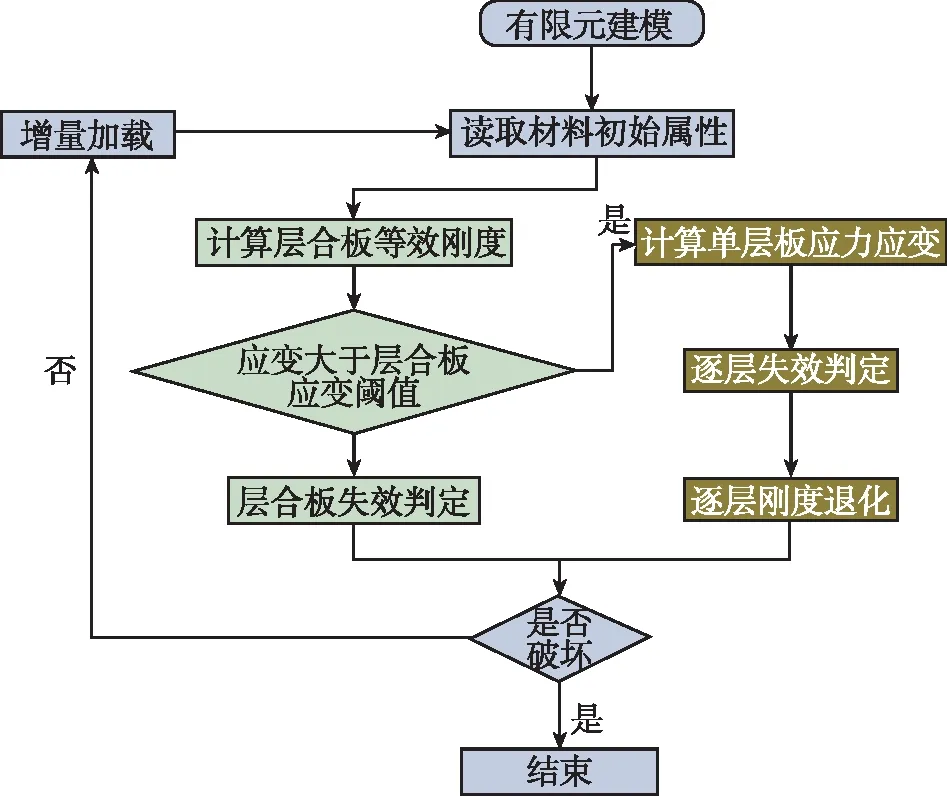
图1 并行多尺度方法计算流程图

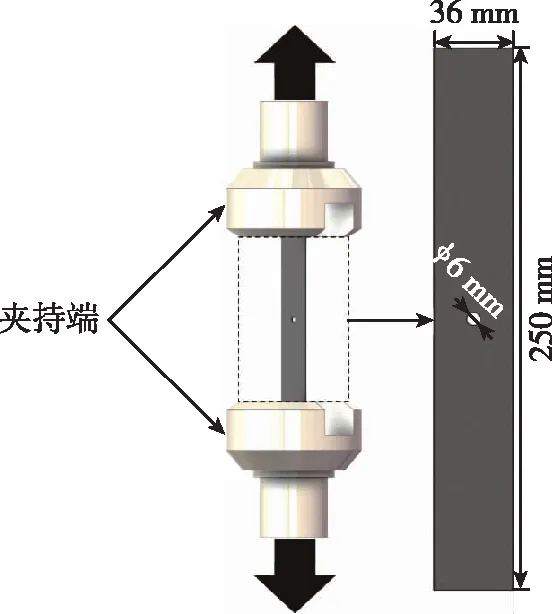
图2 开孔板拉伸几何形状及试验条件

(a)试验条件

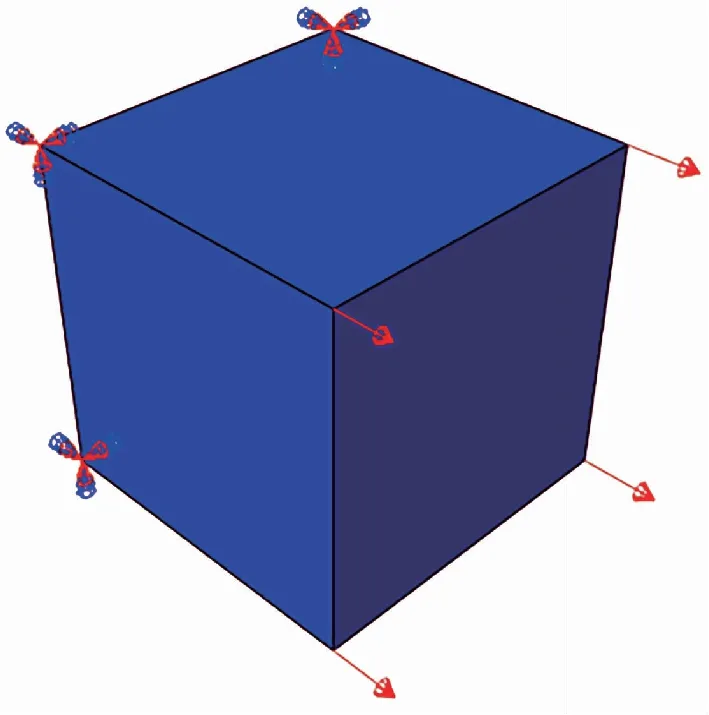
(a)纤维方向拉伸加载

(a)纤维损伤示意图

(a)基体损伤示意图

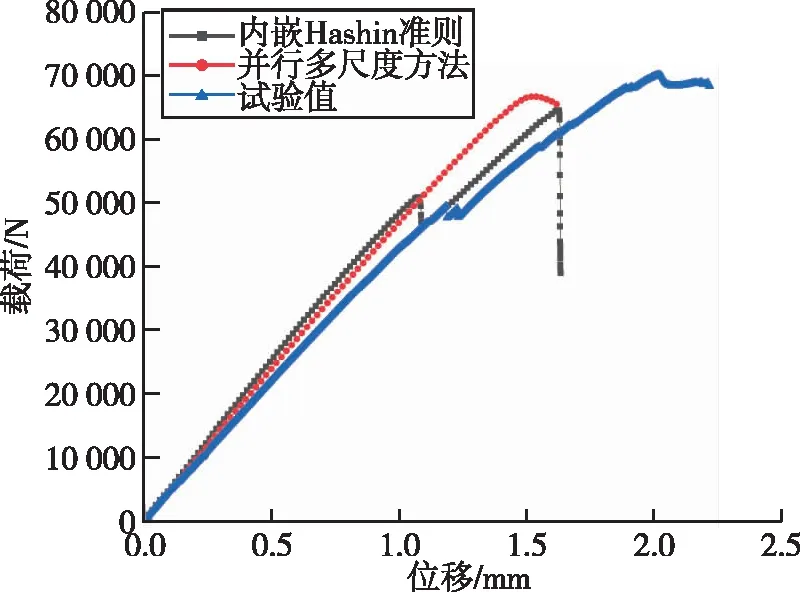
图7 [0°]8铺层层合板拉伸载荷-位移曲线

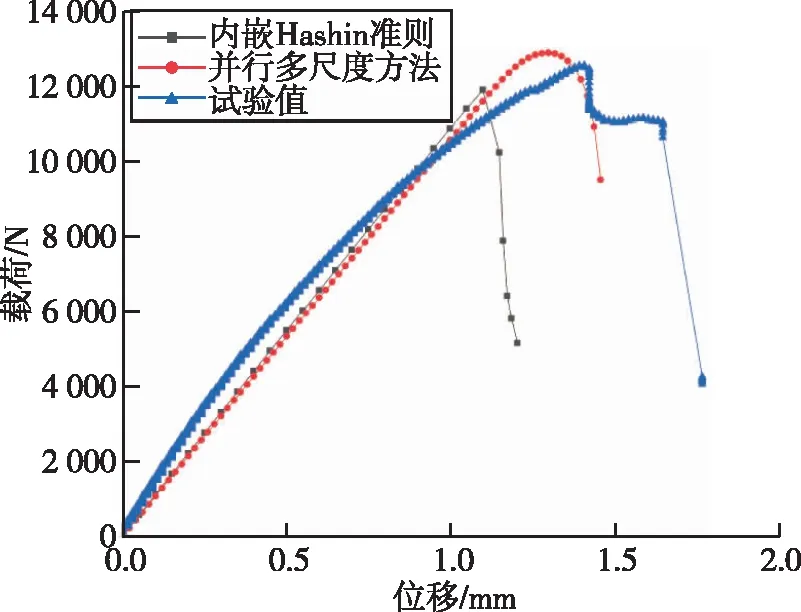
图8 [±45°]4S铺层层合板拉伸载荷-位移曲线

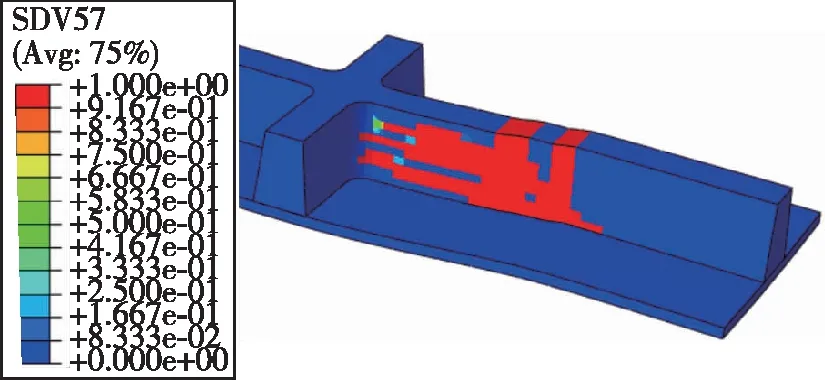
(a)层间破坏

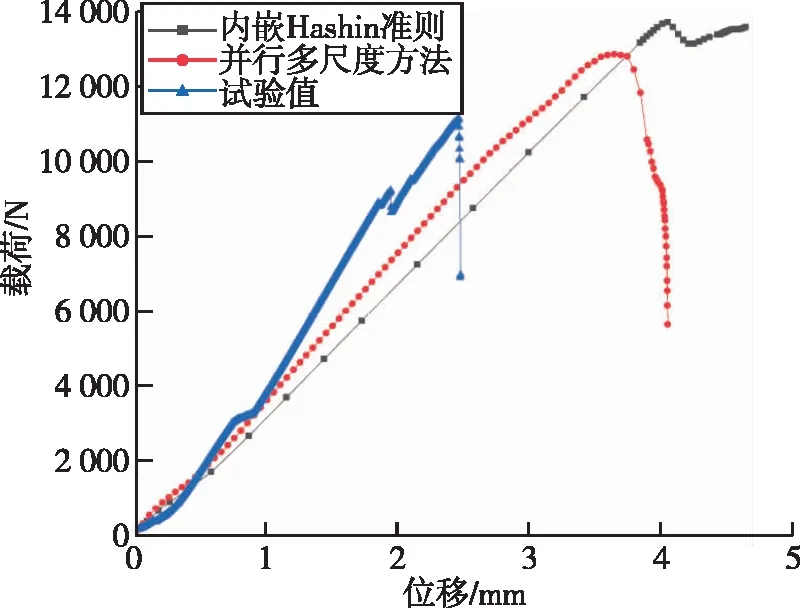
图10 横跨两筋条四点弯试验载荷-位移曲线

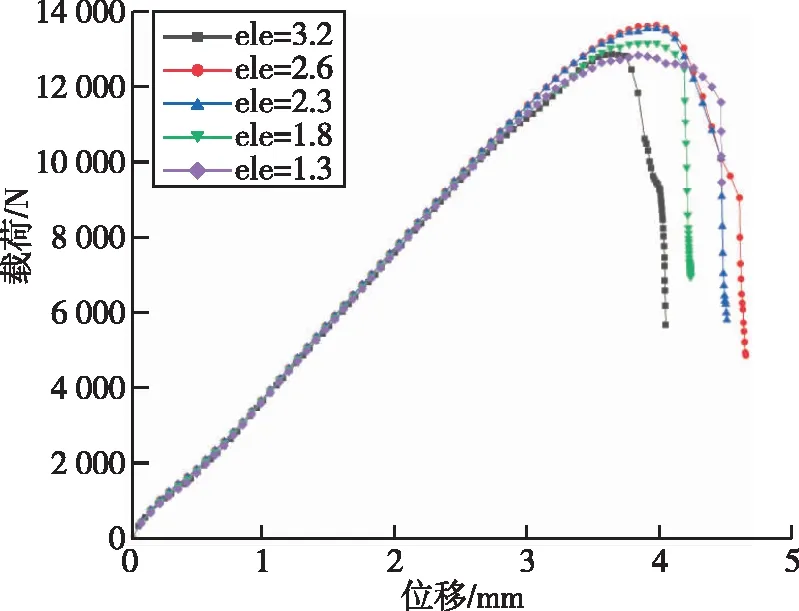
图11 不同网格密度下四点弯有限元模型的载荷-位移曲线

表 4为三横跨两筋条四点弯试验的失效载荷的对比，结果表明，在同样网格尺寸的情况下使用本文计算方法得出的失效载荷与试验结果相近，误差不超过14%，相较于开孔板试验的预测误差，预测四点弯试验产生较大误差的原因是在四点弯试验过程中层合板发生层间破坏，层合板产生了较大的翘曲，但由于子程序中无法获取变形曲率值，故利用该并行多尺度方法进行仿真模拟时，难以获取层合板的弯矩与曲率，导致预测结果比试验结果偏大。

表4 横跨两筋条四点弯试验失效载荷误差对比

3.4 网格相关性验证及计算效率对比

为检验本文所提出方法的网格相关性，在不同的网格密度下对所建立的有限元模型进行计算，所有有限元模型均通过网格相关性检验。图 11为四点弯有限元模型在不同网格密度下的载荷-位移曲线，其中ele为单元网格尺寸，单位为mm，该结果证明了本文所提出的方法不会因网格尺寸的变化而造成结果的较大变化。

本文对计算效率进行横向对于并予以评估，使用相同的计算内核数，对相同网格尺寸情况下并行多尺度方法耗时与内嵌Hashin损伤判定方法耗时进行对比，计算时间从每个算例的.msg文件中获取，评估结果如表 5所示，可得知，相较于使用FEA软件内嵌Hashin损伤判定方法，采用并行多尺度计算方法能够减少计算总耗时并且提高每一步计算的速度，能够缩短43%～85%的总计算时长，并且将每步计算效率提高1倍。

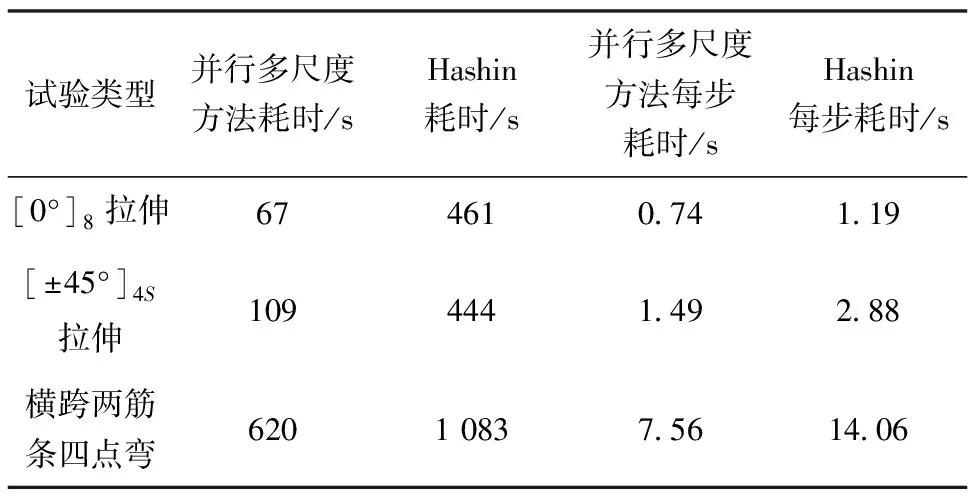
表5 计算效率对比

4 结束语

本文基于经典层合板理论通过建立层合板与层合板中每一层单层板的刚度矩阵，利用元软件分别对层合板、单层板两个尺度进行损伤判断。采用基于应力描述的最大应力准则、二维Puck失效准则以及Ye分层失效准则对每一层进行损伤初始判断。采用双线性渐进损伤模式对建立了复合材料层合板的损伤演化，并通过折减单层板的刚度反馈给层合板实现层合板的等效刚度折减，完成多尺度的损伤判断。

本文所使用并行多尺度计算方法通过T800级碳纤维增强复合材料开孔板拉伸试验以及横跨两筋条四点弯试验的算例验证，该方法进行了网格相关性检查，将仿真结果与试验结果进行对比。结果表明：通过该方法建立的模型能够较好地预测T800级碳纤维增强复合材料开孔板拉伸试验以及横跨两筋条四点弯试验的失效载荷，预测值与试验值平均误差低于10%；与使用内嵌Hashin损伤判定方法相比，该方法能够缩短43%～85%的总计算时长，并且将每步计算效率提高1倍；本文所使用并行多尺度方法受网格尺寸影响较小。