基于等几何方法的功能梯度Mindlin板结构拓扑优化设计

刘宏亮，姚力铭，王培金

(1.沈阳航空航天大学辽宁省飞行器复合材料结构分析与仿真重点实验室，沈阳 110136；2.大连理工大学工业装备结构分析国家重点实验室，大连 116023)

0 引言

随着高新技术的发展，飞行器通常需要在恶劣极端的环境下长时间工作[1]，对结构和材料性能的要求越来越高。由于比刚度和比强度等方面的优点，复合材料板在航空航天工业的应用愈发普遍。与传统的复合材料板不同，功能梯度复合板具有材料相之间平滑过渡且连续分布的特点，可以在很大程度上避免材料界面的出现对结构力学性能的影响，例如降低应力集中和减少残余应力。这实际上也是功能梯度结构相比传统复合材料结构的一个优势[2-3]。

在航空航天产品设计过程中，利用优化方法获得轻质高承载结构是实现装备轻量化和高性能化的一个重要且有效途径。相比尺寸和形状优化，结构拓扑优化的设计潜力更大，对结构的综合性能提升也更加明显，但同时其挑战性也更大[4-5]。目前，各种拓扑优化方法不断发展，例如变密度方法[6]、渐进结构优化方法[7]、水平集方法[8]、移动变形组件/孔洞方法[9-10]等。而且，相较于单相材料拓扑优化，考虑多相材料的结构拓扑优化研究近年来受到了更多的关注[11-13]。然而，多材料结构拓扑优化需要一个合适的优化模型，可以有效描述迭代过程中设计域内不同材料的分布，同时应该方便于设计优化过程的灵敏度分析计算[14-16]。

功能梯度结构的拓扑优化可以是单材料优化，也可以是多材料优化。当功能梯度结构的材料渐变方式确定时，只优化结构的拓扑构型属于单材料优化，例如，材料沿着厚度或者面内方向渐变且其分布确定的功能梯度板结构拓扑优化[17]。当梯度材料渐变与结构拓扑同步优化以实现功能梯度结构性能最优时，其本质上是一种多材料结构拓扑优化[18-19]。与传统多材料结构拓扑优化不同的是，这样的设计在材料相之间具有平滑且连续分布的特点。值得指出，现有的功能梯度结构拓扑优化研究主要考虑平面问题，尚未考虑工程中普遍存在的板结构设计。事实上，板结构的多材料拓扑优化设计研究也是近年来才受到关注[20-21]。因此，本文研究的重点是一种沿着面内方向材料渐变的功能梯度板结构拓扑与材料分布协同设计优化问题。

对于板结构的分析和设计，目前主要采用基于有限元方法的Kirchhoff板单元和Mindlin板单元。其中，Kirchhoff板单元适合薄板模型，而Mindlin板单元适合中厚板模型。薄板模型的适用范围有限，因此Mindlin板单元在工程中的应用范围更广。然而，Mindlin板单元进行有限元分析时可能会存在数值闭锁问题，严重影响数值计算的精度。为了实现更具工程应用性的板结构拓扑优化，克服数值求解难题，本文基于等几何分析[22]发展一种功能梯度Mindlin板结构的拓扑优化设计方法。采用具有高阶连续性的非均匀有理B样条(non-uniform rational B-spline，NURBS)基函数作为功能梯度板结构建模、分析和设计的基础，获得了梯度材料与结构拓扑协同优化设计方案。

1 功能梯度Mindlin板等几何拓扑优化设计

1.1 Mindlin板结构等几何分析

本文考虑的Mindlin板基于一阶剪切变形理论，假设板中面的法向纤维在变形过程中保持平直，长度不变，但不一定保持垂直于中面。因此，横向剪切变形不可忽略，Mindlin板的应变能由下式给出

(1)

式中，σf和εf是弯曲应力和应变，σc和εc是横向剪切应力和应变，α为剪切修正系数。线弹性应力应变关系可定义为

σf=Dfεf

σc=Dcεc

(2)

其中，Df和Dc分别表示弯曲项与剪切项的弹性常数矩阵，即

(3)

式中，E是弹性模量，ν是泊松比，G则是剪切模量。将式(2)和式(3)带入Mindlin板应变能式中可得

(4)

基于等几何分析，利用NURBS曲面表示结构的几何模型，即

(5)

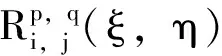
(6)

式中，Ni，p和Mj，q分别表示定义在节点矢量{ξ0，ξ1，…，ξm1}和{η0，η1，…，ηm1}上的B样条基函数，wi，j是控制点对应的权重系数。

在Mindlin板结构等几何分析中，NURBS基函数不仅用于结构几何模型的定义，同时也作为等参元的形函数。离散后的Mindlin板线弹性控制方程可表示为

KU=F

(7)

式中，U为位移矢量，K表示结构的整体刚度阵，它由单元刚度阵Ke组装而成，表示如下

(8)

式中，Bf和Bc分别为弯曲项和剪切项的应变位移矩阵，h表示板的厚度，ui，j为结构的位移场。

本文利用等几何分析的k细分方案可以实现NURBS基函数跨单元高阶的Cp-1次连续，在很大程度上可以缓解闭锁作用的影响。对于较薄的板模型，将采用NURBS等几何分析单元结合缩减积分的策略解决数值闭锁问题。

为了构建一个基于连续密度的梯度渐变结构优化问题，式(8)中的弹性系数矩阵近似为不同材料相的弹性常数，这将在下面讨论的插值方案中实现。

1.2 功能梯度拓扑优化的插值方案

在功能梯度结构中，材料之间不存在明确的界面，材料性能平滑变化。借鉴基于SIMP的变密度方法插值方案，假设板由两种材料构成，弹性模量分别为E1和E2，通过设计域内某一点上两种材料所占的百分比，即体积分数来表示这种连续变化材料的性质。

功能梯度材料性质的计算通常采用数值均匀化法和混合法。本文基于混合法，假设两种材料均匀混合，没有微观结构，如图1所示。目前，被广泛采用的几种混合模型包括Voigt模型、Halpin-Tsai复合模型、Voigt-Reuss界限和Hashin-Shtrikman界限[23]。本文研究重点是采用等几何方法实现优化设计，因此选择使用各向同性复合材料的Hashin-Shtrikman上界和下界的平均值作为材料模型。

图1 结构中某一点材料混合物

当两种材料的泊松比等于1/3时，Hashin-Shtrikam的上限和下限可简化为杨氏模量条件

(9)

当y→1时，Hashin-Shtrikam模型上下限均为E1，当y→0时，Hashin-Shtrikam模型上下限均为E2。假设E1>E2，当y=1时，此时结构中某一处全为强材料，当y=0时即为弱材料。当结构中一点是两种材料均匀混合时，采用Hashin-Shtrikam模型上下限均值近似表示为

(10)

借鉴SIMP方法，各向同性均质材料的性质被描述为E(x)=xpE0，设计变量为0时表示此处为优化所产生的孔洞。为了实现材料属性和结构拓扑的协同设计，功能梯度材料的插值模型被定义为

(11)

式中，p为惩罚系数。值得指出，对于式(11)中的设计变量y并不需要惩罚，因为设计目标是获得光滑渐变的功能梯度结构。为了避免数值奇异，插值格式中采用一个足够小的量纲为1的数Emin，即

(12)

1.3 功能梯度结构拓扑与材料协同优化列式

考虑体积约束下的功能梯度Mindlin板结构最小柔顺度优化问题，当功能梯度材料是由两种材料(例如金属与陶瓷)构成时，其对应的拓扑优化列式可以表示为

minimize:J(xi,yi)=FTU(xi,yi)

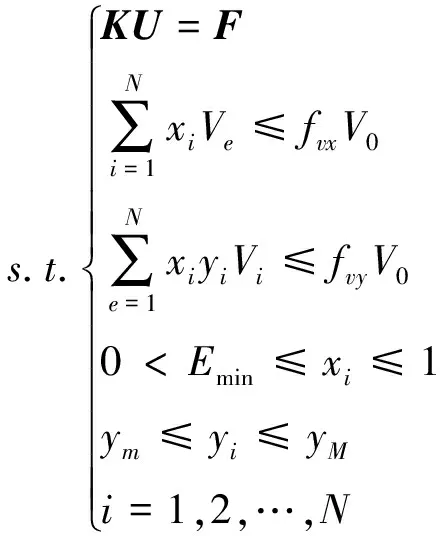
(13)

式中，J表示目标函数即结构的柔顺度，xi和yi表示控制点处的设计变量，分别对应总材料的体分比和强材料的体分比，Ve表示NURBS单元体积，V0表示结构总体积，fvx和fvy分别为材料用量的限制分数，即体积分数。fvx限制结构的总材料用量，fvy则控制有材料处的强材料占比。ym和yM为给定设计变量yi的上下限，由式(9)可知，若ym和yM取0和1则对应为Hashin-Shtrikam模型的上下限，为了保证实现强弱材料的光滑渐变，本文中ym和yM分别设置为0.1和0.9。

对于本文基于等几何方法的功能梯度Mindlin板结构拓扑优化，用于几何建模和结构分析的NURBS基函数也用于表示相对密度场，即

(14)

其中，Θ表示设计变量x和y组成的集合。由于NURBS基函数的非负性和规范性，当设计变量在给定的设计区间变化时，所对应的相对密度分布也会满足规定的区间分布，从而建立起合理的控制点密度设计变量和材料相对密度分布之间的映射关系。此外，NURBS基函数的高阶连续性可以避免棋盘格模式等数值问题[24]。

2 设计优化灵敏度分析

本文采用基于梯度的移动渐进线法[25](MMA)来更新设计变量，进而求解建立的优化列式(13)。这里需要计算目标函数和约束函数的灵敏度。功能梯度板的几何建模、结构分析和材料分布场采用统一的参数化，NURBS基函数的特性保证了解析灵敏度的有效计算。目标函数对于设计变量xe的灵敏度可表示为

(15)

式中单元刚度阵对设计变量xe的导数表达式为

(16)

根据链式求导法则可得到

(17)

式(17)中Mindlin板单元刚度阵由两项组成，分别为弯曲项与剪切项，则∂E/∂xe的计算表达式为

(18)

由式(15)和式(18)可得

(19)

目标函数对于设计变量ye的灵敏度表达式为

(20)

式中，∂Ke/∂ye可以参考式(16)和式(17)，而弹性模量对设计变量ye的一阶导数为

(21)

式中，E′(y)表示Hashin-Shtrikam界限对设计变量ye求导，可以表示为

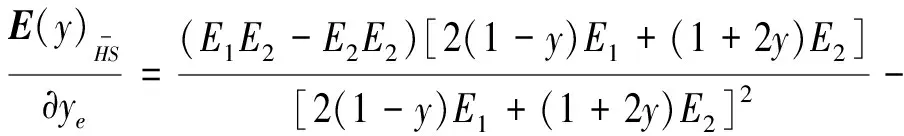
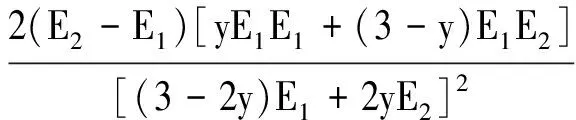
(22)

根据式(21)和式(22)可得

(23)

另外，体积约束的灵敏度可以直接求导得出。

3 数值算例与讨论

通过两个数值算例证明本文方法可以有效获得体积约束下的功能梯度Mindlin板结构拓扑优化设计。优化算例中采用二次NURBS基函数，为避免数值闭锁现象对Mindlin板结构等几何分析精度的影响，采用缩减的两点积分策略。剪切修正系数设置为α=5/6，材料用量限制比值为0.5。当连续两次迭代的目标值相对变化小于0.01或达到最大迭代次数50时，优化过程终止。算例中材料、几何以及载荷参数选择为量纲为1的参数。

3.1 四边固定的方板

第一个算例考虑一个四边固定的矩形方板(a×a=1×1)，在板中心处施加一个集中载荷(F=1)，如图2所示。板的厚度为0.1，参数设置参考了文献[20]，用红色表示强材料E1=4，蓝色表示弱材料E2=2，两种材料泊松比为0.3。总体积分数设为0.5，强材料体积分数占比V1从0.4下降到0.1，弱材料体积分数占比V2从0.1上升到0.4，J表示目标函数即柔顺度。将设计域细分为100×100的单元时，优化结果如图3所示。

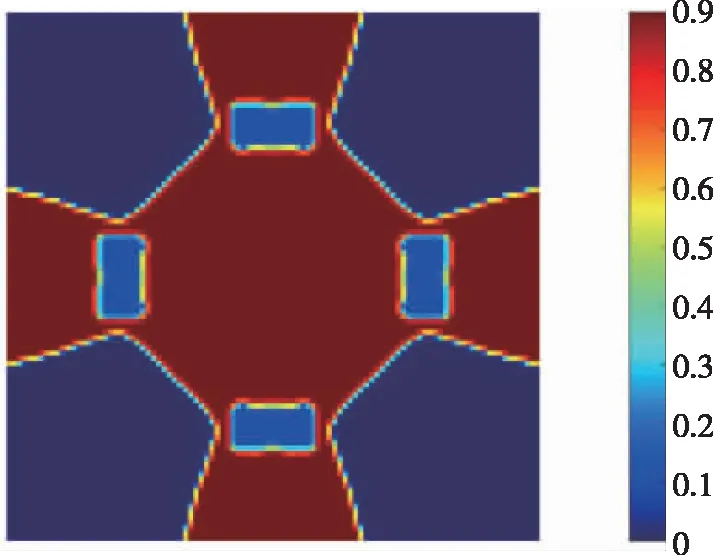
(a)V1=0.4，V2=0.1，J=30.52

在相同厚度和边界条件下，可以观察到材料填充面积与体积分数具有明显的相关性，随着硬质材料(红色)的体积分数逐渐下降，结构的柔顺度逐渐增加。可以推断出，在对结构刚度贡献较小的地方，软质材料倾向于替代硬质材料，而强材料总是分配在中心区域(集中载荷作用区)和应力集中区。4种不同强材料体积分数所对应的优化迭代曲线如图4所示。

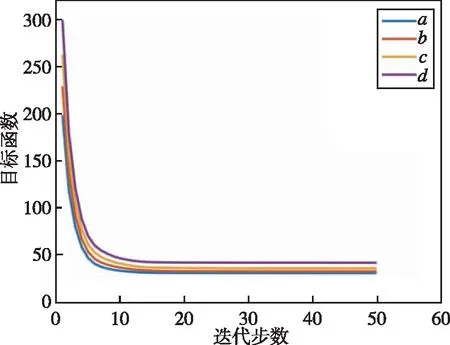
图4 4种不同强材料体积分数下的迭代曲线

图3中的4种优化结果，拓扑设计构型几乎一致，不同点在于材料分布，即强弱材料之间的过渡区域。图3右侧颜色栏中的0.1和0.9对应式(13)设定的Hashin-Shtrikam模型上下限。本文协同优化体现在两种设计变量分别控制结构拓扑与材料配比，如图5所示。右侧“0”表示结构中的孔洞，即图5黑白设计中的白材料。由于图3中可视化点的数量有限，功能梯度材料的渐变细节表示得并不是很清楚。由图4可知，其收敛速度较快，在20多步就已经收敛。在不改变设计优化计算效率的情况下，为了更清楚地显示梯度渐变细节，在图3优化结果的基础上，将用于描述最终优化结果的可视化点扩大100倍，如图6所示，可见优化结果具有清晰的拓扑设计和平滑的材料过渡区域。

图5 体积约束下的功能梯度板协同优化设计

(a)强材料体积分数为0.4

3.2 四边简支的方板

第2个算例考虑一个四边简支的矩形板，厚度为0.01，设计域参考图2，板的中心仍然施加一个集中载荷。强材料(红色相)的弹性模量E1=2，弱材料的弹性模量E2=1，两种材料泊松比为0.3，总体积分数为0.5，其中强材料占比为0.3。该算例的设计参考了文献[20]在多材料薄板拓扑优化设计中的算例。将设计域离散为50×50的单元，最终的优化结果如图7所示，目标函数的迭代曲线如图8所示。

(a)结构拓扑

图8 四边简支功能梯度板的迭代曲线

功能梯度结构拓扑优化设计也可以视作一种多材料结构拓扑优化设计，但是传统多材料结构拓扑设计的不同材料相之间存在明显的界面。图7(a)中的优化设计构型与参考文献[20]中单材料结构设计类似，但通过功能梯度材料结构协同设计优化，最终结构的目标函数值为137 319.91，在材料参数设置一致的情况下，结构性能优于参考文献中的双材料板拓扑优化设计，目标函数下降了11.28%，证明了本文设计方案的有效性和优越性。另外，可视化点的数量不依赖建模、分析和设计变量的数量，可以在保证功能梯度材料相之间连续且平滑渐变的同时兼顾设计优化的效率。

4 结束语

本文研究了一种在等几何分析框架下的功能梯度Mindlin板结构拓扑优化方法实现材料渐变分布与结构拓扑协同设计。采用基于NURBS的建模、分析和设计参数化方法来实现梯度材料结构的一体化优化设计。等几何方法中NURBS基函数用于梯度材料分布拓扑优化使得设计结果可以自然避免拓扑优化的常见数值不稳定问题，高阶连续性可以促进材料分布的光滑性以及设计优化的灵敏度分析，因此建立了合理的设计变量与材料分布的关系。数值算例表明，本文方法具有较好的收敛性，在不需要显著增加计算单元和设计参数的情况下能够有效获得具有清晰细节特征的结构拓扑与材料渐变的协同优化设计。通过与已有研究结果对比，本文优化设计方法展现了有效性和优越性。