平均信息年龄敏感的移动群智感知机制研究
2023-11-10肖明军
郑 俊,肖明军
1(中国科学技术大学 软件学院,江苏 苏州 215000)
2(中国科学技术大学 计算机科学与技术学院,合肥 230027)
3(中国科学技术大学 苏州高等研究院,江苏 苏州 215000)
1 引 言
随着移动互联网的迅猛发展,移动群智感知成为了一种极具吸引力的数据交互模式.典型的移动群智感知系统由一个部署在云上的平台和一些移动用户组成.通过云平台,数据需求者们可发布感知数据收集任务并雇佣移动用户完成感知任务.移动用户则使用手机、可穿戴设备等移动设备来手机感知数据并定期将数据传输给平台以换取报酬.
信息年龄定义为从该数据的最新版本产生时刻起到现在为止经过的时间.信息年龄是一种新颖的用来表征数据的新鲜程度或实时状态更新频率的评价指标.信息年龄追求的目标既不同于确保收到的数据更新具有最小的延迟,又不同于最大化通信系统的利用率.最大化通信系统的利用率只需要让移动用户尽快发送数据更新包,然而这会导致数据包积压在平台队列或通信链路中,从而导致数据更新延迟.
目前已有许多移动群智感知方向的研究工作,移动群智感知激励机制的相关研究是其中重要的一环,常见研究方案包括拍卖方案,博弈算法等.但是传统的移动群智感知激励机制设计大多致力于最优化参与方的经济效益,没有把信息新鲜度考虑在内或是作为优化目标.移动设备手机或产生的数据变化极快,为了保证移动群智感知系统收集的感知数据的可用性和有效性,需要保证这些数据的实时状态更新.因此,在移动群智感知系统中,确定每个移动用户向平台更新数据的频率就显得尤为重要.太慢的数据更新频率会导致数据被平台接受到时就已经过时,因此数据的信息年龄偏高.然而,因为移动群智感知系统是多个用户竞争向一个平台传输数据的系统,太快的数据更新频率会导致数据在平台处排队甚至是在链路中拥塞,导致实际上数据的信息年龄反而升高.因此,如何给每个移动用户确定一个适当的数据更新频率使得移动群智感知系统的数据的信息新鲜程度满足要求,是一个具有挑战性的问题.
为了解决上述挑战,本文提出了平均信息年龄敏感的移动群智感知机制设计.该机制的优化目标是推导出移动用户的平均信息年龄并保证其低于系统给定的阈值,以此来指导移动用户选择适当的数据更新频率.首先本文对移动群智感知系统进行建模并对数据新鲜度机制设计进行问题形式化.然后利用排队论知识,首先推导单个或多个同质的移动用户的移动群智感知系统的平均信息年龄表征.考虑了3种符合实际的先到先服务队列设置:到达率和处理率都服从泊松分布,或者到达率服从泊松分布而处理时间固定,或者到达率固定而处理率服从泊松分布,并分别推导出相应的平均信息年龄表达式.以此作为基础,本文进一步推导出多个同质的移动用户的移动群智感知系统的平均信息年龄表征,进而给出了信息新鲜度阈值限定下,移动用户可选的数据更新频率范围.
2 相关工作
移动群智感知是学术研究中热门且经典的研究方向.在这个领域有相当多的研究工作[1].例如Zhang等人基于在线反向拍卖设计了3种在线激励机制[2],实现了平台效益最大化和保证了拍卖的诚实性.Yang等人针对以平台为中心的系统设计了一个基于斯塔尔伯格博弈的激励机制[3],而面对以用户为中心的系统则转而采用了基于拍卖的激励机制.Song等人设计了一个激励机制用于解决工人选择问题[4],通过将任务分配问题建模成一个组合多臂老虎机模型,该机制能最小化工人结果的经验熵.然而,这些现存的工作都只考虑了最大化效益的问题,没有将信息新鲜度(AgeofInformation,AoI)纳入考虑范畴.而随着移动互联网的发展,对信息新鲜度的要求也与日俱增.因此现有的工作无法解决优化目标中涉及到信息新鲜度的激励机制设计问题.
AoI是一个被广泛使用的评判信息新鲜度的标准.AoI是指从最新的信息产生依赖经过的时间.在近些年有大量AoI领域的研究工作[5-7].AoI领域的博弈论相关工作主要研究如何最小化AoI花销[8-12].然而,大多数研究工作没有跟迅猛发展的移动群智感知相结合.而且,为了简化工作,他们通常不区分不同的移动用户,从而将AoI排队系统视为单源排队系统.相比之下,本文的工作同时考虑了多同质移动用户和多异质移动用户竞争的排队论系统,更符合实际情况.
3 模型总览
移动群智感知系统的整体流程如图1所示并可以具体描述如下:首先,平台向移动用户发布感知任务,感兴趣并乐意参与的N个移动用户做出回应.其次,平台决定自己的报价策略,移动用户决定自己的数据传输频率策略.再次,移动用户以一定频率向平台传输感知数据.平台持续更新聚合数据并进行分析,并向每个用户支付基于报价策略的报酬.
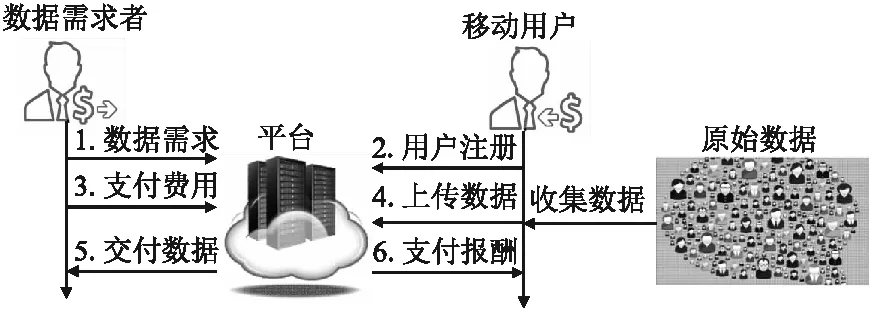
图1 系统总体结构图Fig.1 System overview
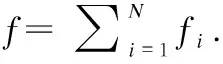
4 单(多同质)移动用户的信息新鲜度研
本章通过分析信息年龄曲线来推导出单个移动用户或者多个同质移动用户时平均信息年龄的表达式.多个同质移动用户是指多个移动用户的数据包很相似,平台在处理和排队时不加以特定区分,一起排队处理,仅计数并在结算时加以区分,因此可以将系统等价为只有一个移动用户的排队系统.信息年龄的示例曲线如图2所示.
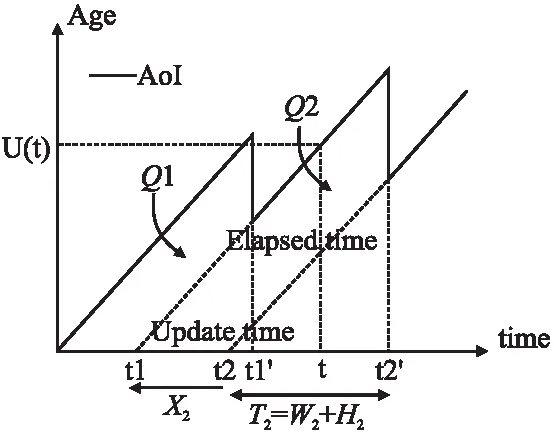
图2 信息新鲜度示意图Fig.2 Example of AoI
因为AoI是从最新收到数据包的产生时间开始计算,它实际上包含了链路传输时间、到达平台后在队列中的等待时间等.因此AoI曲线会随着时间线性增加并在接收到一个新的数据包后断崖式下跌,最终呈现一个锯齿形.
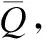
(1)
从图2中可以看出,区域Qi可以被表示为相邻两个等腰直角三角形的面积差.定义Xi为数据包i-1和数据包i的生成时间之间的差值,即Xi=ti-ti-1.则Qi可以被表示为:
(2)
将式(2)代入式(1)中,平均AoI可以被重写为:
(3)
(4)
则f1正是该移动用户的数据更新频率,显然其极限是存在的.则可以重写平均AoI如下:
(5)
式(5)中E[.]是期望运算符,X和T分给是与链路传输时间和平台处理时间对应的随机变量.并且式中平均AoI的计算基于系统服务遍历性的弱假设,即该系统需要遍历所有数据包而不允许随意丢弃任何数据包.该式是先到先服务队列系统中处理AoI相关问题的常规性推导结果.然而,要进一步推导计算平均AoI依然是一个极具挑战性的任务.首先考虑一种特殊情况,X是系统当前数据包和上一个数据包的生成时间的差值的随机变量,而T是描述上述两个数据包的系统时间的随机变量.这种假设情况下X与T是相互独立的随机变量,问题得到简化并很容易求解.然而实际情况更为复杂,当时间间隔X很大时,意味着系统队列是空的,此时将产生一小段等待时间和系统时间T.这种情况下的X与T是不再是相互独立的随机变量,而是负相关的,这使得E[XT]的计算变得复杂很多.
4.1 M/M/1队列的信息新鲜度研究
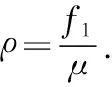
对于数据更新包i而言,其系统时间可以表示如下:
Ti=Wi+Hi
(6)
式(6)中Wi和Hi分别表示数据更新包i的等待时间和处理时间.接下来分两种情况讨论:第1种情况是当数据更新包i产生时,数据更新包i-1已经被平台处理完成,此时Wi=0;第2种情况是数据更新包i产生时刻,数据更新包i-1正在系统队列中排队等待处理或者正在被处理,此时Wi=Ti-1-Xi.综合考虑这两种情况,可以将数据更新包i的等待时间Wi重写如下:
Wi=(Ti-1-Xi)+
(7)
注意到Ti-1独立于Xi.当系统处于稳定状态时,系统时间T是随机同分布的,即T=Ti=Ti-1.由排队论知识可推导出,M/M/1系统中系统时间T的概率密度函数为:
fT(t)=μ(1-ρ)e-μ(1-ρ)t,t≥0
(8)
则给定Xi=x条件下等待时间Wi的期望值可以表示如下:
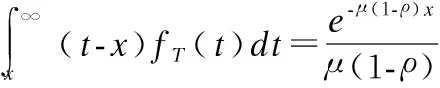
(9)
因此,注意到处理时间Hi独立于Xi,这允许重写E[XT]=E[XiTi]如下:
E[TiXi]=E[(Wi+Hi)Xi]=E[WiXi]+E[Hi]E[Xi]
(10)
(11)

(12)
4.2 M/D/1队列的信息新鲜度研究
本章节考虑M/D/1队列系统,该系统中移动用户的数据包到达服从泊松分布,但平台的服务时间是固定的.这个设定也比较符合移动群智感知系统中平台的实际情况,因为在同一个感知任务中,平台将任务分发给不同的移动用户去完成,最终从不同移动用户处收集的感知数据的形式、大小、内容分布等较为相似,因此平台可以在固定的服务时间内完成处理.
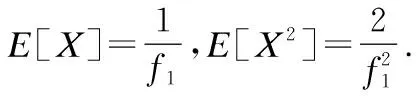
Ti=Wi+C
(13)
其中Wi和C分别表示数据更新包i的等待时间和处理时间.于是有式子如下:
E[XiTi]=E[XiWi]+DE[Xi]
(14)
类似公式(9),可推导出式子如下:

(15)
其中,有阶跃函数如下:
(16)
于是可以求得:
(17)
概率密度函数fY(y)对应的概率分布函数为:
(18)
同理,将公式(18)代入公式(15)中,可得E[Wi∣Xi=x],再代入公式(11)中,可求得E[WiXi].将E[WiXi]代入公式(5)中,最终可求得平均信息年龄δ.
4.3 D/M/1队列的信息新鲜度研究

(19)
E[XT]=CE[T]
(20)
将公式(19)、公式(20)代入公式(5)中,可以重写公式(5)如下:
(21)
而平均的系统时间可以表述为式子如下:
(22)
其中:
γ=LX(μ(1-β))
(23)
是到达时间间隔的拉普拉斯变换的解.而此处到达时间间隔固定为C,因此有公式如下:
fX(x)=ε(x-C)
(24)
LX(t)=e-tC
(25)
于是可以重写γ表达式如下:
(26)
(27)
5 多异构移动用户竞争的信息新鲜度研究
本章将上述单个或者多个同质移动用户队列系统的平均AoI推广到多异质移动用户竞争的情形下.此处异质指移动用户的数据包各不相同,平台排队时需加以区分处理.
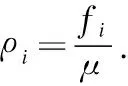
令T=W+H,此处W和H分别代表系统中所有等待时间和处理时间.H独立于X,则有:
E(XT)=E(XW)+E(X)E(H)
(28)
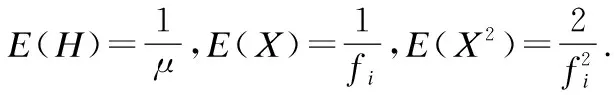
(29)
然而,E(XW)的计算是非平凡的,因为X和W并不是相互独立的而是负相关的.因为当到达间隔时间X较大时,意味着多工人竞争的队列系统仍然可能为空,此时会产生额外的一段等待时间并被记为W.因此问题求解的关键转化为如何求解该非平凡的E(XW).而要求解E(XW)需要用到指数型随机变量和泊松过程的相关性质,具体如下.
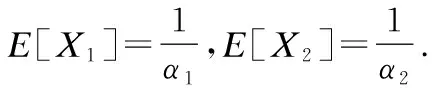
2.给定X1 fX1∣X1 (30) 引理2.对于给定的速率为f1的泊松过程N(t),和一个与其独立的指数型随机变量X,在[0,X]区间内的到达数N(X) 的概率质量函数PN(X)(n)可表示如下: PN(X)(n)=(1-γ)γn,n≥0 (31) 这两个引理的证明较为容易,此处不在赘述. 要设法求得该非平凡的E(XW),令Xj,Wj和Tj分别表示移动用户i的数据包j的到达时间间隔,等待时间及系统时间.于是可以将Wj划分为如下两个区间: Aj={Xj (32) 区间Aj意味着移动用户i的数据包j的到达时间间隔比较短,具体来说是短于该系统处理移动用户i的数据包j-1的系统时间.而区间Gj则正好相反,表明移动用户i的数据包j的到达时间间隔较长,长于该系统处理移动用户i的数据包j-1的系统时间.于是,通过划分为两个区间,可以将E(XW)重写如下: E(XjWj)=E(XjWj|Gj)P[Gj]+E(XjWj|Aj)P[Aj] (33) 因为该排队系统只有一个用于服务的平台,所以移动用户i的数据包与其他所有移动用户的数据包被平台处理所需的处理时间都是相同的指数型随机变量μ.与单个用户或者多个同质用户的队列系统排比,该多移动用户的队列系统仍然是M/M/1先到先服务队列系统,只是系统的总负载率变为了ρ=ρi+ρ-i.当该排队系统处于稳定状态时,系统时间Tj-1的指数为μ-f的概率密度函数可表示如下: fT(t)=(μ-f)e-(μ-f)t,t≥0 (34) 此外,系统时间Tj-1与Xj是相互独立的,因为Tj-1取决于第j-2个数据包的处理时间.于是,分两种情况讨论推导后,可得出多异质用户移动群智感知系统的平均AoI表示成定理形式如下. (35) 本章节中,使用实验仿真来详细评估了单(多同质)和多异质移动用户情形下的的平均信息年龄表征情况,表明了其正确性和合理性. 我们采用芝加哥出租车开源数据[13]作为真实数据集来进行实验仿真.每一份数据都记录了taxiID,timestamp,trip_miles,trip_seconds及顾客上下车地点等.我们从该开源数据库中选择了一个27030条数据的数据集.在实验仿真中,我们将其看成移动群智感知应用场景,将司机接送乘客看做完成相应的群智感知任务.乘客上下出租车地点看做群智感知中收集数据的兴趣点(PoI).首先,我们选择L=15个PoI并找到对应的数据库中的300条出租车行程记录.其中我们可以选择N个出租车和M个相应的感知任务.其中N的取值范围是[50,300],默认值为100.不失一般性,该数据集中缺失的少量符合随机分布的数据我们使用高斯分布来生成. 首先,分别观察单(多同质)移动用户时,M/M/1,M/D/1,D/M/1这3种先到先服务队列情形下,改变系统负载率ρ时,平均AoI的变换情况,如图3所示.随着系统负载率ρ的增大,3幅曲线的平均AoI都是先减小后增大,存在唯一的最小值.通过具体观察可知,M/M/1队列中平均信息年龄取最小值时ρ≈0.53.M/D/1队列中平均信息年龄取最小值时ρ≈0.625.D/M/1队列中平均信息年龄取最小值时ρ≈0.515.因此,当系统设定一定的信息新鲜度阈值时,只有中间特定范围内的ρ满足系统的信息新鲜度阈值需求. 图3 单用户不同队列AoI图Fig.3 AoI of single user and different queue 首先测量先到先服务的队列系统的平均AoI.为了简化问题和结果的直观性,假定只存在两个移动用户竞争更新数据,有ρ1+ρ2=ρ. 从图4(a)可以得出,一个移动用户的数据的平均AoI随着另一个用户的AoI的减少而增加.而对于不同的总和ρ而言,与ρ=0.4,0.7,0.8相比,当ρ=0.6时,AoI的总和最小.因此,可以通过调整总和ρ来尽量减小AoI总和,从而保证不超过AoI阈值,使AoI约束得以生效. 图4 两竞争用户AoI图Fig.4 AoI of two competitive users 从图4(b)可以得出,随着总负载ρ的增加,用户1的AoI逐渐减小,用户2的AoI逐渐增大,而总AoI先减小后增大,因此AoI总和存在最小值.而对于对称情况,最小值当用户1和用户2的AoI相等时取得.因此可以得出通用性结论:对于多用户系统,AoI阈值约束问题既取悦于总负载ρ,又取决于移动用户间数据更新频率的分配关系,且平均AoI存在唯一的最优值. 综合上述所有数据图,可以进一步论证本文建模推导的单(多同质)和多异质移动用户的信息新鲜度表征的正确性和合理性. 本文研究了平均信息年龄敏感的移动群智感知机制设计问题.本文首先给出了移动群智感知中的平均信息年龄的建模和问题形式化.然后逐步推进,先研究了单个或者多个同质用户情形下的平均信息年龄设计问题,并考虑了3种常见的队列设置来分别推导其结果.以此作为前提,进一步推导出更符合实际情况的多个异质移动用户情形下的非平凡的平均信息年龄设计问题,通过一系列复杂的推导过程最终得到表征式.然后,数值结果的评估结果论证了所设计的所有移动群智感知系统的平均信息年龄的正确性和合理性.未来的工作包括将队列拓展到后到先服务等其他队列系统,或者同时考虑系统的经济效益和信息新鲜度问题以达到一种平衡.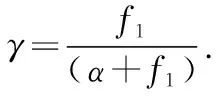

6 实验评估
6.1 实验环境配置
6.2 单(多同质)移动用户AoI的评估结果
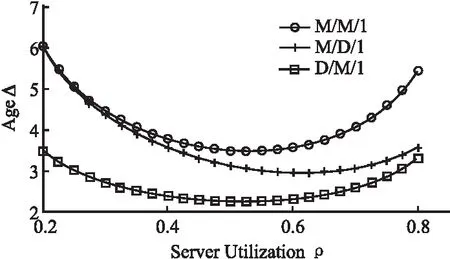
6.3 多异质移动用户AoI的评估结果

7 结 语
