径向基函数神经网络指导的粒子群优化算法求解多峰优化问题
2023-11-11张潇,宋威,2
张 潇,宋 威,2
1(江南大学 人工智能与计算机学院,江苏 无锡 214122)
2(江南大学 江苏省模式识别与计算智能工程实验室,江苏 无锡 214122)
1 引 言
粒子群优化(Particle Swarm Optimization,PSO)[1]算法一种典型的群体智能(Swarm Intelligence,SI)[2]算法,它模拟了自然界中生物种群的自组织交互行为,具有对问题解析性质要求低,实现简单且收敛速度快等优点.在过去20年间PSO受到学术界的广泛关注,并被应用于特征选择[3]、人群分类[4]、车间调度[5]和疫情传播预测[6]等多种领域.然而,在现实世界中存在着大量多峰优化问题.该类问题的特点是,在解空间中同时存在着多个局部最优解与一个全局最优解.利用传统PSO算法求解多峰优化问题时,由于缺乏多样性且搜索动作选取不合理,导致其难以找到问题的全局最优解.
目前,一些PSO的改进方法将种群划分成多个子群,其目的是保持种群多样性[7,8].然而这些方法大多依赖于人为经验或是预设的规则,根据各粒子在解空间中的位置,利用聚类或小生境的思想将整个种群划分为多个子群,使各子群分布在解空间中的不同区域来进行搜索.Kennedy最早提出利用PSO算法来求解多峰优化问题[9],其思路是利用k-means算法将种群聚成多个类簇,然后用类簇的中心作为该邻域的最优解,指导对应类簇中粒子的学习.Brits等人提出了一种基于小生境技术的PSO算法[10],具体内容包括:如果主种群中某个粒子的适应值在一定的迭代次数中变化较小,该粒子将和当前主种群中距其最近的另一个粒子构成一个小生境.此过程不断循环,最终实现子群的划分.Parrott等人提出了一种基于种群生成的PSO算法[11],在运行的每一代,首先将当前种群中适应值最优的粒子确定为一个种子,并利用该种子和空间中所有与它距离小于一定半径的粒子来构造一个种群.剩余的粒子会重复上述构造过程,直到全部粒子均被划分至不同的种群,因而使得不同种群将在不同的区域进行搜索.然而,上述的多子群方法需要与问题相关的先验知识,如预先设置聚类簇的个数或种群半径等,导致这些方法无法根据不同的优化问题合理地划分子群.而且这些方法也没有对粒子的搜索动作进行精心地设计,影响了搜索的性能.针对上述问题,本文将径向基函数神经网络引入PSO,提出一种径向基函数神经网络指导的粒子群优化(Radical Basis Function Neural Network Guided Particle Swarm Optimization,RBFNN-PSO)算法来求解多峰优化问题,RBFNN-PSO利用径向基函数指导网络(RBF Guided Network,RBFGN),在保持种群多样性的前提下,对包括定位学习目标和调整加速系数在内的搜索动作进行合理的指导.
为了在搜索过程中保持种群多样性,首先设计子群划分方法,选择能代表子群的搜索特性且与现有子群中心远离的粒子作为子群中心.子群的搜索特性通过候选子群中心对由其确定的子群中所有粒子的重要性进行体现.所设计的子群划分方法通过选择合适的子群中心,实现子群的划分.因此,不同子群中的粒子在各自子群中心指导下搜索,呈现出多样的搜索特性,提升了种群多样性.其次,在考虑多样性的同时,选择各子群中心作为相应子群中粒子的学习目标,实现了粒子学习目标的定位.由于将粒子当前位置映射为搜索动作属于非线性映射,作为典型的非线性映射模型,本文利用径向基函数神经网络,实现从粒子位置到搜索动作的映射.同时,径向基函数神经网络属于增量模型,能利用输入的每个位置来更新网络.本文设计RBFGN的输入为种群中每个粒子的当前位置,之后利用获取的子群中心设置其隐藏层节点.为了调整粒子的加速系数,在RBFGN输出层输出当前输入粒子的加速系数调整动作,包括增加、减少加速系数或保持加速系数不变3个动作.最后,为了训练RBFGN,本文引入强化学习对网络决策出的动作(包括定位学习目标和调整加速系数)进行奖励或惩罚,其目的是根据反馈,获得最大的累积收益,实现对隐藏层节点(代表子群中粒子的学习目标)和输出动作相连权值(控制粒子的加速系数)的有效调整,从而使RBFNN-PSO能合理指导粒子的搜索动作,以解决多峰优化问题.
2 相关工作
2.1 粒子群优化算法
PSO由Kennedy和Eberhart于1995年提出,它通过模拟鸟群觅食行为来寻找问题的最优解.具体而言,PSO中每个粒子具有速度和位置两种属性,根据自身和种群的历史最优位置来确定下一步搜索动作.带有惯性权重的标准PSO由Shi和Eberhart在1998年提出.每次迭代中,第i个粒子的速度和位置更新公式如下:
vi(t+1)=w×vi(t)+c1×r1×(pbesti-xi(t))
+c2×r2×(gbest-x(t))
(1)
xi(t+1)=xi(t)+vi(t+1)
(2)
其中,xi(t)表示第i个粒子在第t次迭代的位置,vi(t)表示第i个粒子在第t次迭代的速度,pbesti表示第i个粒子历史最优位置,gbest表示种群的历史最优位置.c1和c2代表两个加速系数,r1和r2是[0,1]范围内均匀分布的两个随机数.w是惯性权重,用于控制各粒子上一代速度对当前速度的影响.目前通用的惯性权重控制方法是使其随着迭代次数的增加而线性减小[12]:
(3)
其中,wmax为迭代开始时最大的惯性权重值,wmin为迭代结束时最小的惯性权重值,Tmax表示最大迭代次数.
2.2 径向基函数神经网络
径向基函数神经网络(Radical Basis Function Neural Network,RBFNN)于1988 年由Broomhead和Lowe提出.它属于前馈型神经网络,具有良好的泛化能力与较快的收敛速度,能以较高的精度逼近任意函数,常用于拟合难以解析的非线性映射[13].RBFNN输入层与隐藏层之间的连接仅起到传输数据的功能,因此前两层间的权值均为1.隐藏层激活函数为径向基函数,通常选用高斯核函数,高斯核函数包含中心μ与宽度σ两个属性,第k个隐藏层节点对于第i个输入xi的激活结果为:
(4)

(5)
其中,αk是第k个隐藏层节点与输出层相连的权值向量.
3 RBFNN-PSO算法
3.1 径向基函数指导网络RBFGN
本文设计RBFGN,其目的是获取一种不依赖于先验知识便可解决多峰优化问题的方法,RBFGN通过提升种群多样性并合理指导粒子的搜索动作来有效求解多峰优化问题.由于需要将输入的粒子位置映射为其对应的搜索动作,此过程属于非线性映射.作为典型的非线性映射模型,本文基于径向基函数神经网络,进一步设计RBFGN,实现从粒子位置到其搜索动作的映射,以更好解决多峰优化问题.
本文构造的RBFGN包含输入层、隐藏层和输出层,是一个紧凑的3层径向基函数神经网络.RBFGN的输入为种群中每个粒子的当前位置,因此,RBFGN的输入层包含D个节点,对应粒子位置在空间中的D个维度.输入层与隐藏层之间的连接仅起到传输数据的功能,因此前两层间的权值均为1.RBFGN的隐藏层包含若干个节点,每个节点代表一个子群,RBFGN通过调整隐藏层节点,实现对种群的划分.隐藏层节点的中心μ与宽度σ对应相应子群的子群中心与子群宽度.为了使初始子群分布在解空间中的不同区域,本文利用层次的k-means聚类方法来初始化子群.首先将种群中的粒子划分为l×k个类簇,由于种群规模(N=50)的限制,取l为2.随后每两个最相近的类簇将会融合,直到最后只剩下k个类簇,将k个类簇的中心作为初始的子群中心,每个类簇中所有粒子到中心的平均距离作为初始的子群宽度.受限于种群规模(N=50),初始的子群个数k设置为10,对应初始的10个隐藏层节点.
在初始化RBFGN隐藏层节点之后,第i个输入粒子xi经过第k个隐藏层节点利用公式(4)进行激活,输出的响应为φk(xi).同时,由公式(4)可以看出,若xi离某个子群中心μk的距离大于子群半径σk,它将会得到较小的响应.因此,xi受其最近子群中心的影响最大,该粒子将被分配到其最近子群中心所确定的子群中,并向该中心学习.RBFGN输出层包含3个节点,分别代表3个候选动作,即增加、减少局部加速系数cn或保持cn不变,其中cn控制着xi向其子群中心学习的力度.根据公式(5),拥有m个隐藏层节点的RBFGN输出为zi.为了便于后续的网络训练,本文利用softmax来激活zi,将其归一化到[0,1]区间:
oi=softmax(zi)
(6)
其中,oi⊆3表示zi经过激活后的结果.在3个输出节点中,产生最大输出值的节点将被选为动作节点,其输出值yac为:
yac=max(oi)
(7)
然后,RBFGN根据选择的动作节点来更新cn:
(8)
其中,Δ代表加速系数cn的变化.公式(8)中的3种情况分别对应3种候选动作,即增加、减少cn或保持cn不变.随后给出粒子的全局加速系数:
cg=c-cn
(9)
其中c=4.0为常数,这是由于大量的实验已证明将加速系数之和设置为4.0有利于粒子群优化算法找到最优解[14,15].同时,cn和cg的初始值均设置为2.0,以在算法初始阶段平衡局部与全局搜索.根据公式(8)和公式(9)获得的cn和cg,进一步给出当前输入粒子xi(t)的速度和位置更新公式:
vi(t+1)=w×vi+cg×rg×(gbest-xi(t))
+cn×rn×(μnr-xi(t))
(10)
xi(t+1)=xi(t)+vi(t+1)
(11)
其中,t与t+1是连续的两个时刻,w代表惯性权重,μnr表示离xi(t)最近的子群中心,gbest为全局最优位置,rg和rn是两个[0,1]范围内均匀分布的随机数.本文利用RBFGN来定位每个输入粒子的学习目标,并调整其局部加速系数.进一步地,利用公式(10)和公式(11)实现粒子位置的更新,并评价其在新位置的适应值.从而构造出RBFNN-PSO.图1给出了的RBFNN-PSO的结构图.

图1 RBFNN-PSO结构图Fig.1 Structure of RBFNN-PSO
3.2 子群候选中心的重要性
RBFGN通过调整代表子群的隐藏层节点,实现种群的划分,以生成多个子群.RBFGN隐藏层节点包括中心μ与宽度σ对应相应子群的子群中心与子群宽度.之后,SBDNN为每个输入粒子选择离其最近的子群中心作为学习目标.为保持种群的多样性,首先需要选出能反映子群搜索特性的候选中心,子群的搜索特性通过候选中心对由其确定的子群中所有粒子的重要性进行体现.具体地,候选中心的重要性定义为其所属隐藏层节点在网络输出上做出的平均贡献,该贡献利用移除其所属隐藏层节点后对网络输出造成的误差来计算.例如,对于输入粒子xi,若候选中心属于第j个隐藏层节点,则当第j个隐藏层节点被移除时剩余m-1个隐藏层节点的网络输出为:
(12)
根据公式(5)和公式(12),移除第j个隐藏层节点对网络输出造成的误差为:
(13)
因此,候选中心中重要性sj由移除其所属的第j个隐藏层节点后,对网络输出造成的平均误差来计算:
(14)
其中,p为候选中心所属的第j个隐藏层节点对应子群中粒子的个数.通过计算候选中心所属隐藏层节点的贡献,从而获得候选中心的重要性.
3.3 增加子群(隐藏层节点)
随着种群中粒子的顺序输入,如果某个输入粒子的重要性足够高,那么它便能反映由其确定子群的搜索特性,并将作为其确定子群的候选中心.为保持种群多样性,还需考虑该候选中心是否和已有的其他中心相近.因此,根据候选中心的重要性,以及该中心与已有的最近子群中心的距离,设计增加子群的条件:
(15)
其中,xi代表当前输入网络的粒子,xj代表将被划分到以xi为中心的新子群中的粒子,p代表将要被划分到新子群中粒子的个数.μnr代表离xi最近的已有子群中心,ε和σmin分别代表重要性阈值和距离阈值.因此,当两个条件均满足时,xi将作为其确定子群的中心.由于不同子群的中心相互远离,且不同子群中的粒子分别向能反映各自子群搜索特性的中心学习,整个种群将呈现多样的搜索特性,提升了种群的多样性.相应地,新增加的第m+1个隐藏层节点的中心位置μK+1,宽度σK+1,以及该节点与输出层节点相连的权值αK+1被初始化为:
(16)
其中,κ是重叠因子,它决定搜索空间中新子群与其最近子群间的重叠程度,为了实现子群的公平划分,κ设置为0.5.ei设置为di-zi,其中zi和di分别为网络在增加隐藏层节点前对于输入粒子xi的实际输出与期望输出,其目的是使网络在增加隐藏层节点后,针对输入粒子xi能做出期望的输出.
3.4 基于强化学习的网络训练
本文引入强化学习来训练RBFGN.具体地,通过对网络决策出的动作进行奖励或惩罚,并根据产生的反馈来训练网络参数.期望利用反馈,获得最大的累积收益,实现对隐藏层节点(代表子群中粒子的学习目标),以及其与动作节点相连权值(控制粒子的加速系数)的有效调整.对于输入的粒子,在经过网络决策出的动作指导其学习之后,若其适应值变好,则动作节点将收到正反馈,即奖励;反之,它将收到负反馈,即惩罚.
对于输入到RBFGN的粒子xi,根据公式(15)若增加子群的条件均满足时,xi将作为新的隐藏层节点中心,亦被看作是新的子群中心.相应地,新的隐藏层节点中心、宽度,以及该节点与输出层节点相连的权值将按照公式(16)进行设置.否则,若公式(15)的任一条件不满足,xi将被考虑用于更新RBFGN.在此情况下,针对RBFGN隐藏层节点和权值的更新,只需考虑更新距xi最近的子群中心、该中心所在隐藏层节点的宽度,以及该中心所在隐藏层节点与动作节点相连的一个权值.这是因为:1)本文利用梯度下降法来更新网络参数,由公式(4)可知,当隐藏层节点的中心离xi较远时,该节点将产生较小的响应,而且相比于产生的响应,该节点响应的一阶导数会更快地趋近于0.因此在网络隐藏层节点更新方面,只需更新距xi最近的子群中心,以及该中心所在隐藏层节点的宽度;2)在输出层中,利用强化学习只奖励或惩罚拥有最大输出的动作节点.因此在网络权值更新方面,只需更新距xi最近子群中心所在隐藏层节点与动作节点相连的一个权值.
具体地,对于输入的粒子,在经过网络决策出的动作指导其学习之后,若其适应值变好,此时将对动作节点进行奖励,使其输出趋近于1.反之,若其适应值变差,则需对动作节进行惩罚,使其输出趋近于0.基于梯度下降法,给出RBFGN权值的更新:
Δαac=ηzac(dac-yac)yac(1-yac)
(17)
αac=αac+Δαac
(18)
其中αac代表距xi最近子群中心所在隐藏层节点与动作节点相连的权值,Δαac代表权值的更新梯度,η代表学习率.zac代表动作节点在softmax操作之前的实际输出,yac代表动作节点在softmax之后的实际输出.dac是动作节点在softmax之后的期望输出,即当动作节点受到奖励时dac为1,否则dac为0.
在更新权值之后,继续更新距xi最近的子群中心μnr,以及该中心所在隐藏层节点的宽度σnr.在公式(17)中已得到(dac-yi)yi(1-yi)的结果,故不需再重复计算,设qac=(dac-yi)yi(1-yi),则μnr和σnr的更新如下:
(19)
μnr=μnr+Δμnr
(20)
(21)
σnr=σnr+Δσnr
(22)
其中,Δμnr和Δσnr分别代表μnr和σnr的更新梯度.
3.5 删除子群(隐藏层节点)
随着种群的进化与网络的更新,粒子的位置不断发生改变,而且包含子群中心的隐藏层节点也会被更新,针对输入到RBFGN的粒子xi,若离其最近的子群中心k无法反映所属子群的搜索特性,或者该子群中心与其他子群中心距离较近,则需考虑删除该子群,故删除子群的条件为:
(23)
其中,xj代表由第k个子群中心所确定子群中的粒子,p是该子群中粒子的总数,μk和μnr分别代表第k个子群中心的位置和距该中心最近的另一子群中心的位置.ε和σmin分别代表重要性阈值和距离阈值,这两个阈值被同样地用于公式(15).基于公式(16)中的重叠因子k=0.5,公式(15)和公式(23)中σmin设置为当前隐藏层所包含的最小子群宽度的两倍,以确保每个隐藏层节点的子群宽度至少为当前最小的子群宽度.若公式(23)的任一条件被满足,将删除离xi最近的子群中心k所在的子群(隐藏层节点).
3.6 算法流程
RBFNN-PSO的流程图如图2所示,RBFNN-PSO的算法步骤见算法1.
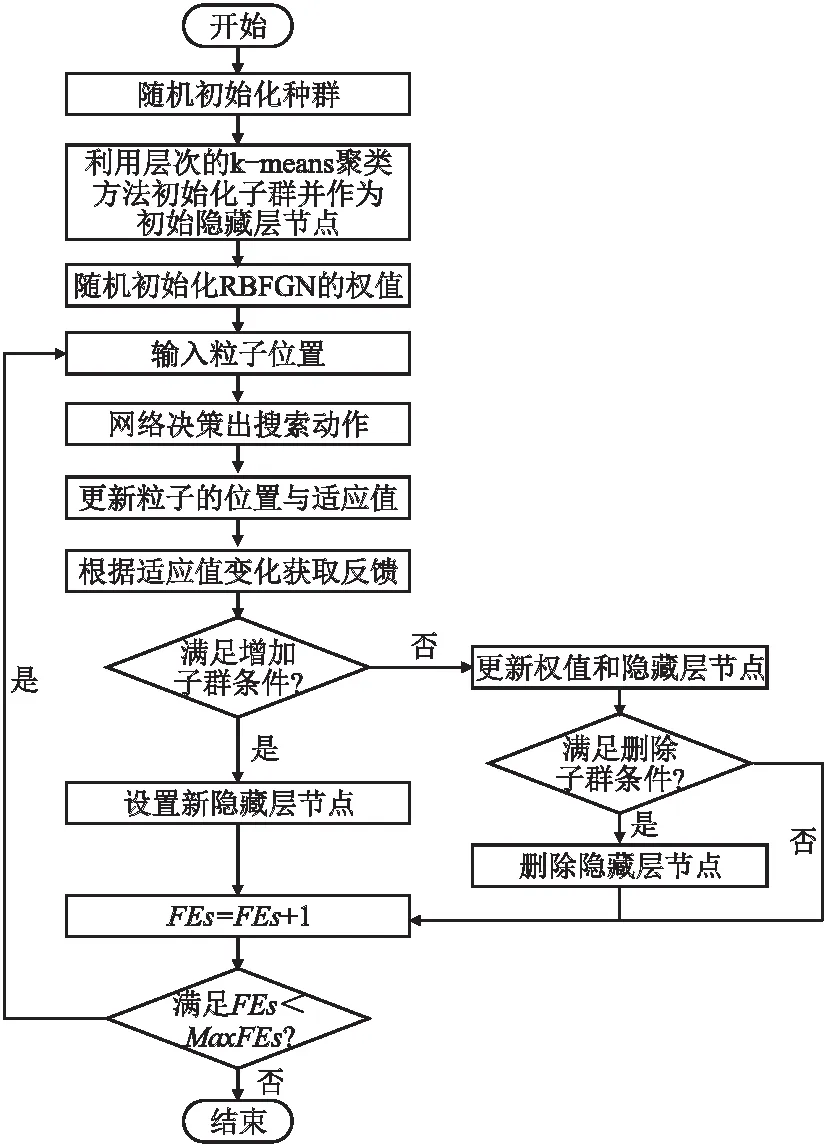
图2 RBFNN-PSO流程图Fig.2 Flowchart of RBFNN-PSO
算法1.
输入:MaxFEs:适应值函数最大的评估次数,N:种群规模,k:初始种群个数.
输出:gbest:最后一代中最优粒子的适应值.
步骤1.初始化种群;
步骤2.利用层次的k-means聚类方法初始化子群,作为RBFGN的初始隐藏层节点;
步骤3.随机初始化RBFGN的权值;
步骤4.输入粒子的位置到RBFGN;
步骤5.RBFGN决策出输入粒子的搜索动作;
步骤6.根据搜索动作更新输入粒子的位置与适应值;
步骤7.根据适应值变化获取反馈;
第三,农村区域出现不平衡的矛盾。现行“新农保”多缴多得的方式在市场经济中本无可厚非,但个人账户积累制易于出现“保富不保贫”以及扩大覆盖面难的问题。[7]同时,国家补贴具有不公平性,经济发达地区普遍好于欠发达地区,例如北京的养老金每人每月最高可达280元,而最低的地方每月基础养老金是55元。另外,在现有的财政体系下,经济欠发达地区资金普遍存在紧缺状况。因此,国家向农村提供的养老资源应充分考虑区域不平衡问题,做到养老资源供给的实质公平。
步骤8.根据公式(15)判断是否满足增加子群的条件,若满足,跳转至步骤9;否则,转至步骤10;
步骤9.设置新的隐藏层节点,包括节点中心、宽度及其与输出层相连的权值,并跳转至步骤13;
步骤10.更新权值和隐藏层节点;
步骤11.根据公式(23)判断是否满足删除子群的条件,若满足,跳转至步骤12;否则,转至步骤13;
步骤12.删除隐藏层节点;
步骤13.FEs=FEs+1;
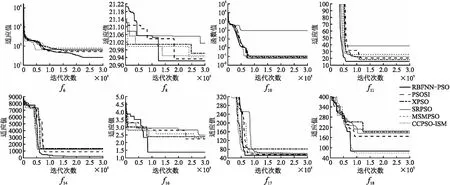
步骤14.判断算法是否满足FEs 由图2可以看出,RBFNN-PSO的时间复杂度主要源于初始化种群和RBFGN,通过网络前馈计算为输入粒子决策出相应的搜索动作,增加或删除RBFGN隐藏层节点(子群),以及更新RBFGN权值与隐藏层节点.对于D维搜索空间中的多峰优化问题,初始化规模为N的种群需要的时间复杂度为O(ND).基于初始的种群,本文利用层次的k-means聚类方法生成k个类簇中心,作为RBFGN的初始隐藏层节点(子群)中心,并初始化网络权值,其总的时间复杂度为O(kND)(k 假设当前隐藏层包括m个节点,在RBFGN的前馈计算过程中,实现对输入粒子两个搜索动作的决策.作为搜索动作之一,定位输入粒子的学习目标需要计算该粒子与m个子群中心的距离,以找出距其最近的子群中心,时间复杂度为O(mD+m)=O(mD).由于RBFGN前两层之间的连接只起到将输入粒子传递到隐藏层的作用(前两层间的权值均设置为1),在实际计算过程中,根据公式(4)输入的粒子直接参与每个隐藏层节点的响应值计算.根据响应的定义,需要计算输入粒子到每个隐藏层节点中心(共m个)的距离,而该距离在之前定位学习目标的过程中已获取,因此计算输入粒子在m个隐藏层节点上响应值的时间复杂度为O(m).作为RBFGN产生的另一搜索动作,调整输入粒子的加速系数其时间耗费主要发生在网络后两层间的前馈计算,以及输出层的动作选择(输出层共有3个节点,对应增加、减少加速系数,以及保持加速系数不变),决策出该动作所需的时间复杂度为O(m+3m+3)=O(m).因此,对于输入粒子,RBFGN决策出两个搜索动作的时间复杂度为O(mD+m)=O(mD). 利用RBFGN决策出的两个动作更新输入粒子的位置和适应值之后,基于公式(15)若增加子群的两个条件均满足,将选择当前的输入粒子作为新的隐藏层节点(子群)中心.在公式(15)中的条件中,为了判断种群中哪些粒子被分配到候选新子群,需要考虑种群中每个粒子(共N个)到m+1个隐藏层节点中心(包括候选新子群中心)的距离,而直接计算这些距离会造成昂贵的计算耗费.实际上只需计算每个粒子(共N个)到候选新子群中心的距离,其时间复杂度为O(ND).这是因为在完成初始子群划分之后,可利用一个N维的数组来保存每个粒子到其最近子群中心的距离(该距离首先由层次的k-means聚类方法得到,且该聚类方法只会执行一次).相应地,在后面每次更新各粒子到其最近子群中心的距离时,只需比较当前保存的距离和粒子到候选新子群中心间的距离,故计算公式(15)中条件的时间复杂度为O(ND).接着,利用公式(16)设置新子群中心的各项参数.对于输入的粒子,由于在之前的前馈计算过程中已经获得了计算该公式所需的μnr和ei,因此不会增加额外的时间复杂度.基于公式(15),若增加子群的任一条件不满足,则需更新RBFGN的隐藏层节点和权值.由3.4节的分析可知,对于输入的粒子,只需更新一个隐藏层节点,以及该节点与动作节点相连的一个权值.在更新过程中,公式(17)~公式(22)中的参数zac,yac和μnr已在之前的搜索动作决策过程中获得,也不会增加额外的时间复杂度.在更新过程之后,若公式(23)的任一条件满足,则会删除更新后不适合的隐藏层节点(子群).由于公式(23)与公式(15)中的条件均相反,类似地计算公式(23)所需的时间复杂度也为O(ND).值得注意的是,在每次迭代过程中增加隐藏层节点和删除隐藏层节点这两者最多只会执行其一,因此逐个输入种群中的粒子,算法总的时间复杂度为O(N2D). 本文选取CEC2013测试集[16]的15个多峰函数来反映RBFNN-PSO的表现.15个多峰函数如表 1所示. 15个多峰函数在每个维度上的搜索范围均设置为[-100,100].根据CEC2013的统一要求,MaxFEs设置为10000×D,其中D=30为搜索空间的维度.RBFNN-PSO的种群规模设置为50.为了公平比较,在15个测试函数上每种算法均独立运行30次,并计算其平均求解结果. 为了设置公式(15)和公式(23)中的,选择取值不同的在CEC2013测试集15个多峰函数上进行实验,其中的取值为0.001,0.01,0.1和1.表2给出不同取值下RBFNN-PSO在15个多峰函数上的平均适应值(Mean)及其标准差(Std.).每个函数上最好的平均适应值用黑体下划线标记,并在下方给出了Mean的平均排名,以展示不同取值下算法的综合表现. 表1 CEC2013多峰函数Table 1 Multimodal functions in CEC2013 由表2可以看出,当ε取值为0.01时RBFNN-PSO在除了f19之外的14个多峰函数上均取得了最好的平均适应值,并以1.07的平均排名在15个多峰函数上获得最好的综合表现.这是因为当ε=0.001时,重要性阈值过小,输入的粒子容易被初始化为新的子群中心,使得子群过多.由于种群规模有限(固定为50),过多的子群将造成有些子群中粒子个数较少,不利于子群的搜索.而当ε=0.1或ε=1时,重要性阈值过大,将造成子群数量不足,不利于保持种群多样性.因此在后续实验中我们将ε设置为0.01. 4.3.1 RBFNN-PSO与PSO变体算法比较 本文首先选择5种PSO变体算法进行比较,对比算法包括融入社会影响力的粒子群优化算法(PSO with Social Influence,PSOSI)[17],基于多榜样和遗忘能力的拓展粒子群优算法(An eXpanded Particle Swarm Optimization,XPSO)[18],自调整的粒子群优化算法(Self Regulating Particle Swarm Optimization Algorithm,SRPSO)[19],基于多种群的自适应迁移粒子的粒子群优化算法(Multi-Population Based Self-Adaptive Migration PSO,MSMPSO)[20],和带有信息共享机制的竞争和合作粒子群优化算法(Competitive and Cooperative Particle Swarm Optimization with Information Sharing Mechanism,CCPSO-ISM)[21].这些算法均采用其原始论文中的参数设置. 表3给出了6种算法在15个多峰测试函数上的平均适应值(Mean)及其标准差(Std.).每个函数上的最好平均适应值通过粗体下划线标记.为进一步展示各算法的综合表现,表4给出了6种算法在15个多峰测试函数上Mean的排名与平均排名.由表3可以看出,RBFNN-PSO在其中7个多峰测试函数(f6、f8、f10、f11、f14、f16和f17)上获得了最优的平均适应值.由表4可以看出,相比于其他5种算法RBFNN-PSO获得了最佳的综合表现,其平均排名为2.00,比取得次优表现的PSOSI,RBFNN-PSO在平均排名上低了0.80,其求解多峰优化问题的能力优势明显. 表3 6种算法在CEC2013测试集15个多峰函数上的平均求解结果比较Table 3 Comparisons of the mean resultsfor the 6 algorithms on the 15 multimodal functions of CEC2013 test suite 表4 6种算法在CEC2013测试集15个多峰函数上的分别排名与平均排名比较Table 4 Comparisons of the ranks and averageranks for the 6 algorithms on the 15 multimodal functions of CEC2013 test suite 为了更直观地展示算法的求解精度与收敛速度,图3给出在8个多峰测试函数(f6、f8、f10、f11、f14、f16、f17、f18)上,6种算法的适应值随迭代次数变化的曲线.从图3可以看出,除了f18,RBFNN-PSO在其他7个函数上均取得最好的求解精度,而且在其中的f11和f17上收敛最快.另外,根据RBFNN-PSO在f6、f8、f14、f16、f17上的收敛曲线,即使在其前期搜索精度不高的情况下,通过保持种群多样性与合理指导粒子搜索动作,RBFNN-PSO最终取得比其他5种算法更优的求解精度. 图3 6种算法的收敛曲线比较Fig.3 Comparisons of convergencecurves with respect to 6 algorithms 为了比较各个算法的寻优速度,在相同的仿真环境下,6种算法在CEC2013测试集的15个多峰函数上分别独立运行30次,表5记录了6种算法达到指定精度时的平均运行时间.由表5可以看出,在15个多峰函数上,RBFNN-PSO到达指定精度的时间消耗与其他5种对比算法大致相同,且相比于其他5种算法,RBFNN-PSO在f7、f11和f17上运行时间最短.基于3.7节的分析,RBFNN-PSO需要为每个输入粒子决策出相应的搜索动作,增加或删除RBFGN隐藏层节点(子群),以及更新权值与隐藏层节点,会造成一定的时间耗费,导致其时间复杂度的增加.但是由于其对搜索动作的出色决策能力,在达到指定精度时,运行的代数相对较少,从而在运行时间上和其他5种算法大致相同.然而,重要的是在表3和表4中本文提出的RBFNN-PSO在求解精度方面,相对于其他5种算法优势明显. 表5 6种算法在CEC2013测试集15个多峰函数上达到指定求解精度的运行时间比较(秒)Table 5 Comparisons of time for the 6 algorithms on the 15 multimodal functions of CEC2013 to achieve specified accuracy(s) 4.3.2 RBFNN-PSO与其他优化算法的比较 为了进一步验证本文所提出的RBFNN-PSO求解多峰优化问题的有效性,还将该算法与3种其他优化算法(非基于PSO的优化算法)进行比较,这些算法包括:CoDE[22]、PBILc[23]和AABC[24],分别属于差分进化算法、群体分布估计算法和人工蜂群算法的变体. 表6给出了RBFNN-PSO、CoDE、PBILc、AABC这4种算法在15个多峰测试函数上的平均适应值(Mean)及其标准差(Std.).每个函数上的最好平均适应值通过粗体下划线标记.为了展示各算法的综合表现,在表6的下方给出了其根据Mean的平均排名.从表6可以看出,相比于其他3种算法,RBFNN-PSO在7个函数(f6、f8、f12、f14、f17、f19和f20)上取得最好的平均适应值.而且根据平均排名,RBFNN-PSO获得最佳的综合表现,其平均排名为1.73.与取得次优综合表现的CoDE相比,RBFNN-PSO在平均排名上低了0.54,进一步验证了本文所提出的RBFNN-PSO求解多峰优化问题的有效性. 表6 4种算法在CEC2013测试集15个多峰函数上的平均求解结果比较Table 6 Comparisons of the mean resultsfor the 4 algorithms on the 15 multimodal functions of CEC2013 test suite 本文提出一种径向基函数神经网络指导的粒子群优化算法(RBFNN-PSO).该算法利用设计的径向基函数指导网络(RBFGN),在保持种群多样性的同时,合理定位粒子学习目标,有效调整粒子加速系数,以最终解决多峰优化问题.具体地,RBFGN将整个种群划分为多个子群,子群中心作为子群粒子的学习目标,指导其搜索.RBFGN充分考虑种群多样性,选择能代表子群搜索特性的粒子作为子群中心,并使之远离已存在的子群中心.因而,通过选择合适的子群中心,实现子群的划分.不同子群粒子在各自子群中心指导下搜索,呈现出多样的搜索特性,提升了种群多样性.RBFGN的输出层输出粒子加速系数的调整动作,并根据隐藏层决策出的学习目标,有效指导粒子的搜索.本文引入强化学习来训练网络,利用产生的反馈,期望获得最大的累积收益,实现对隐藏层节点,以及其与动作节点相连权值的有效调整. 为了反映RBFNN-PSO的表现,在CEC2013测试集上的15个多峰函数中开展广泛实验,通过与5种主流的PSO变体算法以及3种其他优化算法进行比较,其结果表明本文所提出的RBFNN-PSO求解多峰优化问题的能力优势明显.在下一步工作中,将把RBFNN-PSO应用于求解一些实际多峰优化问题,并将其拓展到更复杂的优化领域,例如动态优化领域和大规模优化领域等.3.7 算法时间复杂度分析
4 仿真实验及结果分析
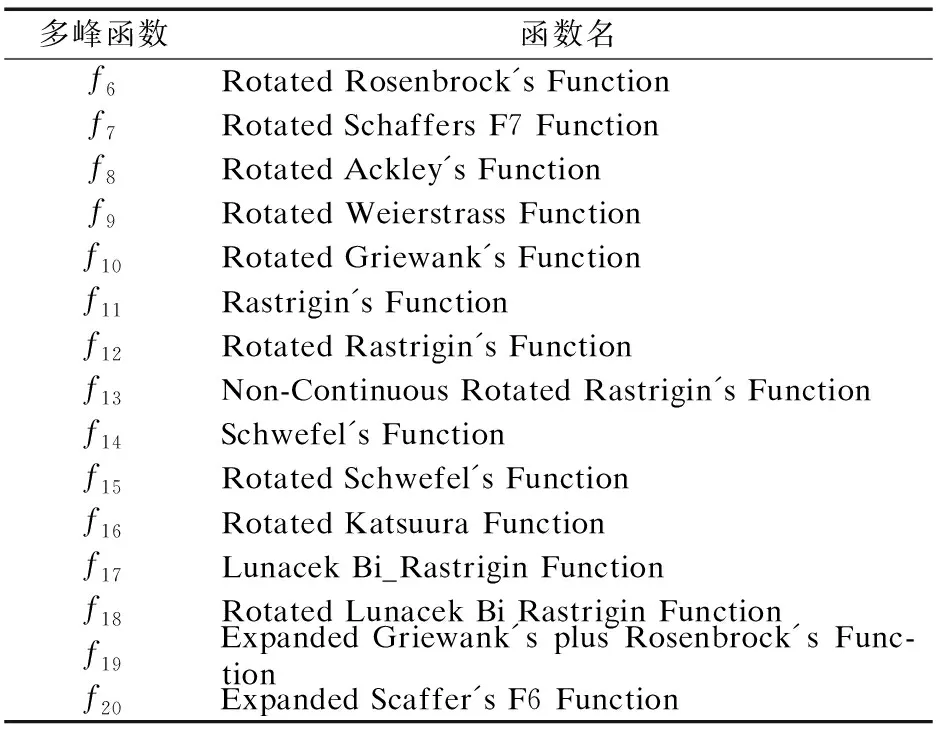
4.1 测试函数
4.2 参数设置
4.3 实验结果与分析




5 结 论
