计及MCMC 方法的电网概率检修计划指标优化模型*

2023-11-10郭子强宋涛郭杰王健张天毅

电子技术应用 2023年10期

郭子强，宋涛，郭杰，王健，张天毅

（国网甘肃省电力公司兰州供电公司，甘肃兰州 730070）

0 引言

随着电力系统的有力发展，电力系统设备可靠性大幅提高，经济性和可靠性并行成为目前电网发展的主要方向[1]。正确应对电网可能出现的设备损毁问题，合理安排检修内容、制定检修计划成为保障电力系统稳定发展的重要内容[2-3]。

在信息技术以及物联网技术的发展过程中，电力智能化逐渐成为电力行业发展的重点方向，目前的电力检修研究内容也集中于检修辅助系统的开发[4]、电力设备状态评价体系[5]以及故障检测定位技术研究[6]。作为电力产业价值链中的重要一环，适当的电力检修计划安排可以提升电网的供电可靠性以及电力用户的满意度，电力公司通过对设备的检修延长设备的运行年限，降低电网因设备故障导致停运的可能性，从而降低电力公司的经济损失，提升电力检修环节在电力产业链条中的价值创造。从另一方面来说，电网停止供电所导致的不仅是供电方的经济损失，也会致使电力用户的电力中断，从而带来额外的社会经济损失[7]。

文献[8]提出了一种利用设备历史数据对设备故障可能性进行预测的检修优化策略，但是该检修优化策略在需要大量数据支撑的同时，也考验着设备的在线数据监测能力，这无疑极大地提高了检修的成本。文献[9]阐述了变电站一次设备的运维技术，但是没有进一步对检修的内容进行详细说明。文献[7]针对智能电站结构建立一套状态检修策略，构建了设备维修评价决策管理体系，但是并无对电网检修经济性的探讨。文献[11]提出一类电力运维结构的故障自动检修优化策略，但是文中仅对检修检测的结果进行分析，并无对检修计划可靠性与经济性的讨论。以上文献均无对检修模型的构建及其可用性进行详细研究。

本文基于上述内容，提出一种新的概率检修方案，首先根据实际设备情况构建电力设备检修模型；根据所提决策变量对设备检修模型进行补充优化；基于马尔可夫链-蒙特卡洛(Markov Chain Monte Carlo,MCMC)法构建概率检修模型；通过仿真构建数学模型对两种不同检修优化策略的可靠性和经济性进行分析；最后采用粒子群算法对不同检修优化模型的最优解进行比较。

1 检修模型与决策变量

本节首先构建检修计划模型，然后提出基于决策变量的检修模型，以便进一步考察检修计划的可靠性和经济性。

1.1 检修模型

本文所构建的检修计划模型是基于被检修设备的状态，因此首先需要对设备的状态进行分级，其次再根据检修的细致程度对检修程度进行分级[12]，并对处于不同状态等级的设备设置相应的劣化速率。图1 所示为设备状态分级情况。

图1 设备状态分级情况

从图1 可以看出，根据设备目前的状态将设备分为四个状态等级：正常状态、警告状态、高危状态以及故障状态。其中将警告状态再细分为两个等级，分别为Ⅰ级警告状态与Ⅱ级警告状态；将高危状态再细分为三个等级，分别为Ⅰ级高危状态、Ⅱ级高危状态和Ⅲ级高危状态。根据检修的细致程度将检修程度分为三个等级：日常检修、次要检修和重要检修，三类检修的耗时分别约为一小时、一天、一周，检修耗费包含人工费和材料费。

设备状态的变化并不总是在连续阶段之间变换，在某种特定情况下会出现跨阶段变化。

表1 为设备各状态阶段的日常检修概率和年劣化速率，其中α1＜α2＜α3，β1＜β2＜β3。检修概率若为1，则年检修次数为1；劣化率指当年的设备状况与上一年设备状况劣化情况的变化率。需要注意的是，检修对设备的影响存在三种情况：改善、维持、受损；如果设备运行全过程中从未参与过检修，那么设备经历正常、警告Ⅰ级、高危Ⅰ级后直接进入故障状态，不存在其他设备状态阶段。

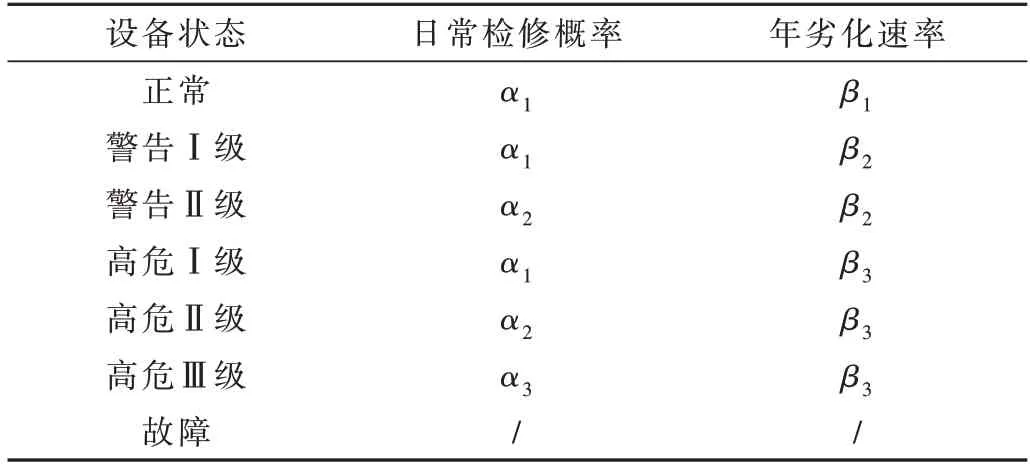
表1 设备各阶段劣化趋势

设备在检修过程中可能发生以下几类情况：

(1)处于警告Ⅰ级状态的设备在经过日常检修后，必定需要进行次要检修，次要检修后约有50%的设备将被改善并恢复正常状态，44%的设备归入警告Ⅱ级状态，1%的设备归入高危Ⅲ级状态；

(2)处于警告Ⅰ级状态的设备在经过次要检修后，约有5%的设备需要进行重要检修，重要检修后约有90%的设备被改善并恢复到正常状态，10%的设备被归入警告Ⅱ级状态；

(3)处于高危Ⅰ级状态的设备在经过日常检修后，约有10%的设备仅需进行次要检修，90%的设备需要进行重要检修；

(4)处于高危Ⅰ级状态的设备并经过次要检修后约有80%的设备需进行重要检修，10%的设备归入警告Ⅱ级状态，10%的设备被归入高危Ⅲ级状态；

(5)处于高危Ⅰ级状态的设备并经过重要检修后，约有90%的设备被改善并恢复到正常状态，10%的设备被改善并被归入警告Ⅱ级状态。

上述检修判别情况可以归纳如图2 所示。

图2 检修判别情况归纳

1.2 基于决策变量的检修模型

本文将电力设备的日常检修概率p作为检修计划的决策变量，进一步完善检修计划模型。为了量化检修计划的可靠性和经济性指标，需要进一步完善检修模型。

(1)设备停运模型

本文采用马尔可夫链-蒙特卡洛法计算电网设备从投入使用到故障状态所经历的时间。设备的状态采用马尔可夫两状态模拟，此时假定设备仅存在正常运行和故障两种状态，此时的设备停运模型f i(t)为[13]：

式中，i为设备编号，β为设备劣化速率。

(2)检修成本

年检修成本包含日常检修、次要检修和重要检修三类的检修的成本，三类年检修次数的计算公式为：

式中，c(MHi)、c(MDi)、c(MWi)分别为处于正常、警告、高危状态设备的年检修次数，d表示平均年检修时间，p表示检修概率。

年检修成本计算公式为：

式中，CMH、CMD、CMW分别为一次日常检修、次要检修、重要检修的耗费。

(3)设备停用率

由于设备处于检修状态或故障状态导致设备处于停用状态，此时电网设备停用率U表示为：

式中，p(MHi)、p(MDi)、p(MWi)为处于日常检修、次要检修、重要检修的概率，p(F)为设备故障的概率。

(4)停电经济损失

由于设备检修停用导致用户电力供给中断，将会造成的额外经济损失，经济损失评估涉及电力系统的结构、用户性质、负荷重要程度、设备位置、停电时间、可调节负荷量、失电量等因素，其中用户性质、负荷量和停电时间为主要因素，此时停电经济损失CU 的计算表达式为：

式中，CP为每小时每千瓦的经济损失，γ为用户性质因数，L为损失负荷总量。用户性质因数表如表2 所示。

表2 用户性质因数

2 基于马蒙法的概率检修模型

马尔可夫链-蒙特卡洛法被广泛应用于统计调整领域，马-蒙法的特点是，系统下一时刻的状态取决于当前状态和系统的变化过程，可以用于表征复杂程度极高的电力系统，本文将马-蒙法应用于检修模型[13]。

根据马尔可夫链-蒙特卡洛法，基于概率的状态变化满足以下表达式：

令t=0，可得微分方程：

引入矩阵q=p'(0)，该矩阵表示为：

式中，n、m为大于零的正整数。

同时，矩阵q需满足以下条件：

将电力系统中的任一设备看作一个元素，该元素出现异常状态看作事件A，检修该元素看作事件B，其中事件A 和B 在Δt时间内发生的概率分别为λ和μ，事件A和B 不存在同时发生的可能性。此时系统仅存在两种状态：0 和1。其中，0 代表设备处于运行状态，1 代表设备处于故障状态。此时Δt时间内事件发生的概率被表示为：

概率矩阵q被定义为：

此时，基于概率矩阵q可以作出如图3 所示的状态变化过程图。

图3 状态变化过程图

根据图3 和马-蒙法可以列出状态概率的微分方程：

其中，0 状态方程的通解和特殊解为：

式中，A为常数，其值取决于系统的初始状态。

由式(12)和式(13)可得状态概率方程为：

由于系统的初始状态为正常运行状态，即0 状态，由此可将公式(14)变换为：

根据式(15)，将电力系统设备数量推广到N个电力设备，此时的状态概率方程变换为：

此时推广到N个电力设备的检修状态变化过程图如图4 所示。

为校验加入马-蒙法后的电网检修模型的准确程度，本文随机选取兰州地区40 个网络节点进行测试，其中包含电缆、变压器、绝缘子、断路器四类设备。采用日常巡视记录数据与算法计算数据结果进行准确程度的对比，结果如图5 所示。

图5 准确程度对比

图5 所示对比图分别为加入马-蒙法前后的数据准确度情况。图5 所示三个坐标轴分别表示节点编号、时间和准确程度。其中节点编号代表设备编号，四类设备分别选取10 个节点，共计40 个节点，设备编号表如表3所示；设备数据的时间点选取规则为一天选取1 个点，包含初始数据在内共计选取25 个数据点。

表3 设备类型表

从图5 可以看出，在加入马-蒙法前的电网模型数据表征情况较为混乱，加入马-蒙法后的电网数据模型准确程度有较好的改善。如图5(b)所示，不同类型设备的设备状态表征存在差异，其中变压器的设备状态表征随时间变化，其准确程度变化最为明显。

3 算例分析

本节以甘肃省实际电网线路设备情况为依托，根据本文所搭建的设备检修模型进行算例分析。为了进一步验证检修计划优化策略，通过修改检修概率α1、α2、α3的取值，分析电力设备从投入运行到进入故障状态的年限和总成本变化，进一步得出可实现检修计划可靠性和经济性指标优化的目标函数。

传统检修计划的检修概率情况如表4 所示。从表4可以看出，传统检修计划下的日常检修概率仅存在三种不同的情况，处于正常、警告、高危的设备检修概率分别为α1、α2、α3，其检修结果判别与图2 所示概率检修结果判别一致。

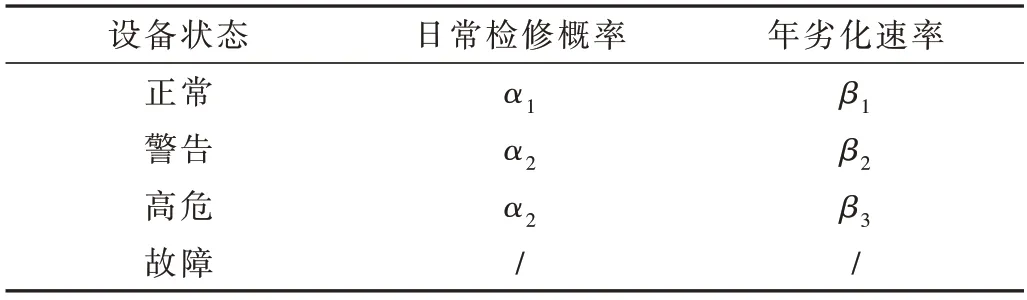
表4 传统检修计划检修概率表

3.1 可靠性和经济性指标优化条件

图6～图8 分别展示了在两种不同检修策略的作用下，设备运行年限的变化情况，分别为仅改变α1、仅改变α2、仅改变α3检修概率的情况下，线路设备的运行年限的变化情况。

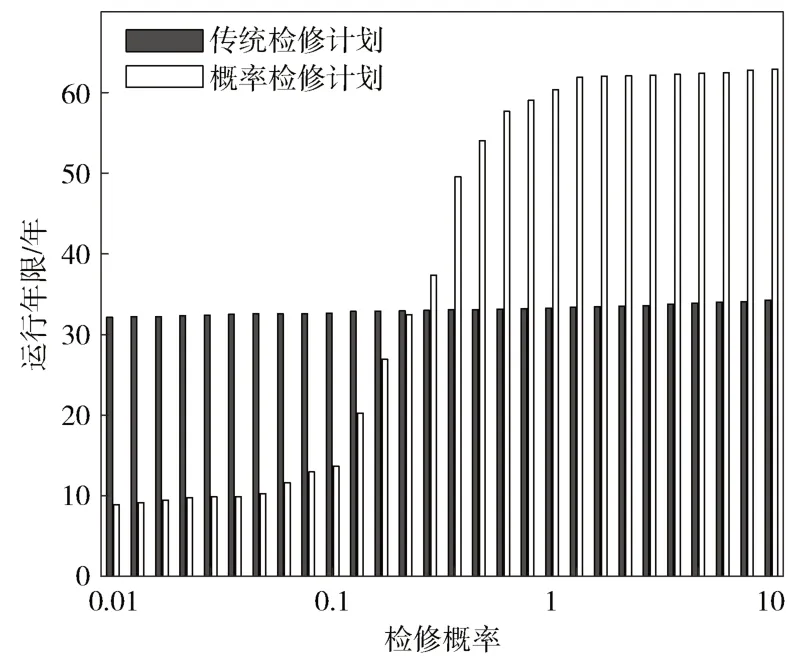
图6 仅改变α1 运行年限变化情况

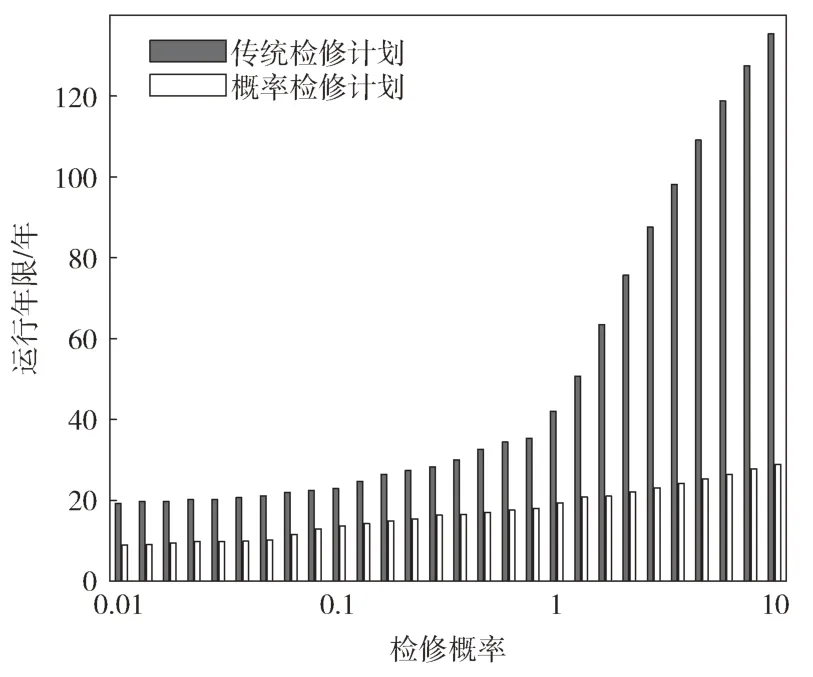
图7 仅改变α2 运行年限变化情况

图8 仅改变α3 运行年限变化情况

图9 仅改变α1 运行总成本变化情况

根据传统检修计划的仿真结果，设备可以通过提高α1实现设备运行年限的增加，当α1保持在比较小的数值时，此时α2、α3对设备运行年限的影响较小；根据概率检修计划的仿真结果，α1对设备年限的影响较小，此时为了增加设备年限，可以通过增加α2、α3实现。由于检修概率α1、α2、α3不能被无限提高，因此无法通过最大化目标函数的方式实现最优检修概率的选取，为了实现检修概率的最优选取，需要选取检修概率的约束条件，本文将线路设备的运行年限最小值限制在电网规划所需的最小运行年限。

图8～图11 分别展示了在两种不同检修策略的作用下，设备运行总成本的变化情况，分别为仅改变α1、仅改变α2、仅改变α3检修概率的情况下，线路设备运行总成本的变化情况。

图11 仅改变α3 运行总成本变化情况

根据两种不同检修策略作用的仿真结果，可以通过选取最优的检修概率，实现设备运行总成本的降低。根据传统检修计划的仿真结果，在检修概率于0.01～10 的变化过程中，总存在一个运行总成本最小值；根据概率检修计划的仿真结果，为了降低运行总成本，可以通过降低检修概率α1，提高检修概率α2、α3实现。

根据以上仿真结果，将设备运行年限纳入检修计划目标函数约束条件，将设备运行总成本纳入检修计划目标函数优化。目标函数OF 表示为：

3.2 粒子群算法优化结果选取

根据3.1 的仿真结果，由于运行总成本与检修概率α1、α2、α3之间呈现高度非线性，在此情况下若仅将设备运行成本最小作为优化条件，无法人为精确寻找检修概率α1、α2、α3的最优值。需要注意的是，本文的研究点集中于不同检修优化策略对可靠性和经济性的影响，因此采用何种算法并不影响检修优化策略的可靠性和经济性程度。在上述情况下，本文采用粒子群算法进行最优检修概率选取[15]。粒子群算法流程如下：

(1)初始化粒子群

对检修概率α1、α2、α3分别定义一个初始种群规模N，每个粒子的位置Xk和速度Vk，此处需对检修概率的最大值和最小值进行约束。

(2)适应度值Fitness 计算

利用目标函数OF 对每个粒子的适应度Fitness 进行计算，此处的目标函数分别以检修概率α1、α2、α3为变量，分别定义为OF(α1)、OF (α2)、OF (α3)。

(3)粒子个体极值pBest 计算

根据目标函数OF (α1)、OF (α2)、OF (α3)分别计算每个粒子的个体极值pBest。

(4)全局极值gBest(αi)计算

分别计算OF (α1)、OF (α2)、OF (α3)的全局极值gBest(α1)、gBest(α2)、gBest(α3)。

(5)全局均值gBest 和距离dgBest 计算

根据OF (α1)、OF (α2)、OF (α3)的全局极值计算其全局矢量均值和距离，全局矢量均值计算公式为：

(6)粒子间距dpBest 计算

粒子间距dpBest 表示粒子个体极值pBest 之间的距离。

(7)个体极值pBest 选取

用于更新每个粒子位置Xk和速度Vk。

(8)根据步骤(5)和步骤(7)更新每个粒子位置Xk和速度Vk，并根据粒子位置计算设备运行年限、运行总成本和设备停用率。

(9)若满足目标条件，退出算法，若不满足目标条件，返回步骤(2)。

算法采用的参数如表5 所示，表中c为学习因子。ω为惯性权重。

表5 算法参数

表6 和表7 为粒子群算法计算结果，其展示了随着检修概率的变化，设备运行年限、设备停用率和运行总成本的数据情况。

表7 概率检修计划数据

根据表6 传统检修计划的计算结果数据显示，采用传统检修计划的检修概率α1、α2、α3最优值分别为5、8.2、10，其表明了随着电力设备劣化过程的进行，其检修概率的提高有益于电力设备运行年限的提升和设备停用率、运行总成本的降低；根据表7 概率检修计划的计算结果数据显示，采用概率检修计划的检修概率最优值分别为1、10、10，其表明了概率检修计划的最优检修安排为在设备劣化进程的前期不安排检修计划，即检修概率α1始终为1，在劣化进程的中后期安排检修计划，并且随着检修概率的升高，电力设备的运行年限随之升高，设备停用率和运行总成本逐渐降低。

从表6 传统检修计划与表7 概率检修计划的数据可以看出：当检修概率α1、α2、α3均为1时，两种检修计划下的电力设备运行总成本存在0.2 万元的差距，概率检修计划下的设备运行年限相较于传统检修计划下少2年；随着检修概率α2、α3的提升，概率检修计划下的设备运行总成本快速降低，并始终少于传统检修计划下的运行总成本；随着检修概率α2、α3的提升，概率检修计划下的设备停用率始终小于传统检修计划下的设备停用率；在两种检修计划下的检修概率α2、α3均小于6时，传统检修计划下的设备运行年限始终大于概率检修计划下的运行年限，当检修概率α2、α3超过6时，概率检修计划下的设备运行年限将远大于传统检修计划下的设备运行年限。相较于最优检修概率下的传统检修计划，概率检修计划的运行年限增长了约1.6倍，设备停用率降低了23.3%，运行总成本降低了12.1%。综上所述，概率检修计划为电力产业创造的价值体现在运行总成本和设备停用率的降低，并随着设备劣化进程中后期的检修次数的增加，设备运行年限也将快速增长，提升了电力产业价值链中电力检修环节的价值增值，因此概率检修计划的可靠性和经济性效益优于传统检修计划。