结合不确定性估计的轻量级人体关键点检测算法

王亚东，秦会斌

（杭州电子科技大学 新型电子器件与应用研究所，浙江 杭州 310018）

0 引言

随着社会发展，监控视频分析正从人工走向智能，从传统走向现代。人体关键点检测是以人为中心的视频分析中的重要环节，又称为人体姿态估计[1]。人体关键点是具有明确语义的关节点和部位，是行为识别[2]、人机交互[3]和动作捕捉[4]等应用的重要基础。

随着卷积神经网络（Convolutional Neural Network，CNN）的发展，人体关键点检测取得显著进步，精度逐渐提升。基于深度卷积神经网络的人体关键点检测算法分为两类：基于热图表示的检测方法和基于坐标表示的回归方法。

自从Tompson 等人[5]首次提出用热图表示关节点，检测方法成为二维姿态估计的主流。孙科等人[6]针对关键点检测任务提出HRNet，整个网络中保持高分辨率的特征图，通过并行连接多个不同分辨率的子网络，并在它们之间进行信息交互和融合，避免了信息的丢失和模糊。检测方法具有精度高、训练效率高和空间泛化性好等优点。但是热图分辨率低于原图分辨率导致的量化误差和解码过程中argmax 操作不可微分，使得检测方法依赖高分辨率热图，限制了在嵌入式设备中的使用。

回归方法在人体姿态估计中研究较早，但相关工作较少。回归方法直接端到端产生图像中关键点的坐标。Toshev 等人[7]首次提出利用CNN 回归坐标进行人体姿态估计。Carreira 等人[8]提出了一个迭代误差反馈框架（Iterative Error Feedback，IEF），引入自上而下的反馈，预测当前估算值的偏移量并进行迭代矫正。Nie 等人[9]提出了单阶段的多人姿态估计网络（Single-stage Multiperson Pose Machine，SPM），采用根节点预测人体位置，然后预测关节点的偏移量。回归方法拥有简单灵活高效等优点，但性能仍逊色于检测方法，尤其在遮挡、截断和运动模糊等场景中误差较大。

实际应用中，往往需要在计算能力弱和内存空间有限的设备上运行神经网络，大型神经网络难以在移动端和嵌入式设备部署，为此研究人员提出一系列轻量级模型，例如MobileNets[10]、ShuffleNet[11]和MicroNet[12]。轻量级模型基于空洞卷积、可分离卷积和组卷积等操作，减少网络参数和计算量，而不损失网络性能。但这些网络大多是为了目标检测而设计，对于人体关键点检测缺少针对性。

为了解决人体姿态估计在移动端的性能问题，本文改进积分姿态回归[13]算法（Integral Pose Regression，IPR），以轻量的Lite-HRNet[14]为主干网络，使用低分辨率的热图编码和soft-argmax 解码来降低时空复杂度。针对标注的模糊性，结合不确定性估计进行误差分布估计，预测分布的尺度参数；根据最大似然估计，提出尺度损失。更进一步，利用预测的尺度参数，人工渲染目标热图进行监督，对隐式热图中概率分布进行约束。COCO[15]数据集上实验结果表明，与积分姿态回归算法相比，热图分辨率为64×48 的改进算法提高了1.7%的平均精度，热图分辨率为16×12 的改进算法提高了3.3%的平均精度，降低了资源占用。

1 IPR 算法原理

IPR 算法结合了检测方法和回归方法的优点，编码过程中使用低分辨率隐式热图代替高分辨率热图，解码过程中使用可微分的soft-argmax 代替argmax。

检测方法把CNN 作为滤波器，针对每类关键点产生二维网格状热图，每个像素值表示此处包含关键点的概率，称为编码过程，如图1 (a)所示。通过argmax 获得热图中概率最大的位置坐标映射到原图坐标，称为解码过程。检测方法按标注信息人工渲染每个关键点的高斯热图作为目标，对输出热图进行密集监督。

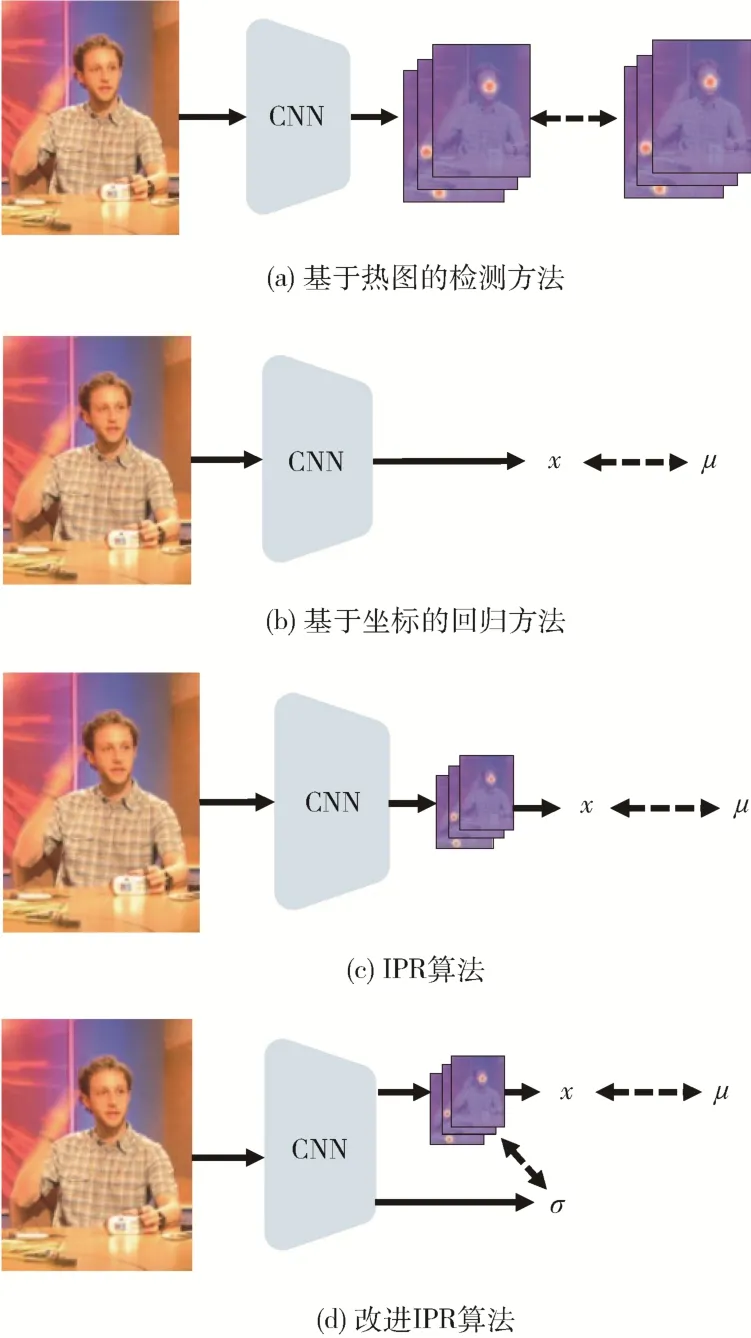
图1 人体关键点检测方法示意图

检测方法依赖高分辨率的输出热图，因为高分辨率热图可以提供更精细的关键点定位，保留更多的图像细节和语义信息，有利于提高关键点检测的准确性和鲁棒性。但高分辨率热图需要更多的计算资源、内存空间和训练时间，存在量化误差和分辨率限制，不能完全避免关键点定位的偏差和不确定性。因此轻量级的关键点检测必须克服对高分辨率热图的依赖，在低分辨率时保持较高的精度。

回归方法的基本思想是将关键点检测问题转化为坐标回归问题，直接同时预测每个关键点在图像中的坐标，过程中无热图，如图1 (b)所示。编码过程和解码过程完全由神经网络完成，外部难以解释和控制。优点是可以简化姿态估计的流程，缺点是性能不如检测方法。

IPR 算法的编码过程与检测方法大同小异，区别在于IPR 算法产生的热图分辨率较低，如图1(c)所示。对于输入图像I中每个关键点，模型输出一张热图∈RM×N，其中M和N是热图的高和宽。热图中每个像素的值表示此处包含关键点的概率P(J|I)，其中J∈R1×2是在图像I上的坐标。选取人体的K个关键点，模型同时预测K张热图，对应不同的关键点，记为∈RK×M×N。例如K为17，对于分辨率为256 × 192 的图像，模型输出17 张热图，分辨率为原图的1/4，即的形状为17 × 64 × 48。

IPR 算法的解码过程与检测方法大相径庭。对于每个关键点，使用soft-argmax 从热图得到关键点坐标。具体过程为：对于模型输出的热图，通过softmax 操作使热图的和为1，得到归一化热图，如式(1)所示。在x轴和y轴上按坐标对取期望，如式(2)所示，得到关键点在各轴上的坐标和。所得坐标近似热图最大值所在坐标，此过程可微分且没有量化误差。

其中，Ω为热图中所有像素点坐标的集合，p和p'是热图上的坐标，为热图上p位置对应值。β为人工选取的控制softmax 平滑程度的参数,β越小越平滑，当热图分辨率为64×48时β取14，为16×12时β取10。

soft-argmax 解码过程如下：

输入:h热图，形状为[H,W];beta 指数因子。

输出: [x,y] 最大值的坐标。

2 改进的IPR 算法

2.1 不确定性估计

IPR 算法仅预测关键点坐标，对预测坐标的可信程度无法预测，对预测坐标与真实坐标的误差难以有效评估。

给定输入图像I，关键点标注坐标为μ，模型的预测坐标为x，两者距离称为误差。不同的误差分布对应不同的损失函数。

以一维坐标系为例，关键点坐标的标注值为μ时，分布应为如图2 所示的狄拉克分布。训练网络时使用的均方误差损失函数意味着网络输出的是高斯分布的期望值，忽略了高斯分布的方差。图2 中两个高斯分布期望相同，但高且集中的高斯分布方差更小，更接近理想分布，可信程度更高。

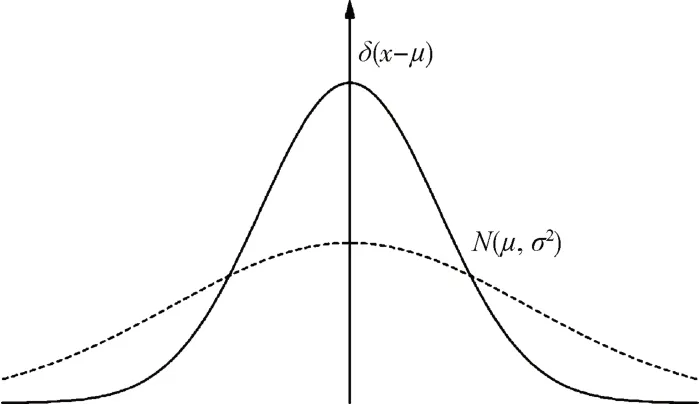
图2 目标分布与预测分布示意图

此外，准确的标注信息利于训练模型，但由于关键点和部位是一个区域而非一个点，人工误差无法避免，标注不可能完全准确，具有模糊性。

为了降低标注误差对训练的影响，提高结果的可信程度，提出结合不确定性估计，让网络为每个关键点预测一个尺度参数，预测结果误差分布的尺度参数。在基于热图的检测方法中，人工渲染的高斯热图中关键点周围的像素值非零，可视为对标注模糊性的补偿和软化标签，与不确定性估计异曲同工。

由于标注值与真实值的误差更接近拉普拉斯分布，这里假设误差分布服从拉普拉斯分布，即：

式中，x为预测坐标，μ为标注坐标，为预测尺度参数，θ表示模型的可学习参数。

最大似然估计是一种基于概率分布的参数估计方法，它的目标是找到一组参数，使得给定数据的概率最大。根据式(3)，得到似然函数：

按照最大似然估计，使得标注坐标处的似然程度最大，使用对数似然作为损失函数。若固定为1，忽略常数得到常用的损失函数L1距离。

本文使用的主干网络为Lite-HRNet，在Small HRNet和HRNet[6]的基础上添加跨分辨率的通道注意力机制，进一步提高了精度，网络结构图如图3 所示。

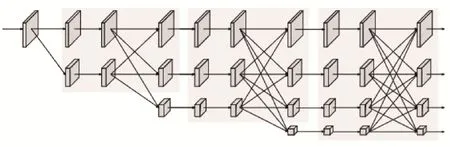
图3 主干网络结构图

结合不确定性估计的网络头部如图4 所示，把主干网络的输出特征图作为头部网络的输入特征图，将输入特征图拆分，一部分作为热图，一部分用于不确定性估计。进行不确定性估计时，对特征图做全局平均池化（Global Average Pooling，GAP），再经过全连接层产生K个σ，即每个关键点误差分布的尺度参数。

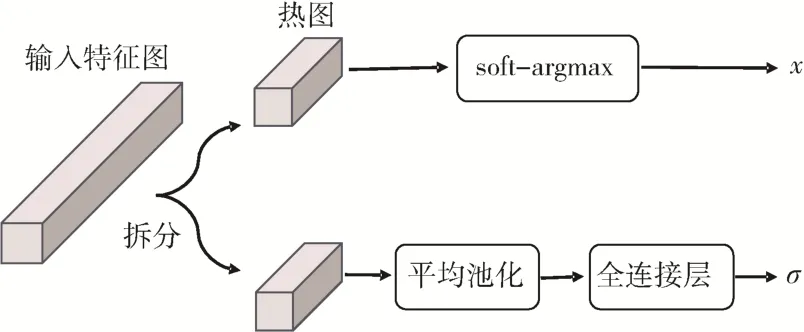
图4 头部网络结构图

根据式(4)设计尺度损失Lre，用来评估模型输出和真实标签之间的差异，如式(5)所示。

2.2 监督隐式热图

IPR 算法和改进后的IPR 算法都是比较预测坐标和标注坐标，训练时效率较低，难以优化和控制。本文利用不确定性估计得到的尺度参数对隐式热图进行直接监督。

对比IPR 和DSNT[16]，发现在高分辨率情况下，IPR精度低于检测方法，随着分辨率的降低，IPR 仍能保持较高的精度，而检测方法迅速下降。Gu 等人[17]通过将样本按不同难度划分，实验发现IPR 在难样本中的效果较好，检测方法在简单样本中的效果较好，其他情况两者相当，原因是隐式热图的概率分布形状不规则和解码方式导致的梯度消失。

对热图取期望是从热图到坐标的映射，多种热图对应一个坐标，只有集中且规则的热图才具有良好的泛化性和稳健性，如图5 所示，从左到右热图逐渐收敛，最右边热图的稳定性最好。

图5 不同形状的热图

本文利用不确定性估计得到的尺度参数σ̂对隐式热图进行直接监督。对于一个关键点，根据标注坐标μ和尺度参数渲染高斯热图，逐像素计算与输出热图的距离。热图损失函数为Lde，如式(6)所示：

最终模型的损失函数为两者的组合，如式(7)所示，热图损失的权重为λ。训练开始时λ较大可以加速训练，训练后期调小λ或取零进行微调。总损失为K张热图的损失之和。

3 实验与结果

本文实验在Ubuntu 18.04 操作系统下运行，CPU 为Intel Xeon Gold 6148 @ 2.40 GHz，GPU 为Tesla V100，显存为16 GB，CUDA 版本为11.2，采用飞浆深度学习框架，版本号为2.4.0。

对本文算法的实验将在COCO 数据集[15]上按照自顶向下框架进行。第一步为人体检测：检测图像中的人，得到单人边界框；剪裁得到多张单人图像，分别进行人体姿态估计。第二步为姿态估计：给定单人图像I作为输入，得到K个关键点在I中的坐标作为输出。

COCO 数据集有超过20 万张图像和25 万个标注17个关键点的人体实例。本文的模型在train2017 数据集上训练，在val2017 数据集上验证和测试。

部分实验结果如图6 所示，模型对于单人和多人场景、近景和远景都能检测，对遮挡鲁棒。

图6 部分检测结果

3.1 实验设置

模型的主干网络均为Lite-HRNet-30，选取Adam 优化器，批次大小为128，初始学习率为0.002，在第170 轮和200 轮学习率缩小10 倍。

训练时，人体边界框高宽比为4:3，从原图中剪裁出实例图，然后双线性插值产生分辨率为256 × 192 的图像。每个实例图都会经过数据增强，包括随机旋转([-30°,30°])、随机放 缩([0.75,1.25])、随机水平翻转和 上半身数据增强。

前向推理时，采用自顶向下框架，使用人体检测网络得到人体边界框，再剪裁出实例图预测人体关键点。人体检测网络使用Faster R-CNN[18]。预测时，将进行翻转测试，翻转图像和未翻转的热图相加，然后计算坐标，除此之外，无其他后处理过程。

评估时，本文采用目标关键点相似性（Object Keypoint Similarity，OKS）测量预测姿态和真实姿态的距离，报告标准的平均精度和召回率。

3.2 对比试验

本文算法对比Lite-HRNet 和IPR 在COCO 验证集上的结果如表1 所示（L-HR 代表Lite-HRNet）。3 种模型均以分辨率为256×192 的图像为输入，产生热图有分辨率为64×48 和16×12 两种，前者像 素数量是后 者的16 倍。评价指标使用平均精度AP，而AP50和AP75分别是OKS阈值为50%和75%时计算出的平均精度，APM和APL分别是中等面积和大面积时的平均精度，AR 则是平均召回率。

结果显示，3 种模型热图分辨率缩小时精度分别下降了13.2%、2.6%和1%，证明本文算法对热图分辨率的变化最不敏感。在高分辨率热图下，本文算法和Lite-HRNet 表现相当，相比IPR 提升1.7%，而在低分辨率热图下，本文算法远超Lite-HRNet 和IPR，分别超过12.1%和3.3%。低分辨率的本文算法相比高分辨率的IPR 算法，平均精度提高了0.7%，证明了本文算法克服了对高分辨率热图的依赖，在低分辨率时保持较高的精度。

3.3 消融实验

为验证本文算法中尺度损失和热图约束的有效性，对两个关键模块做消融实验。在COCO 测试集中，分别固定网络的热图分辨率为64×48 和16×12，实验3 种模型中，模型A 为IPR 算法，模型B 为IPR 算法加不确定性估计，模型C 为模型B 加隐式热图监督，结果如表2 和表3所示。

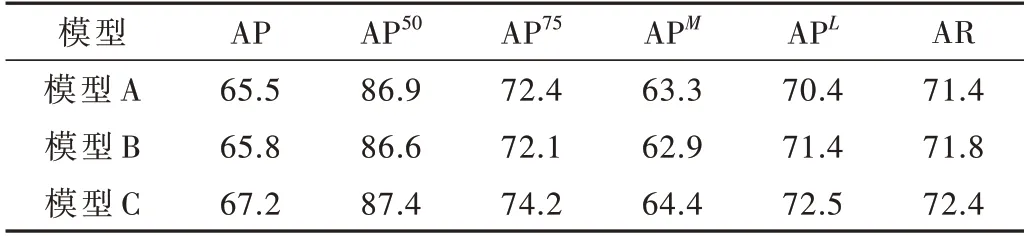
表2 热图分辨率为64×48 的消融实验（%）

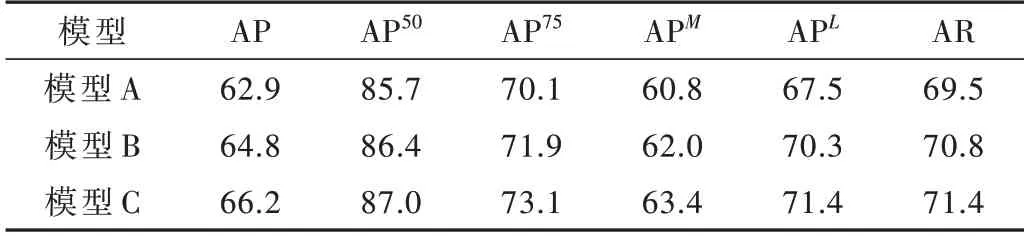
表3 热图分辨率为16×12 的消融实验（%）

表2 中高分辨率时在IPR 的基础上增加不确定性估计，平均精度提高0.3%，更进一步约束热图，平均精度再提高1.4%。

表3 中低分辨率时在IPR 的基础上增加不确定性估计，平均精度提高1.9%，更进一步约束热图，平均精度再提高1.4%。

消融实验的结果验证了不确定性估计和隐式热图监督的有效性，提高了IPR 算法的精度和效率。

4 结论

本文以IPR 为基础，提出一种结合不确定性估计的轻量级人体关键点检测算法，采用轻量级的主干网络Lite-HRNet，设计了轻量级的头部网络，添加了对误差分布方差的预测，设计了新的尺度损失函数，使预测结果的精度和可信度提高。利用预测的方差，渲染热图对隐式热图进行监督，约束热图的形状，提高了网络的精度和鲁棒性，获得更好的估计结果。本文在COCO 数据集上进行了消融实验和对比试验。消融实验验证了不确定性估计和监督隐式热图的有效性。对比试验中当隐式热图的分辨率是高分辨率网络的1/16时，本文算法仍能保证平均精度只下降了1.1%，而IPR 下降了4.4%;低分辨率的本文算法相比高分辨率的IPR 算法，平均精度提高了0.7%。实验表明，本文算法提高了检测精度，降低了时空复杂度。

轻量级人体姿态估计能够有效降低计算资源，是部署到嵌入式设备实际应用的基础。后续研究中，仍需考虑改进主干网络，提高预测精度和效率。