煤巷支护参数预测研究

陈攀， 马鑫民， 向俊杰， 陈莉影， 梁厅皓

（1. 中国矿业大学（北京） 力学与土木工程学院，北京 100083；2. 云南省水利水电勘测设计院有限公司，云南 昆明 650021）

0 引言

巷道是煤矿井工开采的脉络，科学合理的煤巷围岩稳定性控制是保障煤矿安全高效开采的关键[1]。锚杆支护自1956年引入我国至今，得到了广泛的应用，已成为最主要的煤矿巷道支护方式[2]。随着煤矿开采深度、范围和强度的不断增加，巷道支护面临的条件逐渐复杂化，巷道支护设计繁琐、效果差等问题日益突出[3]。

近年来，越来越多的专家学者将计算机智能设计方法应用到煤巷支护领域，利用智能算法来实现巷道支护的合理、科学设计[4]。谢广祥等[5]提出了通过构建多级人工神经网络来确定锚杆支护的方式，优化了支护参数。王茂源[6]采用模糊聚类对围岩稳定性进行分类，采用神经网络算法实现了锚杆支护参数设计。王哲哲等[7]结合模糊理论与人工神经网络构建评价模型，对围岩稳定性进行分级，从而进行巷道支护方案优选。Xu Qingyun等[8]基于人工神经网络预测模型对围岩进行分类，构建了决策系统的支持网络模型，通过数值模拟和现场测试验证了该模型的可行性。Ren Heng等[9]为了评价神东矿区的围岩稳定性，添加动量项来修正BP神经网络的权值，进一步提升了模型精度。Zhang Xiliang等[10]提出粒子群优化（Particle Swarm Optimization，PSO）算法与人工神经网络（Artificial Neural Network，ANN）相结合的PSO-ANN模型来评价和预测巷道稳定性，评价结果表明PSO-ANN模型可准确评估巷道的稳定性。

通过查阅大量参考文献，发现目前支持向量机（Support Vector Machine, SVM）、随机森林（Random Forest, RF）等算法在岩土工程领域取得了很好的应用效果[11-14]，但在煤矿巷道支护领域应用较少。为了全面研究不同的机器学习模型进行支护参数设计的适用性，笔者建立了煤巷支护智能预测数据库，将SVM、ANN、RF、AdaBoost（ADA）和朴素贝叶斯分类器（Naive Bayes Classififier，NBC）5种机器学习方法引入煤巷锚杆支护参数预测中，建立评价体系对模型的性能进行评价，验证机器学习方法在煤巷锚杆支护参数预测方面的可行性。

1 智能算法原理

1.1 SVM

SVM是一种针对小样本数据的机器学习模型[15]。以风险最小化原则将误差风险控制到最小，通过核函数将在低维线性不可分的数据映射到高维空间，使线性内积运算非线性化，从而在高维空间寻找最优分类超平面实现数据线性可分[16]。SVM寻找最优超平面的过程实际上就是支持向量到超平面的间隔D最大化问题。

式中：ω为特征空间中的权向量；c为惩罚系数；i为样本个数，i=1，2，…，n，n为样本总个数；ξi为损失函数。

SVM通过核函数将数据从低维空间转换至高维空间，高斯核函数为空间中任一点xi到某一中心xj（j=1，2，…，n，j≠i）之间欧氏距离的单调函数，可记作K（xi，xj），常被用于高维度、线性不可分的数据。

式中g为高斯核函数参数。

惩罚系数c表征对离群点的重视程度，即模型对错误分类样本的惩罚力度，c越大，惩罚力度越大，容易使模型过拟合；c取值太小，会使模型过于简化，对错误分类的样本学习训练不够，导致模型欠拟合。高斯核函数参数g决定了数据映射到新特征空间后的分布，通过函数的径向范围影响模型的计算速度。因此，惩罚系数c和高斯核函数参数g决定了高斯核SVM模型的整体性能。

1.2 遗传算法（GA）对SVM超参数寻优

传统的SVM只能通过经验或试错法来进行惩罚系数c和高斯核函数参数g的选择，只能寻找到局部最优参数，不能完全将SVM的性能体现出来。遗传算法（Genetic Algorithm, GA）是通过计算机模拟自然界生物进化过程的一种随机化搜索算法，通过对群体中具有某种特征的个体进行选择、交叉和变异操作，生成新的群体，逐渐逼近最优解[17]。

采用GA对SVM的惩罚系数c和高斯核函数参数g进行全局寻优。优化的主要流程如图1所示。GA先对惩罚系数c和高斯核函数参数g进行编码，解空间向编码空间映射；生成初始种群，定义适应度函数并计算个体初始适应度；进行选择、交叉和变异操作，形成新的个体，并计算个体适应度，重复进行这一操作直到满足终止条件；完成解码，获取最佳参数cbest和gbest。

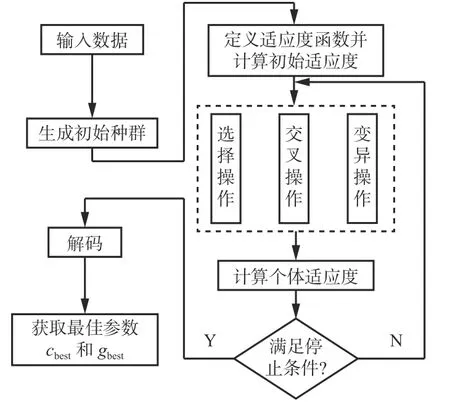
图1 GA对SVM超参数寻优流程Fig. 1 GA optimization process for super parameters of SVM

2 煤巷支护数据库建立

2.1 评价指标的选取

根据巷道支护设计的需要，选择顶板锚杆和帮部锚杆的直径、长度、间距、排距和数量，将顶板锚索的直径、长度、数量和布置方式作为输出参数，其中布置方式是锚索排距对顶板锚杆排距的倍数。煤矿巷道锚杆支护的影响参数涉及广泛且复杂，将所有的参数都输入到机器学习模型中容易加大模型的复杂度，导致模型过度拟合而失去泛化性，因此，对机器学习模型的输入参数进行精选十分必要。选择影响参数时遵循获取方便、可量化、物理意义明确、独立性、普适性等要求，综合我国目前的煤巷生产情况和锚杆支护理论，从围岩参数、围岩节理裂隙发育程度和巷道埋深及断面尺寸3个方面选出12个参数作为机器学习的输入参数。

1） 围岩参数。对煤矿巷道进行支护的根本目的是保持巷道畅通和围岩稳定，降低围岩移动量，改善围岩力学性质。由此可见，围岩参数对巷道变形与破坏的影响十分显著。本文选择煤层、基本顶、直接顶及直接底的厚度和强度表征巷道围岩特性。

2） 围岩节理裂隙发育程度。在围岩内部存在的节理、裂隙、层理等构造对岩体的整体强度存在不同程度的影响，一般情况下，节理、裂隙多的岩体完整性较差，锚杆、锚索对岩体稳定性的影响很大。

3） 巷道埋深及断面尺寸。巷道埋深和断面尺寸对围岩支护有重要影响。垂直应力随着巷道开采深度的增加而逐渐增大，高地应力情况下围岩更易发生塑性破坏，保持围岩稳定性更加困难。另外，巷道的宽度和高度对围岩稳定性的影响也不可忽视。

2.2 数据采集与处理

1） 数据采集。为了保证煤巷支护数据的丰富性和数据来源的可靠性，采用现场调研、问卷调查和文献检索等方式收集2010—2022年的典型煤巷支护数据，共157条。

2） 缺失值填补。在数据收集的过程中，无可避免地形成少量的数据缺失，在进行数据分析前参照相同矿场类似的巷道对缺失值进行填补。

3） 离群点处理。为了让样本满足机器学习模型训练和测试要求，需统一数据的整体分布。通过数据箱形图找出在样本中出现明显偏离大多数观测值的个别值，如图2所示。上四分位数加上1.5倍的四分位距为上限，下四分位数减去1.5倍的四分位距为下限，在上下限之外的点判定为离群点，采用三角形将离群点标出来，并采用极值化处理离群点：偏大值修改为箱形图极大值，偏小值修改为箱形图极小值。

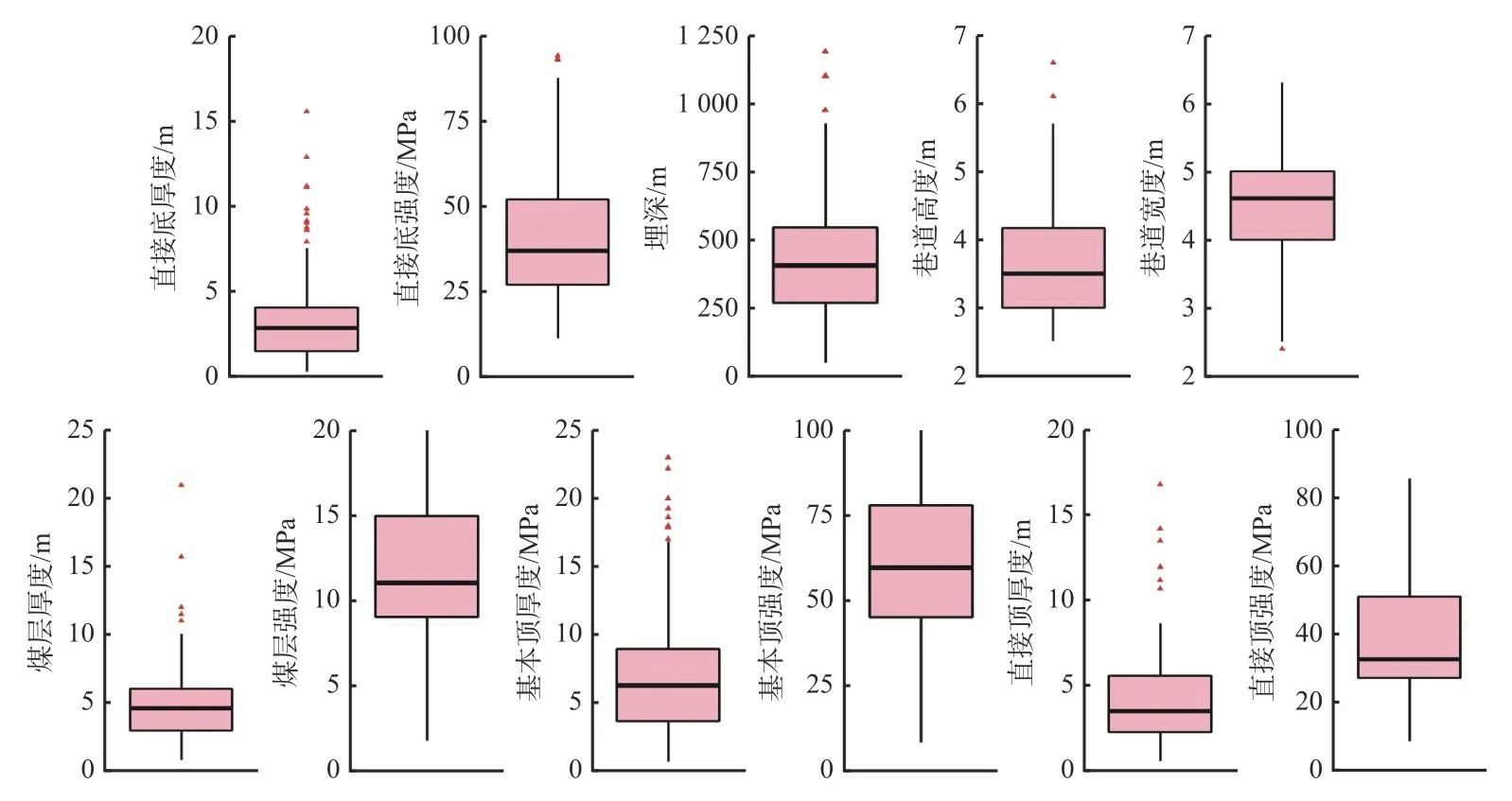
图2 原始数据的箱形图Fig. 2 Box diagram of the original data

4）异常样本剔除。采用局部异常因子（Local Outlier Factor，LOF）对数据离群样本进行检测[18]。LOF是一种基于样本局部密度检测识别离群样本的经典算法，通过计算样本点的局部密度量化每一个样本点的异常程度，样本点的异常程度取决于样本点与周围点的局部密度比较。LOF算法步骤：① 计算样本点p的第k距离领域，即与点p相距最近的k个点的集合。② 计算点p与点p的第k距离领域内各点的可达距离，其中，点p到点o的可达距离为点o的k邻近距离和点p与点o之间的直接距离的最大值。③ 计算点p的局部可达密度，即样本点p与它的第k距离领域内各点的平均可达距离的倒数。④ 对每个点的第k局部可达密度进行比较并排序。样本点的第k局部可达密度越大，表明它的异常程度越小，反之，异常程度越大。

在不同k值下使用LOF算法进行7次检测，取每个k值下异常程度最高的10个样本，结果见表1。7次检测中出现次数不少于4的样本被确定为异常样本。可看出10个异常样本为33，84，105，124，151，75，14，129，25，109，将10个异常样本被剔除，剩余147个样本组成煤巷支护智能设计数据库。

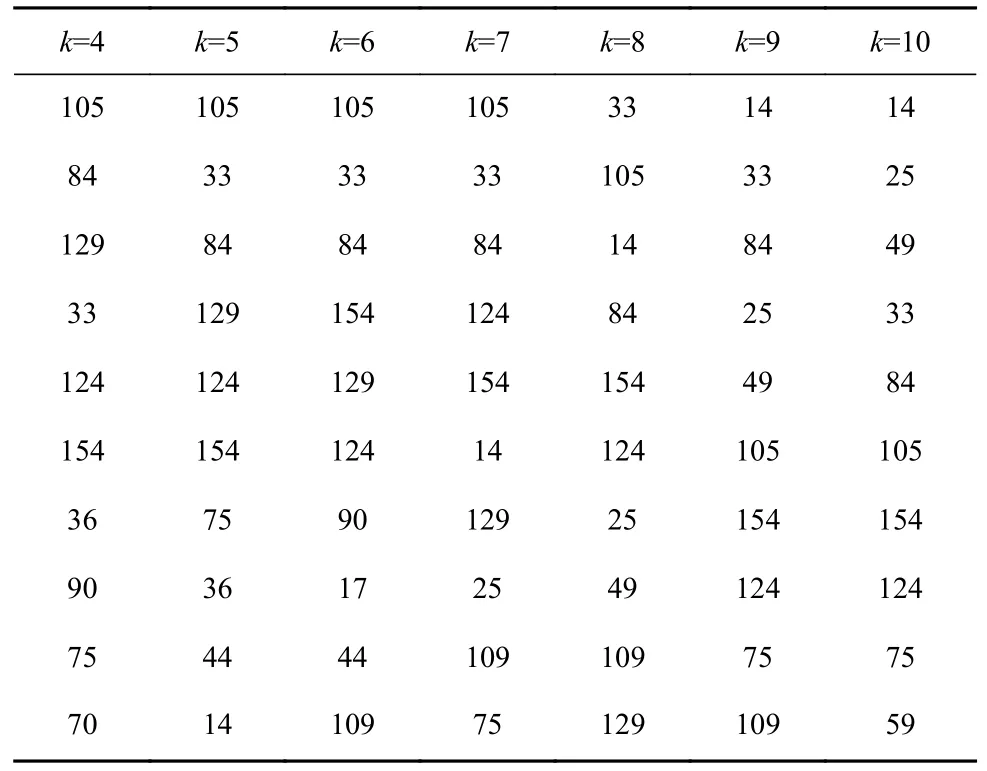
表1 基于LOF的异常样本检测结果Table 1 Test results of abnormal samples based on local outlier factor(LOF)

2.3 合成少数类过采样技术（SMOTE）平衡样本

为便于模型的学习训练和测试，从数据库中随机抽取80%（117组）的数据作为训练集，剩余20%（30组）的数据作为测试集。训练集中各支护参数的频数统计结果见表2、表3和表4，各输入参数的分布统计情况如图3所示。

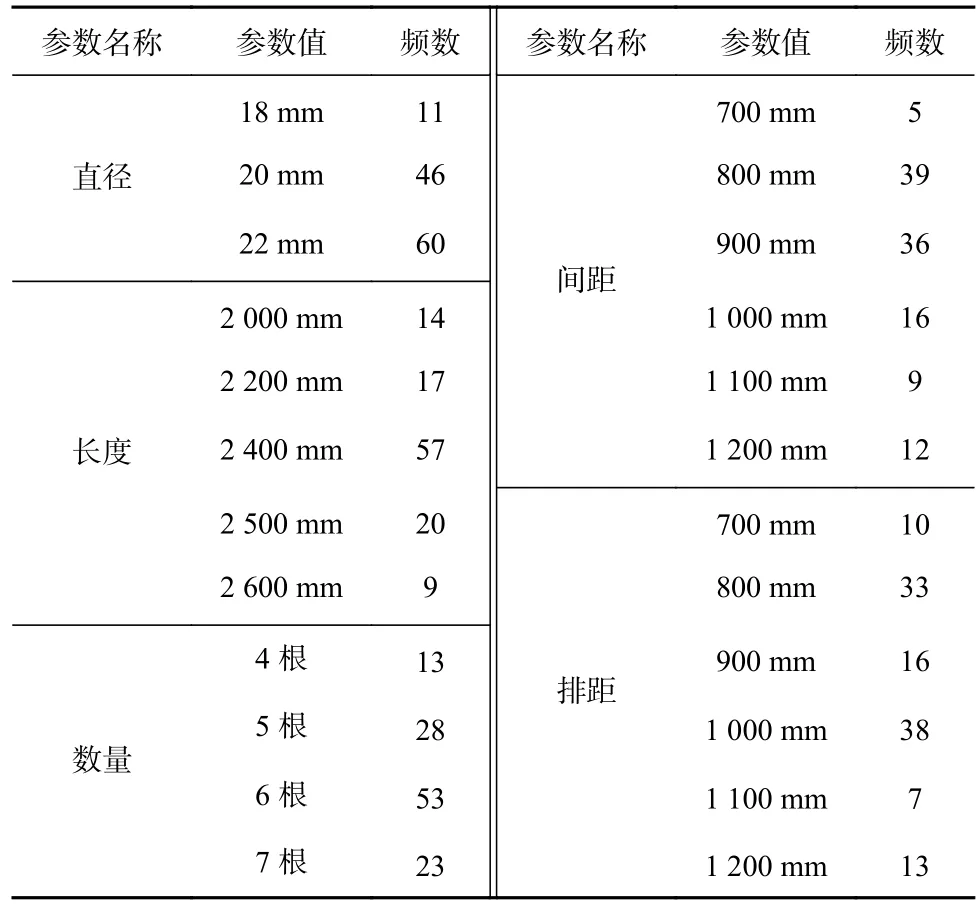
表2 顶板锚杆支护参数统计Table 2 Statistics of roof anchor bolt support parameters

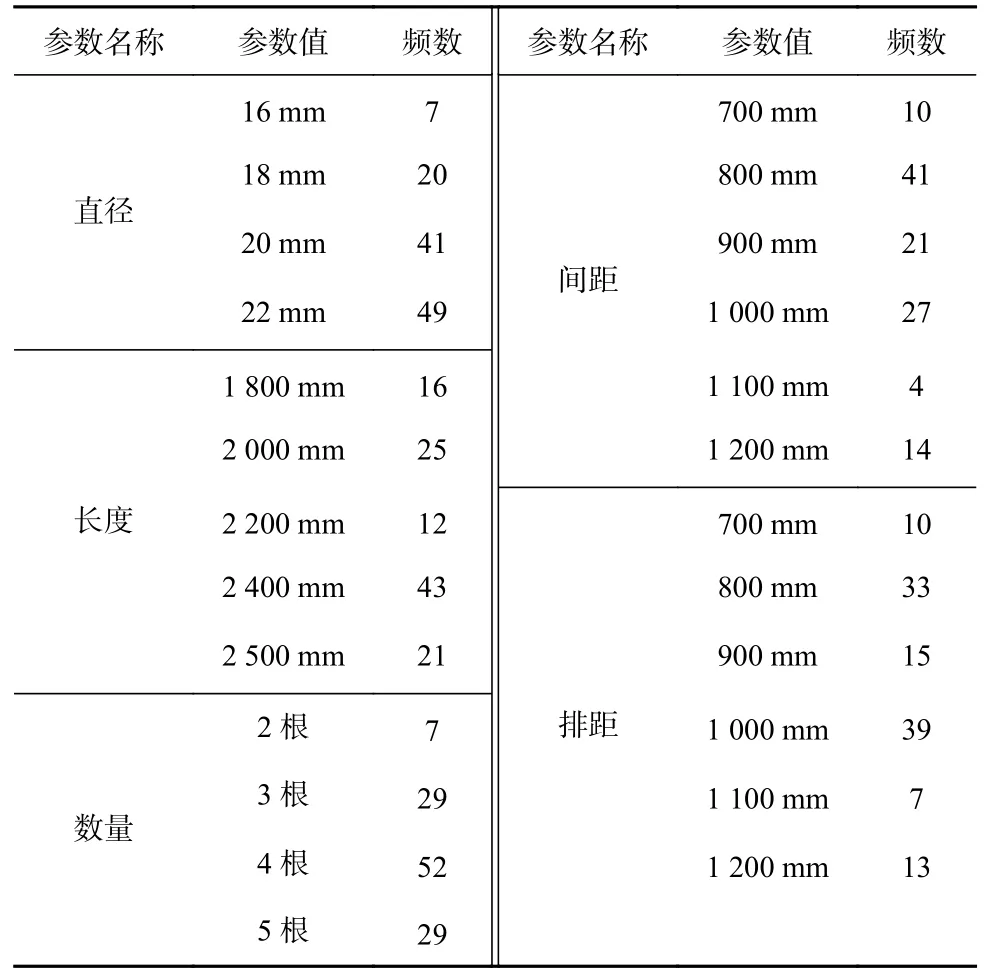
表4 帮部支护参数统计Table 4 Side support parameter statistics

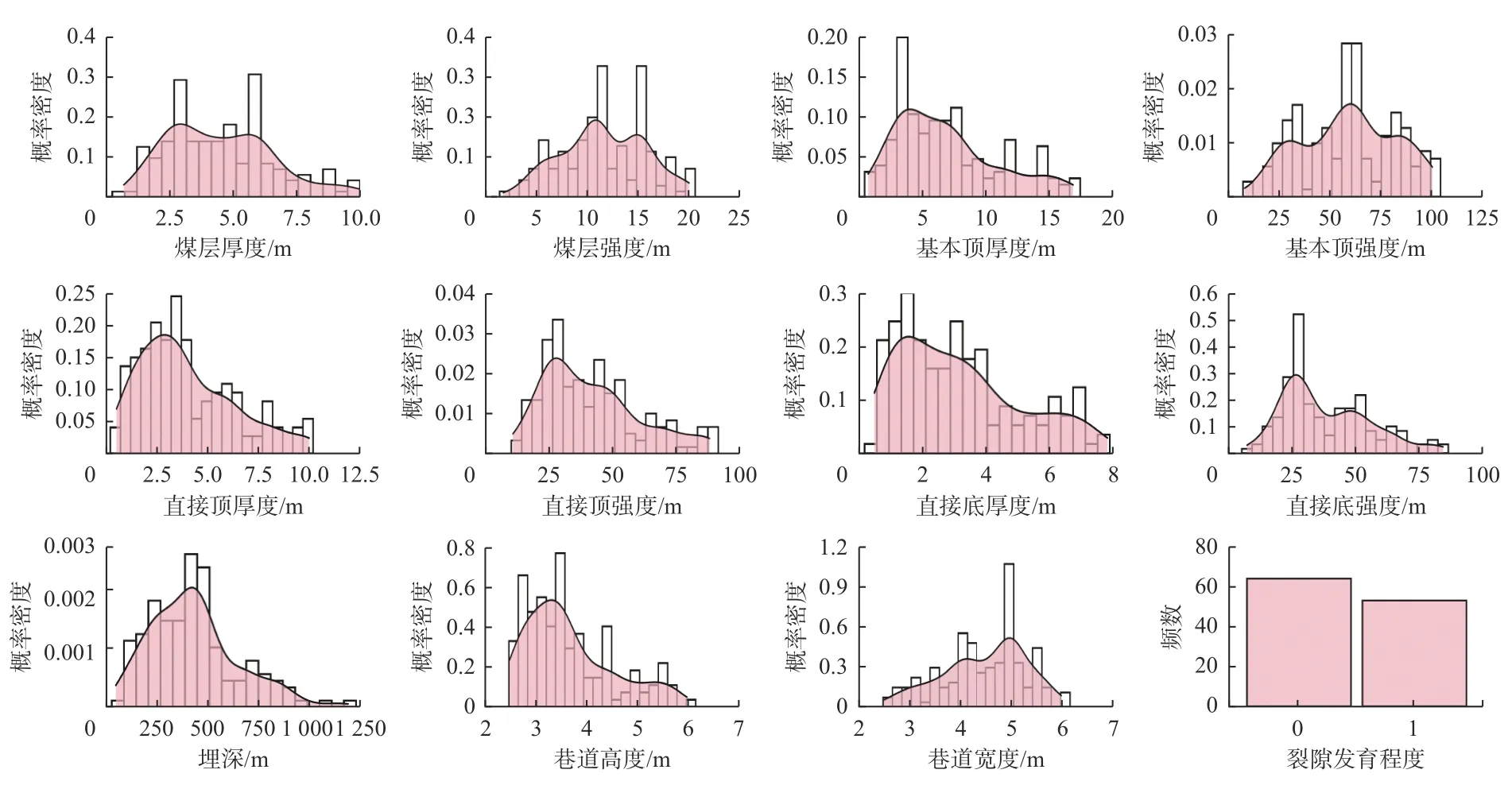
图3 训练集输入参数分布统计Fig. 3 Distribution statistics of input parameters of training set

由表2、表3和表4可知，支护参数是不均衡的类分布，存在某一类或某几类样本数量显著少于其他类别的情况，这会降低模型对少数样本的拟合。采用SMOTE对数据进行类平衡处理。SMOTE是基于随机过采样算法的一种改进方案，若2个同类样本间的欧氏距离足够近，则SMOTE假设这2个样本之间的样本与这2个样本同类[19]。SMOTE平衡样本流程如图4所示。根据样本不平衡比例确定采样倍率b；随机选取一个少数类样本X，计算与其他样本间的欧氏距离，并找出样本X的k个同类近邻样本；在每个少数类样本X的k个同类近邻样本中随机选取一个样本m；在m和X之间的连线上随机选取一个点作为新的少数类样本X′，重复以上步骤，直到少数类样本满足采样倍率b，输出最终的数据集。

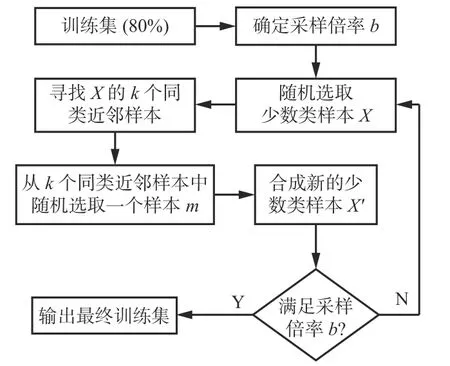
图4 SMOTE平衡样本流程Fig. 4 Sample balancing flow by SMOTE

式中r（·）为随机函数。

2.4 数据标准化

最终训练集中的各个特征向量具有不同的量纲和单位，采用Z-score标准化方法将数据转换为均值为0、标准差为1的数据。采用式（4）对最终训练集进行处理。

式中：y为标准化后的值；ai为特征值；为特征均值。

煤巷支护数据库的整体流程如图5所示。首先通过现场调研、问卷调查和文献检索等方式收集煤巷支护技术资料；然后采用缺失值填补、离群点处理及异常样本剔除等方式对数据进行清洗处理，建立煤巷支护数据库；最后按照8∶2的比例将数据库中的数据分成训练集与测试集，并采用SMOTE平衡训练样本，经标准化处理后即可用来训练和测试模型。

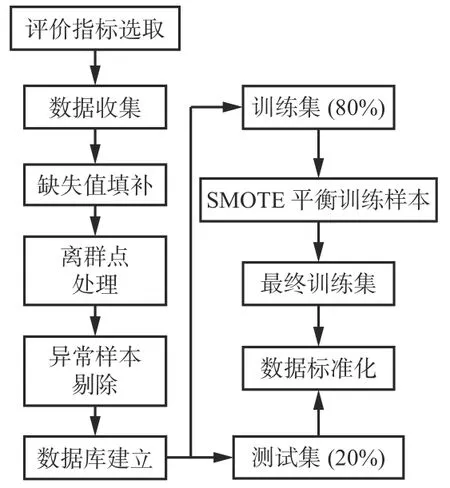
图5 煤巷支护数据库的整体构建流程Fig. 5 The overall building process of the coal roadway support database

3 煤巷支护参数预测模型建立与评价

3.1 SMOTE-GA-SVM模型

选用GA算法对SVM参数进行全局寻优[20]。GA参数设置：种群规模为50，直接复制到下一代的染色体数量为20%，交叉概率为0.8，变异概率为0.01，繁殖次数为300，采用精确度作为模型适应度函数。设置惩罚系数c和高斯核函数参数g的寻优范围分别为[0，10]和[0，200]。GA生成初始群体并计算初始适应度，然后通过选择、交叉、变异等操作，经过设定繁殖次数或个体适应度满足要求后终止计算，将得到的最大适应度作为全局最优解输出。通过GA优化后，确定各模型的最佳超参数组合cbest和gbest，结果见表5。

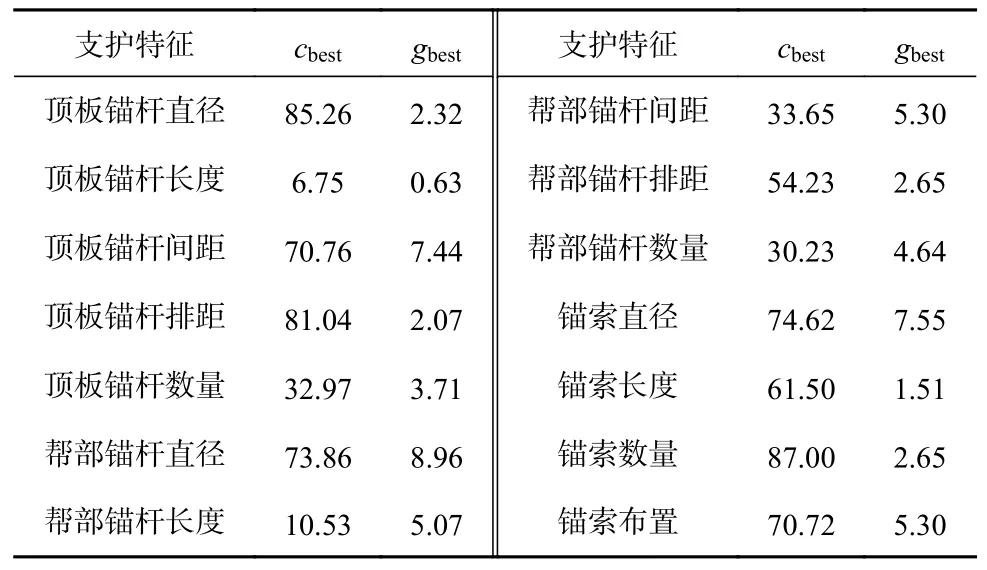
表5 GA全局寻优结果Table 5 Global optimization results of GA

SMOTE-GA-SVM支护参数预测模型建立流程如图6所示。

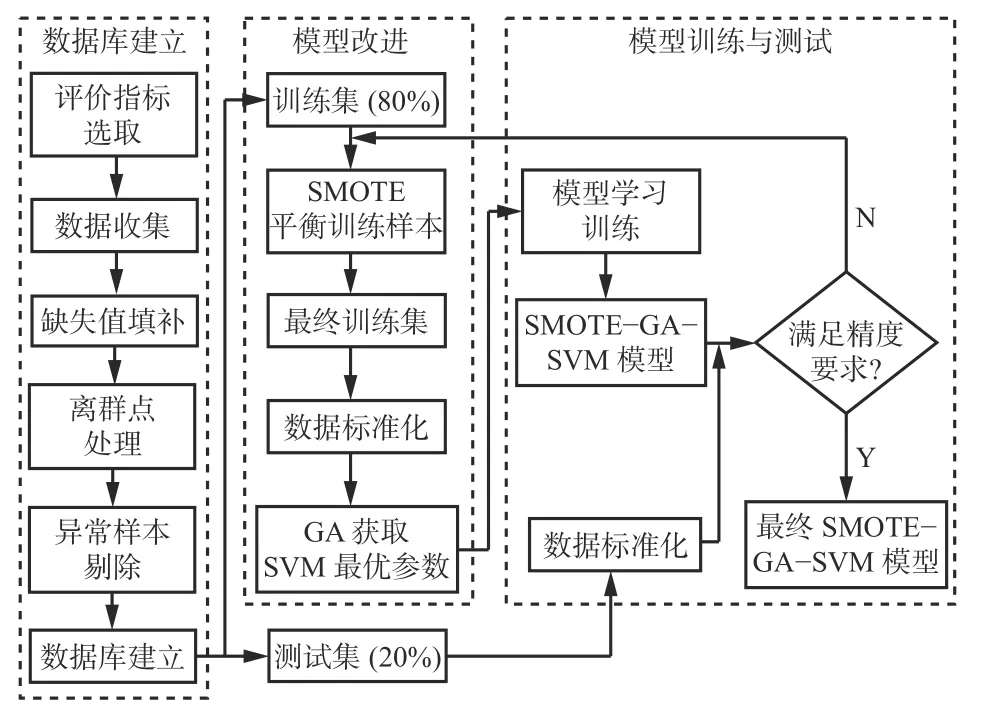
图6 SMOTE-GA-SVM支护参数预测模型建立流程Fig. 6 SMOTE-GA-SVM supporting parameter prediction model establishment process

首先建立煤巷锚杆支护数据库；然后通过SMOTE平衡样本、数据标准化和GA超参数寻优等步骤优化改进SVM支护参数预测模型的性能；最后经过模型训练和测试建立满足精度要求的SMOTEGA-SVM支护参数预测模型。

3.2 RF模型

RF是一种集成学习算法，因其优越的性能成为一种流行的分类算法[21]。RF的树构建过程允许特征之间的交互作用和高度相关性，可量化输入变量对于模型的重要程度。各指标对支护设计的重要程度排序如图7所示。可看出裂隙发育程度是最重要的指标，直接底厚度对模型的贡献度最小，这为支护设计时的变量选择提供了参考。

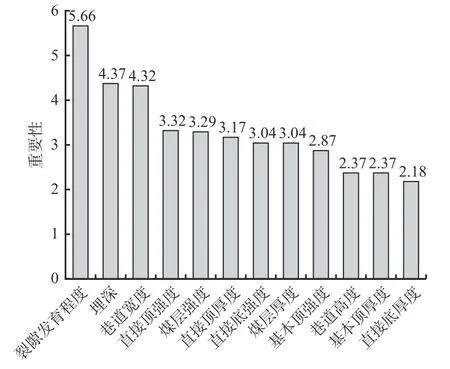
图7 输入变量在支护参数预测模型上的重要性Fig. 7 Importance of input variables in support parameter prediction model

3.3 GA-ANN模型

ANN是应用最为广泛的机器学习算法之一，输入层、隐藏层和输出层共同组成了ANN结构，其中，输入层和输出层的结构由模型的输入参数和输出参数决定，不可改变，调整隐藏层的结构能显著改变模型的性能。通过试错法确定了隐藏层结构为9-7时模型性能最好。为了提高网络性能，采用GA对ANN的权重和偏差进行优化。其中，GA参数设置与SMOTE-GA-SVM模型一致。另外，ANN模型采用支持回溯的弹性反向传播算法，设置误差学习率为0.01，以Sigmoid函数作为激活函数，模型最大迭代次数为1 000。同时，对模型进行10倍交叉验证，每次模型的初始权重都不一样，一定程度上避免出现局部最优解。构建的顶板锚杆间距GA-ANN预测模型的网络拓扑结构如图8所示，其中，I1-I12为输入指标，H1-H9为隐藏层神经元，O为输出层，B为偏差，线条颜色和粗细分别代表不同的权值和偏差。

3.4 ADA模型和NBC模型

ADA是在Boosting基础上的一种优化算法。ADA在面对多分类问题时，通过不断调整错误样本的权重迭代升级，一定程度上避免了模型过拟合。

NBC算法是一种采用最大似然估计对样本进行概率分类的算法，通过求解样本在各个类别下的概率进行求解。

3.5 模型性能评估

采用分类精度来评价支护参数预测模型在测试集上的性能，分类精度为模型在测试集上正确分类样本数与总样本数的比值。建立的所有机器学习模型在测试集上的分类精度见表6。可看出SMOTEGA-SVM模型的表现最佳，每一个支护参数的分类精度均超过75%，模型平均分类精度达到83.8%。ADA模型在预测帮部锚杆间距时表现最差，分类精度只有37.6%；SMOTE-GA-SVM模型预测锚索长度时表现最佳，分类精度达到93.5%。SMOTE-GA-SVM模型在处理样本类不均衡数据集的问题上性能更加强大，平均分类精度较传统的SVM模型提高了21.8%。在SMOTE和GA的优化改进下，SVM模型整体性能有了较大提高。可见，SMOTE方法可作为处理样本类不均衡的有效方法，GA对SVM模型的超参数有很好的全局寻优能力。且SMOTE-GA-SVM模型优于其他模型，平均分类精度达83.8%；ADA在测试集上的性能最低，精度为60.5%。预测模型分类精度排序为SMOTE-GA-SVM、RF、GA-ANN、SVM、NBC、ADA，6种模型的平均分类精度达69.9%。

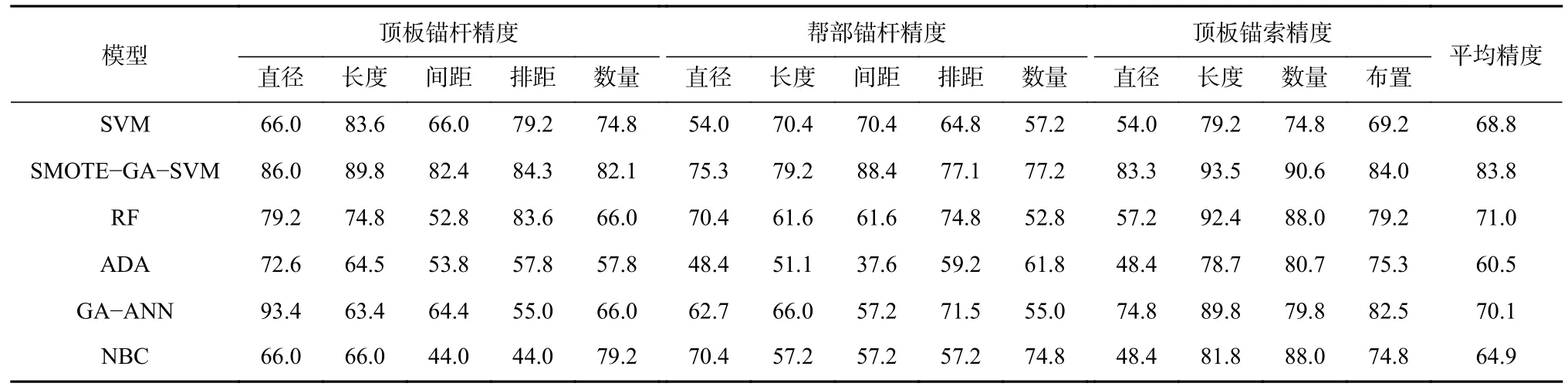
表6 机器学习模型在测试集上的分类精度Table 6 Classification precision of machine learning model on test set%

4 工程应用

为了验证基于SMOTE-GA-SVM的煤巷支护参数预测模型在工程实践中的适用性和可靠性，在山西霍宝干河煤矿的4条巷道进行了实际工程验证，巷道的特征参数见表7。对巷道特征参数进行Z-score标准化，并将其输入已经建立好的基于SMOTEGA-SVM的煤巷支护参数预测模型中，通过模型计算得到巷道的锚杆、锚索支护参数，结果见表8。

表7 霍州矿区干河煤矿的特征参数Table 7 Characteristic parameters of Ganhe Coal Mine in Huozhou Mining area

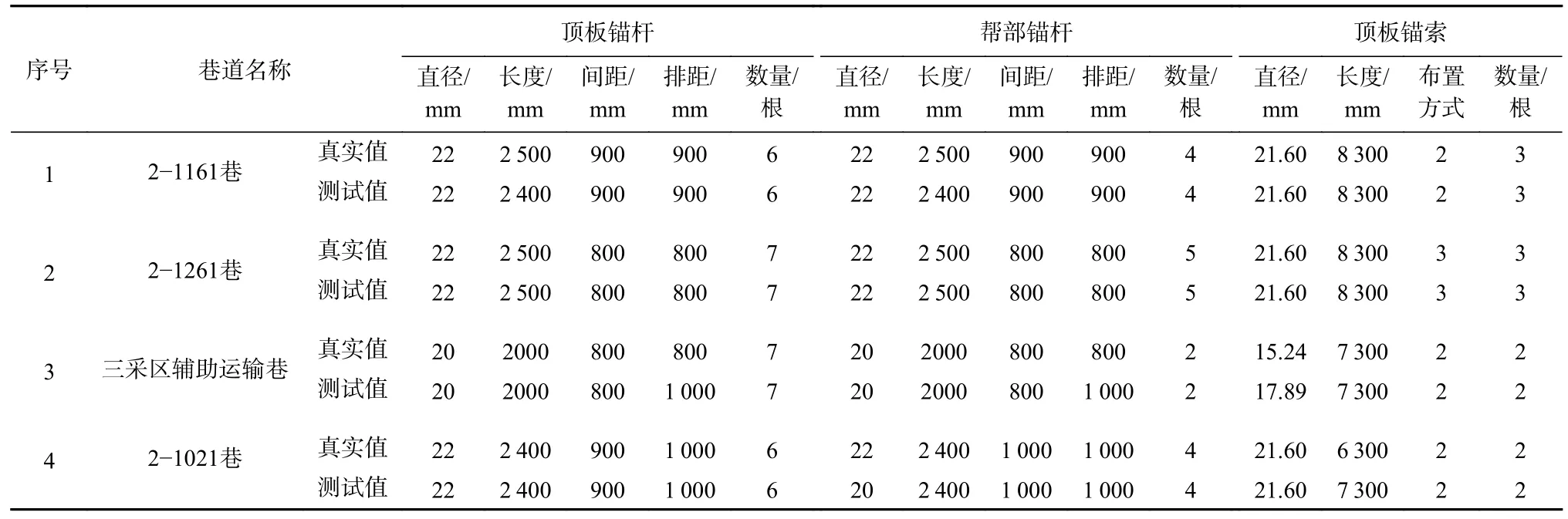
表8 SMOTE-GA-SVM模型应用结果Table 8 Application result of SMOTE-GA-SVM model

由表8可知，2-1261巷实际采用的锚杆、锚索支护参数与SMOTE-GA-SVM模型计算结果一致，2-1161巷和2-1021巷都有2个参数预测错误，三采区辅助运输巷有3个参数预测错误，4条巷道的56个支护参数中预测结果与真实值相同的有49个，模型预测的正确率为87.5%。其中，SMOTE-GASVM模型错误预测的7个参数都被预测为相邻类别的参数，相对误差较小。由此可见，SMOTE-GASVM模型能够很好地掌握巷道特征参数到锚杆、锚索支护参数的非线性映射能力，具有较强的适用性和可靠性，对煤巷锚杆、锚索支护参数设计具有一定的参考价值。

5 结论

1） 建立了煤巷支护智能预测数据库。采用现场调研、问卷调查和文献检索等方式收集煤矿巷道样本；采用缺失值填补、箱形图修改离群点和LOF剔除异常样本等方式对数据进行处理后，建立煤巷支护智能预测数据库。

2） 提出一种基于SMOTE-GA-SVM的煤巷支护参数预测模型，该模型在训练前采用SMOTE方法平衡训练集中类别不平衡的样本，提高模型对少数类样本的拟合能力；训练过程中使用GA对超参数进行全局寻优，进一步提高了模型整体性能。测试结果表明，基于SMOTE-GA-SVM的煤巷支护参数预测模型的分类精度达83.8%，比传统的SVM模型提高了21.8%。

3） 将ANN、RF、ADA和NBC引入煤巷支护参数预测中，建立对应的支护参数预测模型。结果显示，从最优到最差的预测模型排名分别为SMOTEGA-SVM、RF、GA-ANN、SVM、NBC和ADA，验证了机器学习方法在煤巷支护参数预测方面的可行性。

4） 在山西霍宝干河煤矿的4条巷道对SMOTEGA-SVM模型进行了应用，模型预测准确率达到87.5%，具有较强的适用性和可靠性。