基于数据修正的概率稀疏自注意短期风电功率预测

施进炜，张 程，2，原冬芸

（1.福建理工大学电子电气与物理学院，福建福州 350118；2.智能电网仿真分析与综合控制福建省高校工程研究中心，福建福州 350118；3.闽江学院材料与化学工程学院，福建福州 350108）

0 引言

近十年来，可再生能源风能经历了阶段式的跨越，截止到2022 年，全年风光发电累计装机容量达到7.6 亿千瓦，同比增速达18.75%，风电已经逐步成为能源供应的中坚力量。但由于风力发电受气象和和地理条件的影响，风电具有随机性、波动性和间歇性，使得大规模的风电并网电力供需难以平衡[1-4]。提高风电预测的精度，有助于优化电网的整体规划调度，找到风机的最佳组合，保证电力系统安全稳定运行，从而进一步提高风电的经济效益[5-7]。因此风电功率预测技术的精准度是当前探究的重要方向。

目前为止，风电功率的预测法分为统计法和物理法[8]。而物理法主要是用数值天气预报（Numerical Weather Prediction，NWP）的预测结果得到气象数据，再利用风机的功率曲线计算得出风机的实际输出功率。NWP 更新的频率在1～3 h 内，不适用于短期风电功率预测。而统计法则是基于历史风电功率数据，结合输入特征信息构建功率预测的非线性模型，主要包括时间序列模型[9]、支持向量机模型[10]、深度神经网络模型[11]等。

随着深度学习的不断发展，通过学习大量参数，非线性的数据拟合能力得到不断地提高。因此，使用深度神经网络来拟合风电功率这种具有强随机的时间序列具备合理性[12]。长短期记忆网LSTM[13]（Long Short Term Memory，LSTM）和门控循环单元[14]（Gate Recurrent Unit，GRU）为主的神经网络在风电功率预测中有大面积的应用。文献[15]中长短期记忆模型构建高频校正模型，弥补低频分量缺失的高频分量，提高数据挖掘的准确性。文献[16]对天气预报、实测功率数据进行时空特征提取，结合注意力机制，对多个风场之间相关性进行学习，剔除低权重冗余信息。获取预测精度更高的风电功率未来数据。文献[17]采用动态权重选择、孤立森林算法以及邻近节点算法筛选并处理数据，构建多元注意力框架，具有提高模型预测精度的作用。Transformer 模型完全抛弃常见的循环神经网络RNN（Recurrent Neural Network，RNN）、LSTM 结构，采用Encoder-Decoder 结构，最近许多学者将其运用到序列数据预测领域均取得了不错的效果[18]，但其计算复杂度高，多层网络堆叠，占用内存，训练速度较慢。

采集过程中不可控因素的存在，使采集到的原始风电数据中存在异常数据及缺失数据[19]，无法进行直接预测。文献[20]将离群信息标识为异常，但该方法流程较复杂，且检测耗时过长。文献[18]虽然检测精度高，但受参数选取的影响大，因此鲁棒性较差。文献[21]采用基于距离的异常检测，但需提前获悉数据的先验知识且无法对数据的异常度进行区分。

本文提出一种数据修正的概率稀疏自注意力风电功率预测方法。首先，采用一种新的集成异常检测技术，通过综合K 近邻、局部异常因子、孤立森林3 种方法进行异常检测，并且利用轻梯度提升机（Light Gradient Boosting Machine，lightGBM）学习经过清洗的风速-功率数据集，对缺失值进行补充。然后将修正后的数据集输入Informer 模型进行训练，该模型通过概率稀疏自注意（ProSparse selfattention）筛选出重要特征，在保证预测精度的基础上，进一步提高运算速度。此方法能提高预测效率和精度，准确的短期风电功率预测有助于减少电力系统的调峰负荷，降低火电厂的启停次数，提高火电厂的运行效率，降低运行成本。而更高效率的预测，可以更快地为电网调度提供可靠的信息，提高电力系统运行的经济性和稳定性。

1 短期风电功率预处理

1.1 风电数据集分析

本文采用的风电数据集来源于某风电场。该数据集记录了风电场从2019 年3 月1 日00：00—2020 年2 月28 日24：00 的70 m 高度的风速、风向、环境温度、实测风电功率等数据，采样时间间隔为15 min。

图1 为该风电场四季的风力玫瑰图，受季节影响，春夏盛行的东风，秋季从东风向西南风过渡，冬季盛行西南风。

图1 四季风力玫瑰图Fig.1 Dynamic wind rose for four seasons

1.2 异常检测模型

根据风速-风电功率的数据分布特征，正常的数据分布在风速-风电功率曲线附近，然而异常数据常表现为横向数据带聚集性分布且明显偏离风速-功率曲线。如图2所示。

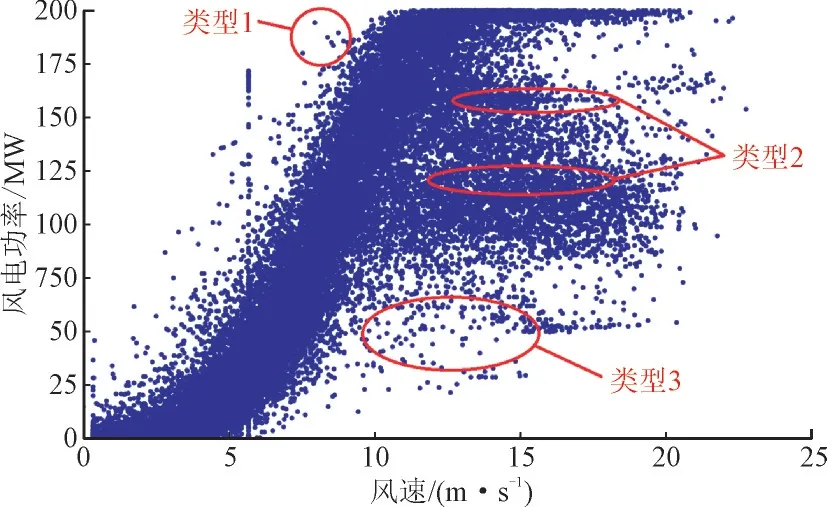
图2 异常数据类型Fig.2 Abnormal data type

异常类型主要分为3 类：（1）类型1：曲线上部分的堆积式异常数据，一般由计量装置的失灵所引起；（2）类型2：曲线中部的堆积式异常数据，一般是由限电或网络故障引起；（3）类型3：曲线周围分散式异常数据，一般是由于气象波动、信号传播噪声等随机情况造成。

1.2.1K近邻聚类检测

K近邻（K-Nearest Neighbor）是一种常用的监督学习方法，其工作机制是随机选定初始样本作为起点，计算各个样本与所选起点的欧式距离来判断相似程度，即相似分数[22]。根据相似分数去划分类别，随后确定各类别中心。重复上述步骤，直到起点不改变，划分的样本类别就确定完毕。

1.2.2 局部异常因子检测

局部异常因子检测（Cluster-based Local Outlier Factor）首先通过k-means 聚类，区分出大簇和小簇[23]。然后将每簇按数据量从大到小排序之后，大簇通常占总量的90%左右，余下的就被认为是小簇。最后计算异常点分数，当数据点属于大簇的时候，计算它与当前簇的聚类中心的距离，当数据点属于小簇时，计算它与最近的大簇的聚类中心的距离，得出异常分数，然后从大到小排序，筛选出异常值。

1.2.3 孤立森林异常检测

孤立森林（Isolation Forest）算法是一种无监督离群点检测算法，该算法不使用距离或密度测度来检测异常，而是根据所计算出样本点的异常分数来识别其中的异常点[24]。孤立树林计算法首先计算每个数据的原始异常得分，然后根据孤立树在样本空间P中随机选取m个特征，在所选取数据的最大值与最小值间随机选取一个数值，以分割数据点。随着观测数据的划分递回的重复，直至把所有的观测值都孤立，然后再把各个树组成孤立树林。

对于样本点的异常值分数S(x)定义如下：

式中：h(x)为样本点x在森林中的平均深度；c(n)为由n个点构造的孤立树的平均路径长度，计算方法如下:

式中：H(g)为谐波函数，H(g)=lng+0.58

1.2.4 KCI集成异常检测

集成近邻森林异常检测算法（Nearest-Cluster-Isolation，KCI）是一种基于多种检测算法的集成异常检测。该算法利用近邻算法、孤立森林、局部异常因子检测分别检测异常点。在理论功率曲线小波动范围内，筛选掉所检测的异常点，最后综合3个算法检测的结果合并为异常点集合，步骤为：

1）标记历史风速-功率数据集合所有样本为初始未处理状态。

2）输入3 种异常检测算法种，分别判断出每个样本点是否为异常值，输出3 个异常点集r1，r2，r3。

3）3 个异常点集通过选择门w，即计算异常点与理论功率曲线的横向距离是否在理论功率的±5%内，若异常点被识别在该范围内，则剔除此异常点。

4）综合筛选后的异常点集，输出异常点集合。

1.3 缺失值重构

异常值清洗之后，原始数据序列存在数据缺失，会破坏风电数据集在时序上的连续和完整，进而导致数据分析挖掘变得困难。因此需要对缺失值进行重构，才能保证数据质量。针对该问题本文采用LightGBM[25]，对清洗后的数据进行深度学习，生成的新的数据来重构数据集，以此来对缺失的功率值进行补充。

LightGBM 是一种高效的梯度增强决策树，其本质是多个弱回归树的加法模型，是梯度提升决策树GBDT（Gradient Boosting Decision Tree）[26]的升级版本，可以有效地解决高维大量数据处理效率较低的问题。采用互斥特征捆绑、单边梯度采样和高效并行新技术，减少了特征数量，避免小样本数据的影响，有效减少特征数量，提高效率和准确度。

图3 为单棵回归树的结构。LightGBM 采用leaf-wise 策略，每次对所有叶子分裂增益最大的子节点进行分裂，其他叶子节点则不会分裂。为了避免出现过拟合，LightGBM 会限制叶子节点生长过程中树的深度，即调节max_depth 来限制树的深度。

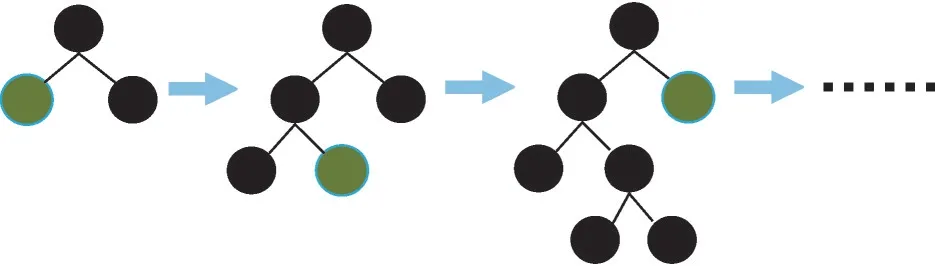
图3 单棵回归树结构Fig.3 Structure of single regression tree

2 短期风电功率预测

Informer 算法是一种高效的基于transformer[27]的时间序列预测模型。针对Transformer 模型的不足，Informer 采用概率稀疏自注意（ProbSparse Selfattention），能够有效降低计算复杂度。编码器和自注意蒸馏（Self-attention Distilling）结合，减少维度和网络参数量。

该算法的结构框架如图4 所示，其中Xen为编码器的风电历史长序列输入，Xdn为解码器序列输入，Xsn为预测点之前的已知序列，X0为预测序列的占位符（将标量设置为0）。左半部分编码器接受大量风电历史长序列输入（紫色系列），采用概率稀疏自注意代替了常规自注意力，粉色梯形是自注意力蒸馏机制；右半部分解码器接收长序列输入，将目标元素置零，测量特征图的加权注意力组成，并立即以生成方式预测输出元素（黄色系列）。

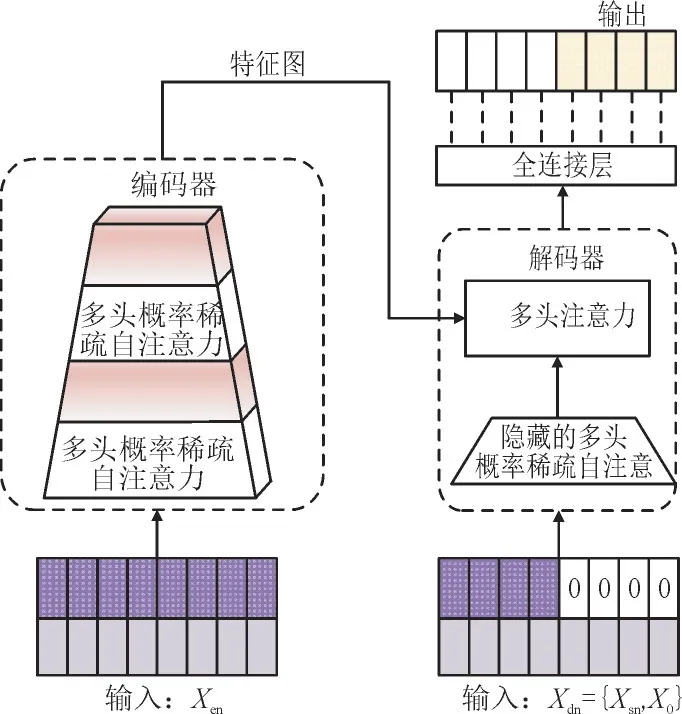
图4 Informer模型框架Fig.4 Informer model framework

2.1 概率稀疏自注意

传统的自注意力机制由Q，K，V（向量）构成，表达式为：

式中:Q为查询向量（query）；K为键向量（key）；V为值向量（value）；d为输入维度。

设qi，ki，vi分别代表Q，K，V中的第i行。第i个查询的注意力被定义为概率形式的内核平滑器：

式中:k(qi,ki)为计算qi，ki的不对称指数核；为第i个Q的条件下K的分布期望值；vj代表V中的第j行。

传统的自注意需要较大内存和二次点积计算代价，是其预测能力的主要缺点。为了保证不遗漏重要注意力且较小的计算量，通过相对熵（relative entropy）定义第i个概率稀疏度量M(qi,K)为：

第一项是所有键向量上qi的对数求和指数函数（log-sum-exp，LSE）；第二项则是他们的算数平均。其中，LK为键向量K中的键数，Kj为K中的第j个键向量。然而这样计算LSE 存在潜在的数值稳定性问题，通过近似qi的方式设定M值的上限：

基于式（6）的理论，提出概率稀疏自注意机制，其表达示为：

式中：和Q为具有大小相同的稀疏矩阵，且仅包含在稀疏度量下的qi中。

算法复杂度用O(L)表示，L为输入数据的量，L的规模越大，算法的执行效率越低。该方法使得计算复杂度从O(L2)降到O(LlnL)。

2.2 自注意蒸馏机制

为了更高效地使用内存和提高运行效率，通过自注意力蒸馏机制逐次将序列长度减半，第j层到第j+1层的蒸馏操作的表达式为：

2.3 短期风电功率预测方法流程图

基于数据修正的概率稀疏自注意短期风电功率预模型流程如图5 所示。

图5 基于数据修正的概率稀疏自注意短期风电功率预测流程图Fig.5 Flowchart of short-term wind power prediction based on data correction with probabilistic sparse selfattention

3 实例分析

3.1 模型参数选择及调优

本文采用自动超参数优化Optuna 对LightGBM进行参数调节，以得到较好的缺失值重构效果，部分关键参数见表1，其中最大深度、正则化系数α、正则化系数β无量纲。

表1 Optuna算法参数调节结果Table 1 Parameter tuning results with Optuna algorithm

Informer 参数设置如表2 所示。其中n_heads为多头注意力机制中的头数，无量纲；seq_len 为控制模型输入序列长度；e_layers 为encoder 的层数；d_layers 为decoder 的层数；loss 为损失函数的类型选择；moving_avg 为移动平均的窗口大小，无量纲。该参数用于控制模型的平滑程度，即在预测时对历史数据进行平滑处理，以减少噪声和异常值的影响。

表2 Informer参数设置Table 2 Parameter settings for Informer model

3.2 异常检测模型对比

为了对风电数据集进行有效充分的修复，采用二阶段的修正策略。在第一阶段，将风电场数据集采用KCI 集成检测进行异常值识别，并与KNN 近邻、局部异常因子检测、孤立森林进行实验比对。在进行无监督异常检测前，将上述4 种方法的污染比例设置为0.05，该参数用来将连续的异常分值转化为0（正常点）和1（异常点）的。

由图6（a）可以看出，KNN 近邻聚类方法在进行风速-功率异常检测时，类型2 并未得到有效识别，散点图中部有密集的异常点堆积。图6（b）显示在异常检测时，该方法仅将类型2 进行正常识别，但类型1 和类型3 并未得到有效的识别。如图6（c）显示孤立森林异常检测能够对类型1 和类型3 进行充分识别，但是类型2 仍识别不够充分。图6（d）显示与其他算法相比，KCI 能够较为充分地识别3 类异常值。

图6 4种异常检测算法结果对比Fig.6 Comparison of results among four anomaly detection algorithms

为保证数据集的完整性，第二阶段对异常值进行清洗后，用LightGBM 对缺失值进行补充，防止后续的数据挖掘出现问题。图7 为经过清洗和重构两步预处理之后的风速-功率曲线，该曲线保留原有的样本趋势下，更加贴近理论风速-功率曲线。

图7 清洗重构后的风速-功率曲线Fig.7 Wind speed-power curve after data cleaning and reconstruction

3.3 自原始数据输入各模型性能对比

本文提到的概率稀疏注意对Transformer 进行了改进，使其训练时长和精度都得到了有效提升，将编码器最终输出的特征图进行可视化处理如图8所示。颜色越接近黄色稀疏程度低，接近蓝色稀疏度高，Informer 的稀疏化的特征图相比Transformer，仅对少部分位置赋予更高权重，剩余的部分权重分布平均。

图8 编码器最终特征图输出可视化Fig.8 Visualization of final feature map output of encoder

采用2019 年3 月至2020 年2 月的国内某风电场气象数据和实测数据分别对四季的情况进行实验分析，数据集按照1：4 划分测试集和训练集。将过去1.5 h 的风速、风向、环境温度等共12 个变量作为输入，输出变量为15 min 的风电功率。该算例基于Python 实现。硬件采用CPU: AMD R-5800H，3.20 GHz，GPU: RTX 3070，8 GB，内存：16 GB 的计算机平台。

基于该数据集将本文提出的Informer 模型与自注意力模型Transformer、深度分解自回归模型Autoformer、重参数化自注意力模型Reformer 进行实验比对，使用拟合系数（R2），均方根误差（Root Mean Square Error，RMSE），EMA和平均训练时间t对各个模型的预测精度和时间进行评价。RMSE 的值用ERMS表示。ERMS用于衡量模型的绝对误差，值越小，绝对误差越小。R2表示预测功率和实际功率曲线拟合度，取值范围为（0，1），R2的值越接近1，说明拟合程度高，预测效果好。ERMS和R2的计算公式为:

式中：N为预测点数量；i为预测点序号；为预测值；yi为实测值；为平均值。

原始数据输入预测模型中，Informer 模型采用使用图形处理器GPU 来加速深度学习模型的训练。将尚未清洗重构的原始风电数据集，归一化后输入各个模型中。

从图9 可以看出，未经过数据修正的原始功率曲线具有显著的间歇性，在功率值接近0 的时间段内Autoformer，Reformer 的预测结果与实际功率曲线有着显著的差异，而本文的Informer 模型在各个时间段均的拟合结果表现最佳。

图9 原始数据输入各个模型性能对比（春季）Fig.9 Performance comparison of various models for raw data input（spring）

3.4 修正后的数据集输入各模型性能对比

将原始风电数据通过KCI 数据清洗和LightGBM 数据重构来给数据降低噪声，归一化处理后载入到各个模型中，实验结果如图10 所示，经过数据修正之后的功率曲线，降低了气象波动、设备异常等误差的影响，风电功率得到了一定的提升，各个模型的拟合程度均有所提升。

图10 修正数据输入各个模型性能对比（春季）Fig.10 Performance comparison of various models for corrected data input（spring）

表3 为四季实验结果。

表3 四季实验结果Table 3 Experimental results from four seasons

由表3 所示四季数据修正前后预测模型的实验结构或表明，与原始数据输入相比，该数据修正技术减低了预测误差，Informer 的ERMS，R2在数据修正前后都表现最佳。Autoformer 在数据修正后，ERMS，R2得到了明显的提升，说明Autoformer，Transformer 对数据噪声较为敏感。Reformer 具有一定的抗干扰能力，但是预测模型的性能表现不如Informer。

兼顾精度和更快的训练速度有助于电网调度决策，对于针对15 min 的风电功率短期预测，训练速度很重要。从表3 中可知，Autoformer 的训练时长最长，Informer 的训练时长最短。Informer 通过改进Transformer 概率稀疏自注意机制、蒸馏机制使得模型训练更高效，训练时长相比Transformer 有所下降。

综合上述，本文提出的数据修正的概率稀疏自注意短期预测相比传统的预测方法有一定的优势。

4 结论

本文提出了一种数据修正的概率稀疏自注意短期风电功率预测方法，采用集成异常检测KCI 方法对异常值进行检测，并利用LightGBM 对清洗后的数据进行学习，保留数据特征的同时对缺失数据集进行修复。本文提出的概率稀疏自注意在传统自注意力的基础上，用概率稀疏评估筛选出重要特征，相比于其他及基准算法，鲁棒性更强，具有良好精度的同时，提高了预测速度。本文采用西北某风电场实测数据进行方法有效性的验证，结论如下：

1）采用集成异常检测和LightGBM 缺失值修复，对比数据修正前后，4 个模型的精度都得到了提高。

2）从拟合系数、均方根误差、绝对误差、训练时长4 个方面来看，Informer 的模型效果最好，拟合系数可以达到94.5%，误差低于其他模型。

需要指出的是，该算法的执行复杂度取决于数据的长度和模型超参数，需要根据具体情况对超参数和输入数据长度进行调整。在实际工程中，受到各个不同风场具体的地理环境影响，实际分析会存在差异性；应注意使用合适的评价指标（如MAE、RMSE 等）来评估模型的预测效果，并根据实际需求对模型进行优化；需要考虑计算资源的限制。可以通过降低模型的复杂度、使用知识蒸馏等方法来降低计算复杂度，以满足实际应用的需求。