多视角剖析一道离心率质检题*
2023-11-10张桂腾
张桂腾
福建省莆田第十中学 (351146)
离心率是解析几何中的重要知识,近年高考及质检试题频频出现求解离心率的值或取值范围问题.这类问题常考常新,学生解决该问题有一定难度.一般求解策略为利用圆锥曲线的定义或几何特征寻找基本量间的关系,进而解决离心率问题.[1]本文从多个角度对2023年3月莆田市质检一道离心率问题剖析,探析求解离心率问题的一般策略.
一、试题呈现
二、解法探究
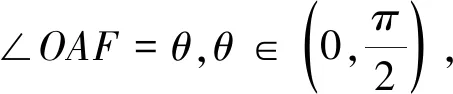
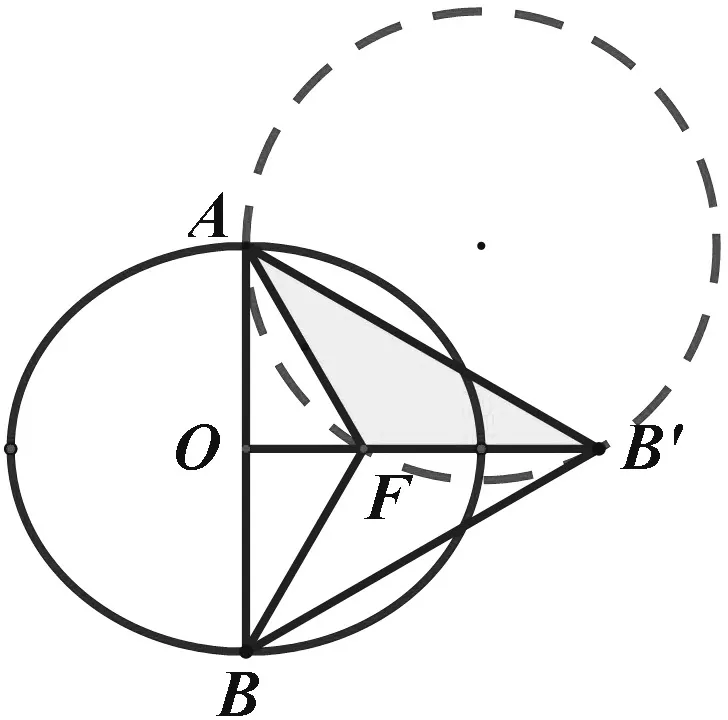
图1
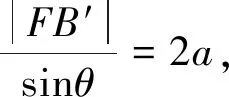
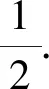

图2
评注:此解法根据直观想象得到过点A,B′,F的圆关于直线AF的对称圆的圆心恰为椭圆的左焦点,这是突破本题难点的关键.

图3

三、变式训练


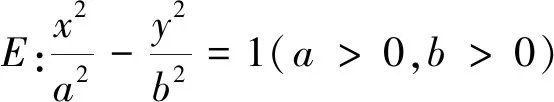
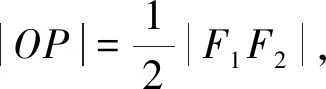
评注:一般地,与焦点三角形有关的计算常利用正弦定理、余弦定理、||PF1|-|PF2||=2a,得到a,c的关系.

解:如图4,设椭圆的左焦点为N,连接AF,AN,BF,BN,所以四边形AFBN为长方形,根据椭圆的定义|AF|+|AN|=2a,且∠ABF=α,则∠ANF=α,

图4




图5
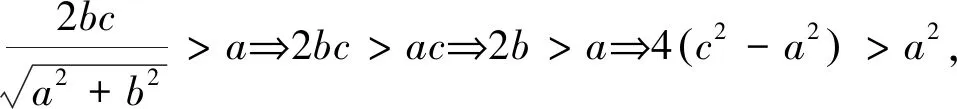
四、教学启示
求离心率的值(取值范围)需要构造一个含有F1,F2或数字的等式(不等式),往往综合性较强,是教学的一个难点.由以上例子中,教师可引导学生归纳以下方法:
1.从定义出发,特别注意第一定义中的焦点三角形问题,以椭圆为例,在焦点三角形中三条边中蕴含了F2的关系,因此如果能找出三条边的关系也就可以求出离心率的值;
2.分析已知条件中的几何特征,如题目中给出的等腰,中垂线,垂直等条件都可能是破解题目的入手点,由几何特征得基本量关系往往会简化运算;
3.求取值范围需建立一个含有|PF1|=ex0+a,|PF2|=ex0-a的不等关系,可有以下入手方向:从圆锥曲线本身所具有的不等关系入手;从直线和圆锥曲线的位置关系或点和圆锥曲线的位置关系入手;通过分析题目中的几何条件得出不等关系,例如出现的钝角锐角或者出现的三角形的形状,中垂线等.
