热值计量模式下川气东送管道运行优化研究

2023-11-09袁献忠

西南石油大学学报(自然科学版) 2023年5期

袁献忠

国家管网集团川气东送天然气管道有限公司，湖北武汉 430000

引言

天然气是一种优质、高效、低碳的化石能源。出于经济发展和环境保护的需求，全球天然气消费量持续增长，在世界能源结构中的地位不断上升。据预测，未来15 a 中国天然气市场仍将处于稳定增长阶段，2025 年中国天然气消费量将达到4 200×108m3，比2020 年净增1 000×108m3，2035年可达6 000×108m3以上[1]。天然气在到达用户之前，需要经历勘探、开发、生产、运输和存储等各个阶段。在运输阶段，大量天然气通过管道进行输送，这是因为天然气管道较其他运输方式而言，具有输气量大和输送效率高等优势。随着中国天然气管道的建设和发展，天然气管道的总里程不断增加，管道系统的结构也变得越来越复杂，这对管道系统的日常调度和运营管理提出了更加严峻的挑战。因此，利用现代优化技术，对天然气管道的运行调度进行合理优化，提升管道的输送效率和经济效益便显得迫切和重要。

目前，已有部分学者论述了中国在天然气管网运行优化领域的研究进展[2-4]。针对这个问题，相关的研究主要集中在优化目标、决策变量和求解方法等方面。根据研究问题中优化目标的不同，天然气管网的运行优化问题可以分为单目标优化和多目标优化。在单目标优化中，常见的优化目标有压气站能耗最小化[5-6]、管道经济效益最大化[7-8]及管道流量最大化[9]等。而在多目标优化研究上，学者们则主要考虑通过优化手段有效平衡不同目标之间的矛盾，实现管道整体运行状态的最优化[10-11]。

天然气管网运行优化问题的约束条件本身具有非线性，而压缩机开机数变量又具有离散性，因此，根据决策变量中是否包含压缩机开机数，又可以将优化模型分为非线性规划问题[12]和混合整数非线性规划问题[13-14]。针对优化问题的求解方法，又可分为传统的确定性算法[15-16]、现代随机优化算法[17-20]和商业求解器[21-22]。

天然气进行贸易结算依据的方式主要有体积计量和热值计量两种。相较欧美等国家而言，中国在天然气计量技术方面的研究起步较晚，除中国石油西气东输二线香港支线及中国海油崖城至香港海底管道供应香港中华电力公司，以及已经投产的广东和福建LNG 项目采用热值计量方式外，三大石油公司主要以体积计量方式进行天然气贸易计量，而热值计量方式由于使用范围广和相对精准，已成为现阶段国际通用的贸易计量方式[23-24]。

通过对中国天然气管网运行优化领域相关文献回顾发现，之前的学者大多以天然气体积计量为背景开展相关研究，极少有人考虑热值计量计价模式下的管网运行优化问题。然而，天然气的主要价值在于其燃烧产生的热量，为了保障不同品质天然气在交易平台上的公平竞争，促进国家级天然气交易中心的国际化发展，国家出台了《油气管网设施公平开放监管办法》。因此，研究热值计量计价模式下的天然气管网运行优化问题，探析该模式与传统体积计量模式下管网最优运行方案的差异，具有十分重要的价值和意义。

由于计量计价模式的转换对管网经济效益的影响巨大，本文选择以管网经济效益最大化为优化目标，以气源供气量、压缩机开机数和转速为决策变量建立相应的运行优化模型。该模型中还涉及节点压力、管道水力及压缩机运行等约束条件。在此基础之上，选择川气东送管道为优化实例，利用GAMS 建模系统和DICOPT 求解器进行优化求解。最后，对所获得的优化结果进行经济和技术分析。

1 天然气热值计量转换

目前，在涵盖管输天然气和液化天然气业务的国际天然气贸易中，普遍采用热值作为天然气的计量单位[25]。然而，中国现阶段仍采用体积计量为主，热值计量为辅的计价方式。该方式不利于天然气在交易时体现其本身的价值，影响到不同品质天然气在交易平台上的公平竞争。因此，在国家相关政策的引导下，大量学者对天然气热值计量问题进行了相关研究。部分学者论述了天然气实施热值计量的经济必然性和技术可行性[26-28]。此外，还有学者分析了中国计量现状和面临的问题，并提出了天然气热值计量计价的实施方案[29-30]。

通过对比分析各种价格转换实施方案，选取国家发布的天然气热值作为天然气价格转换方法的基准热值效果最佳。在该方案中，各用户利用国家发布的热值标杆，根据每次交易时天然气的实际热值来计算天然气交易价格。据此，提出了价格转换公式，如式（1）所示。该转换公式通过确定一个衡量单位体积天然气中所蕴含热量的基本数值（基准热值），将进行交易的天然气体积计量价格转换为热值计量价格。公式中的价格波动系数w 用于描述各用户交易时实际天然气的热值与国家发布的热值标杆之间的差异引起的价格波动。利用价格波动系数，可以使各用户在制定天然气热值计量价格时，更加符合实际交易时的天然气热值，提高天然气交易时价格制定的公平性。

式中：

SH—热值计量的价格，元/GJ；

SV—体积计量的价格，元/m3；

H0—天然气价格从体积计价转换为热值计价的基准热值，MJ/m3；

He—各用户接收的实际天然气热值，MJ/m3；

w—价格波动系数，无因次。

2 数学模型

为了便于数学模型的建立，基于有向图理论，本文将天然气管网系统简化为由节点和元件组成的系统，即G=(NNN,UUU)。图1 展示了简化后的典型天然气管网结构。系统中的节点用i表示，节点所在集合定义为NNN，i∈NNN。系统中的元件用e表示，元件所在集合定义为UUU，e∈UUU。节点集合NNN中又包含有注入节点子集，子集中元素用In表示；分输节点子集，子集中元素用Dn表示；连接节点子集，子集中元素用Tn表示。因此，节点集合NNN与各子集合关系为NNN=∪NNNDn∪。此外，元件集合UUU中包含有管道元件子集UUUpipe和压缩机站元件子集UUUcs，即UUU=UUUpipe∪UUUcs。管道元件子集UUUpipe中的元素用k表示，压缩机站元件子集UUUcs中的元素用j表示。基于以上定义，接下来将详细说明优化模型的系统假设、目标函数、约束条件和决策变量。

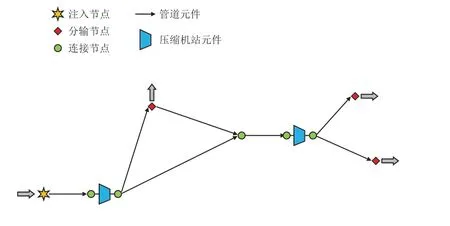
图1 典型天然气管网示意图Fig.1 Schematic diagram of typical natural gas pipeline network

2.1 系统假设

1）稳态流动假设

天然气在管道中流动通常处于不稳定状态（瞬态），在这样的状态下，天然气的水力、热力参数将随时间进行变化。但是，当研究输气管道系统年度或月度运行规划问题的时候，由于时间较长，系统不稳定性对研究结果影响较小，可忽略不计。因此，通常将长期天然气管道运行优化问题简化为稳态。

2）等温流动假设

通常情况下，天然气在沿管道流动过程中温度不断变化，并最终接近埋深处土壤温度。但是，实际应用表明，天然气温度变化值相对于开氏温度基准值（273.15 K）来说较小，在一定范围内变化对压力、流量影响不大。因此，假设天然气沿管道等温流动，温度设为293.15 K。

2.2 优化目标函数

管道运行效益最大化是管道运营商最为关注的重要目标。管道运行效益定义为天然气销售收入减去系统成本。系统成本又包括天然气购买成本和压缩机运行成本。管道运行效益最大化目标如式（3）所示

式中：

SH,Dn—分输节点处的天然气销售价格，元/GJ；

He,Dn—分输节点处天然气的实际热值，GJ/m3；

qDn—分输节点流量，m3/d；

SH,In—注入节点处的天然气购买价格，元/GJ；

He,In—注入节点处天然气的实际热值，GJ/m3；

qIn—注入节点流量，m3/d；

Ej—压缩机能耗价格，元/（kW·h）；

δj—压缩机开机数；

Wj—压缩机功率，kW；

tj—压缩机运行时间，h/d。

应用热值计量模式下的管道运行效益最大化相较体积计量模式下的管道运行效益最大化的区别在于购气成本与销售收入，体积计量的购气和售气成本使用体积单位结算，而热值计量下的购气与售气则是使用热值单位进行结算，使用热值进行结算能够充分体现市场的优质优价原则，能够满足终端用户的差异化需求，可以有效解决由于上游气质波动导致的结算争议。

2.3 等式约束条件

1）节点流量平衡

根据质量守恒定律，在任意节点处，流入节点的流量应等于流出节点流量。节点流量平衡约束如式（4）所示

式中：

qi—节点流量，m3/d，当天然气从节点流入管网系统，取值为正，当天然气从节点流出管网系统，取值为负；

βie—与第i个节点与第e个元件之间的连接关系系数，βie=0 时为第i个节点与第e个元件不相连接，βie=1 时为天然气从第e个元件流入第i个节点，βie=−1 时为天然气从第i个节点流出到第e个元件；

Qe—元件流量，m3/d。

2）管道流动方程

当天然气在管道中流动时，由于管道内壁存在一定的粗糙度，部分能量将损失。这将导致天然气的压力沿管道逐渐降低。管道流动方程由一维动量守恒方程推导而来，该方程可以很好地计算管道的压降情况。因此，可以利用该方程来表征管道的入口压力和出口压力之间的关系。

输气管道水力计算公式如式（5）、式（6）所示

式中：

Mk—管道质量流量，kg/s；

pa,k—管道入口压力，Pa；

∆hk—管道起终点高程差，m；

pb,k—管道出口压力，Pa；

“地是黄金板，人勤地不懒。”“地是宝，越种越好。”“一寸土地一斤粮，多种就能多打粮。”“人靠地长，地靠人长。”说明土地的重要性。

Dk—管道内径，m；

λk—管道摩阻系数，无因次；

Zk—天然气压缩因子，无因次；

R—天然气气体常数，R=8.314 J/(mol·K)；

T—管道平均温度，K；

Lk—管道长度，m；

g—重力加速度，g=9.8 m/s2。

3）摩阻系数

摩阻系数λk是气体流动计算的重要参数之一，它与天然气流态和管道的粗糙程度等因素有关。在众多公式中，Colebrook 公式被普遍使用，且计算精确度高。Colebrook 公式由普朗特水力光滑管公式和尼古拉兹完全粗糙管公式推导得到，如式（7）所示

式中：

εk—管道内壁绝对当量粗糙度，m；

Rek—雷诺数。

4）压缩因子

压缩因子表示实际气体受到压缩后与理想气体受到同样的压力压缩后在体积上的偏差，是气体流动时必须考虑的一个校正因子。BWRS 方程是公认的计算精度较高的经验方程，适用性广泛。BWRS方程通过修正BWR 方程而得到，方程具有11 个轻烃组分系数，每个系数可通过相关的计算公式和计算规则得到。该方程如式（8）所示

式中：ρk—管道中天然气密度，kmol/m3；

A1∼A11—方程的11 个系数，每个系数均可通过相关的计算公式和规则得到。

5）压缩机方程

压缩机是天然气输气管道系统中最复杂的设备。压缩机特性曲线指压缩机压头、等熵压缩效率、进气流量和转速之间的关系曲线。图2a 展示了压缩机压头、进气流量和转速之间的关系曲线。图2b展示了等熵压缩效率与进气流量和转速的关系曲线。通过压缩机特性曲线能够描述出压缩机的运行规律，并估算出其运行参数。

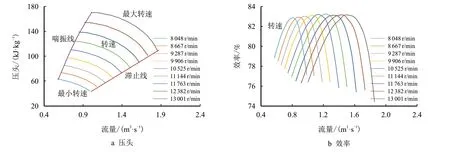
图2 压缩机特性曲线Fig.2 Compressor characteristic curve

然而，在建模过程中，需要用数学语言来描述压缩机特性曲线。因此，压缩机特性曲线常常被拟合成多项式方程，这样的方程称为压缩机特性方程。根据压缩机特性曲线所拟合出的压头特性方程和效率特性方程分别如式（9）和式（10）所示

式中：

Hj—压缩机压头，kJ/kg；

ωj—压缩机转速，r/min；

—压缩机进气流量，m3/s；

AH，BH，CH，DH—压缩机压头特性方程拟合系数；

Ae，Be，Ce，De—压缩机效率特性方程拟合系数。

在压缩机工作过程中，当进气流量过低，将出现喘振现象；而进气流量过高，又将出现滞止现象。这两种工况的出现都将影响压缩机的正常运作，甚至可能会造成设备损坏。因此，需要对进气流量进行限制，将压缩机控制在一定范围内工作。压缩机喘振线和滞止线分别位于图2a 的左右两侧。通过将喘振线和滞止线拟合成多项式方程式（11）和式（12），可以得到进气流量的限制范围。进气流量限制如式（13）所示

式中：

Asu，Bsu，Csu，Dsu—压缩机喘振方程拟合系数；

Ast，Bst，Cst，Dst—压缩机滞止方程拟合系数。

通过压缩机特性方程计算出压头后，便可计算压缩机的排气压力

式中：

—压缩机进气端的天然气压缩因子；

—天然气绝热指数；

—压缩机进气压力，MPa；

—压缩机排气压力，MPa。

最后，根据压缩机压头和天然气质量流量，还可以计算出压缩机功率

式中：

mj—压缩机质量流量，kg/s；

2.4 不等式约束条件

1）节点流量约束

天然气作为一种化石能源，进入长输管道的流量要受到气源在一定时间内的最大产量或最大处理能力的限制。此外，对于不同区域和不同类型的天然气用户，有不同的消费需求量。因此，在每个节点，节点流量应满足最大或最小流量约束

式中：

qi,min—最小节点流量，m3/d；

qi,max—最大节点流量，m3/d。

2）节点压力约束

同样的，气源或用户因自身能力或需求，对管道中各节点的压力也有一定要求。管道中各节点的压力也需满足最大或最小压力约束

式中：

pi,min—最小节点压力，MPa；

pi,max—最大节点压力，MPa。

3）压缩机转速约束

压缩机转速与设备性能相关，并存在最大和最小转速限制。该约束如式（18）所示

式中：

ωj,min—压缩机最小转速，r/min；

ωj,max—压缩机最大转速，r/min。

4）压缩机功率约束

压缩机站内的单台压缩机设备存在最大和最小轴功率约束，该约束如式（19）所示

式中：

Wj,min—压缩机最小功率，kW；

Wj,max—压缩机最大功率，kW。

2.5 决策变量

根据前述的目标函数和约束条件，本优化模型的优化变量分别是：注入节点流量、各压缩机站中压缩机开机数和转速。其中，注入节点流量和压缩机转速为连续变量，压缩机开机数为离散变量。又由于约束条件具有非线性，因此，本文所建立的优化模型属于混合整数非线性规划模型，求解具有一定难度。

3 求解方法

求解过程采用通用数学建模系统（GAMS）进行编程求解。GAMS 可以用于求解线性规划问题、非线性规划问题、混合整数线性规划或混合整数非线性规划问题。GAMS 将算法封装于系统内部，能够实现将复杂数学模型用简洁高效的编程语言进行描述。用户描述好数学模型后，系统将自动调用算法进行求解，从而使得求解过程更加简便且高效。

本文所建立的天然气管网运行优化模型求解属于MINLP 问题，模型在GAMS software version 24.8.2 上进行建模，并调用系统自带的DICOPT 求解器工具对数学模型进行求解。DICOPT 求解器基于广义简约梯度法和分支定界法获得最优解。运行平台为Intel(R) Pentium(R) CPU G4560 3.50 GHz 的处理器和8 GB 的运行内存（RAM）。

4 分析与应用

4.1 算例研究

本文选择中国的川气东送管道作为研究算例。该管道总长为2 229 km，含有1 条干线、1 条专线、4 条支线、2 个注入节点、29 个分输节点和7 座压缩机站。输气管道的结构如图3 所示。管道的设计运行压力为10 MPa，干线管道内径为995 mm，管道壁厚为21 mm，管道内壁绝对当量粗糙度为0.01 mm。管道中两个气源的天然气组分如表1所示。

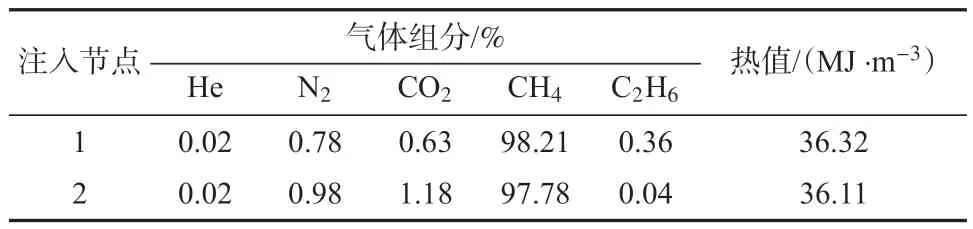
表1 各注入节点天然气组分和热值Tab.1 Natural gas components and calorific value of each injection node

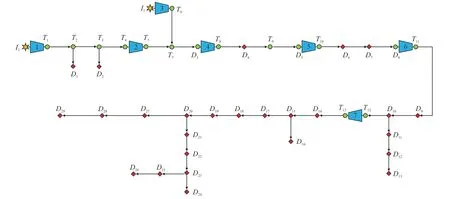
图3 大型天然气输气管道结构图Fig.3 Structure of large natural gas transmission pipeline

以该管道在2020 年9 月某日的现场实际运行工况为例开展研究。当日管道总输量为4 146.12×104m3，管道中各节点的流量分配情况如表2 和图4所示。在注入节点1 处，恒定流量为2 295.67×104m3/d 的天然气以7.45 MPa 的压力注入管道，而在注入节点2 处，有1 850.45×104m3/d天然气以4 MPa 的压力注入管道。下游分输节点较多，大部分分输节点需求流量较小，维持在200×104m3/d 左右，其中，需求流量超过400×104m3/d 的分输节点共有4 处，分别为分输节点2、16、22 和28。对于下游各节点的压力约束，主要有分输节点26 压力要大于4.8 MPa，分输节点29 压力要大于5.0 MPa。

表2 各注入节点供气量Tab.2 Air supply at each injection node

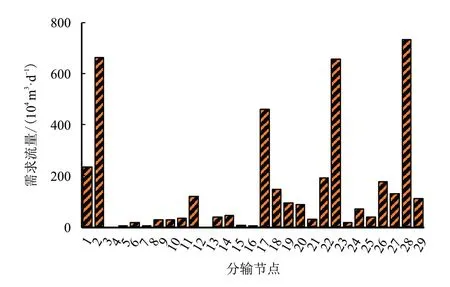
图4 各分输节点需求流量Fig.4 Demand traffic of each node

根据2020 年企业长输管道采购价格表确定注入节点出厂价格；并根据2019 年发布的关于调整天然气基准门站价格的通知—发改价格[2019]562号，确定了体积计量模式下的各分输节点天然气基准门站价格。选取2018 年前的国家一类气标准36.00 MJ/m3作为基准热值，通过式（1）可计算出热值计量模式下各分输节点的天然气购买价格，如图5所示。

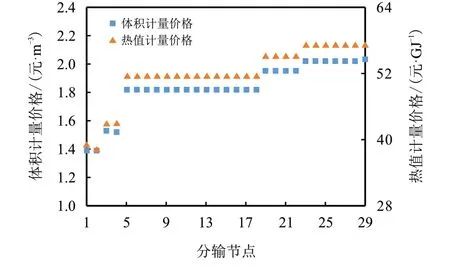
图5 体积计量与热值计量模式下的购气价格Fig.5 Purchase gas price under volume measurement and energy measurement mode

7 座压缩机站中，各站站内配置的压缩机型号相同，单台压缩机最大功率分为7 200、11 000和15 000 kW 共3 个等级，所有压缩机均由电动机驱动。表3 展示了各压缩机站的配置参数。不同的压缩机站在不同的时间建设完成，并且具有不同的增压能力。因此，压缩机站的压缩机特性也各不相同。此外，根据管网运行公司在2020 年发布的产品运行报告计算压缩机运行费用系数为0.56 元/（kW·h）。

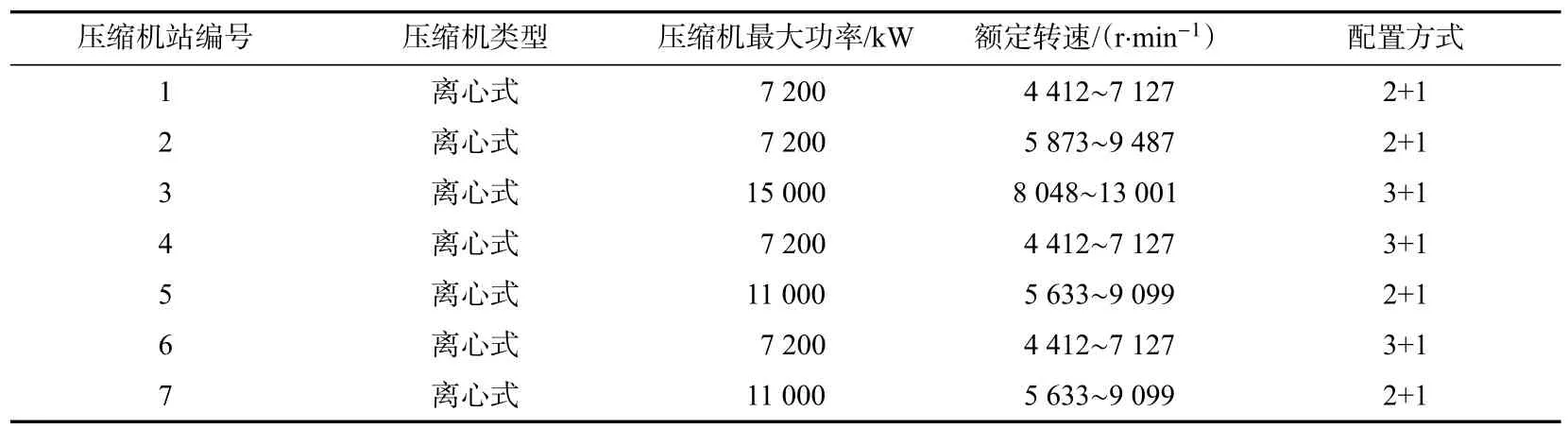
表3 压缩机站配置参数Tab.3 Compressor station configuration parameters

将压缩机厂家提供的压缩机性能参数进行分析计算，使用最小二乘法对压缩机性能参数进行拟合，得到各压缩机特性方程拟合系数，如表4 和表5 所示。

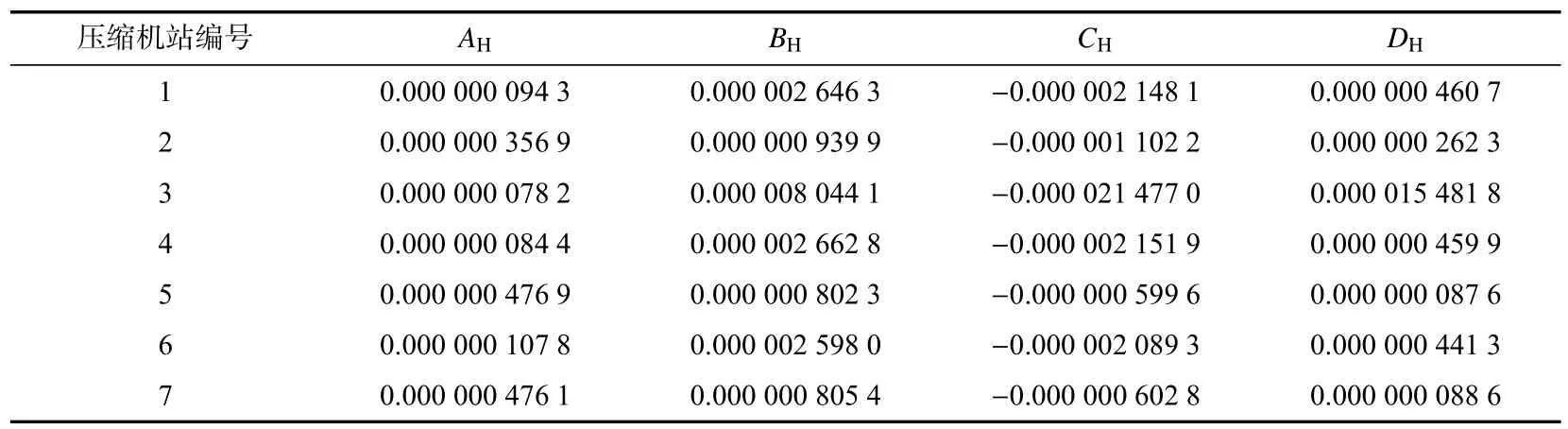
表4 不同压缩机站的压头特性方程拟合系数Tab.4 Head characteristic equation coefficients of different CSs

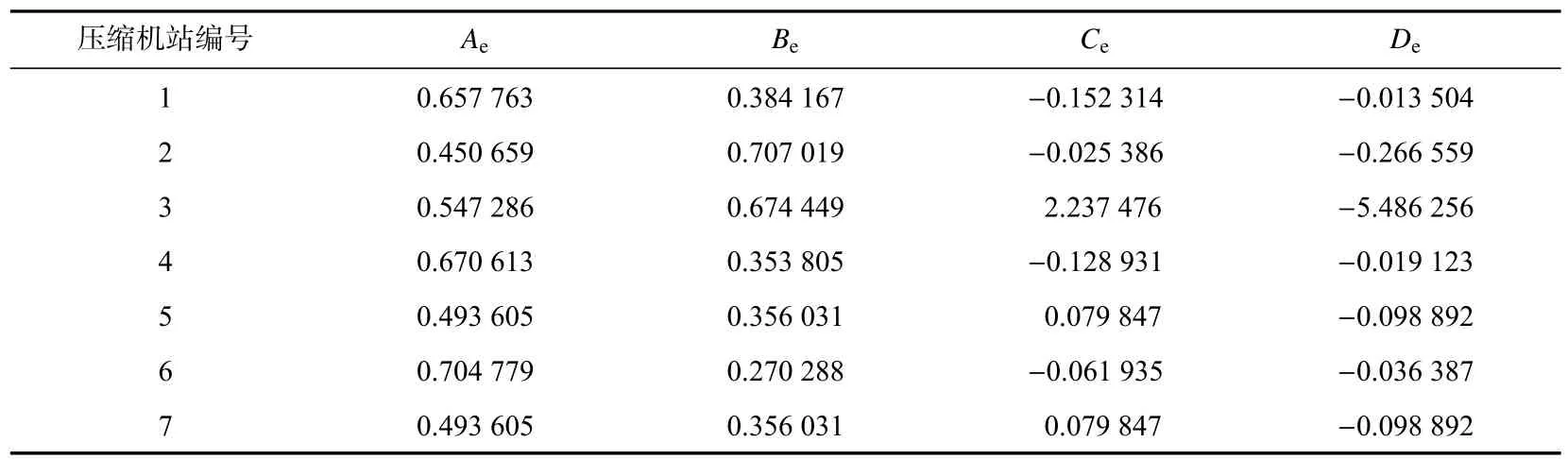
表5 不同压缩机站的效率特性方程拟合系数Tab.5 Efficiency characteristic equation coefficients of different CSs

4.2 分析与讨论

将所建立的优化模型应用于川气东送管道，采用GAMS 建模系统和DICOPT 求解器对优化问题进行求解，并对所获得的优化结果进行分析。为了充分说明热值计量模式下管道运行方案与传统的体积计量模式下管道运行方案的差异，选择了该管道在当前体积计量模式下的一套现场方案为依据，进行对比分析，如表6 所示。

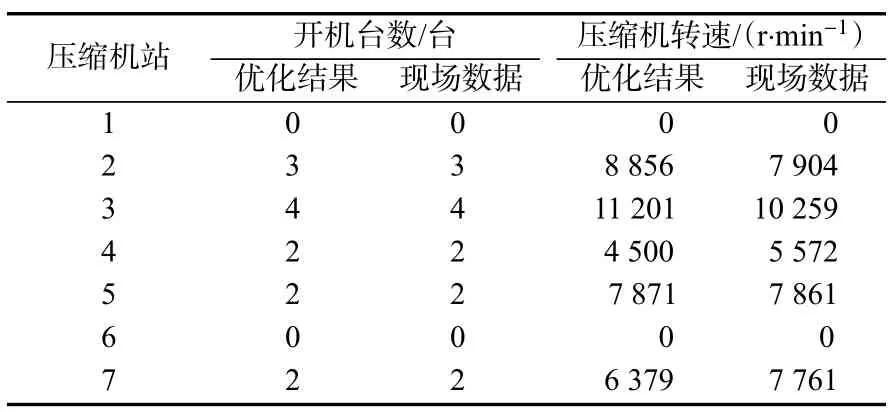
表6 优化结果与现场实际运行方案对比Tab.6 Comparison between optimization results and actual operation schemes on site

热值计量下优化方案和体积计量下现场方案的费用对比情况如表7 所示。通过表7 可以看出，热值计量下的优化方案比体积计量下的现场方案多盈利202.838 万元，利润提高了近10.82%。此外，热值计量下管道售气收入提高了235.449 万元，压缩机站运行能耗费用降低了4.281 万元。虽然购气成本略有增加，但其增加的幅度远低于售气收入增加的幅度。总体来看，与体积计量下现场方案相比，热值计量下优化方案为天然气企业带来更多的利润。

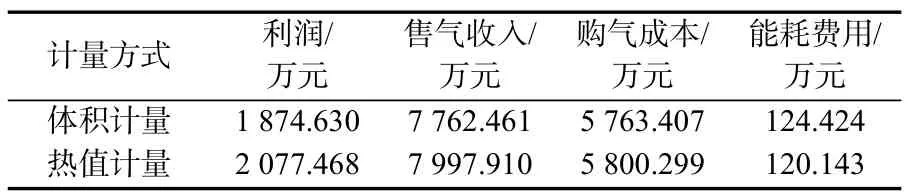
表7 热值计量下优化方案和体积计量下现场方案的费用对比Tab.7 Cost comparison of optimization scheme under calorific value measurement and field scheme under volume measurement

由图6 可知，优化方案改变了各注入节点的供气量。在实施热值计量方式改革后，热值计量价格通过原有的体积计量价格转换获得，因此，在注入节点处的购气价格与其自身的热值有关，注入节点处气体所含热值越高，确定的能量计量单价越高。所以，为扩大售气收益，需在满足管网输送要求的前提下，尽可能选择价格低的注入节点供气。在优化方案中，由于注入节点2 的天然气能量计量价格较注入节点1 低，所以注入节点2 提供了更多的流量，增加了33.8 m3/s，注入节点1 供应的流量相应减少。

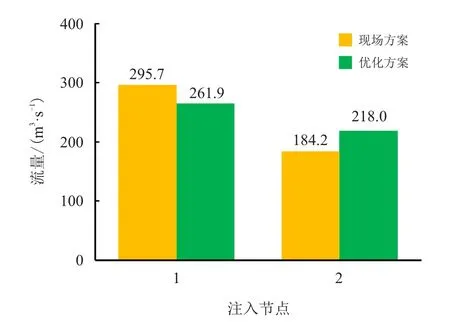
图6 热值计量下优化方案和体积计量下现场方案的注入节点流量对比Fig.6 Comparison of injection node flow between the optimization scheme under calorific value metering and the field scheme under volume metering

由图7 可知，由于不同方案中各注入节点供应流量的改变，使全线的增压方式产生一定的改变。现场方案和优化方案均在压缩机站2 处产生最高压力，分别为9.61 MPa 和9.85 MPa，此处优化方案达到了设置的管道运行压力上限。在压缩机站7 处，两种方案的出站压力均为8.95 MPa，管道末端分输节点29 压力均为5.38 MPa，验证了数学模型的准确性。同时，整体可以看出，优化方案与现场的运行方案差别不大，说明模型优化求解结果良好。

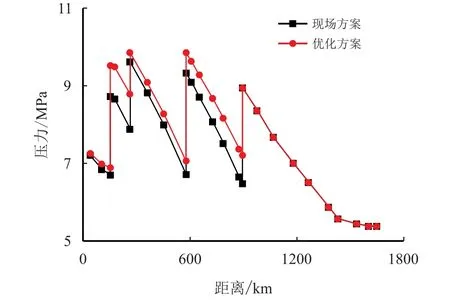
图7 热值计量下优化方案和体积计量下现场方案的管线压力对比Fig.7 Comparison of pipeline pressure between optimization scheme under calorific value measurement and field scheme under volume measurement

在两套方案下，全线各站的压缩机开机方案完全一致。其中，压缩机站2 开机3 台、压缩机站3 开机4 台、压缩机站4 开机2 台、压缩机站5 开机2台、压缩机站7 开机2 台，压缩机站1 和压缩机站6 未投入运行。图8 展示了热值计量下优化方案和体积计量下现场方案的压缩机转速对比。从图8 可以看出，优化方案主要在输气管道干线前段进行增压，在压缩机站2 处和压缩机站3 处的压缩机转速较高，也相应产生了较高的能耗费用，而在压缩机站4 处和压缩机站7 处的压缩机转速较低，能耗费用也较低。对比分析现场方案采取的增压方式，可知现场方案中各站点运行的压缩机转速普遍偏低，各站点增压量较为均匀，但这也产生了较高的压缩机运行费用。

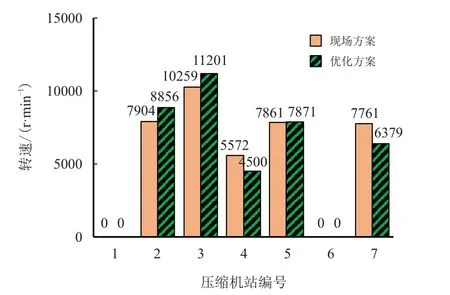
图8 热值计量下优化方案和体积计量下现场方案的压缩机转速对比Fig.8 Compressor speed comparison between the optimization scheme under calorific value measurement and the field scheme under volume measurement