高阶多自主体系统的H∞时变编队跟踪控制
2023-11-09寇元哲韩娜妮
寇元哲, 韩娜妮
(陇东学院 电气工程学院,甘肃 庆阳 745000)
编队控制是多自主体系统协调控制的一个重要研究方向,由于其在军事、民用等领域中的广泛应用[1-3],受到了大量学者的关注.
在时变编队跟踪控制中,要求follower自主体形成并保持所期望的时变编队,并且跟踪预期的轨迹.文献[4-5]研究了二阶多自主体系统的时变编队跟踪控制问题.文献[6]针对高阶切换多自主体网络,设计了时变编队控制协议,并且详细分析了编队参考函数.进一步,文献[7]考虑了多leader自主体的情况.文献[8]针对UAVs(unmanned aerial vehicles)组成的有向切换多自主体网络,利用局部邻接信息设计了时变编队跟踪控制协议,并且提出了实现控制目标的算法.文献[9]基于事件触发机制和自适应控制方法,研究了高阶多自主体系统的时变编队跟踪控制.文献[10-13]是针对异构多自主体系统的时变编队跟踪控制成果.在文献[10]中,假设leader输入未知,利用自适应更新机制设计了编队跟踪控制协议.考虑系统中存在多个模型不同的leader自主体,为克服假设条件的限制,文献[11]利用分布式观测器方法研究了时变编队跟踪问题.Duan等[13]通过构造有限时间自适应观测器估计leader的状态和矩阵,以实现系统的有限时间时变输出编队跟踪控制目标.文献[14-15]是非线性系统的时变编队跟踪控制研究成果.
在实际运行环境中,系统不可避免受到外界干扰的影响,H∞分析方法常用于研究多自主体系统的一致性问题.文献[16-17]研究了多自主体系统的H∞一致性问题.文献[18]是异构多自主体系统存在时延时H∞输出反馈控制研究成果.目前,已有考虑外界干扰的时变编队跟踪控制研究成果.当二阶多自主体系统中存在干扰时,文献[19]通过状态观测器对干扰补偿进行估计,设计了鲁棒时变编队跟踪控制协议.文献[20]考虑了二阶多自主体系统存在执行器故障时的时变编队跟踪问题.文献[21-22]分别通过自适应更新机制和设计干扰观测器研究了高阶多自主体系统的时变编队跟踪问题.文献[23]研究了鲁棒H∞保性能时变编队跟踪控制问题.
在高阶多自主体系统时变编队跟踪控制研究成果中,文献[7-9]没有考虑外界干扰及时变时延的影响,并且文献[8-9]假设系统中只有一个leader自主体.文献[21-23]考虑了外界干扰对系统实现时变编队跟踪控制的影响,但都假设系统中只有一个leader自主体.相对于一个leader自主体,多leader自主体系统具有更广泛的适用性.基于以上研究成果,本文考虑时变时延和外界干扰,研究存在多个leader的高阶多自主体系统的H∞时变编队跟踪控制.首先,基于邻接信息,设计了分布式时变编队跟踪控制协议.然后,利用Lyapunov-Krasovskii函数分析了协议有效的充分条件.本文的主要创新点是研究了存在时延和外界干扰的多leader自主体系统的时变编队跟踪控制问题.
1 系统描述
假设多自主体系统由N个自主体构成,其中M个follower自主体,N-M个leader自主体.Follower自主体的数学模型描述为
(1)
其中:xi(t)∈Rn,ui(t)∈Rr,yi(t)∈Rm分别是第i个自主体的状态、输入及输出向量,ωi(t)∈L2[0,∞)是有界外界干扰,A,B,C,B1为已知适维常数矩阵.
N-M个leader自主体的动态模型为
(2)
其中:xj(t)∈Rn,yj(t)∈Rm为第j个leader自主体的状态和输出向量.

定义1若follower自主体能接收到所有leader自主体的信息,则称为well-informed自主体.若follower自主体不能接收到任一leader的信息,则称为uninformed自主体.
假设1系统中的follower自主体为well-informed自主体或uninformed自主体,并且对于每个uninformed自主体,至少存在一个well-informed自主体与其之间存在有向路径.
当假设1成立时,多自主体系统(1)~(2)的Laplacian矩阵可表示为
(3)
其中:L1∈RM×M,L2∈RM×(N-M).bj表示第j个leader自主体的信息权值,bj=1或bj=0.



(4)
则follower自主体实现了时变编队跟踪控制,其中hi(t)为第i个follower自主体的时变编队函数.
2 H∞时变编队跟踪控制
针对follower自主体,设计时变编队跟踪控制协议:
xl(t-τ(t))+hl(t-τ(t)))+
xj(t-τ(t))),i=1,2,…,M,
(5)
其中:K∈Rm×n是待定常数矩阵;τ(t)是时变时延,满足
(6)

令
将协议(5)代入系统(1)可得
(L2⊗BK)xE(t-τ(t))+(IM⊗B1)ωF(t)-
(L1⊗BK)hF(t-τ(t)),
(7)
其中:IM是M维单位阵,⊗表示Kronecker积.
Leader自主体可以写为
(8)
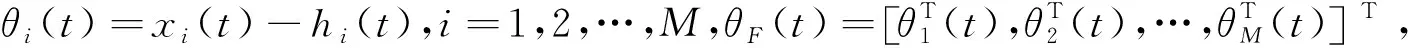
(L2⊗BK)xE(t-τ(t))+(IM⊗A)hF(t)-
(9)
令
则
φF(t)=(L1⊗In)θF(t)+(L2⊗In)xE(t),(10)
并且
(L1⊗B1)ωF(t).
(11)
为方便分析H∞时变编队跟踪,引入下列引理.
引理2[26]对于向量c(t)∈Rn,d(t)∈Rn和矩阵Z∈Rn×n,下式成立:
±2cT(t)d(t)≤cT(t)Zc(t)+dT(t)Z-1d(t).
(12)
引理3[27]假设ζ(t)∈Rn是一阶连续微分向量函数,则对于任意矩阵M1∈Rn,M2∈Rn和S=ST>0,下式成立:
(13)

Φ0+Re(λi)Φ1+Im(λi)Φ2<0,i=1,2,…,M.
定理1当假设1成立时,对于给定的H∞控制性能指标参数γ,若下列条件同时满足:
(14)
(ⅱ) 存在正定对称矩阵R、Q、S和矩阵M1、Μ2满足
(15)
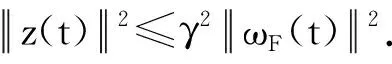
z(t)=(IM⊗C)φF(t),


(16)
(17)
系统(17)的稳定性等价于下列系统的稳定性:
(18)
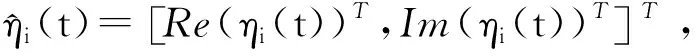
(19)
其中:
ΛA=diag{A,A},ΛB=diag{B,B},ΛK=diag{K,K},
为分析系统(19)的稳定性,设计Lyapunov-Krasovskii函数:
Vi(t)=Vi1(t)+Vi2(t)+Vi3(t),i=1,2,…,M,
(20)
其中:
根据引理2,对 (20) 式求导可得
(21)
其中:δ1为正常数,
(22)
(23)
根据引理3可得
(24)
定义
zi(t)=Cφi(t),i=1,2,…,M,
则
(25)
即
(26)

(27)
即
(28)
定义
(29)

(30)
其中:
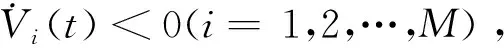

当控制协议增益矩阵K未知时,可通过以下定理求解矩阵K.
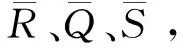
i=1,2,3,4,
(31)


根据Schur’s补原理,(15)式可写为
i=1,2,3,4,
(32)

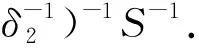
(33)

3 数据仿真
考虑由4个follower自主体和2个leader自主体组成的多自主体网络,其网络拓扑见图1,满足假设1.
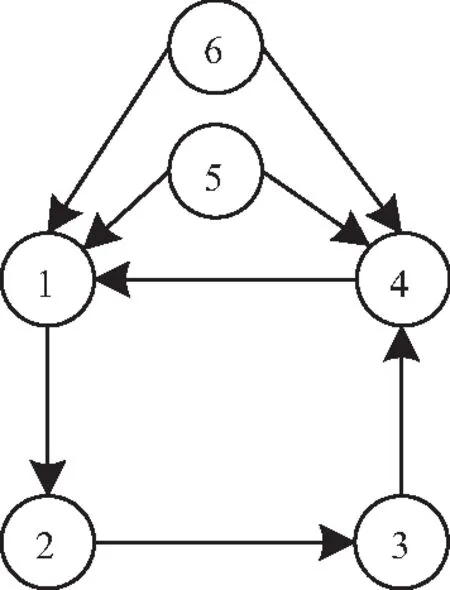
图1 多自主体系统网络拓扑
为实现时变编队跟踪控制,假设时变编队函数为
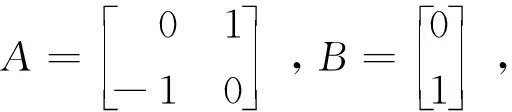
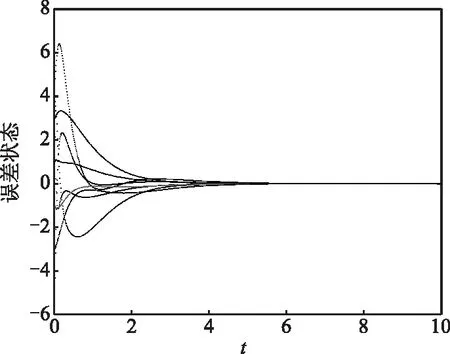
图2 误差系统(11)状态曲线
为进一步验证时变编队跟踪控制协议的有效性,将协议(5)用于follower自主体(1),可得follower自主体在t=3 s,6 s,10 s,15 s的状态轨迹(图3).在图3中,在时变时延和有界外界干扰的影响下,4个follower自主体在控制协议(5)的作用下最终形成所要求的时变编队.

图3 follower自主体状态
图4为follower自主体的编队跟踪轨迹图,4个follower自主体形成所要求的时变编队,并且跟踪leader自主体状态的凸组合.

图4 follower自主体时变编队跟踪轨迹
4 结语
本文针对存在多个leader的多自主体系统,考虑时变时延及外界干扰对系统的影响,研究了连续多自主体系统的时变编队跟踪控制问题.针对设计的时变编队跟踪控制协议,分析了协议有效的充分条件,并且给出了协议增益矩阵的具体形式.后续的研究方向主要是异构多自主体系统的时变编队跟踪问题.
