冷弯薄壁型钢槽形截面压弯构件的滞回性能有限元分析

姚行友, 杨嘉宝 , 胡成立, 刘亚菲, 余黎鹏, 戴荣凯

(1.南昌工程学院 土木与建筑工程学院,江西 南昌 330099; 2.南昌工程学院 江西省水利土木工程基础设施安全重点实验室,江西 南昌 330099; 3.江西省地质调查勘查院 矿产勘查所,江西 南昌 330099)

为实现碳中和目标,国家大力推动钢结构建筑发展,从而加快传统建筑行业的转型升级的步伐.装配式冷弯薄壁型钢结构凭借高度集成化、产业化和绿色经济等优势快速发展[1—3].我国是地震多发国家,为推动低、多层冷弯薄壁型钢房屋在我国的发展,针对抗震设防区的冷弯薄壁型钢房屋的抗震性能研究至关重要.王士奇等通过ABAQUS对冷弯薄壁槽形截面轴压构件和压弯构件在循环荷载作用下的滞回性能进行分析[4—6],结果表明,构件受局部屈曲应力的影响,滞回性能过早退化,而通过在构件上设置卷边或中间加劲可改善这一性能.孟庆铜等通过ANSYS对矩形截面冷弯薄壁型钢在常轴力、循环弯矩作用下的滞回性能进行分析[7],结果表明,初始缺陷对构件的局部屈曲应力影响较大,构件的滞回性能主要受轴压比、宽厚比、长细比的影响.杨娜等通过实验和有限元软件对冷弯薄壁C型钢压弯构件的滞回性能进行研究[8],并提出格构机理模型.基于该模型的分析结果表明,轴压比和宽厚比对构件的滞回性能影响较大.该实验也给出压弯构件的恢复力模型.冷弯薄壁C型钢轴压构件和受弯构件的滞回性能实验结果表明[9—10],屈曲模式是影响构件承载力降低、刚度退化、能量耗散的关键因素.目前,针对冷弯薄壁型钢构件在往复荷载作用下的滞回性能研究还不够完善.笔者通过ABAQUS建立冷弯薄壁型钢槽形截面压弯构件的滞回模型,分析构件的长细比、宽厚比、轴压比和材料屈服强度等对构件的延性系数、能量耗散和刚度退化规律等的影响,为该类构件在循环荷载作用下的滞回性能研究提供参考.

1 有限元模型的建立与验证

1.1 有限元模型的建立

冷弯薄壁型钢槽形截面压弯构件的有限元模型见图1,采用九节点减缩积分薄壳单元S9R5,考虑材料和几何双重非线性因素[11].构件下端完全固结,上端将约束点耦合在槽形截面的形心处,上端z方向施加恒定竖向荷载N,y方向施加反复水平推、拉位移.整体屈曲缺陷取构件长度的L/750,局部缺陷的初始缺陷取构件的一阶屈曲模态[12].

图1 有限元模型

冷弯薄壁型钢槽形截面压弯构件采用理想弹塑性模型.模型壳单元材料的属性:弹性模量E=2.06×105MPa,泊松比μ=0.3,屈服强度fy=345 MPa,抗拉强度fu=450 MPa.有限元模型加载制度见图2[13].由于冷弯薄壁型钢在屈曲失稳后变形较大,承载力下降速度较快.为了分析屈曲和极限荷载下的全过程,在构件上端施加水平往复位移,加载控制分弹性、屈曲2个阶段,弹性阶段每级位移循环1圈,每级为±0.25δy,±0.50δy,±0.75δy;屈曲后每级循环3圈,每级为±1.0δy,±1.5δy,±2.0δy,±2.5δy,±3δy,…加载直至构件破坏或发生严重变形.

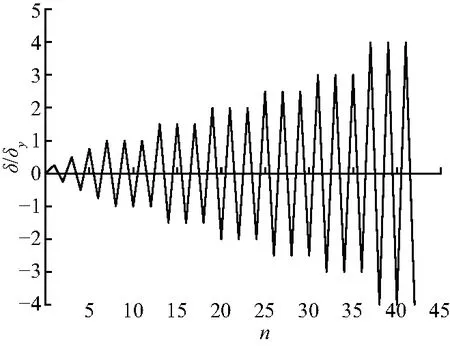
图2 加载制度

屈服位移δy的计算公式:

(1)

式中:n为构件的轴压比;σy为材料的屈服强度;E为构件的弹性模量.

1.2 有限元模型的准确性验证

通过建立的有限元模型对文献[13]中的试件C1-BC-L30-70-02和C2-BC-L60-35-02进行分析,试件的实际尺寸见表1,屈服强度分别为291.0,270.3 MPa.通过有限元分析得到构件的滞回曲线和破坏模式(图3～图4).

表1 试件的参数

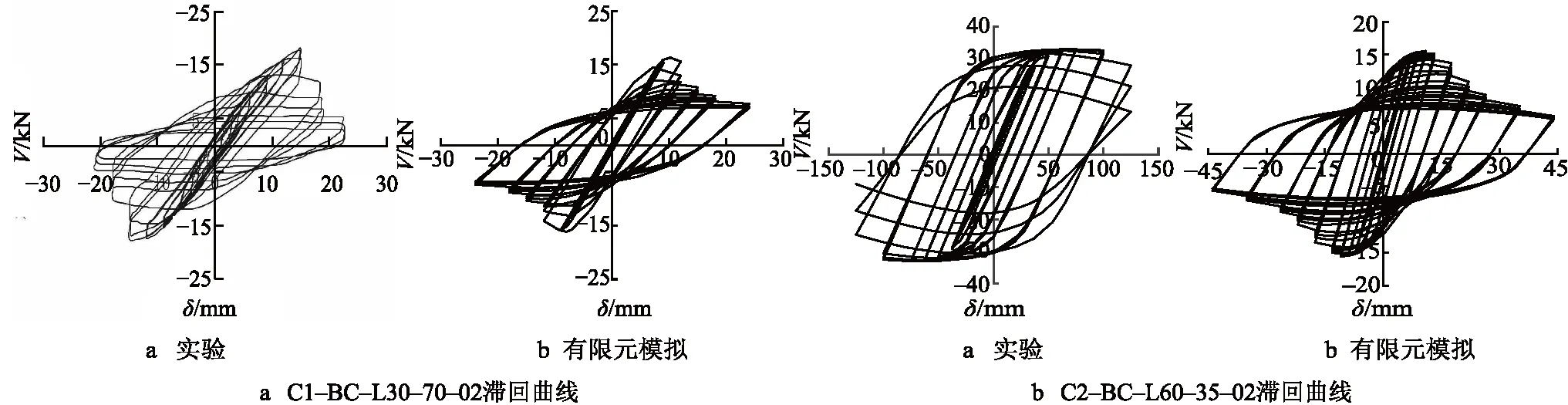
图3 滞回曲线对比

图4 破坏模式比较

由图3可知,有限元分析所得的滞回曲线与实验所得的滞回曲线,在最大承载力和刚度退化等方面比较一致.由图4可知,有限元分析所得的破坏形态与实验所得的构件后期破坏变形基本一致.C1-BC-L30-70-02的破坏为柱脚处发生腹板的局部鼓起、翼缘内聚;C2-BC-L60-35-02的破坏为柱脚处腹板内凹、翼缘处轻微外扩.因此文中采用的有限元分析模型是合理、可行的.

2 冷弯薄壁型钢压弯构件的设计

在用有限元模型进行滞回性能分析中,把冷弯薄壁型钢槽形截面压弯构件设计成4种长细比、4种宽厚比、5种轴压比和3种屈服强度的构件(表2).构件编号规则见图5.例如,编号为C5-BC-L50-50-03-Q2的构件:BC表示加载方式为压弯滞回加载;L50表示构件的长细比为50;50表示腹板与厚度的比为50;03表示对构件施加0.3倍的轴压比荷载;Q2表示钢材等级为Q235(Q3表示Q390,其他均为Q345).

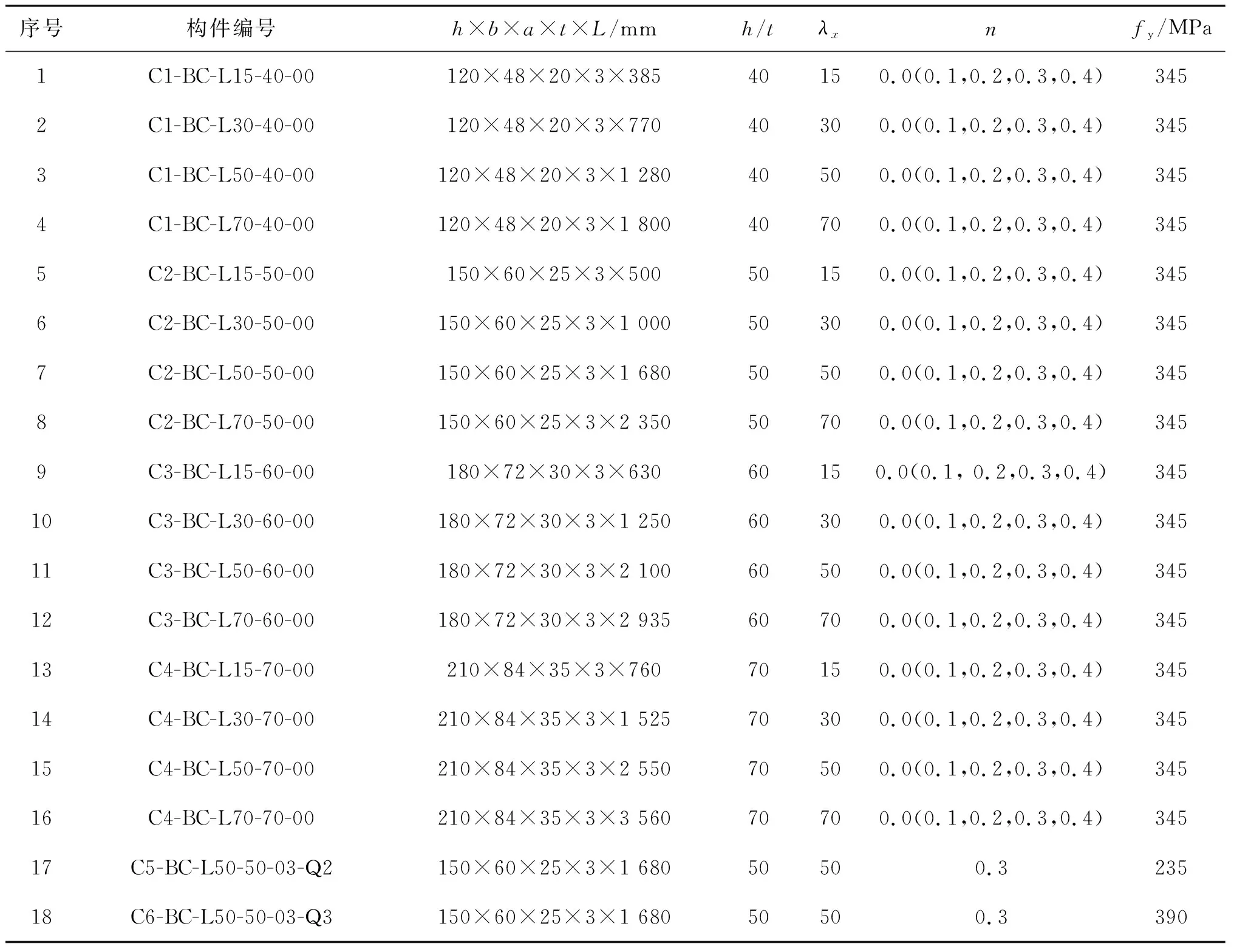
表2 冷弯薄壁型钢槽形截面压弯构件滞回性能分析中的参数

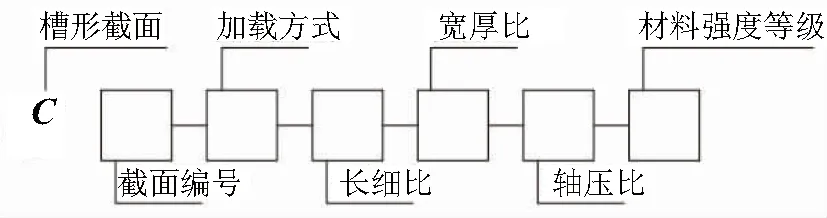
图5 构件编号规则

3 冷弯薄壁型钢槽形压弯构件的滞回特性

通过有限元模型对不同长细比、宽厚比、轴压比和材料屈服强度的82根冷弯薄壁型钢槽形截面压弯构件的滞回曲线和骨架曲线进行分析,考察各参数对构件的承载力、延性系数、耗能能力及刚度退化规律的影响[14].限于篇幅,后续仅对部分构件结果进行分析.

3.1 破坏模式

通过有限元模型得到压弯构件C1-BC-L30-40-02,C3-BC-L30-60-03,C3-BC-L70-60-02的破坏模式(图6),它们分别发生局部屈曲、畸变屈曲和整体屈曲破坏.

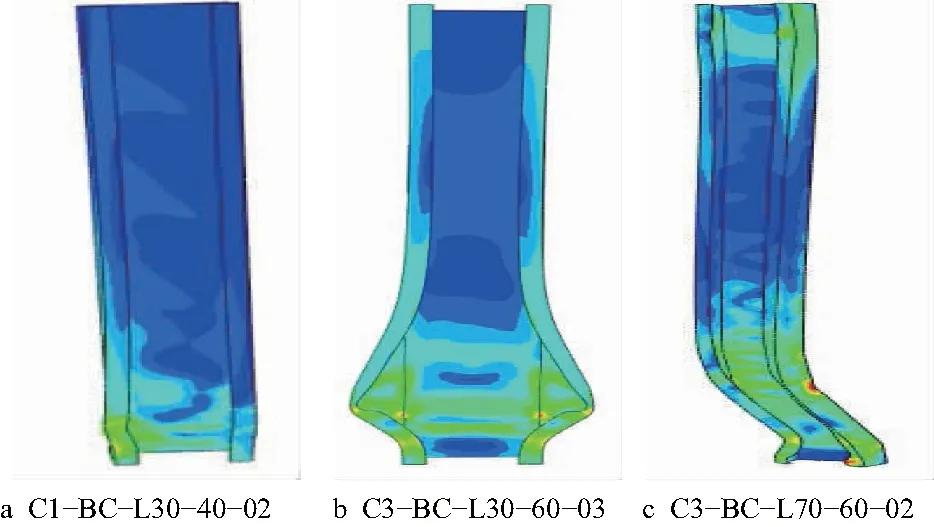
图6 破坏模式分析

由图6可知,构件C1-BC-L30-40-02的腹板呈现波纹状,表明构件最终发生局部屈曲失稳破坏.大量的有限元分析结果显示,①发生局部屈曲破坏的构件大多为宽厚比较大的短柱和中长柱.构件C3-BC-L30-60-03的柱脚腹板鼓起、下端翼缘外扩,表明构件最终发生畸变屈曲失稳破坏.②发生畸变屈曲破坏的构件大多为宽厚比较大、卷边较小的中长柱.构件C3-BC-L70-60-02发生挠曲变形,表明构件最终发生整体屈曲破坏.③发生整体屈曲破坏的构件大多为宽厚比较小的长柱.构件C1-BC-L30-40-02的滞回曲线形状饱满,刚度退化较慢,表明发生局部屈曲破坏的构件具有很好的耗能能力(图7);构件C3-BC-L30-60-03的滞回曲线较饱满,在出现屈曲后仍具有较大的承载力,表明发生畸变屈曲破坏的构件仍能保持较好的抗震性能;构件C3-BC-L70-60-02的滞回曲线相对不饱满,刚度退化较快,表明发生整体屈曲构件的耗能能力较差,实际工程中要避免此种屈曲模式的发生.

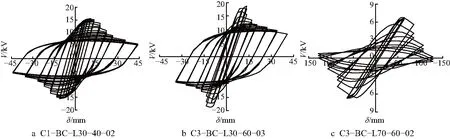
图7 滞回曲线分析

3.2 延性

参考JGJ/T 101—2015[15],以构件骨架曲线退化阶段承载力下降至最大承载力85%时所对应的位移作为构件的破坏位移.笔者采用位移延性系数μ描述构件的延性,计算公式:

μ=Δu/Δy,

(2)

式中:Δu为构件的破坏位移,指骨架曲线荷载峰值下降15%时对应的位移;Δy为构件的屈服位移,通过等能量法根据骨架曲线计算得到.

大部分构件的μ小于3(表3),μ随着构件的长细比或轴压比的增大呈现降低趋势,其中,构件的轴压比对μ影响显著.

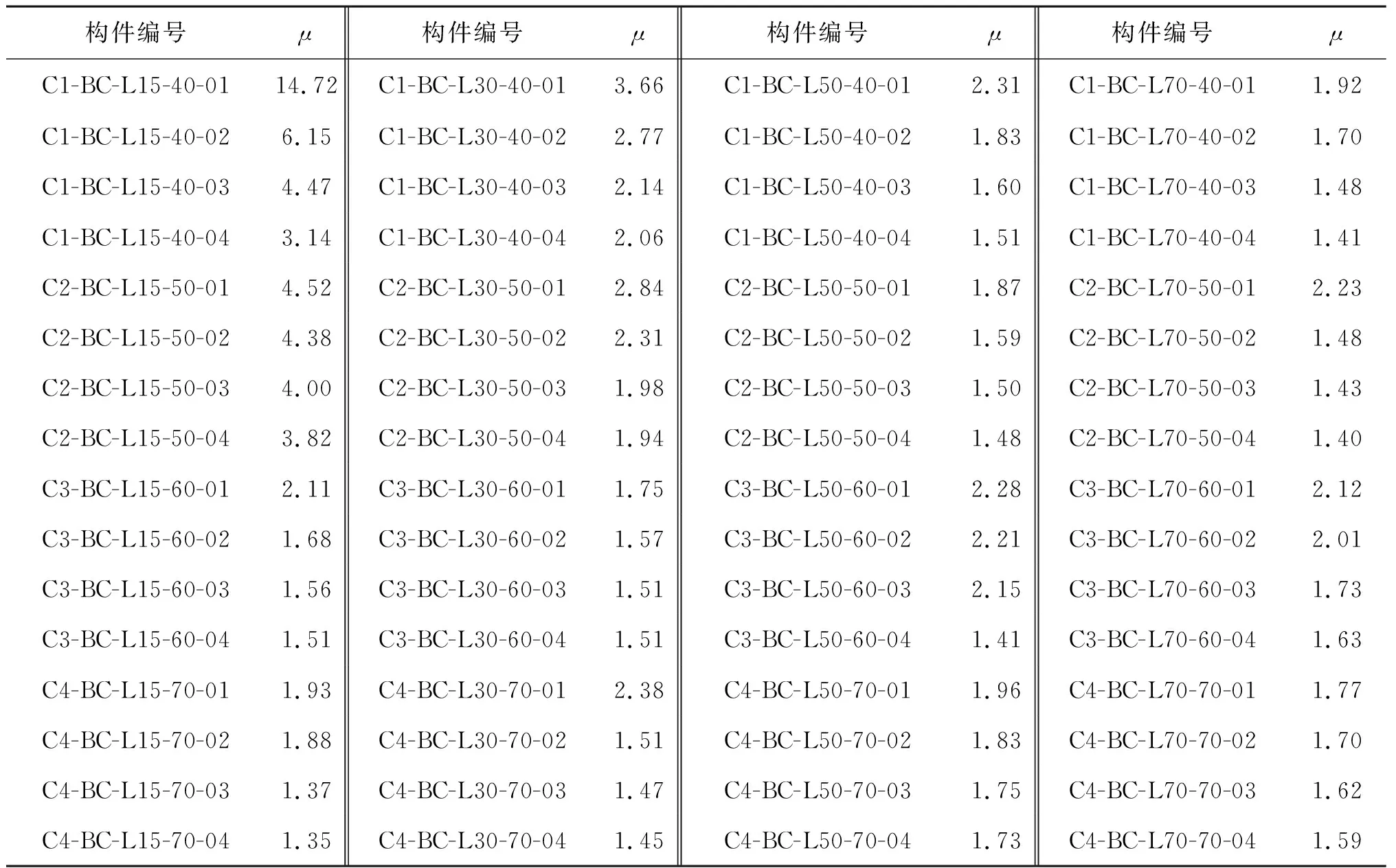
表3 构件的延性比较

3.3 耗能能力

构件的耗能能力可通过滞回曲线所包围的面积和形状来衡量[16].图8为滞回环示意图.笔者通过等效黏滞阻尼系数he衡量构件的耗能能力,计算公式:

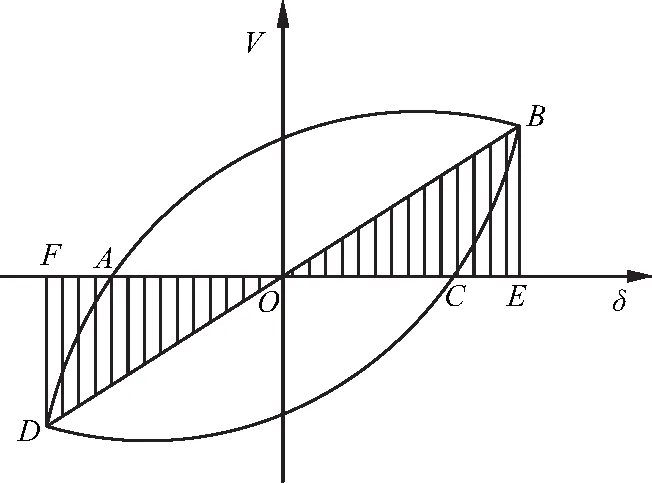
图8 滞回环示意图

(3)

由(3)式计算得到he与加载级数i的关系曲线(图9).

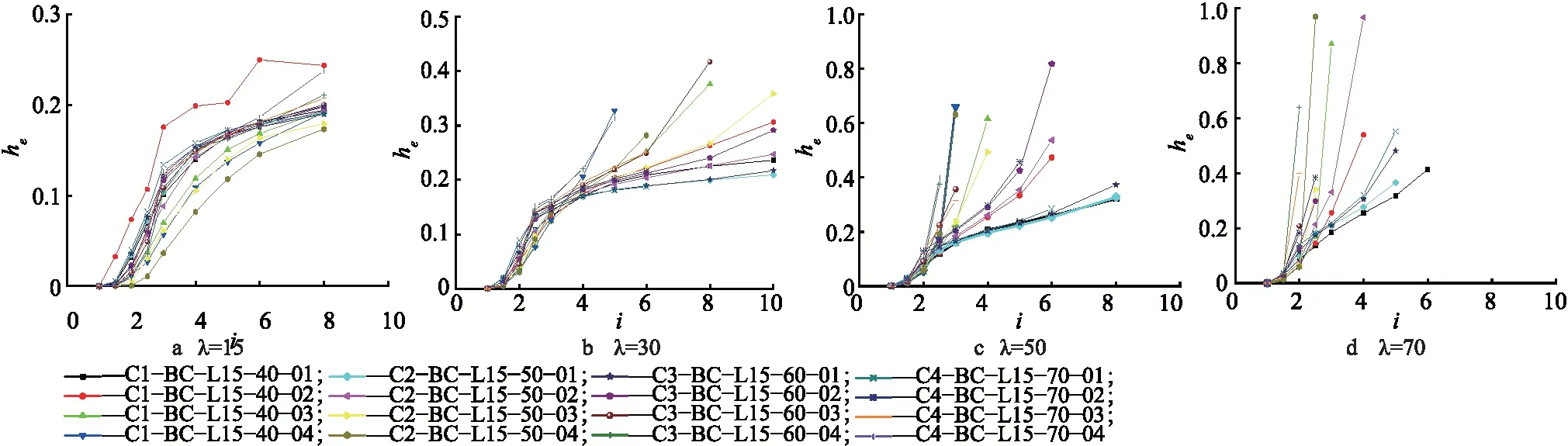
图9 等效黏滞阻尼系数与加载级数的关系

由图9可知,长细比越大,构件的he随i变化越快;宽厚比越大,构件越早出现破坏变形.冷弯薄壁型钢槽形截面压弯构件的he随着i的增加而增大,并在加载后期增加迅速,表明该类构件在承载力逐渐丧失的情况下仍然具有一定的耗能能力,抗震性能较好;构件在破坏状态下仍具有一定的后期耗能性.

3.4 刚度退化

通过割线刚度Ki描述刚度退化情况[17],割线刚度的计算公式:

(4)

式中,Ki为第i次加载级的割线刚度;Fi为第i次加载级中第1次循环的荷载峰值;δi为第i次加载级中第1次循环的荷载峰值对应的位移.图10为Ki与i的关系.由图10可知,在构件的长细比相同时,轴压比越大构件的初始割线刚度越小,刚度退化越快,越不利于结构抗震;在构件的长细比相同时,宽厚比较大的构件割线刚度较小,因此割线刚度随构件的长细比增大而减小.

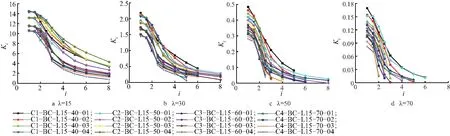
图10 割线刚度与加载级数的关系

3.5 骨架曲线

3.5.1长细比的影响 通过有限元模型得到相同宽厚比和轴压比、不同长细比下冷弯薄壁型钢槽形截面压弯构件的骨架曲线(图11,限于篇幅仅给出部分构件的骨架曲线变化图).图11中,Mp为构件全截面塑性弯矩,相对转角φ=δ/L(%),L为构件长度.

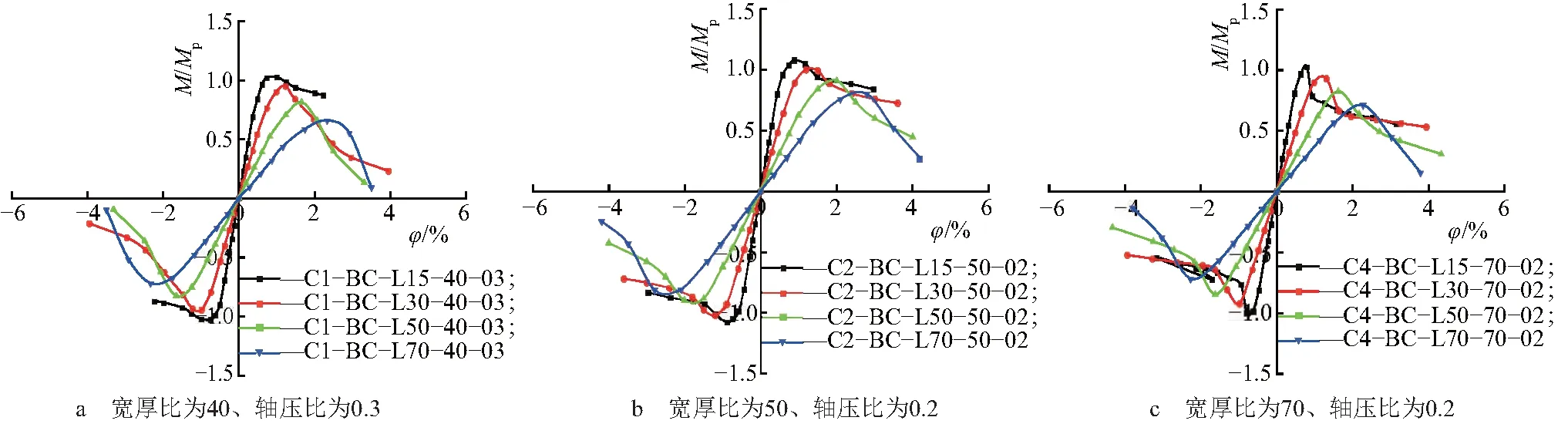
图11 构件长细比的影响

由图11可知,对于相同截面、不同长度的构件,转动相同的角度,不同长细比的构件所能承受的塑性弯矩相差很大.长细比越大,构件的塑性弯矩和初始弹性刚度越小,承载力越低,耗能能力越差,刚度退化越快.

3.5.2宽厚比的影响 图12为相同长细比和轴压比、不同宽厚比下构件的骨架曲线.由图12可知,在构件的长细比和轴压比相同的条件下,对于不同宽厚比的构件,在滞回加载初期,构件处于弹性阶段,尚未屈服,骨架曲线几乎重合.在构件屈服阶段,对于宽厚比较大的构件,骨架曲线的强化阶段变短.构件的强度在达到极限承载力后迅速下降,转动能力变小,说明构件的延性系数小,极易发生脆性破坏.表明构件的宽厚比影响其延性和承载力.当构件的宽厚比控制在40～70,构件具有较好的滞回性能.

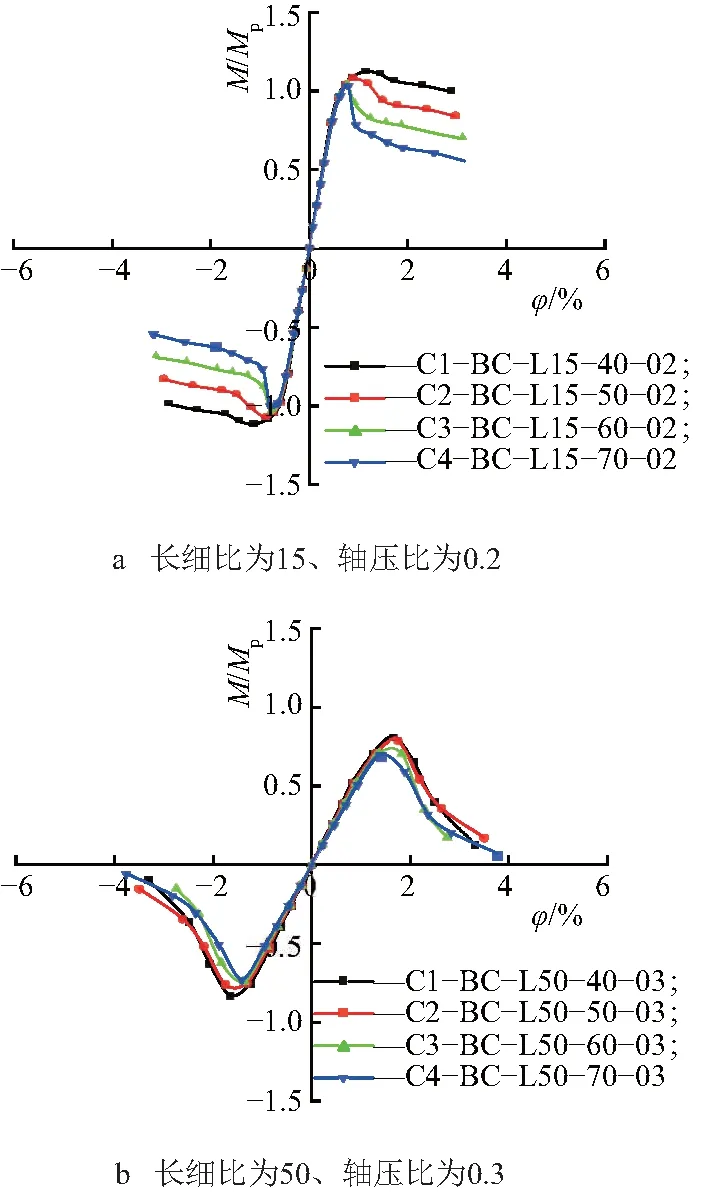
图12 构件宽厚比影响

3.5.3轴压比的影响 图13为相同构件在轴压比发生变化时的骨架曲线.由图13可知,对相同构件施加不同压力,在加载初期,骨架曲线的斜率相近,说明构件的轴压比对初始刚度影响不大.在加载后期,由于静轴力不同,4个相同构件的骨架曲线不仅峰值位置相差较大,而且后期的转动能力相差较大.说明构件的轴压比对承载力和转动能力的影响较大,轴压比越大,塑性弯矩和延性越小,耗能能力越差.

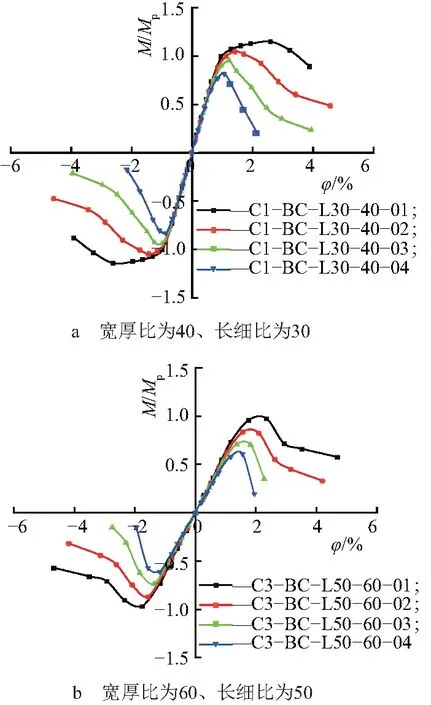
图13 轴压比的影响

3.5.4材料屈服强度的影响 图14为材料屈服强度对相同截面参数下冷弯薄壁型钢槽形截面压弯构件的影响.由图14可知,材料屈服强度增大,构件的初始弹性刚度减小,极限承载力明显提高,但由于自身的强度难以充分发挥,难以达到塑性弯矩.材料屈服强度的增大对构件承载力达到峰值后的刚度退化速率影响不大.

图14 材料屈服强度的影响

4 结论

1)对于短柱,主要发生局部屈曲破坏;对于中长柱,当其翼缘与卷边比较大时,易发生畸变屈曲破坏.但对于发生整体屈曲破坏的构件,破坏前可能先发生局部屈曲或畸变屈曲;对于长柱,易发生整体屈曲破坏.

2)构件的长细比越大,延性系数越小;构件的轴压比越大,承受的静轴力越大,延性系数越小.

3)构件的宽厚比、长细比越大,耗能能力越差.冷弯型钢在承载力逐渐丧失的情况下,耗能能力增加,说明其具有一定的后期耗能能力.

4)对于截面参数相同的构件,长细比或轴压比越大,刚度退化越快,越不利于抗震.

5) 合理控制构件的长细比、宽厚比、轴压比,可提高构件的承载力、延性系数、耗能能力,减小刚度的退化速度,从而提高冷弯薄壁型钢槽形截面压弯构件的抗震能力.