二维格微分方程周期强迫波的唯一性
2023-11-09顾宇萌史振霞
顾宇萌, 史振霞
(兰州交通大学 数理学院, 甘肃 兰州 730070 )
近年来, 由于全球气候变化, 许多物种开始慢慢向极地迁移, 为了生存, 它们需以一定速度迁移到适合生存的环境.为了更好地解释迁移对物种生存产生的影响, 学者们开始研究随着栖息地的变化物种的动力学行为[1—5], 从而判断该物种在未来是持续存在还是走向灭绝.如果走向灭绝, 就需要采取保护措施, 这对自然界的生态平衡有重要的现实意义.对这一问题的研究可以追溯到2009年, Berestycki等在文献[1]中应用最大值原理和比较原理研究了方程
ut=Duxx+f(x-ct,u)
(1)
行波解的存在性及解的渐近行为, 从而研究气候变化对种群的影响.
2017年, Hu和Zou在文献[2]中利用上下解方法结合单调迭代技巧证明了反应扩散方程:
ut(t,x)=duxx(t,x)+
u(t,x)(r(x-ct)-u(t,x)),t>0,x∈R
(2)
单调强迫波的存在性, 其中假设增长率r是与时空相关的,r(ξ)连续非减且有界, 并满足r(-∞)<0
2018年, Li等[3]和Wang等[4]利用单调半流方法证明了非局部扩散方程
ut(t,x)=d(J*u-u)(t,x)+
u(t,x)(r(x-ct)-u(t,x)),t>0,x∈R
(3)
行波解的最小波速c*的存在性, 从而证明了强迫波的存在性、唯一性和稳定性以及当c 在种群动力学中, 格微分方程可以描述空间离散斑块环境下种群的增长和入侵过程.温度和季节变化也会对种群动态产生很大影响, 例如, 在一年的时间里,由于低温、缺乏食物或其他原因, 种群的出生率在春天较高、冬天较低. 因此, 研究具有时间周期的格微分方程的行波解及强迫波是具有现实意义的.2021年, Pang和Wu在文献[7]中应用上下解方法结合单调迭代技巧证明了具有时间周期的一维格微分方程 ut(t,x)= d[u(t,x+1)-2u(t,x)+u(t,x-1)]+ u(t,x)(r(x-ct,t)-u(t,x)) (4) 强迫波的存在性, 并应用滑动技巧及比较原理证明了强迫波的唯一性和全局指数稳定性. 在实际生活中, 许多问题的研究通常是在高维空间环境中, 而非一维情形,从而启发了许多学者开始研究二维格微分方程.Zhang和Guo在文献[8]中利用上下解方法及单调迭代技巧证明了二维格微分方程 ui,j-1-4ui.j+f(ui,j),i,j∈Z (5) 单稳行波解的存在性, 并利用Ikehara定理研究解的渐近行为, 从而证明了行波解的唯一性. 二维格微分方程的行波解已经被广泛研究[8,11].从上述结果可以发现, 研究二维空间下迁移对物种生存产生的影响具有重要的理论价值和现实意义.受文献[7]的启发, 本文研究二维格微分方程 ut(x,t)=D[u(x+cosθ,t)+u(x-cosθ,t)+ u(x+sinθ,t)+u(x-sinθ,t)-4u(x,t)]+ u(x,t)(r(x-ct,t)-u(x,t)), (6) 满足边界条件 (7) 的周期强迫波u(x,t)=U(x-ct,t)的唯一性, 其中x=icosθ+jsinθ,i,j∈Z,且θ∈[0,π/2]是波的传播方向,q(t)为空间齐次方程u′(t)=u(t)[r(+∞,t)-u(t)]的唯一正周期解,u(x,t)表示x处t时刻的种群密度,D>0为种群扩散率,c∈R是栖息地变化的速度,r是与时空相关的种群增长率,u(x,t)(r(x-ct,t)-u(x,t))可以理解为种群在栖息地变化时做出的反应.假设r(x,t)满足下列条件: (H)r(ξ,t)是连续函数且关于ξ是非减的, 并且满足-∞ 同时考虑将空间区域分为对种群生存有利的区域(r(x-ct,t)>0)和对种群生存不利的区域(r(x-ct,t)≤0). 首先给出周期强迫波的定义. 定义1若U(ξ,t)满足 Ut=D[U(ξ+cosθ,t)+U(ξ-cosθ,t)+ U(ξ+sinθ,t)+U(ξ-sinθ,t)-4U(ξ,t)]+ cUξ+U(ξ,t)(r(ξ,t)-U(ξ,t)) 及U(ξ,t)=U(ξ,t+ω), 其中ξ=x-ct,c为环境变化的速度, 则称u(x,t)=U(x-ct,t),x=icosθ+jsinθ为方程(6)的周期强迫波. 定理1设条件(H)成立, 对于任意c>-c*,方程(6)存在连接0和q(t)的周期强迫波U(x-ct,t),x=icosθ+jsinθ, 其中 方程(6)周期强迫波的存在性定理可以利用上下解方法并结合单调迭代技巧得到, 其具体证明过程可参考文献[5,7],下面给出其概要. 令V(ξ,t)=U(-ξ,t), 研究下列方程的周期强迫行波解V(ξ,t): Vt=D[V(ξ+cosθ,t)+V(ξ-cosθ,t)+ V(ξ+sinθ,t)+V(ξ-sinθ,t)-4V(ξ,t)]- cVξ+V(ξ,t)(r(-ξ,t)-V(ξ,t)), (8) 满足边界条件 (9) (Vε)t=D[Vε(ξ+cosθ,t)+Vε(ξ-cosθ,t)+ Vε(ξ+sinθ,t)+Vε(ξ-sinθ,t)-4Vε(ξ,t)]+ cε(Vε)ξ+fε(t,Vε) 的解, 且 根据上、下解的形式定义波廓集 其次, 定义算子F:Γ→C(R2,R), 记为 t∈(0,ω],ξ∈R, H(V)(ξ,t)∶=ρV(ξ,t)+D[V(ξ+cosθ,t)+ V(ξ-cosθ,t)+V(ξ+sinθ,t)+ V(ξ-sinθ,t)-4V(ξ,t)]+ V(ξ,t)(r(-ξ,t)-V(ξ,t)), 将方程解的存在性问题转化为算子F的不动点问题. 定理2设条件(H)成立.当c>-c*时, 方程(6)有唯一的连接0和q(t)的周期强迫波U(x-ct,t),x=icosθ+jsinθ. 证明定义正函数g(ξ,t), 使得 g(ξ,t)=g(ξ,t+ω),g(±∞,t)>L, 其中L>0.假设Ui(ξ,t),i=1,2为方程(6)具有相同强迫波速c>-c*的两个强迫波, 并满足Ui(-∞,t)=0,Ui(+∞,t)=q(t),i=1,2. 对于任意的ε>0, 令 Mε∶={m≥1:mU1(ξ,t)≥U2(ξ,t)-εg(ξ,t), ∀(ξ,t)∈R2}, 则显然 对所有的t∈R成立, 故存在常数h使得 因此,Mε≠∅. 令mε=infMε, 则mεU1(ξ,t)≥U2(ξ,t)-ε,∀(ξ,t)∈R2. 对于任意的0<ε1<ε2, 有mε1U1(ξ,t)≥U1(ξ,t)-ε1>U2(ξ,t)-ε2成立.因此,mε1≥mε2, 即mε关于ε是非增的. 情况1 若对于任意ε>0,mε=1, 则m*=1显然成立; 情况2 若存在ε0>0使得mε0>1, 则根据mε关于ε的非增性可知,对于ε∈(0,ε0], 有mε≥mε0>1. 下面证明情况2是不成立的.对于任意的ε∈(0,ε0], 定义 vε(ξ,t)=mεU1(ξ,t)-U2(ξ,t)+ εg(ξ,t),∀(ξ,t)∈R2, 则有vε(ξ,t)≥0,∀(ξ,t)∈R2. 从而显然有 又由mε的定义可知, 存在(ξε,tε)使得 vε(ξε,tε)=0,在(ξε,tε)的任意邻域内vε(ξ,t)≠0. (10) (mε-η)U1(ξ,t)≤U2(ξ,t)-εg(ξ,t),∀(ξ,t)∈R2, 这与mε的定义矛盾. 因此,(10)式成立. 由于vε关于t具有周期性, 故假设tε∈[0,ω]. 此外, 序列{ξε}存在3种可能情况:(ⅰ){ξε}是有界的;(ⅱ){ξε}→+∞;(ⅲ){ξε}→-∞. vt=m*(U1)t-(U2)t= D[v(ξ+cosθ,t)+v(ξ-cosθ,t)+ v(ξ+sinθ,t)+v(ξ-sinθ,t)-4v(ξ,t)]+ D[v(ξ+cosθ,t)+v(ξ-cosθ,t)+ v(ξ+sinθ,t)+v(ξ-sinθ,t)-4v(ξ,t)]+ (11) 0≤vt(ξ*,t*)-D[v(ξ*+cosθ,t*)+ v(ξ*-cosθ,t*)+v(ξ*+sinθ,t*)+ v(ξ*-sinθ,t*)-4v(ξ*,t*)]- cvξ(ξ*,t*)-v(ξ*,t*)[r(ξ*,t*)- (m*U1+U2)]= -D[v(ξ*+cosθ,t*)+v(ξ*-cosθ,t*)+ v(ξ*+sinθ,t*)+v(ξ*-sinθ,t*)]≤0. 因此,v(ξ,t)≡0, 这与v(+∞,t)=(m*-1)q(t)矛盾. 故m*=1, 说明情况2不成立. (ⅱ)若{ξε}→+∞, 则存在ηε>0满足若(ξ,t)∈Ωε∶=(ξε-ηε,ξε+ηε)×[0,ω]成立, 则有 (vε)t=mε(U1)t-(U2)t+εgt= D[v(ξ+cosθ,t)+v(ξ-cosθ,t)+ v(ξ+sinθ,t)+v(ξ-sinθ,t)-4v(ξ,t)]+ c(vε)ξ+mεU1(r(ξ,t)-U1)-U2(r(ξ,t)-U2)+ ε{gt-D[g(ξ+cosθ,t)+g(ξ-cosθ,t)+ g(ξ+sinθ,t)+g(ξ-sinθ,t)-4g(ξ,t)]-cgξ}≥ D[v(ξ+cosθ,t)+v(ξ-cosθ,t)+v(ξ+sinθ,t)+ v(ξ)ξ-sinθ,t)-4v(ξ,t)]+ c(vε)ξ+vε[r(ξ,t)-(mεU1+U2)]+ ε{gt-D[g(ξ+cosθ,t)+g(ξ-cosθ,t)+ g(ξ+sinθ,t)+g(ξ-sinθ,t)-4g(ξ,t)]-cgξ}≥ D[v(ξ+cosθ,t)+v(ξ-cosθ,t)+v(ξ+sinθ,t)+ v(ξ-sinθ,t)-4v(ξ,t)]+ c(vε)ξ+vε[r(ξ,t)-(mεU1+U2)], 其中假设 gt-D[g(ξ+cosθ,t)+g(ξ-cosθ,t)+ g(ξ+sinθ,t)+g(ξ-sinθ,t)-4g(ξ,t)]- cgε-g[r(ξ,t)-(mεU1+U2)]≥0. (12) 对于任意的(ξ,t)∈R2,vε(ξ,t)≥0且根据(10)式知vε(ξε,tε)=0, 故可得 vε(ξε+cosθ,t)+vε(ξε-cosθ,t)+ vε(ξε+sinθ,t)+vε(ξε-sinθ,t)=0. (13) 若mε=+∞, 则根据vε(ξ,t)的定义可知 这与(13)式矛盾.因此, 假设mε∈(1,+∞).令 由于tε∈[0,ω], 存在序列{εn}使得当n→+∞时,εn→0+,tεn→t0,ξεn→+∞,又由(13)式可得 vεn(ξεn+sinθ,t)+vεn(ξεn-sinθ,t)]=4v(+∞,t), 这与v(+∞,t)=(m*-1)q(t0)矛盾. 因此, 当{ξn}→+∞时情况2不成立. 此外需补充构造合适的g(ξ,t)使得(12)式对于任意的t∈R和充分大的|ξ|成立.根据文献[5]定理1.3的相似理论, 可以选择g∈C1,1(R×R)使得g(ξ,t)关于t具有周期性且满足 其中:ξ1<0,使得 r(ξ,t)-(mεU1+U2)≤χ1(t),ξ≤ξ1, ξ2>0, 使得 r(ξ,t)-(mεU1+U2)≤χ2(t),ξ≥ξ2, χ2(t)∶=r(+∞,t)-(mε+1)q(t)+ 显然,对于t∈[0,ω]和ξ<ξ1-cosθ,(12)式成立, 即 gt-D[g(ξ+cosθ,t)+g(ξ-cosθ,t)+ g(ξ+sinθ,t)+g(ξ-sinθ,t)-4g(ξ,t)]- cgξ-[r(ξ,t)-(mεU1+U2)g]= χ(t)g(ξ,t)+D[g(ξ+cosθ,t)+ g(ξ-cosθ,t)+g(ξ+sinθ,t)+g(ξ-sinθ,t)- 4g(ξ,t)]-[r(ξ,t)-(mεU1+U2)]g≥0. 同理可证, 对于ξ<ξ1-sinθ,ξ>ξ2+cosθ,ξ>ξ2+sinθ,(13)式成立.因此对于任意t∈[0,ω]和充分大的|ξ|,(12)式成立. (ⅲ)若{ξε}→-∞, 则对于(ξ,t)∈Ωε, 同样可以得到 (vε)t≥D[vε(ξ+cosθ,t)+vε(ξ-cosθ,t)+ vε(ξ+sinθ,t)+vε(ξ-sinθ,t)-4vε(ξ,t)]+ c(vε)ξ+vε[r(ξ,t)-mεU1+U2]. 应用(ⅱ)中相似的理论同样可以得出矛盾, 从而当{ξn}→-∞时情况2不成立. 综上所述, 情况2不成立, 情况1成立, 即m*=1, 故可知对于任意的(ξ,t)∈R2,有U1(ξ,t)≥U2(ξ,t). 改变U1和U2的位置, 同理可得对于任意的(ξ,t)∈R2,U2(ξ,t)≥U1(ξ,t). 因此,U1≡U2. 证毕. 在研究具有时间周期的二维格微分方程(6)强迫波的唯一性时, 本文采用挤压技巧得到了唯一性定理, 证明了对于任意的c>-c*, 方程(6)有唯一满足边界条件(7)的周期强迫波.
1 预备知识


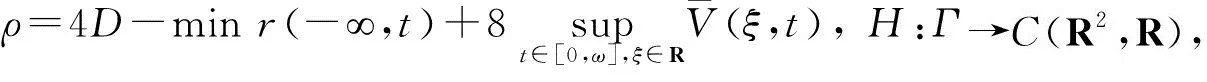
2 周期强迫波的唯一性



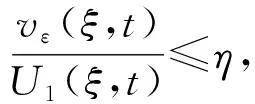


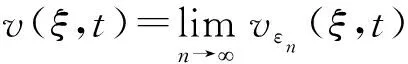
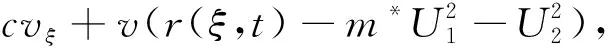

3 结论
