基于时差-即时学习的相关向量机软测量建模研究

金绍琴 唐莉丽 吴菁 李明珠 黄道平

摘要：针对污水处理厂的过程数据时变性较大、非线性较强，传统的离线模型难以应对实际处理过程中的工况变化等问题，提出一种基于时差-即时学习的相关向量机（RVM）模型TD-JIT-RVM。通过时间差分（TD）建模提取过程变量之间的关联关系，采用即时学习（JIT）解决时滞引起的模型退化问题。利用TD-JIT-RVM模型对仿真数据集和真实的工业数据集进行分析，结果表明，该模型在两个数据集中比RVM基础模型的RMSE分别提高了94.59%和82.26%。

关键词：污水处理；时间差分；即时学习；相关向量机；在线软测量

中图分类号：TP 277            文献标志码：A           文章编号：1674-2605（2023）05-0004-10

DOI：10.3969/j.issn.1674-2605.2023.05.004

Research on Soft Sensor Modeling of Relevance Vector Machine Based on  Time Difference-Just in Time

JING Shaoqin¹ TANG Lili¹ WU Jing^1，2 LI Mingzhu² HUANG Daoping³

（1.College of Data Science and Information Engineering， Guizhou Minzu University， Guiyang 550025， China    2.TJ-YZ School of Network Science， Haikou University of Economics， Haikou 570203， China

3.School of Automation Science and Engineering， South China University of Technology，            Guangzhou 510640， China）

Abstract： A relevance vector machine （RVM） model TD-JIT-RVM based on Time Difference-Just in Time is proposed to address the issues of large time-varying and strong nonlinearity of process data in sewage treatment plants， and traditional offline models are difficult to cope with changes in actual processing conditions. Extract the correlation between process variables through Time Difference （TD） modeling， and solve the model degradation problem caused by time delay using just in time （JIT）. The TD-JIT-RVM model was used to analyze the simulation dataset and the real industrial dataset， and the results showed that the RMSE of the model increased by 94.59% and 82.26% compared to the RVM basic model in both datasets， respectively.

Keywords： wastewater treatment; time difference; just in time; relevance vector machine; online soft sensors

0  引言

軟测量技术是通过统计模型、机器学习等方法建立易测变量与目标变量（难测变量）之间的数学关系，并从易测变量推断目标变量数值的一种技术^[1]。软测

量建模方法主要有机理建模和数据驱动建模。与机理建模相比，数据驱动建模先从数据中选取特征，再进行模型训练和优化，无需大量的专业知识和经验来开发模型，更适合具有多样性和多层次性的复杂工业过

程建模^[2-4]。目前，数据驱动软测量技术主要包括主成分回归（principal component regression， PCR）^[5]、偏最小二乘回归（partial least squares regression， PLSR）^[6]、人工神经网络（artificial neural network， ANN）^[7]和支持向量机（support vector machine， SVM）^[8]等。其中，SVM是一种基于统计学习理论的结构风险最小化（structural risk minimization， SRM）原理的机器学习算法^[9]，比ANN具有更好的泛化性能，广泛应用于模式分类和回归估计，但对数据噪声较敏感。1999年，SUYKENS等^[10]提出了基于SVM的最小二乘支持向量机（least squares support vector machine， LSSVM），与ANN相比，它对非线性工艺数据具有更好的泛化性能^[11]，常用于离线数据建模，但不适用于在线数据建模。LYU等^[12]提出的一种基于数据相似性的在线学习技术，可有效地筛选并实时调整输入数据，但该方法计算成本较高，不适合实时应用。

近几年，尽管针对SVM算法的研究有所进展，但也呈现出不适定的问题，如后验概率分布不可计算、惩罚因子C不可估计、核投影需要Mercer条件等。相关向量机（relevance vector machine， RVM）^[13-14]是SVM的贝叶斯替代方案，具有相关向量稀疏、泛化性能好、具备统计解释性的预测结果等特点，明显缓解了不适定的问题^[15]。RVM算法不需要对超参数进行交叉验证，即可实现输出的概率分布计算，且核函数可以任意指定，不受正范式的约束。王春雷等^[16]通过使用组合核函数来提高RVM算法的泛化性，并构建用于预测锂电池使用寿命的模型，但预测结果的拟合程度没有明显变化，并不适用于所有电池。吴菁等^[17]提出一种优化多核RVM模型的方法，增强了RVM中多核函数的建模能力，克服了简单单核函数无法适应强非线性数据的局限性，提高了预测效率和精度，但该模型使用所有过程数据进行训练，无法精准捕捉过程数据的局部动态特征，且数据集中包含冗余信息，约束了模型精度的提高。谭承诚等^[18]开发了一种基于集成RVM的水质在线预测模型，提高了模型的稳定性和可靠性，但计算时间较长。许玉格等^[19]利用自优化理论对核函数进行参数优化，构建基于RVM的多属性核函数预测模型，能够有效地处理复杂的高维数据，且具有良好的准确性，但在线学习能力差，鲁棒性弱。

污水处理的过程数据具有多变量、强干扰、大时滞、强耦合等特点，导致其检测和采样不可避免地存在误差。传统的离线模型用于在线建模时，需实时更新参数以确保模型的有效性。为此，建模过程通常引入在线学习的方法，使软测量模型能够根据新样本实时更新参数，从而在不断变化的数据环境中保持良好的测量精度，同时有效缩减数据的存储成本^[20]。目前，主流的在线软测量建模算法包括递归算法（recursion algorithm， RA）^[4]、移动窗口（moving window， MW）算法^[21]、时间差分（time difference， TD）算法^[22]、即时学习（just in time， JIT）算法^[23]等。其中，RA和MW算法适用于数据漂移的情况；JIT算法适用于采样延迟的情况；TD算法适用于数据延迟和突变的情况^[24]。相比于其他3种算法，TD算法不仅能够有效地抵御输入输出变量的漂移，而且在运行过程中也不需要模型重构。RA、MW、TD这3种算法都是根据时间相关性更新模型，属于时间自适应算法。JIT算法^[27-31]基于空间相关性更新和维护模型，属于空间自适应算法，可以更好地适应生产过程中的复杂现象，且该算法能够对每个样本建立局部模型，能很好地描述过程变量之间的非线性关系。QIN等^[25]提出一种递归偏最小二乘（partial least squares， PLS）算法可有效地解决软测量的退化问题。KANEKO等^[26]提出一种MW算法，使用最近获取的数据来更新模型，能够有效地跟踪过程的动态特征。

本文针对污水处理过程中存在的生化反应复杂、非线性强、运行状态分布不均匀、出水指标误差大等问题，将TD算法和JIT算法结合并引入RVM模型，提出基于时差-即时学习的相关向量机TD-JIT-RVM模型。该模型结合了TD算法和JIT算法的优点，可减少测量数据漂移对模型性能退化的影响，有效捕捉过程数据随时间的动态变化，并实时更新模型参数，保证模型的准确率，解决过程数据漂移、突变、强非线性等导致的模型预测精度随时间下降的问题。

1  理论基础

1.1  RVM模型

RVM模型是一种基于贝叶斯框架的机器学习模型，其通过最大化边际似然获得相关向量和权重^[15]。

最后，通过反TD得到真正的预测值。

1.3  JIT算法

JIT算法作为一种局部建模算法，具有分析复杂非线性数据的能力，它可以根据新的数据不断地更新模型参数，并在实时数据处理中学习和优化模型参数，从而实现数据的动态建模和实时预测。JIT算法流程如图1所示。

JIT算法主要有3个步骤：

1） 建立历史数据库，采集可测量的输入输出数据，这些数据尽可能地覆盖所有的工况条件，并通过减少冗余、归一化等方法进行预处理后，存入历史数据库；

欧式距离公式为

3） 当新的输入数据出现时，转到步骤2）。

2  TD-JIT-RVM模型

在TD-JIT-RVM模型中，TD算法將过程数据划分为一系列时间窗口，对每个时间窗口内的数据进行时间差分处理，可充分反映数据的动态变化，并作为RVM模型的输入；JIT算法先离线采集大量的数据样本，再边建模边预测；RVM模型在离线训练时表现出较好的预测效果。但由于时变问题，在在线应用过程中，RVM模型的性能容易下降。为了保持RVM模型的高性能和及时跟踪状态，引入自适应算法，不断更新模型参数。TD-JIT-RVM建模由2个阶段组成：

1） 离线训练阶段，先对历史数据进行预处理，利用TD算法将预处理后的数据转换为一阶差分向量，作为RVM模型的输入，训练好模型参数，并保存该模型参数用于后续的在线监测；

2） 在线监测阶段，JIT算法通过历史数据的输出特征提取在线数据的特征，模型参数在同步在线建模状态下不断更新，以保证模型的正常运行和性能稳定。TD-JIT-RVM建模过程和框架分别如表1、图2所示。

3  案例分析

3.1  BSM1案例分析

基准仿真1号模型（benchmark simulation model No.1， BSM1）是一个用于模拟和评估污水处理系统的基准平台^[26]，其涵盖了一个完整的污水处理系统，包括入水、生物反应池、二次沉淀池、出水处理等环节。通过BSM1可以更加准确地模拟和评估不同污水处理系统的性能。BSM1平台污水处理原理如图3所示。

BSM1仿真数据集包含14天的3种（晴天、雨天、暴雨天）天气数据，每15 s采样一次，共有1 344组样本数据。其中，前1 000组样本数据用于模型训练，剩余344组样本数据用于在线测试。BSM1仿真数据集中，前7天的数据较为平稳，BOD₅含量变化较小，从第7天开始发生降雨，污水流量大幅增加，使相应的悬浮固体浓度等变量增加，导致出水变量BOD₅含量变化显著。这对在线建模提出了挑战，TD-JIT-RVM模型需连续几天不断地更新状态，同时提供目标变量的准确预测。本文选择的辅助变量与文献[26]一致。工业现场通过传感器等仪器采集的数据易受生产环境、仪器精度、测量方法等影响，数据集维数存在差异，通过零均值可标准化这些数据，如公式（16）所示。

采用预测BOD₅的均方根误差RMSE、预测值与实际BOD₅值的均方根误差以及相关系数r来评估模型性能。

为验证TD-JIT-RVM模型的性能，本文选择PLS、极限学习机（Extreme Learning Machine， ELM）、SVM 3个基础模型作为对比模型，分别引入TD算法和JIT算法进行软测量建模性能测试分析，模型参数如表2所示（PLS无参数设置），预测结果如图4所示。

由图4可以看出，PLS模型的预测效果较好，但在前期BOD₅波动较大时，RVM模型的预测效果比PLS模型好，说明RVM模型在非线性建模中比PLS模型具有更好的跟踪性能，PLS模型更适用于线性预测，这是因为PLS是一个线性模型，不能提取非线性数据特征；ELM是一个前馈神经网络，非线性处理能力比PLS好，但是模型泛化能力较弱，无法很好地控制模型的复杂度，对于小样本数据集，容易出现过拟合的情况，模型在新数据上的表现可能会受到影响；SVM在小样本数据集上泛化能力表现出色，但其性能受核函数的影响较大，且核函数必须符合Mercer条件；RVM无需满足Mercer条件，能够设立多种核函数，相对于SVM算法更具灵活性，且RVM更为稀疏，试验时间更短，更适合于在线检测。

在4个基础模型中分别引入TD算法和JIT算法，图5  对比模型预测结果如图5所示。

由图5可以看出，ELM、PLS、SVM、RVM  4個基础模型的预测精度都得到了有效提升。因为这4个基础模型都是全局离线模型，在线应用时，模型参数没有得到及时更新，难以适应时变过程，但引入TD-JIT算法后，采用即时自适应微调策略，根据查询样本动态实时更新模型参数，可以选择最相关的标记样本来快速微调模型到最新的进程运行状态。模型预测结果对比如表3所示。

由表3可以看出，引入TD算法和JIT算法后的模型比4个基础模型的预测精度分别提升了91%、423%、93%以及94%，且TD-JIT-RVM模型的预测精度高于其他7个模型。这是因为TD算法通过比较当前时刻的数据与前一时刻的数据之差来提取变量之间的动态关系。JIT算法通过局部建模，动态地更新模型参数，使得模型能够快速地适应实时数据的变化，两者结合，使基础模型不仅拥有更好的鲁棒性和自适应性，且更适用于污水处理过程中的复杂性和不稳定性。对比文献[27]，本文提出的TD-JIT-RVM模型优于对比模型，且具有较高的稳定性。

3.2  UCI真实数据实验分析

为进一步测试TD-JIT-RVM模型的性能，采用UCI真实数据集进行实验分析^[26]。该数据集从西班牙巴塞罗那市某个污水处理厂收集，为方便阐述，简称UCI数据集。该污水处理厂的污水处理工艺为活性污泥法，处理过程图如图6所示。其中包含来自不同时间段的污水水样数据和多个水质指标，如pH值、COD（化学需氧量）、BOD（生化需氧量）、溶解氧、氨氮等。数据采集的频率为每隔一天采集1次，采集的数据中包括38个与污水生化系统中有机物和微生物相关的指标变量。

UCI数据集经过前期预处理^[32]共包括400个样本数据。其中，前200个样本数据训练模型，剩余的200个样本数据验证模型的性能。辅助变量的选择与文献[32]一致。先对样本数据进行均值归一化预处理，再利用预处理后的数据构建BOD₅软测量模型。

选用PLS、ELM、SVM 3个模型作为对比模型，分别引入TD算法和JIT算法进行软测量建模性能测试分析，模型参数与BSM1案例一致，相似因子d= 14，预测结果如图7所示。

由图7可以看出，4个基础模型的前期追踪效果较差，特别是PLS模型，这是由于UCI数据为强非线性数据，虽然PLS模型可以引入非线性因素来提高模型的拟合度，但拟合能力不足；ELM采用的单层随机投影（single layer random projection， SLRP）神经网络结构无法充分拟合数据，且污水数据较少，无法保证其泛化能力，导致模型预测精度低，追踪效果差；相较于PLS和ELM模型，SVM模型可以处理高维数据、非线性数据和小样本数据，且具有良好的泛化能力，但SVM模型需要选择的参数较多，如核函数类型、核函数参数、惩罚因子等，不同的参数组合会对模型性能产生不同的影响，对于比较复杂的污水强非线性数据集，参数选择的难度较大且需要大量的实验，费时费力；相较于SVM模型，RVM模型可以使用更少的支持向量来拟合数据，从而简化模型并提高计算效率。与其他机器学习方法相比，RVM的结果易解释，更容易应用于真实数据。

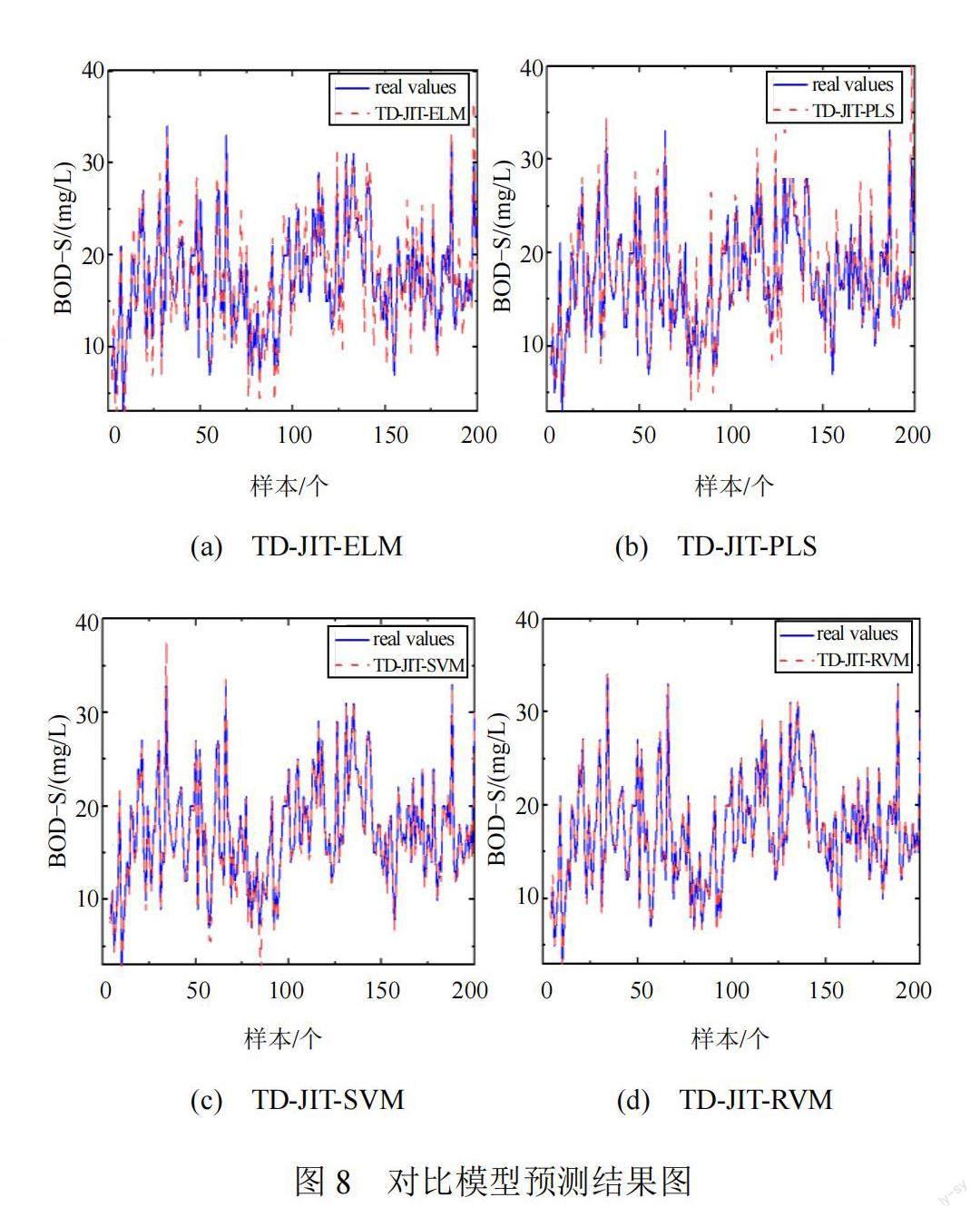
對比模型的预测结果如表4和图8所示。

由表4可知，TD-JIT-ELM、TD-JIT-PLS和TD- JIT-SVM模型的预测结果没有TD-JIT-RVM模型效果好。与RVM模型相比，TD-JIT-RVM模型的RMSE提高了82.26%，这是因为TD算法在分析强非线性数据时，采用一阶差分算法，不需要对状态空间或动作空间进行显式建模或者假设线性关系；相反，它能够根据前一个数据自动调整学习状态，且基于数据的特征和结构自适应地调整模型的参数和结构，RVM结合2种算法的优势则可以更好地捕捉变量之间的非线性关系。

4  结论

本文提出的TD-JIT-RVM模型，能够在实时数据处理中学习和优化模型参数，从而实现数据的动态建模和实时预测。通过2个案例分析得出，对比RVM模型，在加入TD算法和JIT算法后，BSM1案例中的RMSE提高了94.59%，UCI案例中的RMSE提高了82.26%，验证了该模型的有效性。然而，本文所提在线模型的参数更新时间较长，下一步工作将引入快速边际似然算法来加快模型参数的更新速度。

参考文献

[1] JIANG Y， YIN S， DONG J， et al. A review on soft sensors for monitoring， control， and optimization of industrial processes[J]. IEEE Sensors Journal， 2020，21（11）：12868-12881.

[2] KADLEC P， GRBI? R， GABRYS B. Review of adaptation mechanisms for data-driven soft sensors[J]. Computers & Che-mical Engineering， 2011，35（1）：1-24.

[3] SUN Q， GE Z. A survey on deep learning for data-driven soft sensors[J]. IEEE Transactions on Industrial Informatics， 2021， 17（9）：5853-5866.

[4] SOUZA F A A， ARA?JO R， MENDES J. Review of soft sensor methods for regression applications[J]. Chemometrics and Intelligent Laboratory Systems， 2016，152：69-79.

[5] SEDGHI S， SADEGHIAN A， HUANG B. Mixture semisu-pervised probabilistic principal component regression model with missing inputs[J]. Computers & Chemical Engineering， 2017，103：176-187.

[6] DONG J， ZHANG K， HUANG Y， et al. Adaptive total PLS based quality-relevant process monitoring with application to the Tennessee Eastman process[J]. Neurocomputing， 2015，154： 77-85.

[7] HINTON G E， SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science， 2006， 313（5786）：504-507.

[8] NI J， ZHANG C， YANG S X. An adaptive approach based on KPCA and SVM for real-time fault diagnosis of HVCBs[J]. IEEE Transactions on Power Delivery， 2011， 26（3）： 1960-1971.

[9] VAPNIK V. The nature of statistical learning theory[M]. Sprin-ger Science & Business Media， 1999.

[10] SUYKENS J A K， VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters， 1999， 9：293-300.

[11] GE Z， SONG Z. Nonlinear soft sensor development based on relevance vector machine[J]. Industrial & Engineering Che-mistry Research， 2010，49（18）：8685-8693.

[12] LYU Y， YANG T， LIU J. An adaptive least squares support vector machine model with a novel update for NOx emission prediction[J]. Chemometrics and Intelligent Laboratory Sys-tems， 2015，145：103-113.

[13] TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of machine learning research， 2001， 1（Jun）：211-244.

[14] WANG J， QIU K， WANG R， et al. Development of soft sensor based on sequential kernel fuzzy partitioning and just-in-time relevance vector machine for multiphase batch processes[J]. IEEE Transactions on Instrumentation and Measurement， 2021，70：1-10.

[15] CHEN C， WANG Y， ZHANG Y， et al. Indoor positioning algorithm based on nonlinear PLS integrated with RVM[J]. IEEE Sensors Journal， 2017，18（2）：660-668.

[16] 王春雷，赵琦，秦孝丽，等.基于改进相关向量机的锂电池寿命预测方法[J].北京航空航天大学学报，2018，44（9）：1998- 2003.

[17] 吴菁，刘乙奇，刘坚，等.基于动态多核相关向量机的软测量建模研究[J].化工学报， 2019，70（4）：1472-1484.

[18] 谭承诚，于广平，邱志成.基于集成相关向量机的水质在线预测模型[J].计算机测量与控制，2018，26（3）：224-227.

[19] 许玉格，刘莉，罗飞.基于自优化的多属性高斯核函数相关向量机方法[J].华南理工大学学报（自然科学版），2017， 45（1）： 88-94.

[20] 乔俊飞，孙子健，汤健.面向工业过程软测量建模的概念漂移检测综述[J].控制理论与应用，2021，38（8）：1159-1174.

[21] YAO L， GE Z. Online updating soft sensor modeling and industrial application based on selectively integrated moving window approach[J]. IEEE Transactions on Instrumentation and Measurement， 2017，66（8）：1985-1993.

[22] KANEKO H， FUNATSU K. Discussion on time difference models and intervals of time difference for application of soft sensors[J]. Industrial & Engineering Chemistry Research， 2013，52（3）：1322-1334.

[23] GUO F， XIE R， HUANG B. A deep learning just-in-time modeling approach for soft sensor based on variational autoencoder[J]. Chemometrics and Intelligent Laboratory Sys-tems， 2020，197：103922.

[24] 吳菁.污水处理非稳态特性下核建模方法关键问题的研究[D].广州：华南理工大学，2020.

[25] QIN S J. Recursive PLS algorithms for adaptive data modeling[J]. Computers & Chemical Engineering， 1998， 22（4-5）： 503-514.

[26] KANEKO H， ARAKAWA M， FUNATSU K. Development of a new soft sensor method using independent component analysis and partial least squares[J]. AIChE Journal， 2009， 55（1）： 87-98.

[27] 袁凌玲.面向污水处理过程的软测量若干关键技术研究[D].广州：华南理工大学，2021.

作者简介：

金绍琴，女，1997年生，研究生，主要研究方向：软测量建模及优化等。E-mail： airen_jsq@163.com

唐丽丽，女，1997年生，研究生，主要研究方向：软测量建模及优化等。

吴菁（通信作者），女，1988年生，博士，副教授，主要研究方向：软测量建模、深度学习等。E-mail： ipicq@gzmu.edu.cn

李明珠，女，1983年生，硕士，副教授，主要研究方向：智能检测与控制、软测量建模等。

黄道平，男，1961年生，博士，教授，主要研究方向：智能检测与控制、软测量技术等。