方差风险溢价在波动率预测中的应用
——基于上证50ETF期权
2023-11-09曾灵玉
曾灵玉
(香港中文大学(深圳) 数据科学学院, 广东 深圳 518000)
一、研究背景
2015年2月9日,上证50ETF期权在上海证券交易所正式上市,该期权以上证50指数交易开放性指数基金为标的物,实行仅能在到期日行权的欧式行权方式。
上证50ETF期权对我国金融市场的完善具有重要意义。风险管理方面,我国此前主要通过分散化投资等手段进行风险分散,而50ETF期权则提供了一种风险转移的渠道;价格发现方面,期权市场反映了投资者对未来市场的预期,根据有效市场理论,其能够促进现货市场的价格维持在合理的区间;此外,50ETF期权还提供了未来波动率的信息[1]。
波动率在衍生品定价、组合投资、金融风险度量等领域均有广泛的应用。基于此,本文借鉴国内外学者的丰富经验[2-6],以上证50ETF期权市场作为研究对象,挖掘我国期权市场中有关波动率的信息,以期提升我国市场的预测能力,并为金融监管和金融投资提供参考。
二、研究指标
(一)波动率预测指标
20世纪70年代,Fisher Black和Myron Scholes提出了第一个完整的期权定价模型布莱克-斯科尔斯(Black-Scholes,下文简称BS)模型,许多学者对BS模型推导所得隐含波动率的预测能力和包含的信息量进行了研究,并对BS模型进行了一系列修正以减少隐含波动率预测中的偏差(例如引入高频数据对已实现波动率进行更精确的估计)[7-9]。其结论大多支持隐含波动率较历史波动率而言,是对未来已实现波动率的更有效估计,包含了更多的市场信息。但考虑到现实市场中该模型的部分前提假设并不成立,这些研究难以避免模型自身假定错误所带来的影响。
在前人的研究基础上,Britten-Jones和Neuberger[10]提出了无模型隐含波动率。无模型隐含波动率与具体的期权定价公式无关,是在风险中性条件下基于复制定价法对未来已实现方差进行公平定价。该隐含波动率较传统的BS模型隐含波动率具有多项优势。首先,无模型隐含波动率不基于任何特定模型,不用考虑模型本身错误带来的偏差。此外,无模型隐含波动率所包含的信息源自市场上所有交易中的期权,而BS模型隐含波动率则仅从单个期权中提取信息,因此前者应比后者能更有效地提供信息。
Jiang和Tian[11]进一步完善了Britten-Jones和Neuberger[10]的研究,后者对无模型隐含波动率的计算基于连续价格的假设,前者则证明了在资产存在价格跳跃的情况下结论依旧成立。同时他们针对实际计算中会出现的两类误差——不连续误差和截断误差进行了分析,给出了可忽略误差的临界点。
无模型隐含波动率推出后,大量学者采用不同市场的数据对其波动率预测能力进行了研究。其中,黄薏舟等选择香港恒生指数期权市场作为研究对象,运用了包含回归法和正交检验法检验不同波动率预测指标的信息含量[12]。实证结果表明:一个月的无模型隐含波动率不仅包含了所有历史波动率的信息,还包含了BS模型隐含波动率的信息,是对未来已实现波动率的更有效预测[12]。
然而针对上述波动率预测手段,学界又提出了新的质疑:隐含波动率均是在风险中性的前提假设下所获得,而研究中需要进行预测的未来已实现波动率却是基于现实的观测。因此,若希望将隐含波动率作为对未来已实现波动率的代替,则需要满足波动率风险的市场价格等于0。
(二)方差风险溢价
Carr和Wu量化了作为期权标的物的金融资产的方差风险溢价(variance risk premium,下文简称VRP)[13]。由于方差掉期利率代表已实现方差的风险中性预期值,其提出使用已实现方差与方差掉期率之间的差值来量化方差风险溢价。实证结果表明标准普尔和道琼斯指数的方差风险溢价显著为负。进一步的分析显示,方差风险溢价的绝对值会随着方差的扩大而升高。
Prokopczuk和Wese Simen基于此结论将方差风险溢价应用于波动率预测领域,提出了方差风险溢价调整后的隐含波动率,通过事后已实现波动率指标对事前波动率预测指标进行调整,以探究波动率预测的偏差多大程度上可以归因于风险中性假设和实际市场之间的差别[14]。其选取了美国原油、燃料油和天然气三个能源的期货与期权市场作为研究对象,对无模型隐含波动率(MFIV)进行方差风险溢价调整,实证结果表明在原油和燃料油两个市场中,调整后的波动率预测指标较调整前预测力度上升约6%,但调整后的预测模型仍未完全消除所有的预测偏差。
综上所述,无模型隐含波动率在理论层面较BS模型隐含波动率具有更大的优势,前者对于未来已实现波动率具有更强的预测能力,这一结论在美国能源期权市场、美国金融期权市场及香港股指期权市场已得到验证。但即便无模型隐含波动率是对已实现波动率更好的预测,其仍旧存在一定的偏差。国外学者尝试将这一偏差归因于预测指标的风险中性前提和被预测指标计算时采用的实际市场之间的差别,即波动率风险的市场价格不等于0。基于此,国外学者在美国能源期权市场上,通过方差风险溢价调整有效减小了已实现波动率预测偏差。
三、波动率预测指标构建
(一)研究内容
本文选取了我国最早的场内期权,即上证50ETF期权及其标的50ETF的2015年3月1日至2020年12月31日的数据,构造不同的波动率预测指标,回归拟合不同指标对已实现波动率的预测模型,根据回归结果分析波动率的预测能力与信息含量。具体内容如下:
1.根据已有研究,分别基于50ETF构造已实现波动率(RV)、历史波动率(Hist),基于50ETF期权构造BS模型隐含波动率(BS_IV)、无模型隐含波动率(MFIV),以及VRP调整后的无模型隐含波动率(RMFIV)等波动率指标。
2.通过单变量回归验证不同指标与已实现波动率之间的相关性,检验其是否包含关于未来波动率的信息,尤其关注VRP调整后是否能提高预测指标对未来已实现波动率的解释能力。
3.通过多变量回归验证不同指标的相对信息效率,检验是否存在某一预测指标包含另一指标的全部信息。
本文将研究视角转向国内期权市场,旨在检验VRP在中国市场中对波动率预测的应用效果。在验证各类已经过实证检验的预测指标在我国期权市场的适用性的基础上,同时将VRP的影响加入考虑,探究其是否能同在美国市场一样提升对波动率的预测能力。
(二)数据选取
本文选取2015年3月至2020年12月的上证50ETF期权市场作为研究对象,并构造月度波动率指标进行分析。
考虑到此前针对已实现波动率的预测通常会面临滚动窗口计算已实现波动率而带来的重复观测偏差,本文采用Christensen和Prabhala[15]的建议,选择无重叠数据。计算每一个月份的波动率时,均选取距离该月到期日30天的期权数据,若该日为非交易日,则选取距离该日最近的交易日数据作为替代。用于计算已实现波动率的50ETF交易信息则采用日度数据,以每日的收盘价作为当日50ETF的价格。
此处需特别指出,对于波动率的年化处理均采用实际交易天数除以252天的方式。以计算2015年4月波动率为例,当月到期日为4月22日,选取距离到期日30天的3月23日交易数据进行计算,其间实际交易天数为22天,则计算不同波动率时均采用22除以252天进行年化。
本文中50ETF及其期权的数据均来源于JoinQuant数据库。
(三)指标构建
1.已实现波动率(RV)
本研究依照Prokopczuk和Wese Simen[14]对波动率预测模型研究中的计算方法,将已实现波动率定义为一段时间内对数收益平方和的平方根,并对波动率进行年化处理,公式定义如下:
其中:Ft表示标的资产在t日的价格,并同时将延后一期的已实现波动率定义为历史波动率Histt,即有:
Histt=RVt-1。
2.Black-Scholes模型隐含波动率(BS_IV)
Black-Scholes期权定价模型公式如下:
Ct=St·N(d1)-Ke-r(T-t)·N(d2),
Pt=-St·N(-d1)+Ke-r(T-t)·N(-d2),
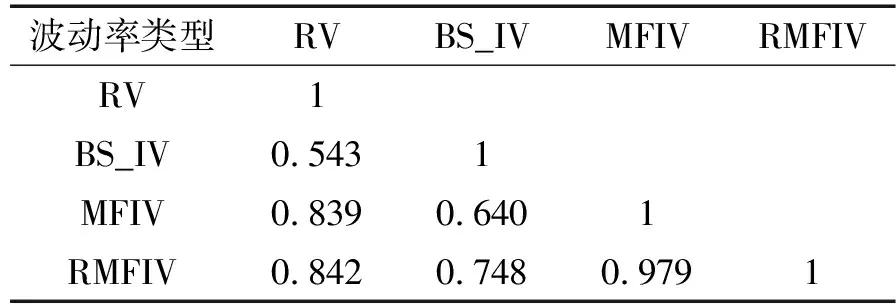
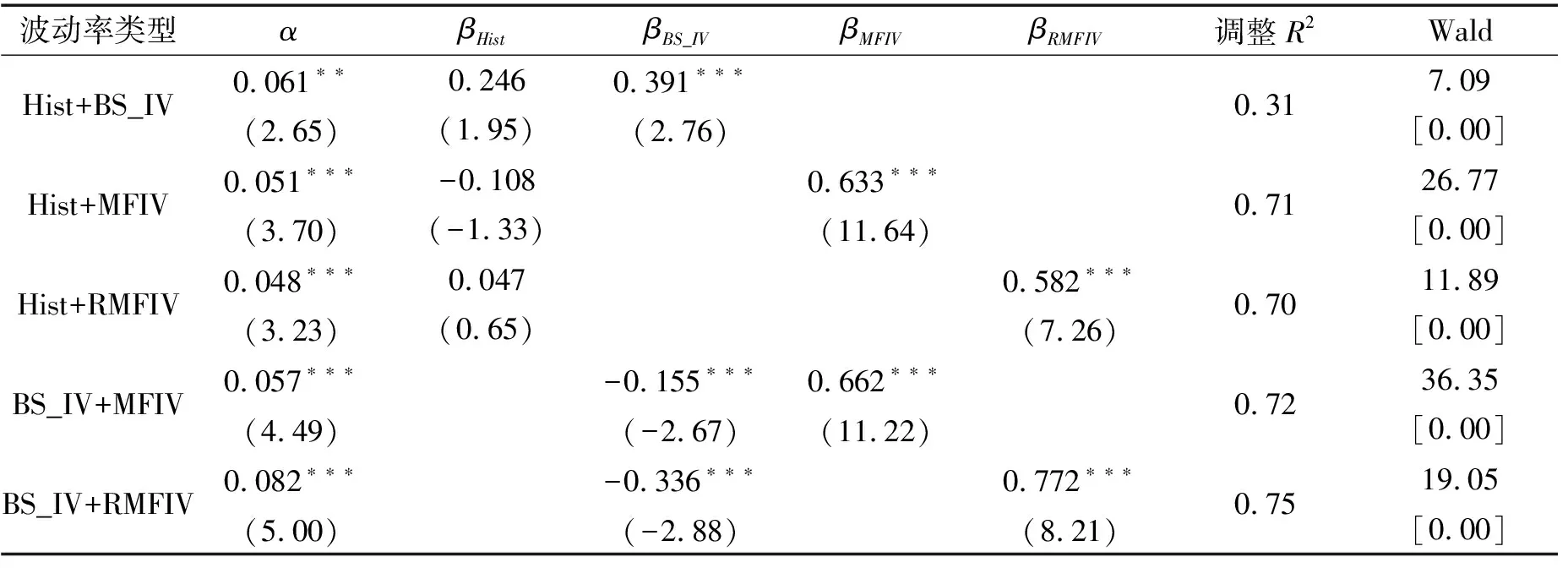
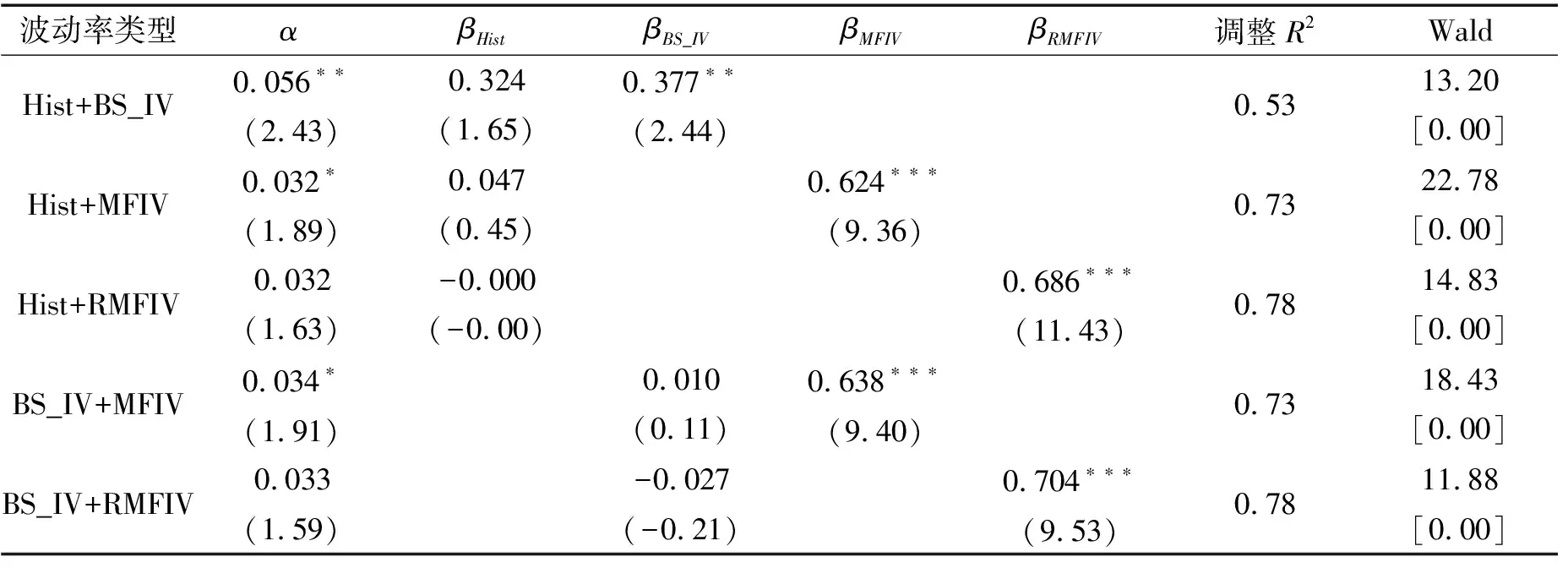
在具体实证中,本文选择价值状态满足0.97St 表1 不同方法下获得的BS_IV与RV的相关系数 由表1可得,BS_IV1与已实现波动率之间的相关系数最高,故本文将其作为最终的BS_IV指标。 3.无模型隐含波动率(MFIV) Britten-Jones和Neuberger[10]推导出了更为简洁、操作性更高的无模型隐含波动率公式,定义如下: 其中:E0表示风险中性条件下的期望,St表示标的资产在t时刻的价格,C(ti,K)表示ti时刻到期、行权价为K的看涨期权价格。对右侧积分开方,即为t1至t2时间段内的无模型隐含波动率。 考虑到现实世界中期权行权价为离散值,计算时需将计算公式进行离散化,公式如下: 基于上式进行计算会面临两类误差:其一,将连续积分进行离散化将会导致一定的不连续误差;其二,实际市场中的期权行权价有一定范围,设为(Kmin,Kmax),若直接在积分中忽略尾部不对其进行计算则会带来截断误差。 针对以上两点,Jiang和Tian[11]通过模拟证明了两种误差是有限的。当离散化后的距离ΔKi<0.35σFt,积分截断点满足Kmin 其中:B(t,T)表示T时刻价值1单位的资产在t时刻的价值,本文采用我国一年期国债收益率的复利形式进行折算。 但实际情况是,我国50ETF期权通常未达到足以忽略两类误差的边界条件,因此需要对数据进行进一步处理。 (1)针对不连续误差 对于实际市场上已有的期权价格和执行价,基于BS公式计算得到其对应的波动率。此后将执行价格间距设定为0.01,通过三次样条插值法,拟合得到市场中不存在的执行价所对应的波动率,即σ=σ(K)。在得到足够多的新执行价K′与波动率σ′后,再次通过BS公式计算得到原本未知的期权价格C′。 (2)针对截断误差 基于以前的研究,本文认为尾部数据(Ft-2σFt,Kmin)∪(Kmax,Ft+2σFt)为常数,且采用截断点Kmin、Kmax处的隐含波动率进行替代。 值得注意的是,Prokopczuk和Wese Simen[14]的研究中计算MFIV时剔除了所有的实值期权,仅采用价外期权进行计算。但考虑到我国50ETF期权市场发展较晚,交易量和可交易的执行价数量偏少,若剔除实值期权将会导致截断点内移,扩大截断误差。故本文计算MFIV时仅删去了不满足期权价格上下限的数据,即看涨(跌)期权价格满足以下两式: max(0,St-Ke-r(T-t))≤C≤St, max(0,Ke-r(T-t)-St)≤P≤Ke-r(T-t)。 4.方差风险溢价修正的无模型隐含波动率(RMFIV) 已有研究通常将方差风险溢价定义为风险中性下和实际中的期望方差的差值,例如Bekaert和Hoerova[16]。 考虑到Carr和Wu[13]的实证结果表明方差风险溢价的绝对值会随着方差的扩大而升高,单纯使用定义为差值的方差风险溢价可能会带来计算上的偏差。 Carr和Wu[13]同时证明了相对方差风险溢价独立于方差水平,因此我们借鉴Prokopczuk和Wese Simen[14]对方差风险溢价的处理,选择相对方差风险溢价作为调整无模型隐含收益率的基准,t至T时间段的相对方差风险溢价RVRP定义如下: 最终本文以此得到方差风险溢价调整后的无模型隐含波动率(RMFIV),t至T时间段内的RMFIV定义为: 值得注意的是,由于上证50ETF上市时间为2015年2月9日,2016年1月以前的MFIV仅通过期权已上市交易日的数据所得VRP进行调整。 表2给出了前述构造的四类波动率的统计特性。可以发现,BS_IV和RMFIV的均值都与已实现波动率较为接近,MFIV则相差略大。 表2 波动率指标的描述性统计 表3给出了四类波动率之间的Pearson相关系数。可以发现RMFIV与已实现波动率的相关性最高,BS_IV与已实现波动率的相关性低于MFIV,这一结果与黄薏舟等[12]的研究是一致的。 表3 四种波动率指标的Pearson相关系数 单变量回归中,本文首先对不同的波动率预测指标与已实现波动率之间的相关性进行论证,即该波动率指标是否包含关于未来波动率的信息。采用OLS回归模型: RVt=α+βfactort+εt, 其中factort表示任一波动率预测指标。 若一个波动率预测指标包含关于未来波动率的信息,则其斜率系数β应当异于0。因此我们检验第一个假设H0:β=0。回归结果如表4,可以发现在单变量回归中所有指标的斜率系数β在1%置信水平上均显著异于0。 表4 单变量回归结果(一) 基于此,我们进一步检验波动率预测指标是否为未来已实现波动率的无偏估计。若一个预测指标为无偏估计,则其回归截距项α=0且斜率系数β=1。因此,我们检验第二个假设H0:α=0,β=1。采用Wald系数检验,在表4的最后一列给出Wald统计量,并在中括号列出其对应P值。 根据表4,四种波动率预测指标均有显著非0的斜率系数,然而对于第二类假设,在所有情况下均拒绝原假设,即在本文基于上证50ETF期权市场中构造所得的MFIV、BS_IV以及历史波动率均为未来已实现波动率的有偏估计。这一结果与Prokopczuk和Wese Simen[14]在美国能源期权市场中所得结果一致。尽管如此,以上结果依旧可以帮助我们验证不同种类预测指标的预测能力。 首先,我们可以发现从Hist到RMFIV四个指标的回归结果中除RMFIV较MFIV截距项略有上升外,其他截距项呈下降趋势,不断向α=0靠近。同时斜率系数均呈上升趋势,不断向β=1靠近,并且RMFIV较MFIV有一个较大的提升。以上证明了RMFIV是对未来已实现波动率的更好估计。 其次,MFIV和RMFIV对应的调整R2显著高于历史波动率和BS_IV,且RMFIV的解释力度较MFIV也略有提升(6%),这一结果同样证明了无模型隐含波动率的优越性。同时,经过方差风险溢价调整的无模型隐含波动率Wald值较调整前略有降低,这一结果支持了此前的理论,即可以通过方差风险溢价调整来减小风险中性假设与实际市场的差异带来的预测偏差,进一步提升无模型隐含波动率对已实现波动率的预测能力。 多变量回归中,本文主要针对不同波动率预测模型的相对信息效率进行研究。此前的研究中,Prokopczuk和Wese Simen[14]与黄薏舟等[12]均得出了无模型隐含波动率包含了所有BS模型隐含波动率的信息这一结论。本小节则沿用以上文献的研究方法,采用多变量回归比较指标的相对信息效率。考虑回归模型: RVt=α+βHistHistt+βBSIVBSIVt+βMFIVMFIVt+βRMFIVRMFIVt+εt。 以研究BS_IV和MFIV所包含的相对信息量为例: (1)若BS_IV与MFIV均不包含任何未来波动率信息,则应有βBS_IV=βMFIV=0; (2)若BS_IV与MFIV包含相互独立的未来波动率信息,则应有βBS_IV≠0且βMFIV≠0; (3)若BS_IV与MFIV包含了完全一样的信息,则βBSIV与βMFIV无法被识别; (4)若BS_IV与MFIV均包含未来波动率的信息,但MFIV完全包含了BS_IV的所有信息,则应有βBSIV=0且βMFIV≠0。 基于此,我们回归结果如表5。斜率系数采用Wald系数检验,在表5的最后一列给出Wald统计量,并在中括号中列出其对应P值。 表5 多变量回归结果(一) 根据表5,虽然Wald检验拒绝了所有的假设,但考虑到本文假设在验证一个指标包含另一个指标的全部信息时包含了该指标为无偏估计这一默认前提,而在上一小节中我们已发现上证50ETF期权市场的四个波动率指标均为有偏估计,故可能由此导致假设检验的Wald值较高。但仍可以通过表内的其他信息对波动率的信息含量进行验证。 2.回归中的原假设依次为:α=0,β_Hist=0,β_(BS_IV)=1;α=0,β_Hist=0,β_MFIV=1;α=0,β_Hist=0,β_RMFIV=1;α=0,β_(BS_IV)=0,β_MFIV=1;α=0,β_(BS_IV)=0,β_RMFIV=1。 根据前三项回归模型可以发现,当历史波动率Hist与其他三种波动率进行多元回归时,其结果均不能拒绝βHist=0这一假设,且斜率系数较Hist单变量回归明显降低,向βHist=0靠近。同时较单变量回归的调整R2(0.33),在加入了两种无模型隐含波动率后模型的R2发生了显著提升(0.71、0.70),但较MFIV与RMFIV自身的单变量回归并未提升或仅微弱提升模型解释效率(0.70、0.76)。基于以上分析,可以认为,BS模型隐含波动率和无模型隐含波动率包含了Hist的所有信息。 同理,根据后两项回归模型,当BS_IV与MFIV、RMFIV进行多元回归时,均在1%显著水平下拒绝βBS_IV=0与βMFIV=0或βRMFIV=0的假设,因此不能得出无模型隐含波动率包含BS模型隐含波动率或相反的结论,这与Prokopczuk和Wese Simen[14]与黄薏舟等[12]的结果相悖。 本文分析出现以上结果的原因可能是我国市场起步较晚尚未成熟。较美国能源期货期权市场和香港恒生指数期权市场,上证50ETF期权市场起步较晚,在较长的一段时间内交易量都处于较低水平,难以反映市场的整体信息。同时,由于MFIV的计算涉及截断误差与不连续误差的处理,上证50ETF期权的行权价范围较小、相邻行权价价差较大,都会影响MFIV构造的精确度。根据已有研究,RMFIV需要使用过去一年内的波动率风险溢价进行调整,而50ETF期权2015年2月才正式推出,这也会在一定程度上导致2016年以前指标的估计偏差。同时,研究样本区间包含了我国2015年与2016年这一股灾时期,股市震荡以及股灾期间政府的救市行为也会对期权市场的波动率特征造成一定影响。上述原因可能会导致两类无模型隐含波动率未能包含BS模型隐含波动率的全部信息。 考虑到上证50ETF期权市场在2017年以前的交易量处于较低水平,流动性缺乏可能会一定程度上影响期权市场的信息传递,导致波动率预测指标与实际波动率之间的偏离。因此,本小节选取2017年以后的数据,重复前述的实证工作,检验在更高的市场活跃度下各类指标是否具有稳健性。 表6和表7分别给出单变量回归和多变量回归结果。 表6 单变量回归结果(二) 表7 多变量回归结果(二) 根据表6可以发现,采用2017年以后的市场数据,Hist和BS_IV的调整R2发生了显著提高,MFIV和RMFIV也略有提升。参数估计方面,四种波动率指标的斜率系数更加接近β=1这一目标,截距项则更接近α=0,且在1%的显著性水平下BS_IV、MFIV和RMFIV已无法拒绝截距项为零这一假设。即,较全时间段的期权市场,2017年后四种波动率预测指标更接近已实现波动率的无偏估计。 2.回归中的原假设同表5。 再根据表7给出的回归结果,对高活跃度市场内波动率预测指标的能力进行进一步分析。前三项回归模型所得结果与全时间段市场的基本一致:在回归模型中加入Hist变量并不会显著提高单变量模型下的调整R2,Hist的拟合斜率系数明显降低,且均不能拒绝βHist=0的假设,即BS_IV、MFIV和RMFIV包含了Hist的所有信息。 但BS隐含波动率与无模型隐含波动率的多元回归则与此前的结果相异。根据后两项多元回归,可以发现即使在2017年后的市场中BS_IV对于已实现波动率的预测能力已得到显著提高的情况下,与MFIV、RMFIV的多元回归中其斜率系数βBS_IV绝对值更逼近于0,统计学上无法拒绝βBS_IV=0的假设。且加入BS_IV后较MFIV、RMFIV单变量回归的调整R2并未改变(均为0.73、0.78),即通过选择2017年后的期权市场数据,得到了两类无模型隐含波动率包含了BS模型隐含波动率的全部信息这一结论。 基于2015年3月至2020年12月的上证50ETF期权市场,本文构造了已实现波动率(RV)、历史波动率(Hist)、BS模型隐含波动率(BS_IV)、无模型隐含波动率(MFIV)、方差风险溢价调整后的无模型隐含波动率(RMFIV)四类波动率预测指标,分析其对未来已实现波动率(RV)的预测能力。实证结果如下: 1.采用上证50ETF期权上市以来的全时间段数据 预测偏差:在50ETF期权市场中四种波动率均为有偏估计,但Hist、BS_IV、MFIV、RMFIV的预测偏差逐次减小,解释力度逐次增加,其中RMFIV为已实现波动率的最佳预测。 相对信息含量:BS_IV、MFIV、RMFIV均包含了Hist的全部信息,但MFIV、RMFIV并不包含BS_IV的全部信息。 2.采用市场具有更高活跃度的时期,即2017年后的市场数据 预测偏差:Hist、BS_IV、MFIV、RMFIV的预测偏差较全时间段均有所减弱,且RMFIV依旧为已实现波动率的最佳预测。 相对信息含量:高活跃度的市场下构造所得的MFIV与RMFIV成功囊括了BS_IV的全部信息,侧面验证了期权市场对信息传递的作用。 通过上述结果,成功证明了波动率预测偏差中的一部分来源于风险中性假设与实际市场之间的差别,而利用方差风险溢价进行调整可以减小这一偏差。 第一,可以适当扩大观测窗。当前在数据选取时仅选择了距离期权到期日30天的数据,舍弃了到期月内的其他期权交易信息;同时,研究仅针对当月到期期权的波动率进行预测分析,后续可加入次月到期期权的波动率等。 第二,针对消除波动率预测偏差进行进一步研究。实证结果表明方差风险溢价可以有效减少风险中性假设下波动率的预测偏差,但并不能完全消除这一偏差,且RMFIV也并非RV的无偏估计。可在如何进一步改进预测指标以减少预测偏差上开展后续研究。 第三,在市场实践层面,方差风险溢价在投资组合方面具有广泛的应用。例如,方差风险溢价可以对股票收益率进行一定的预测。此外,方差风险溢价对波动率的预测,可以应用于Delata组合交易、Gamma组合交易等各类期权波动率策略。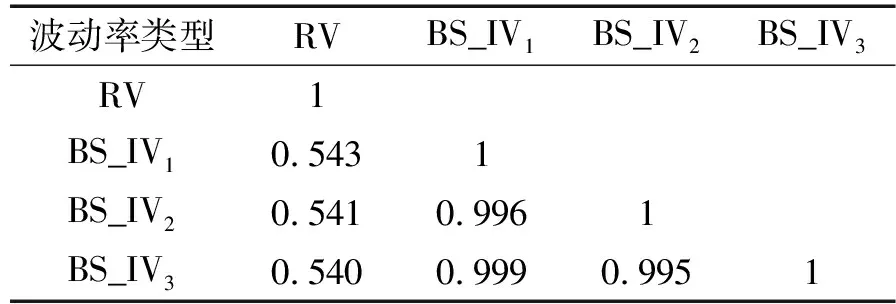
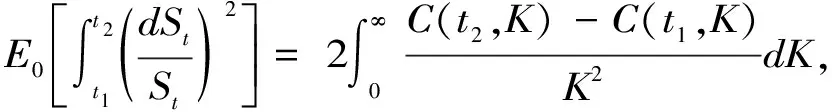
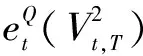
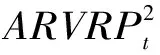
(四)指标描述性统计

四、各指标预测能力的实证分析
(一)单变量回归

(二)多变量回归
(三)稳健性检验

五、结论与建议
(一)结论
(二)建议
