Z字形折叠无人机气动优化设计

孟 宾,张锦康,奚乐乐,杨泽夏,周 宁

(1. 河北科技大学机械工程学院,河北石家庄 050018;2. 河北科技大学电气工程学院,河北石家庄 050018)

随着飞行器产业的不断发展,出现了一种不对称结构的固定翼无人机,这种无人机具有折叠与展开2种形态,展开时形似字母“Z”,因此又被称为Z字形无人机。其具有体积小、质量轻与便携性好等优点,且实现了快速展开起飞,高效执行任务的功能。但受折叠关系的影响,左前翼和右后翼之间存在高度差和机体结构轴向不对称问题,导致其气动特性较为复杂。因此,Z字形无人机的平稳飞行成为了需要解决的首要问题。

为了实现无人机的平稳飞行,白俊强等[1]通过自编程软件,对立椭圆型面后体机身进行了气动分析,相比于圆型面后体机身,提高了航向静稳定性。单栋等[2]对飞机的尾部进行了修型设计,通过适当延长机身与压低尾翼,增加了飞机的纵向和航向静稳定性。王晓璐等[3]采用基于N-S方程的数值模拟方法,对机身上表面、下表面和侧面进行了合理的收缩,减小了飞机的压差阻力和摩擦阻力,改善了飞机的纵向静稳定性。史文博等[4]对螺旋桨安装效应进行研究,适当增大螺旋桨与机身之间的距离,提升了整机升阻比和稳定性。王晓璐等[5]提出双尾撑和倒V尾设计,提高了全机纵向稳定性。为了进一步优化Z字形无人机,张付祥等[6]对Z字形无人机进行了受力分析与实物验证,结果表明合理控制机翼上反角与高度差的大小可以有效抑制飞机的滚转,且Z字形无人机应尽量在小倾角状态下平稳飞行。刘东辉等[7]利用小扰动线性化原理建立纵向线性模型,加入干扰脉冲方式研究模型纵向稳定性,通过程序较好地控制了Z字形无人机的半实物飞行仿真。

由于Z字形无人机的特殊性,以上改进方案对其稳定性具有一定的提升作用,但极易降低舵效和抗风险能力。针对此问题,提出一种基于混合翼型参数化的整机多目标优化方法,开发出整机自动优化流程,用于减小Z字形无人机的滚转力矩和偏航力矩,提高无人机整体气动性能。

1 气动优化模型的构建

1.1 建立整机模型

Z字形无人机的机体结构不对称,机翼分别位于机身顶端和尾端,具有高度差,并且可向机身方向折叠。其垂直尾翼分别位于机身的左右两侧,并且可向平行机身方向折叠。Z字形无人机的俯仰控制舵位于机翼后缘外侧,呈矩形水平分布。方向舵位于垂直尾翼的后缘,呈扇形垂直分布。本研究团队自主设计的Z字形无人机的总体结构如图1所示,其折叠后所占用的空间大大减小,具有便于存放和大批量运输的特点[7]。

图1 Z字形无人机外形图Fig.1 Z-shaped UAV shape

Z字形无人机的外形参数如表1所示。根据其参数值,在SCDM软件中建立整机模型及其流体仿真的外流场。在建模过程中进行脚本文件的录制,通过脚本文件,实现优化模型的自动建立。

表1 无人机外形参数Tab.1 UAV shape parameters

1.2 建立翼型模型

建立优化翼型模型的流程如图2所示,其工作原理是对多个原始翼型进行向量化,然后对向量化后的初始翼型数据点进行加权、求和与归一化,生成新的翼型数据点,通过翼型数据点来生成新的翼型。其中翼型向量化是对翼型的上下表面进行展开处理,使上下表面的翼尖相连,翼根之间的横向距离为2倍的弦长,翼型表面的纵向距离保持不变。

图2 翼型拟合流程Fig.2 Airfoil fitting process

原始翼型的选择要包括升阻比较高与失速性能较好的翼型,还要有气动性能较差与形状不规则的翼型,用于提高翼型搜索空间的大小与设计的新颖性。翼型的加权、求和与归一化,是通过改变原始翼型的权重生成新的翼型。其中,允许单个翼型的权重为负数创建一个广泛的设计搜索空间,但任何权重的绝对值应小于1,以确保最终翼型的可用性。

根据翼型拟合的流程,通过MATLAB软件,控制翼型拟合中不同原始翼型所占的权重,来建立新翼型的模型。

1.3 气动优化平台的搭建

Z字形无人机的优化流程如图3所示,采用Isight计算机辅助优化平台,其集成了MATLAB、流场建模工具SCDM、网格划分和仿真软件Fluent多种软件,并运用遗传算法探寻设计空间内的最优方案,搭建起整机气动优化平台,实现了无人机的自动优化[8]。

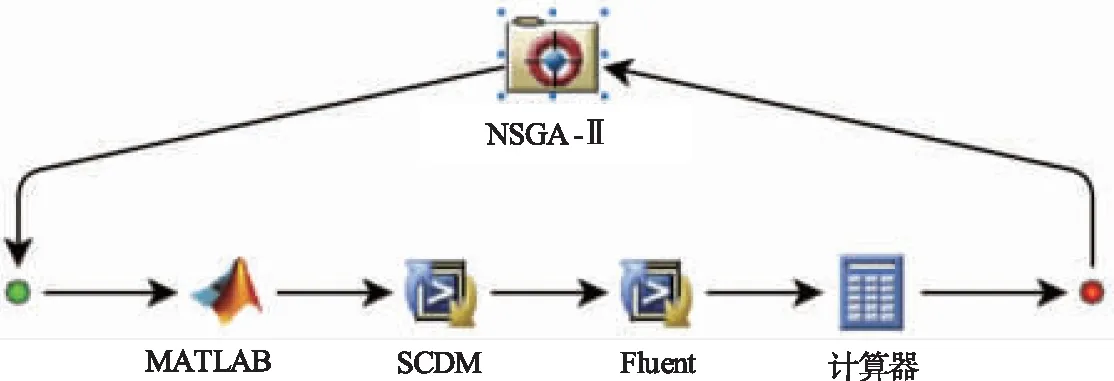
图3 无人机优化流程Fig.3 UAV optimization process

具体的气动优化流程步骤如下:

1) 使用MATLAB软件生成拟合后的翼型,通过控制不同原始翼型所占的权重生成新的翼型;

2) 使用SCDM软件对拟合后的翼型进行流场建模,生成带外流场的整机模型;

3) 使用Fluent对整机模型进行网格划分和流场计算,输出无人机的俯仰力矩和滚转力矩;

4) 使用优化算法对输出的力矩进行监测,并控制输入时不同翼型所占的权重。

计算机辅助优化平台通过组件添加的方式集成MATLAB软件,通过批处理文件控制流场建模工具SCDM与仿真软件Fluent的运行。平台自带的算法实现了输出结果的优化,解决了涉及大量重复性工作的问题。

2 优化设计方法

2.1 特殊翼型处理

针对建立翼型模型的过程中出现的翼型上下表面相交叉问题,首先对交叉点后的翼型曲线进行处理,使翼型上下表面的曲线进行交换。然后使用Hicks-Henne型函数对交叉点附近的坐标点进行正向扰动,消除机翼上下表面的交叉点,生成新翼型,增大翼型的设计空间,解决部分翼型被提前淘汰的问题,进一步提高翼型优化搜索空间。

Hicks-Henne型函数扰动的原理是对基准翼型的表面进行“鼓包”,生成新的翼型。新翼型上的坐标可表示为基准翼型坐标和扰动的线性组合[9]。翼型上下表面的表达式为

(1)

(2)

式中:yup为优化翼型上表面纵坐标;you为原始翼型的上表面纵坐标;ylow为优化翼型下表面纵坐标;yol为原始翼型的下表面纵坐标;k为控制翼型厚度分布与弯度分布关键点变量的个数;ck为控制翼型厚度分布与弯度分布关键点变量的系数;fk(x)为Hicks-Henne型函数。

(3)

7阶的Hicks-Henne型函数如图4所示,通过观察可以看出其对基准翼型的影响平滑均衡,对扰动位置的翼型后缘附近型线扰动较小,符合翼型扰动的初衷。

图4 7阶Hicks-Henne型函数Fig.4 7-order Hicks-Henne type function

2.2 数值计算

流场分析选用计算流体动力学(CFD)方法,该方法精度较高,测试成本较低[10-11]。流场分析的控制方程包括动量方程、连续性方程和能量方程,因其整体马赫数小于0.3,认定能量方程和动量方程不存在耦合关系,且密度基本保持不变[12-13]。将湍流流动中的瞬时量分解为平均量和脉动量后[14],得到的连续性方程和动量方程分别如下所示:

(4)

(5)

式中:u为流体速度;x为空间坐标;p为压力;ρ为流体密度;t为时间;i,j表示物理量某方向的分量。

上述方程中存在多个未知数,且数值计算对未知数的精度和可靠性要求较高,因此采用双精度的SSTK-ω[15]模型来解决方程封闭性的问题。

为了提高精度,二维翼型边界层网格通常需要满足一些条件,例如y+值小于1、层数大于30、增长率小于1.05等。然而,对于三维整机网格划分而言,采用以上边界层网格设置将导致计算量的激增,从而显著增加整机优化所需的时间。同时,随着有限元技术的发展,边界层网格对小型无人机仿真精度的影响已经被弱化。因此,本文在适当降低对边界层的要求的基础上,采用了壁面附近的第1层网格的y+值小于3的设置。具体的仿真设置如表2所示。

表2 数值计算设置Tab.2 Numerical calculation settings

网格划分时对机翼的前缘、后缘、连接机身处和对飞机周围的流场进行加密,特别是尾部流场进行体网格的加密,并选择1 380万、2 512万、4 235万的3种网格数量进行分析。在无人机平飞、周围环境无风、自身速度为25 m/s的情况下,气动力的计算结果如表3所示。

表3 气动力的计算结果Tab.3 Aerodynamic calculation results

由表3可知,当网格数量为2 512万和4 235万时,整机的升力与阻力误差小于0.3%,滚转力矩、偏航力矩与俯仰力矩的误差均小于3%。通过对不同网格数量结果进行对比,验证了降低边界层做法的可行性。因此采用网格数量为2 512万作为后续的计算,其流场区域体网格如图5所示。

图5 流场区域体网格Fig.5 Flow field grid

为了验证数值计算方法的可靠性,用上述方法对E387翼型进行了数值模拟,并将仿真数据与在雷诺数为20万条件下获得的实验数据进行了对比[16],结果如图6所示。由图6可知,0°迎角附近,翼型的升力和阻力偏差均相对较小,验证了该数值模拟方法的可靠性。

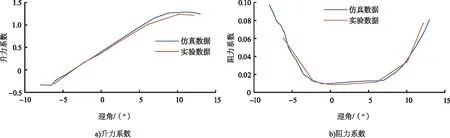
图6 仿真数据和实验数据对比Fig.6 Comparison between simulation data and experimental data

2.3 优化搜索算法的选择

优化搜索算法的目的是以更快的速度、更高的效率寻找到最优的方案。基于代理模型的寻优算法,虽然提高了优化效率,但是降低了计算结果的精确度[17-19]。局部寻优算法,优化速度快,但处理多峰问题的能力差[20-21]。全局优化搜索算法在处理多峰问题时能力较强,精度较高[22]。其中,非支配排序遗传算法是全局优化搜索算法中的一种。它的非支配排序降低计算的复杂程度,拥挤度计算解决了需人为指定共享参数的问题,精英策略提高了优化结果的精度。因此,选择非支配排序遗传算法对整机模型的滚转力矩与偏航力矩等多个目标进行优化。

图7所示为遗传算法的优化流程,其工作原理是对父代种群进行交叉、变异生成子代种群,合并父代种群中的精英种群和子代种群,对合并后的种群进行非支配排序、拥挤度计算和竞争选择生成新的父代种群,直至结果收敛时结束循环。

图7 遗传算法优化流程Fig.7 Genetic algorithm optimization process

3 优化结果与分析

3.1 算例设置

由于Z字形折叠无人机的的特殊性,在平飞过程中存在滚转力矩和偏航力矩。为此,提出保持前机翼的翼型不变,对后机翼进行优化设计的方法。通过调整后机翼的升力和阻力,使无人机的滚转力矩和偏航力矩趋于零。

在无人机平飞且自身速度25 m/s的条件下,对后机翼进行了优化。经过600次迭代,滚转力矩和偏航力矩基本满足要求。在优化后的翼型中,14个原始翼型所占的权重如表4所示。

表4 原始翼型所占权重Tab.4 Weight of original airfoil

3.2 翼型结果分析

翼型优化前后的几何轮廓对比结果如图8所示,横坐标为翼型几何轮廓横坐标X与弦长C的比值,纵坐标为翼型几何轮廓纵坐标Y与弦长C的比值。图中的原始翼型的最大厚度为弦长的11.71%,最大弯度为弦长的3.43%,分别在弦线28.0%与42%的位置。优化翼型的最大厚度为弦长的9.41%,最大弯度为弦长的3.16%,分别在弦线24.0%与60%的位置。相比于原始翼型,优化后的翼型最大厚度减小了19.7%,对应位置前移了17.9%;最大弯度减小了7.9%,对应位置后移了42.9%。优化翼型的上表面厚度大幅减小,降低了翼型的气动阻力,中部至尾缘的翼型弯度明显增大,提高了翼型的升力。

图8 翼型几何轮廓Fig.8 Geometric profile of airfoil

通过对翼型几何轮廓进行气动分析,得到了原始翼型和优化翼型的压力云图和速度云图,如图9和图10所示。相比于原始翼型,优化翼型的最大压力减小4.9%,最小压力增大22.9%,前缘附近的红色高压区域减小,上翼面的蓝色低压区域明显增多,最大速度降低3.2%,翼型前缘附近的绿色低速区域减小。优化翼型表面最大压力的减小,降低了无人机蒙皮材料所承受的最大载荷,减少了损坏的风险,从而延长了其使用寿命;翼型表面压力均匀分布,降低了维持气流流线型的难度,提高了无人机的稳定性和可控性;前缘附近气流速度增大,增加了上下表面的压力差,提高了无人机的升力。

图9 翼型优化前后的压力云图Fig.9 Pressure nephogram of airfoil before and after optimization

图10 优化前后的翼型速度云图Fig.10 Velocity nephogram of airfoil before and after optimization

原始翼型和优化翼型的压力系数如图11所示,翼型轮廓弧线位置横坐标与弦长的比值为0～0.1时,翼型上表面的压力大,下表面的压力小,升力为负值;横坐标为0.1～0.95时,与之相反,升力为正值。相比于原始翼型,当优化翼型在横坐标为0～0.1时负升力降低,0.1～0.5时升力减小,0.5～0.95时升力增大。优化翼型总体升力的增大,提高了无人机的爬升率和承载能力。

图11 压力系数变化情况Fig.11 Variation of pressure coefficient

3.3 机翼和整机气动结果分析

优化机翼与原始机翼在速度为25 m/s时的气动数据如表5所示。与原始机翼相比,优化后的机翼升力、阻力与升阻比等都得到了明显的提升,其中,升力提高了5.82%,阻力降低了23.75%,升阻比提高32.29%。与基于Hicks-Henne型函数扰动的翼型传统优化方法的优化结果[23]相比,本文在使用Isight优化平台搭建的过程中,采用原始翼型拟合与Hicks-Henne型函数扰动的策略,增加了翼型优化的搜索空间,机翼的升阻比进一步提高了14.51%。

表5 后机翼优化前后的气动数据Tab.5 Aerodynamic data before and after rear wing optimization

搭建整机三维优化平台,实现以滚转力矩与偏航力矩为目标函数的优化研究。优化前后整机的滚转力矩和偏航力矩如图12所示。优化前的滚转倾向和偏航倾向与速度、迎角、偏航角均呈线性相关,其中滚转力矩随速度、迎角、偏航角的增加而增大,偏航力矩随速度、迎角、偏航角增大而减小,正滚转力矩数值导致无人机向左侧滚转,负偏航力矩数值导致无人机向右侧偏航;优化后无人机在速度25 m/s附近、俯仰角为零、侧滑角为零时,滚转力矩和偏航力矩均趋近于零,解决了无人机滚转和偏航问题,提高了无人机的稳定性。

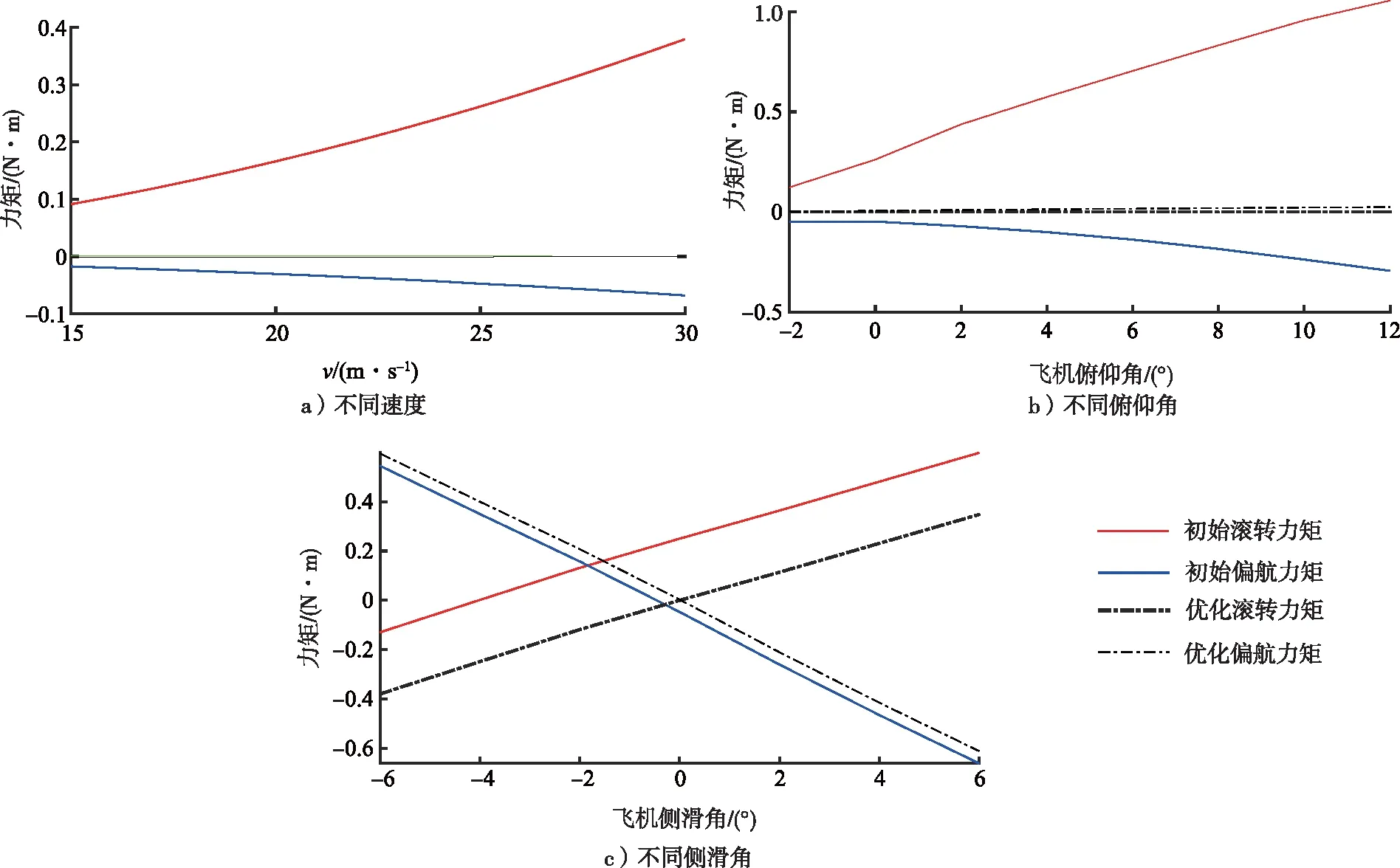
图12 飞机的滚转力矩和偏航力矩Fig.12 Rolling moment and yaw moment of aircraft

4 结 语

提出了一种基于混合翼型参数化的整机多目标优化方法,以非支配排序遗传算法(NSGA-Ⅱ)为核心与混合翼型参数化、SCDM流场建模、Fluent Meshing网格划分以及Fluent Solution流场计算相结合,建立优化模型,进而开发出基于Isight平台的自动优化流程,完成了Z字形无人机的气动优化,主要结论如下。

1)采用原始翼型拟合与特殊翼型扰动处理相结合的策略生成新翼型,增加了翼型优化的搜索空间。相比于原始翼型,优化翼型的最大厚度减小,中部至尾缘的弯度增加,具有升力高、阻力低、稳定性好、可操纵性强与使用寿命长等优点。相比于传统的基于Hicks-Henne型函数扰动的策略,升阻比提高了14.51%。

2)以消除无人机的力矩作为优化目标,搭建了气动优化的三维自动化平台。通过整机优化,机翼的升力提高了5.82%,阻力降低了23.75%,升阻比提高了32.29%;整机在速度为15～30 m/s时,滚转力矩和偏航力矩趋近于零。三维整机优化平台相比于传统翼型优化平台,更适合有限翼展的飞机,特别是小型无人机的翼型优化。

目前Z字型无人机的气动优化仍有改进空间,本文采用的优化方法,输入变量较多且模型较为复杂,导致优化速度缓慢。未来将通过引入代理模型或强化学习等手段来提高气动优化的速度,并利用Isight平台对整机进行多点、多目标优化,保证计算的准确性。