梯形渠道衬砌冻胀破坏模型研究

石玮薇

(新疆建源工程有限公司，新疆 乌鲁木齐 830000)

0 引言

在我国，冻土区面积约占总国土面积的53%，其中大部分冻土区分布在新疆维吾尔自治区，该地区冬季较长，且寒冷干旱，季节性冻土较多，昼夜温差极大，当地最高温度处于0℃以下的时间最长持续了130d。因为当地水资源分布不均匀且降雨较少，为了保证城市居民、农业灌溉、工业生产等活动的用水需求，在当地建造了较多水库，同时建设了大量引水渠道来对水资源进行调配，尤其是西北地区大部分农田灌溉用水都是来自于引水渠道[1-3]。为了减小输水过程中的损耗，避免水的渗漏，常常将混凝土衬砌布设在输水渠道的渠底与渠坡，以此来增加输水效率。但渠道使用时间过久后，一直受到水力冲刷、冻融交替等外部荷载的作用，难免会导致渠道接缝部位和衬砌发生破裂从而出现渗漏，众多学者对此也进行了研究[4-5]。肖旻[6]对新疆地区存在的刚性输水渠道衬砌冻胀现象进行了研究，提出了相应的防治措施。张晨等[7]人通过数值模拟的方式分析了寒区渠道衬砌结构对其破环形式和耐久性的影响，并优化了模拟参数，能够更加准确的反映出渠道衬砌冻胀特征。基于此，为了更好的掌握冻区渠道坡板与底板的受力情况和冻胀位移，结合地基梁弹性理论建立了渠道坡板与底板剪力、弯矩和冻胀变形计算模型，并将试验结果和模型计算值进行了验证。

1 基本假定和约束

将典型的梯形混凝土衬砌渠道作为分析对象，可根据弹性地基梁理论把衬砌板看成梁，h、b和l分别为梁的高、宽和长。利用弹簧构件来完成地基和梁之间的相互作用，梁各部位的冻胀力只由对应部位的弹簧变形(冻胀变形)来决定。根据当前的工程经验与相关学者研究成果，给出下列约定和假设：①渠道衬砌横向长度远远低于纵向长度，可将其力学模型简化成二维平面应变；②因为在冻结过程发展缓慢，所以可以把衬砌受力变形的过程看做准静态过程；③计算冻胀时只将冻深范围中冻土的冻结变形考虑在内，忽略超出冻结深度土体的固结变形；④衬砌变形属于线弹性范围，忽略微原体的转动，只对衬砌小变形进行考虑；⑤在土体冻胀时衬砌和土体的变形一直处于互相协调的状态，在衬砌达到极限平衡状态时发生破坏。

2 建立模型

分析衬砌板某一点的受力情况，能够得出衬砌单元的微分方程：

(1)

式中，E—衬砌弹性模量，MPa；I—惯性矩，m4；q、τ—冻胀力(地基反力)和切向冻结力(摩阻力)，kPa；dx—微段长度；h、b—衬砌板视作梁时的厚度与宽度，mm。

由于在现实冻胀变形时，既不可能将冻胀变形完全释放出来，也不能完全约束冻胀变形，w0(x)-w(x)可表示为约束的冻胀变形，其中实际中衬砌各部位的冻胀变形为w(x)，则实际中衬砌各部位的冻胀力可用下式表示：

(2)

式中，Ef—冻土的弹性模量，MPa；b1、a1—地质与气象有关的经验参数；z—和地下水的距离，m；H—土的冻结深度，cm。

衬砌板受到冻胀力的作用会出现弯曲变形的现象，使土体和衬砌相接触的部位出现横向位移，并且因为底部衬砌的上抬作用，会使坡板衬砌出现切向位移。不过和衬砌在冻胀作用下的切向位移相比，受到弯曲变形而产生的界面横向位移几乎可以忽略。大部分地基土和梁之间的摩阻力(冻结力)是因为受到衬砌的相对切向位移而形成的。一般情况下，冻土和构筑物界面存在的冻结力和土体含水率、剪切速率、土体温度等因素有关。在极限状态下，结合界面摩尔-库仑剪切强度准则可以得到冻结力与冻胀力联合作用情况下的挠曲线微分方程，其表达式如下所示：

w(4)+αw′+βw=γe-b1z(x)

(3)

将渠底与渠坡看做简支梁，能够得出渠道底板与坡道板的边界条件如下：

(4)

根据式(4)中的边界条件能够对渠道底板与坡道板的挠曲线微分方程进行求解。

可根据下式来对渠道底板与坡道板的横截面的弯矩和剪力进行计算：

M=EIy″

(5)

Q=EIy‴

(6)

3 项目案例和验证

3.1 工程概况

吉木萨尔县总面积为8848km2，南北长和东西宽分别为168、60km。吉木萨尔县县城有G216国道、吐—乌—大高等级公路以及S303省道贯穿县境，地理位置较好，交通便利。吉木萨尔县连通工程的任务为通过新建、改造输水管道，逐步构建布局合理、功能完备、工程优化、保障有力的河库水系连通格局，使吉木萨尔县水资源统筹调配能力、供水安全保障能力、水生态环境保护能力得到明显提高，解决北庭故城爱国主义教育基地景观用水、县城区及周边乡镇绿化用水和吉木萨尔县三大油田工业用水。吉木萨尔县气象站多年平均气温7.1℃，极端最高气温和最低气温分别为41.3、-28.6℃，7月气温最高，1月或12月气温最低。一年当中月平均气温低于零度的月份长达5个月之久，一般在11月—次年3月。多年平均风速2.0m/s，多年平均最大风速15.7m/s，风向NW，最大冻土深157cm，最大积雪厚度35cm。

3.2 对比分析计算结果

选取坡板和底板宽度为1m，结合相关研究将b1、a1定为1、15，计算和分析衬砌各部位的冻胀位移。不计摩阻力情况下，上述坡板与底板衬砌变形计算值和实测数据对比结果如图1所示。从图1中能够得出，变形实测值和此次研究所提计算模型所得结果较为接近，表明此次所提渠道坡板与底板衬砌变形计算方式较为合理，计算结果比较准确。同时本文计算方法中假设渠道底板与坡板2端部位挠度为0，而实测值并不等于0，此现象和实际情况有些偏差，但两者差值不大，仍能够达到工程标准。

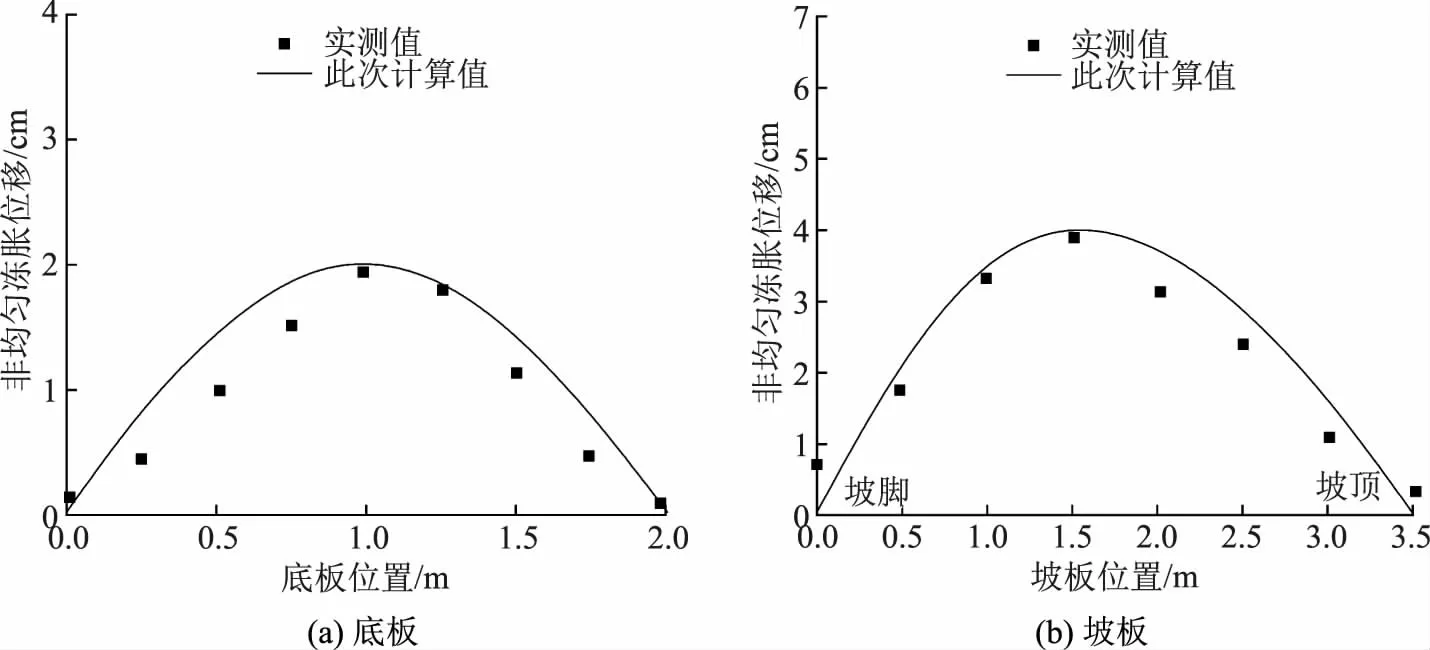
图1 实测值和计算值比较结果

渠道冻胀变形受地下水埋深影响较大，在此通过设定不同地下水位(2、1.5、1、0.5m)来计算渠道坡板和底板的内力和冻胀变形值，并且进行分析计算时忽略了界面摩阻力(冻结力)对衬砌坡板与底板的影响。底板在各地下水位埋深处的剪力、弯矩以冻胀位移如图2所示。从图2中能够得到，剪力、弯矩以及冻胀变形的最大值随着地下水埋深的增大而显著降低。底板衬砌冻胀变形最大值在地下水埋深从0.5m提高到2m时，其值从3.5cm减小到0.8cm，降低幅度达到80%，这表示可以通过控制地下水位来实现渠道的防冻胀破坏，并且在现实工程里往往会将排水井或排水暗渠设置在渠道底部，以达到减小渠道附近地下水位的目的。因为没有将渠道两边渠坡阴阳坡效应考虑在内，故渠道底板的内力与变形分布均表现为对称分布。坡板在各地下水位埋深处的剪力、弯矩以冻胀位移如图3所示。

图2 底板衬砌在各地下水埋深下计算值

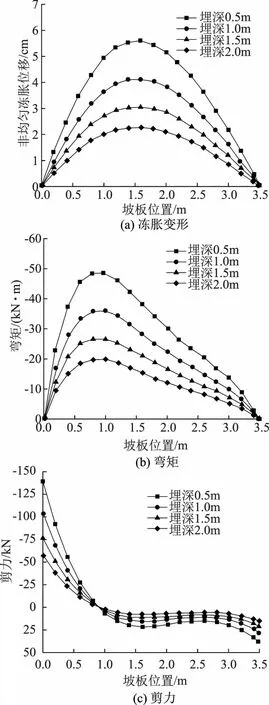
图3 坡板衬砌在各地下水埋深下计算值

从图3中能够得到，坡板剪力、弯矩以及冻胀变形的最大值和底板位置有着相同的变化趋势，均随着地下水埋深的增大而显著降低。在地下水埋深一致时，坡板不同的部位和地下水位的距离也有所不同，所以坡板各部位所受到的冻胀力是变化的，同时剪力、弯矩和冻胀位移沿坡板表现出非对称分布。在距离坡脚44%和26%坡板长度部位的冻胀位移值和弯矩值最大，这一结果与其他学者发现的梯形渠道衬砌破坏大部分出现于距离渠坡坡脚25%～45%坡板长度部位的结果相一致。

如图4所示为坡板衬砌在不同界面摩擦力因数情况下的剪力、弯矩以及冻胀变形计算值。从图4中能够发现，坡板衬砌剪力和冻胀变形受到摩擦因数的影响较小，摩擦因数对弯矩的影响略大，弯矩最大值在摩擦因数从0提高至0.7时，其值从36.4kN·m提高到40.9kN·m，提高了近12.5%。此现象是由于水平摩阻力等效于施加了一个偏心拉压荷载作用在衬砌板上，对弯矩形成了叠加。所以在对高寒地区的渠道衬砌进行设计时，仅考虑衬砌刚度时，可忽略界面冻结力对刚度的影响，当在特殊区域，重点考虑衬砌强度的情况下，不能忽略界面冻结力对刚度的影响。

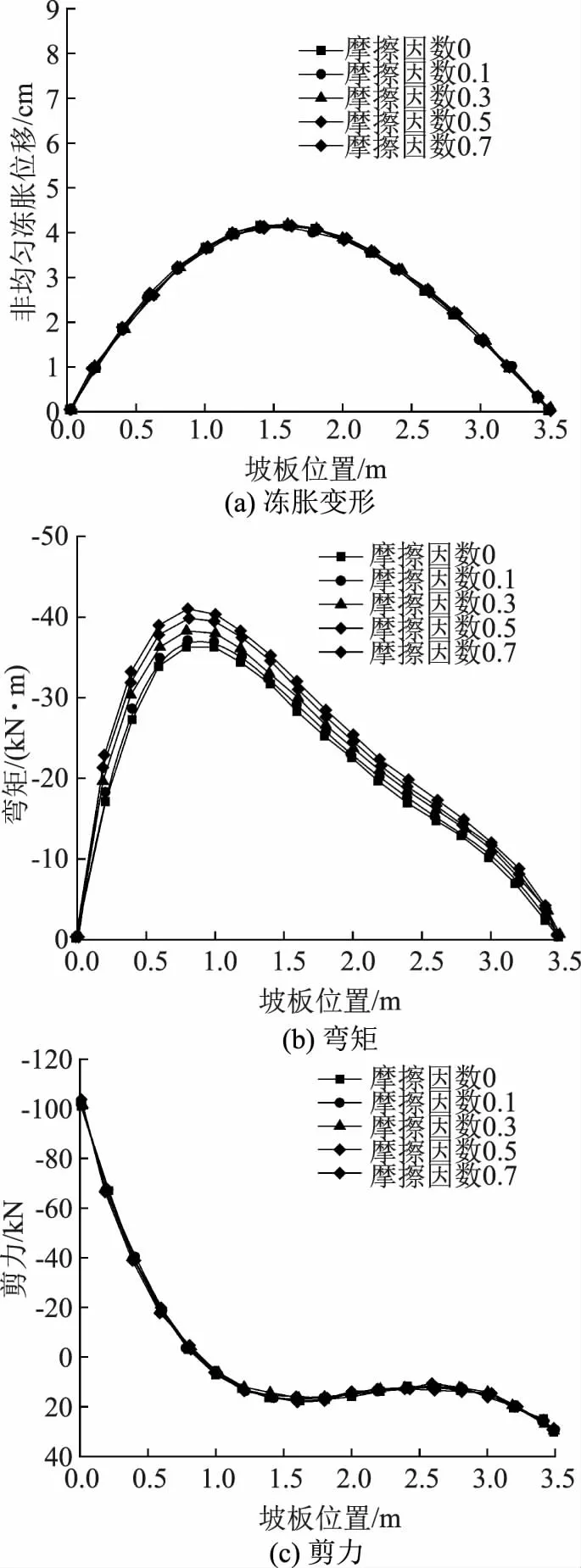
图4 坡板摩擦因数不同时的剪力、弯矩以及冻胀变形计算值

4 结论

为了更好的掌握冻区渠道坡板的受力情况和冻胀位移，此次研究以地基梁弹性理论为基础建立了考虑界面冻结力的剪力、弯矩和冻胀变形计算模型，主要得出以下结论。

(1)坡板与底板变形实测值和计算模型所得结果较为接近，表明此次所提出的渠道坡板与底板衬砌变形计算方式较为合理，计算结果比较准确；但渠道底板与坡板2端部位实测值和假定值(挠度为0)不符，两者差值不大，仍能够达到工程标准。

(2)底板衬砌冻胀变形最大值在地下水埋深从0.5m提高到2m时，其值从3.5cm减小到0.8cm，降低幅度达到80%，这表示可以通过控制地下水位来实现渠道的防冻胀破坏；在距离坡脚44%和26%坡板长度部位的冻胀位移值和弯矩值最大，这一结果与其他学者发现的梯形渠道衬砌破坏大部分出现于距离渠坡坡脚25%～45%坡板长度部位的结果相一致。

(3)坡板衬砌剪力和冻胀变形受到摩擦因数的影响较小，摩擦因数对弯矩的影响略大，在对高寒地区的渠道衬砌进行设计时，仅考虑衬砌刚度时，可忽略界面冻结力对刚度的影响，当在特殊区域，重点考虑衬砌强度的情况下，不能忽略界面冻结力对刚度的影响。