Atomistic Modeling of Lithium Materials from Deep Learning Potential with Ab Initio Accuracy

Hidi Wng,To Li,Yufn Yo,Xiofeng Liu,Weiduo Zhu,Zho Chen,Zhongjun Li,Wei Hu

a.School of Physics,Hefei University of Technology,Hefei 230091,China

b.Hefei National Laboratory for Physical Sciences at the Microscale,University of Science and Technology of China,Hefei 230026,China

Lithium has been paid great attention in recent years thanks to its significant applications for battery and lightweight alloy.Developing a potential model with high accuracy and efficiency is important for theoretical simulation of lithium materials.Here,we build a deep learning potential(DP) for elemental lithium based on a concurrent-learning scheme and DP representation of the density-functional theory (DFT) potential energy surface (PES),the DP model enables material simulations with close-to DFT accuracy but at much lower computational cost.The simulations show that basic parameters,equation of states,elasticity,defects and surface are consistent with the first principles results.More notably,the liquid radial distribution function based on our DP model is found to match well with experiment data.Our results demonstrate that the developed DP model can be used for the simulation of lithium materials.

Key words: Deep learning,Lithium,Density functional theory,Potential energy surface

I.INTRODUCTION

Lithium,the lightest metal in the periodic table,has been in the focus of research interest for several decades.As a lightweight metal,it is widely used as one of the key components in aluminium and magnesium alloy [1-3].Also it is the most important component of battery electrolytes and electrodes [4] because of its high electrode potential.In addition,the isotope6Li is a valued source material for neutron absorber in nuclear fusion [5],etc.Element lithium has 3 electrons with ground state electron configuration of 1s22s1,which is often considered as the “sample” metal because their electronic properties are well described by the nearly free-electron model at ambient conditions.However,many experimental and theoretical efforts show that this material exhibits unexpectedly complex behaviors and novel properties deviating from the nearly free-electron model.For example,based on particle swarm optimization algorithm [6],an unusual semiconductor phaseAba2-40 (40 atoms/cell) is predicted to be stable under compression of 70 GPa [7].In addition,thePbcaphase is proposed with a characteristic of Dirac nodal line semi-metal at 80 GPa [8].At low temperatures,remarkable changes in the nature of lithium would occur,including superconductivity [9,10],metal-to-semiconductor transitions [11],and highly complex low symmetry phases with up to 88 atoms per unit cell [12].Furthermore,quantum-nuclear and isotope effects are pondered to make a significant contribution to the free energies.Under the consideration of quantum and isotope effects,the ground state structure has been re-confirmed to be body-centered-cubic (BCC) rather than the previously reported meta-stable phase 9R [13].

Due to the high reactivity of element lithium,conducting experiments in diamond anvil cell with high pressure and temperatures are difficult [14].At the same time,the low temperature experiments for lithium are also a challenge.As a alternative way to exploit the properties of lithium under high pressure or lower temperature,ab initio-based molecular dynamics [15](AIMD) simulations are now routinely used because of its high accuracy.For instance,the role of quantum ion dynamics in the low melting temperatures [16] and the stability of BCC phase close to melting line [17] of lithium are systematically studied by previous works.Despite its widespread success,the first principles method like density functional theory [18] (DFT) has a high computational cost that typically scales with theO(3)system size,which,to some extent,hinders applications for researching the large-scale dynamic processes like phase transition,precipitation,and lithium ion migration under working conditions.

To solve computational cost problem,empirical force filed (EFF) has been developed in the past few decades,including Lennard-Jones potential [19],Stillinger-Wever potential [20],embedded-atom model potential(EAM) [21],and modified embedded-atom model potential (MEAM) [22].Especially,the EAM and MEAM potential are widely used in the MD simulation for metallic systems.For example,Vellaet al.[23] systematically compared six of the EAM-or MEAM-based potentials of Li and drew a conclusion that the second nearest-neighbor MEAM [24] was overall the most reliable potential.However,it still underestimates the vapor pressure.Later,Nicholet al.[25] provided an empirical potential to calculate the melting points and other thermodynamic quantities.Although the series of their potentials performed well,large discrepancy from experimental data are observed for lithium,with the melting temperature overestimated considerably.In 2017,Koet al.[26] presented a new second nearestneighbor MEAM potential for Li with good description of surface and martensitic phase transformation at low temperature.Recently,Dorrellet al.[27] conducted a systematic test for the potentials mentioned above and gave a conclusion that none of these two models can be used reliably to study high pressure of lithium.All potentials underestimate the critical pressure.Therefore,developing high accuracy version potential for Li is still an urgent problem.

In recent years,machine learning (ML) technique has dramatically promoted the development of PES.ML-based potential performs well asab initoPES and has efficiency comparable to that of empirical force field via fitting the DFT dataset.Representative examples of ML-based potentials include deep learning potential(DP) [28],high-dimensional neural network potential(NNP) [29],the Gaussian approximation potential(GAP) [30],spectral neighbor analysis potential(SNAP) [31],moment tensor potentials (MTP) [32],and so on.In this work,we develop a DP model for Li,which has been successfully used for complex systems,including TiO2-H2O interface [33],aluminum alloys[34],alkane combustion [35],crystal structure prediction [36,37],as well as high entropy alloy with up to 6 chemical species.The DP-model of Li is set to be reliable under the temperatures ranging from around 0 K to 900 K and the pressures ranging from 0 Gpa to 10 GPa.To test the DP model,we select some standard crystal structures and materials project (MP) [38]dataset.In this work,several common properties of crystal and liquid are discussed.Although most of those structures are not included in the training dataset,the resulted DP model can predict the properties reasonably,which are consistent with benchmark DFT and better than both EAM and MEAM models.

II.DEEP LEARNING POTENTIAL

A.Mathematical mechanism

Assume a system consisting ofNatoms and the corresponding coordinates of those atoms are {R1,...,RN}.Then the potential energy of system can be described by 3Nvariables,i.e.,E=E(R1,...,RN),where Ri ∈R3.Considering the extensive property of penitential energy,the DP framework [28] uses an atomic center scheme.In detail,the total energy of a system is the summation of atomic energies,

whereEiis thei-th atomic energy.As for atomic energy,it is represented as

where ∆E,∆Fiand ∆ Ξ are root mean square (RMS)error of energy,force,and virial,respectively.The prefactorspϵ,pf,andpξare weight of error,which will be updated during the optimization process.For more details,it can be found in Refs.[40,41].

B.Training data

A comprehensive training dataset is generated based on concurrent learning scheme,which has been implemented on DP-GEN software.As an open-source software platform,the DP-GEN implements the on-the-fly learning procedure and is capable of generating uniformly accurate deep learning based PES models in a way that minimizes human intervention and the computational cost for data generation and model training[42].The DP-GEN workflow consists of a series of iterations.For each iteration,three steps are included,i.e.,exploration,labeling,and training (seeFIG.1).In short,we firstly set a simple dataset to train a rough DP-model.Then the DP-GEN explores the chemistry and configuration based on this DP-model to gather new structures.The newly obtained structures are further labeled by DFT engine and are added to the dataset for training of next iteration.These procedures are iteratively executed until a reasonable DP model is obtained.In the following part,some details about initial dataset,exploration,labeling,and training are presented.

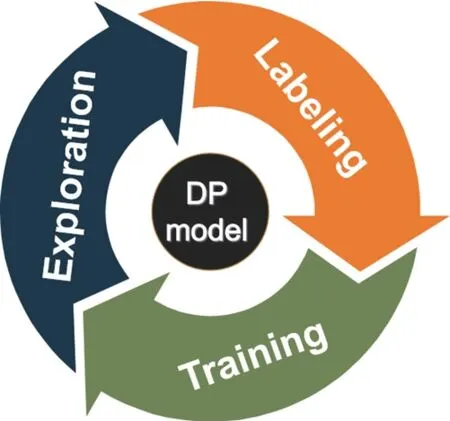
FIG.1 Basic workflow of DP-GEN based on concurrent learning scheme.

Initial datasetTo boot the DP-GEN workflow,an initial dataset set is required.For lithium system,bulk and surface data are included.As for bulk configurations,we select face-centered-cubic (FCC) (2×2×2 super-cell),hexagonal-closed-packed (HCP) (2×2×2 super-cell),body-centered-cubic (BCC) (2×2×2 supercell) structures.As for surface configurations,the FCC(100) (1×1×1 super-cell) face and HCP(100)(2×2×2 super-cell) face are included.Based on the selected crystal systems,the initial dataset is generated according to following procedures.Firstly,a random perturbation is applied to the atomic positions and cell vectors of all the initial crystalline structures,where the magnitude of perturbations on the atomic coordinates isσa=0.01 and that of the cell vector is 0.03 times the length of the cell vector.Secondly,short AIMD simulations are conducted based on perturbed structures to produce labeled data with DFT level energy,force and virial tensor.Finally,the converged DFT data are converted by dpdata [43] to DeePMD-kit supported raw data format.

ExplorationThis stage has two key components:sampler and error indicator.As for sampler,theoretically,direct MD method,MD with enhanced sampling techniques,the Markov chain Monte Carlo approach,and global optimization algorithm,etc.can be used for sampling.In this work,we use DP-based molecular dynamics (DPMD) implemented in LAMMPS package[44] to explore the configuration space.Similar to initial dataset,we also generate two types of structures:bulks and surfaces.The bulk system contains FCC,BCC,and HCP phases with random perturbation.The surface system consists of HCP(100) face and FCC(100)face.As is shown in Table S1 in Supplementary materials (SM),the exploration strategy for Li system is listed.In the first 32 iterations,only bulk FCC,BCC,andHCP phases are explored based on isothermo-isobaric(NPT) MD simulations with temperatures ranging from 50.0 K to 914.0 K and pressure from 1 bar to 5×104bar.From iterations 32 to 47,the surface systems are explored based on canonical (NVT) MD simulation.As for the last 32 iterations,the bulk system are re-explored with higher pressure,i.e.,6×104bar to 1×105bar.An indicator called model deviationϵt,which is defined as the maximal standard deviation of the atomic force predicted by the model ensemble (generally speaking,we train 4 models at the same time for the same dataset),is used to screen the candidate configurations.Here,we set lower and upper bound ofϵt ∈[0.05,0.2] eV/Å.That is to say,if theϵtof a structure is larger than 0.05 eV/Å and less than 0.2 eV/Å,this structure will enter labeling stage.

LabelingIn this stage,we use DFT engine to calculate the referenceab initioenergies,forces and virials for selected configurations.All DFT calculations are carried out with ViennaAb-initioSimulation Package(VASP) [45].The generalized gradient approximation within the Perdew-Burke-Ernzerhof [46] (PBE) functional form is used for the exchange-correlation energy.The plane wave basis sets with kinetic energy cutoff of 650 eV are used to expand the valence electron wave functions.The Brillouin zone is represented by Monkhorst-Pack [47] specialk-point mesh with resolved value of 0.1 Å-1.The convergence criterion for the energy in electronic SCF iterations and the Hellmann-Feynman force in ionic optimization step iterations are set to be 1.0×10-6eV and 1.0×10-2eV/Å,respectively.

TrainingThe DeePMD-kit package [40] with Deep-Pot-SE model is employed in the training stage.The cutoff radius of the model is set to 8.0 Å.The size of the filter and fitting networks are fixed to25×50×100 and 240×240×240,respectively.A skip connection is built (ResNet) between two neighboring fitting layers.The model is trained by the Adam stochastic gradient descent method [48] and the learning rate decreases exponentially with respect to the starting value of 0.001.The decay rate and decay step are set to 0.95 and 2000,respectively.In addition,the prefactors in the loss functions arepestart=0.02,pelimit=2,pfstart=1000,pflimit=1,pvstart=0,pvlimit=0.No virial data are included in the training process.

C.Hyper-parameters

In the DP-model,the hyper-parameters include size of fitting net,size of embedding net,and training batch.As discussed above,in the data generation stage via DPGEN scheme,the training hyper-parameters of neuron network are fixed for fast exploring the configuration space and gathering candidate data.However,once we use the DP-GEN to obtain the dataset,these hyper-parameters need to be tested for better performance of DPmodel.We test those hyper-parameters by trial and error,validate the obtained DP-model using training and test error of energy and force as shown in Table I.Based on the test result,the final hyper-parameters of DPmodel are chosen as follows: the fitting net is 180×180×180.The embedding net is set to 25×50×100 and the training batch is 8×106.FIG.2shows the comparison of energies and the force component predicted by the optimized DP-model against the reference DFT values for training and test set.Both show excellent accuracy.Specifically,the training and test error for energy is 19 meV/atom and 21 meV/atom,respectively.As for force,the training error is 14.7 meV/Å and the test error is 15.0 meV/Å.

FIG.2 DP vs.DFT resut comparision.(a) Energy,(b) force in x direction,(c) force in y direction,and (d) force in z direction for the training data and test data.The inset displays the energy or force error distributions.

D.Data availability

To facilitate the reuse and reproduction of our results,the raw training dataset,optimized DP model and some useful post-process python scripts used in this work are published on Github (https://gitee.com/haidihfut/dpmodel_li).

III.VERIFICATION OF DP MODEL

In this section,we report a series of basic tests to confirm that the proposed DP model implements the specifications correctly.

A.Equilibrium structure and equation of state

Table II compares the lattice parameters and densities of Li configurations optimized by DFT,DP,EAM and MEAM at 0 K.Take the lattice constantaas an example,the error (δa) is defined as the following equation,

whereiis the specie index,Sis the total number ofspecies (13,namely,5 standard structures and 8 MP structures),aModelis the lattice constantapredicted by using the model method,andaDFTis the lattice constantacalculated by DFT.The errors of density and relative energy can be calculated in the same way.

TABLE II The average error of lattice parameters δa,δb,δc,density δρ and relative energy (δE) of different Li configurations calculated by DFT,DP,EAM,and MEAM.

The results show that most of the DP predicted lattice parameters and densities among MP structures and standard structures are consistent with DFT results,where the relative error is less than 3%.As for the EAM potential,most of these testing cases show large prediction error,while MEAM shows a good description of lattice parameters and densities.One case needs to be noted is that the configuration MP-604313,labeled as a high pressure experimental phase in MP database,has a relative larger error for EAM and MEAM model than DP.However,the density error of MP-604313 calculated by DP is also up to 8.1%,which indicates more Li high pressure training should be included.The full results are in the SM.Overall,the DP and MEAM both have high accuracy in describing the equilibrium crystal lattices.

At the same time,the relative energies are also listed in Table S2 in SM.The relative energyδEis computed according to the formula:

whereEcell is the unit cell energy of Li allotrope,Natoms is the number of atoms per unit cell,andEstd-FCC is the energy of standard FCC Li unit cell.It can be found that DP predictions of relative energy for all tested structures are in satisfactory consistence with the DFT results,which is important for global optimization and molecular dynamics.Although MEAM model gives a good description of lattice parameters,the errors for relative energies are much larger than DP ones,so does the EAM model.

The energy and volume relationship is around the equilibrium value (80%-120% of the equilibrium volume).The equation of states (EOS) of Li allotropes calculated by DP and DFT are all shown inFIG.3.It can be found that the DP-based EOS matches well with DFT references for most of the tested cases,except the diamond-phase and MP-604313 with a small error.The inset shows that a minor energy difference (about 2 meV/atom) between BCC and FCC phases can be correctly described by DP model,which indicates that this model can be used to simulate phase transition between BCC and FCC.The same results are shown in the inset of MP structures.These results indicate that DP model generally holds its accuracy for the EOS in this volume range.

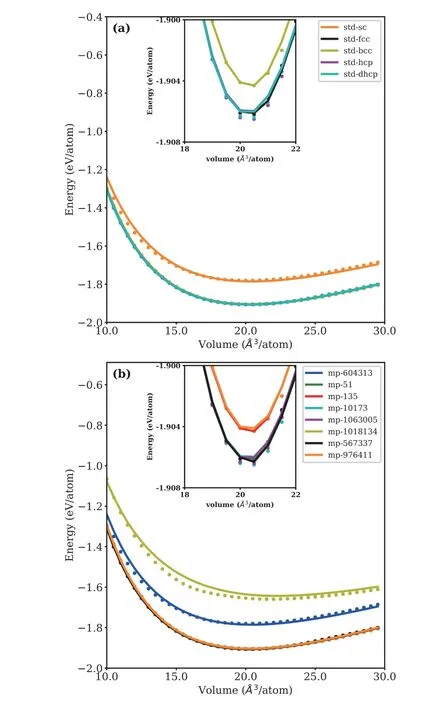
FIG.3 Equation of states of 5 standard Li configurations(a) and 8 MP structures (b).The line stands for the DP data and the dot represents the DFT data.The inset displays local magnified image.

To further examine the accuracy of the EOS predicted by different model,including DP,EAM,and MEAN,we use the root mean square error as normalized by the standard deviation of the set to show their quantitative differences.It is defined as follows:

whereEModel is the energy predicted using the model method,EDFT is the energy calculated by DFT,E¯DFT is the average of energy over the dataset,nis the index of the volume,andNis the total number of points in the dataset.The calculation based on the EOS data points shows that the average DP model error for EOS is 0.02%,which is apparently less than those of EAM(2.07%) and MEAM (1.44%) value.

B.Elasticity

The accuracy in predicting elastic properties of materials is critical for evaluating the performance of MLbased potentials.Here we calculate the elastic constants via stress-strain methodology [49],which has been implemented in Pymatgen [50].The comparison of these predicted elastic constants,elastic modulus and Poisson’s ratio along with DFT and MEAM values isprovided in Table III.Take the bulk modulusBvas an example,the error () is defined as the following equation,

TABLE III The average error of Bulk modulus ,Shear modulus ,Young’s modulus ,and Poisson’s ratio δv calculated by the DFT,DP,EAM,and MEAM models.

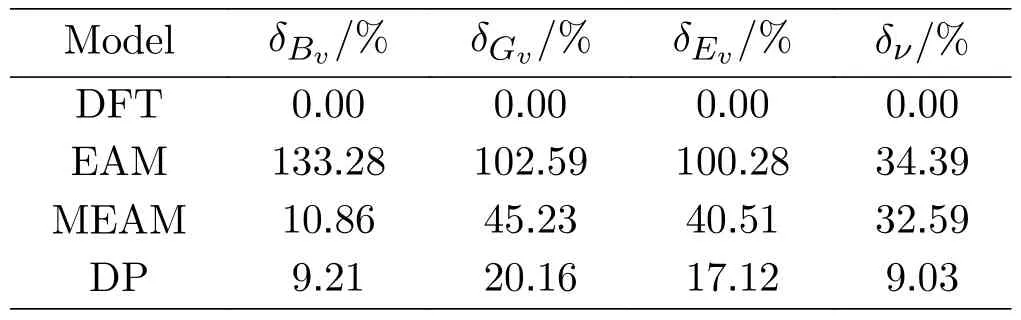
TABLE III The average error of Bulk modulus ,Shear modulus ,Young’s modulus ,and Poisson’s ratio δv calculated by the DFT,DP,EAM,and MEAM models.

It is clear that the DP model outperforms the other models in terms of accuracy,with errors ranging from 9.03% for Poisson’s ratio to 17.12% for Young’s modulus.In comparison,the errors in the EAM model are much higher,with the largest error being 133.28% for bulk modulus and the smallest being 34.39% for Poisson’s ratio.The MEAM model also shows high error,although it is lower than the EAM model.It should be noted that the large relative error for MP-604313 is common for all models.The full results are in the SM.As discussed above,one possible solution is to add more high pressure data into the training dataset.

C.Defects and surface formation energy

In this section,we investigate the point defects and surfaces of 5 standard Li configurations and 8 MP structures calculated by DP,EAM,MEAM,and DFT,respectively.In detail,the vacancy,interstitial and surface formation energy are calculated.The vacancy and interstitial formation energy (Ede) are evaluated according to the following equation [42],

whereE(Nd),Nd,andELidenote the energy of the optimized defective structure,the number of Li atom in the defective structure,and the energy per atom of the primitive cell.The single vacancy defect is randomly selected based on Li supercell.The surface formation energy (Esur) is defined by

where theEhkl,Nsur,andAsurrepresent the relaxed energy of the surface structure with Miller index (hkl),the number of Li atoms on surface,and the surface area.The results are presented inFIG.4.As shown inFIG.4(a) and (b),the calculated vacancy and interstitial formation energy based on DP is in good agreement with DFT results.Meanwhile,the results based on DP model are comparable to those predicted by MEAM and much better than those predicted by EAM.In the case of the surface configurations,the nonequivalent surfaces with Miller index values smaller than 2 are included.Obviously,we can see that the obtained surface formation upon DP and MEAM are significantly better than that of EAM,while the results of EAM deviate severely from DFT (FIG.4(c)).Our calculated results demonstrate that the developed potential provides an important step to develop accurate inter-atomic potentials for technically important Li alloy systems.

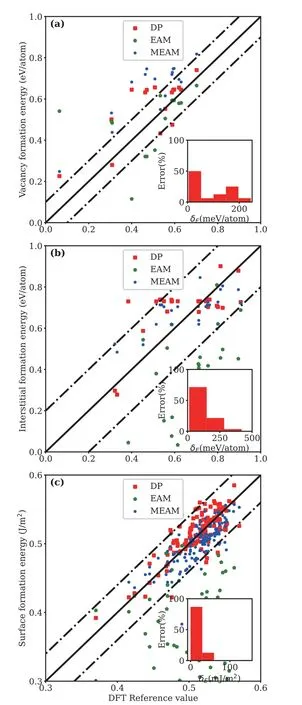
FIG.4 (a) Vacancy formation energy,the dash line shows the upper and lower limit with a shift of 0.1 eV/atom.(b) Interstitial formation energy,the dash line shows the upper and lower limit with a shift of 0.2 eV/atom.(c) Surface formation energy,the dash line shows the upper and lower limit with a shift of 0.04 J/m2.The calculated results include 5 standard Li configurations and 8 MP structures via DP,EAM,MEAM,and DFT simulation.

D.Liquid lithium

Radial distribution function (RDF) is not only an important way to study the hydrated structure of ions in solution,but also an substantial basis for the development of two types of solution theories,lattice model and radial distribution model.An path integral molecular dynamics (PIMD) [51] is carried out for liquid lithium based on the proposed DP potential.An 8×8×8 supercell with 1024 lithium atoms is simulated as the initial configuration.Firstly,the simulated system is heated fromT=0 K toT=1000 K,rapidly melts at the rate of 100 K/ps and then equilibrated as liquid state at 1000 K for 2.5 ps with a time step of 0.25 fs.In order to compare with the experimental data,the next calculation is done at 470.15 K for 150 ps equilibrium simulation with a step of 1.0 fs.As shown inFIG.5,the radial distribution functions of liquid-phase lithium using the DP potentials give the best agreement with experiment[52].The machine learning potentials essentially do as well as first-principles methods with respect to the liquid-phase radial distribution function.

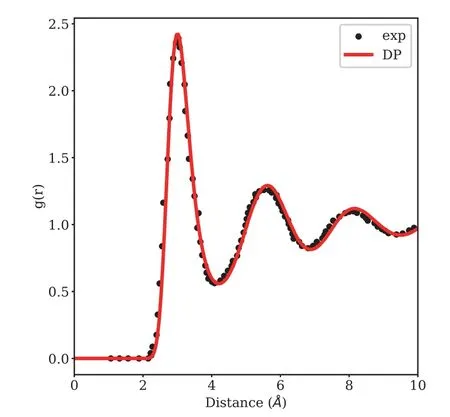
FIG.5 Comparison between the experimental and DP theoretical g(r) for liquid lithium at 470.15 K.The experimental data are labeled by black points and the theoretical ones are labeled by red line.

IV.CONCLUSION AND OUTLOOK

In this work,we develop a DP-based model for lithium via a concurrent learning scheme implemented in DP-GEN platform.Based on the proposed DP potential,we extensively test model ability to predict several properties of lithium.The properties considered include the geometric structures,equation of state,elasticity,defects,surface energy and RDF.The results show that the DP model has the same accuracy as the DFT and is much better than the empirical potential field.

It is deserved to note that the present machine learning strategy of constructing potential for pure Li can be straightforwardly applied to other metals and alloy systems.However,some drawbacks also exist for current Li DP model.For example,the performance for describing the high pressure phase still needs to be improved.And the current model cannot be directly used for complex lithium battery system.We will solve those problems in our future work.

Supplementary materials：Details of the exploration strategy;lattice parameters,density and relative energy obtained by different model;basic mechanical properties calculated by different model are shown.

V.ACKNOWLEDGMENTS

We thanks Dr.Linfeng Zhang and Dr.Yuzhi Zhang of deep modeling team for their help.This work is partly supported by the National Natural Science Foundation of China (No.22203026,No.22203025,and No.12 174080),the National Key R&D Program of China(No.2022YFA1602601),the Fundamental Research Funds for the Central Universities (JZ2022HGTA0313 and JZ2022HGQA0198),and the Anhui Provincial Natural Science Foundation (2208085QB44).The authors thanks Hefei University of Technology for the computational resources.