Minimum-Modified Debye-Hückel Theory for Size-Asymmetric Electrolyte Solutions with Moderate Concentrations
2023-11-08TiejunXiaoYunZhou
Tiejun Xiao,Yun Zhou
Guizhou Provincial Key Laboratory of Computational Nano-Material Science,Guizhou Synergetic Innovation Center of Scientific Big Data for Advanced Manufacturing Technology,Guizhou Education University,Guiyang 550018,China
A minimum-modified Debye-Hückel (DH) theory for electrolytes with size asymmetry is developed.Compared with the conventional DH theory,the minimummodified DH theory only introduces an extra surface charge density to capture the electrostatic effect of the size asymmetry of the electrolytes and hence facilitates a boundary element method for electrostatic potential calculation.This theory can distinguish the electrostatic energies and excess chemical potentials of ions with the same sizes but opposite charges,and is applied to a binary primitive electrolyte solution with moderate electrostatic coupling.Compared with the hyper-netted chain theory,the validity of this modified DH theory demonstrates significant improvement over the conventional DH theory.
Key words: Electrolyte solution,Size-asymmetry,Debye-Hückel theory,Electrostatic energy,Chemical potential
I.INTRODUCTION
The mean field theories of electrolyte solutions provide valuable insight into how the free ions response to external electric fields,and find applications in protein crystallization processes [1-3],surface tension predictions [4,5],electron transfer processes [6,7],and Coulomb criticality [8,9].
A lot of mean field theories have been developed for the restricted primitive model (RPM) electrolyte solutions,where the cations and anions have the same size and opposite charge numbers.As a hallmark of the mean field theory,the Debye-Hückel (DH) theory treats an electrolyte solution as a dielectric continuum with inverse Debye lengthkD,so that the electric potential Φ(r)of an ion in the solution satisfies a linearized Poisson-Boltzmann equation∇2Φ(r)=kD2Φ(r).The DH theory supports a boundary element method which reduces the calculation of three-dimensional electrostatic potential to the calculation of a two-dimensional problem on the molecular surface.Such a property makes the DH theory very useful in predicting the electrostatic solvation energy of biomolecules with general geometries [10,11].However,the DH theory neglects the ionic correlations and is applicable only to dilute electrolyte solutions [12].There are two ways to extend the DH theory to concentrated solutions.One way is to simply replacekDby an effective parameterκdetermined by certain physical constraints [13-15].The other way is to introduce multiple DH-like response modes rather than a single DH response mode,such as the linear modified Poisson-Boltzmann (PB) theory [16-18],the dressed ion theory [19-21],and the molecular Debye-Hückel theory [22-25].
The purpose of this study is to build an extended DH theory of size-asymmetric electrolyte solutions which is simple enough to support a boundary element method for the electrostatic potential calculations.The sizeasymmetry has significant impact on the thermodynamics and the dynamics of the electrolyte solutions[26-30].The mean field theories of size-asymmetric electrolyte solutions use either a single DH response mode[31] or a multi-DH response function [32-35].All these theories are too complicated to support the boundary element method and hence are not very efficient for the solvation of biomolecules in electrolyte solutions.
In this work,a minimum-modified DH (MMDH) theory is developed for the size-asymmetric electrolyte solutions.It is known that the size-asymmetry leads to a border zone around a solute where the charge density is nonzero even for a neutral solute [31].Such an observation implies that one should take care of the charge density induced in the border zone.In the high temperature limit,the charge density around a neutral solute reduces to a universal charge density
This paper is organized as the following: in Section II we introduce the MMDH theory for size-asymmetric electrolyte solutions,where the excess thermodynamic properties for the electrolyte solutions are also discussed;in Section III the MMDH theory is applied to electrolyte solutions with moderate electrostatic couplings;finally a brief summary is given in Section IV.
II.A MINIMUM-MODIFIED DEBYE-HÜCKEL (MMDH)THEORY FOR SIZE-ASYMMETRIC ELECTROLYTE SOLUTIONS
A.Model description of size-asymmetric electrolyte solutions
We use the binary size-asymmetric primitive model of electrolyte solutions as an illustrative model to build the MMDH theory.An ion is modeled as a charged hard sphere immersed in a dielectric background with dielectric constantϵs.A tagged ion ‘‘i’’ is characterized by a hard sphere diameterσiand a point chargeqi.Denote the elemental charge ase0,the solute charge number iszi=qi/e0.The diameters of ions are additive so that the radius of contact between an ion ‘‘i” and an ion ‘‘j”isσij=(σi+σj)/2.The total particle number density isns,the reduced inverse temperature isβ=1/(kBT)withkB being the Boltzmann constant andTbeing the temperature.The solvent ions are denoted as species 1 and 2.As we focus on the size asymmetry,we assume species 1 and 2 have the same absolute chargeq1=-q2≡qs.The particle number density of speciesiisn1=n2=ns/2.Furthermore,we assumeσ1>σ2without loss of generality.
B.A minimum-modified Debye-Hückel theory
In order to build the MMDH theory,we consider the electric potential Φ(r) of a solute which is tagged by‘‘o’’.The solute charge and diameter are denoted asQandσo.The electric potential Φ(r) satisfies the Poisson equation [36]
It is easy to check that the charge density(r)≡q2n2in the border zone resulting from the size-asymmetry and leads to a cumulate charge
then we have the following MMDH theory
Compared to the DH theory,the MMDH theory introduces an extra surface charge densityσeon the spherical molecular surfacer=b.A schematic plot of the MMDH model is shown inFIG.1.Eq.(2) is the main working equation for the MMDH theory.It is also noted that the MMDH theory coincides with a limit case of the molecular DH theory by Song and Xiao [35],i.e.,when only a single DH-like response mode is used in the molecular DH theory and the electrolyte concentration is low,the response equations (5) and (6) in Ref.[35] reduce to Eq.(2) in this work.

FIG.1 A schematic plot for the MMDH model of a spherical ion with point charge Q and radius b,where σe is a surface charge density due to size asymmetry of the electrolyte solution,kD is the inverse Debye length,Φ (r) is the electric potential.The response equation for Φ(r) is valid in the region r>b.
According to Eq.(2),the mean electric potentialΦ(r)reads
whereQc=4πσeb2is the cumulate charge caused by the asymmetric hard sphere interaction and the induced electric potentialψis defined as
As long as the mean electric potential Φ(r) is determined,one can calculate the electrostatic contribution to its excess thermodynamic properties.With the induced electric potentialψat the center of the ionogiven by,the excess internal energyuefor the solute ‘‘o’’ is evaluated as [22]
Denoteµeas the electrostatic contribution to the excess chemical potential andψ(λQ) as the induced electric potential of a solute with chargeλQ.µecan be evaluated from the Kirkwood charging process that reads
The total excess chemical potentialµexreads
where the cavity formation energyµcavcan be evaluated from the scaled particle theory [37] or the morphologic thermodynamic theory [38,39].Now it is easy to see thatueorµexare different for ions with the same diameter but opposite charge numbers,so the MMDH theory can distinguish the electrostatic energies of cations and anions.Whenσeis neglected,the MMDH theory reduces to the DH theory,such that
The induced charge densityρind(r) can also be evaluated analytically as long as the electric potential is determined.Forr≥b,
Using the analytical form of the induced charge density,one can evaluate the dielectric response functionχ(k)≡1-ϵs/ϵl(k),whereϵl(k) is the longitudinal dielectric function of the electrolyte solution.It is known that,withSzz(k) being the static charge structure factor [40],
andhij(k) is the Fourier transform of the total correlation functionhij(r)≡gij(r)-1.There are other physical constraints on the induced charge density,such as the Stilinger-Lovett(SL) second moment condition which equals toχ(k=0)=1 [41].It is known that the SL second moment condition is violated by the DH theory of RPM electrolyte solutions [13,14].After some calculations,it is found that MMDH theory leads to
so the SL second moment condition is also violated by the MMDH theory.In order to keep the SL second moment condition in size-asymmetric electrolyte solutions,one may replacekDin the MMDH theory by a tunable parameterκfollowing Attard’s treatment for RPM electrolyte solutions [13,14].However,such a modification is out of the scope of this study and will not be discussed herein.As one can see from the next section,the MMDH theory leads to satisfactory thermodynamic properties of the solution even though the SL condition is violated.This observation implies that the thermodynamic properties are integrated quantities which are not very sensitive to the detailed structures.
Here are some notes about the MMDH theory.(i)The main difference between the MMDH and the DH theory is the presence of the surface charge densityσe.Note thatσeis independent of the ion radius.One can easily apply this surface charge density to complex molecules.In the case of vanishing size differenceσ1=σ2,one find thatσe=0 and the MMDH theory reduces to the DH theory.(ii) The MMDH theory has the same functional form as the conventional DH theory and the charge densityσe resides only on the molecular surface,so the boundary element methods [42] can also be applied to the electrostatic problem defined by the MMDH theory.It is easy to extend the MMDH theory to solutes beyond spherical geometry by replacing the spherical surface in Eq.(2) with a specific molecular surface.To this end,the MMDH theory leads to a procedure that is easily applied to the solvation of biomolecules in size-asymmetric electrolyte solutions.
III.APPLICATIONS TO ELECTROLYTE SOLUTIONS
To validate the MMDH theory,we apply the MMDH theory to electrolytes with moderate electrostatic couplings.We compare our theory against the hyper-netted chain (HNC) approximation of electrolyte solutions,for which the excess internal energyβue and the excess chemical potentialβµex are known.We will show that the MMDH theory are capable of predicting the main features of the ionic thermodynamic properties.
The HNC theory is known to yield very accurate thermodynamic properties of primitive electrolytes in both the solution region and the molten salt region,where the electrostatic energy difference between the HNC theory and Monte Carlo simulation is typically 1%-2% [43-45].In our method the excess internal energyand the excess chemical potentialare evaluated according to Eq.(5) and Eq.(7),the cavity formation energyβµcavis calculated from the scaled particle theory [37].For the binary primitive electrolyte solution,all parameters used are in the dimensionless form.The parameters used for the binary electrolyte solvent areqs=1,ϵs=1,β=1,σ1=1.Note that the Debye parameteris a simple function of the total particle number densityns,we take the Debye parameterkDas a control parameter.The diameterσ2of the smaller ion is used as another control parameter.
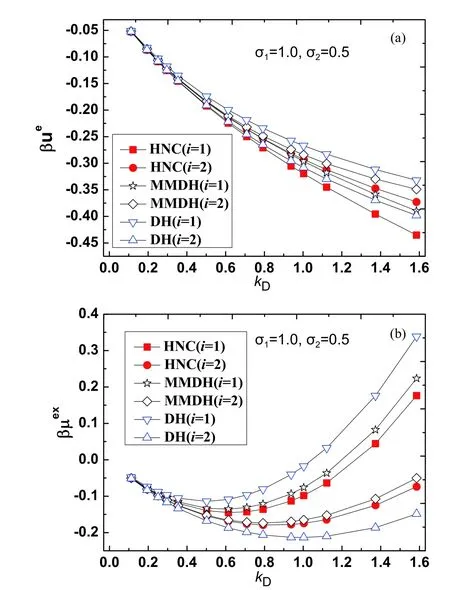
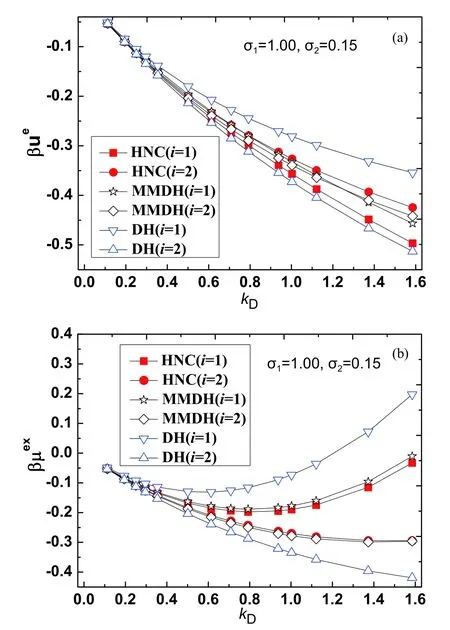
For test case I,we fixσ2=0.7 and takekDas a tunable parameter.The excess properties in the range of 0.112 FIG.2 (a)Reduced electrostatic energy βue,(b) reduced excesschemical potential βμex for ions with size σ2=0.7 and tunable kD,from the HNC theory(filled squareandcircle),the MMDH theory(hollowstar and diamond) and the DH theory (hollow triangle).The lines are guides to the eye. For test case II,we fixσ2=0.5 and takekDas a tunable parameter.The excess properties in the range of 0.112 FIG.3 (a) Reduced electrostatic energy βue,(b) reduced excess chemical potential βμex for ions with size σ2=0.5 and tunable kD,from the HNC theory (filled square and circle),the MMDH theory (hollow star and diamond)and the DH theory (hollow triangle).The lines are guides to the eye. For test case III,we fixσ2=0.25 and takekDas a tunable parameter.The excess properties in the range of 0.112 FIG.4 (a) Reduced electrostatic energy βue,(b) reduced excess chemical potential βμex for ions with size σ2=0.25 and tunable kD,from the HNC theory (filled square and circle),the MMDH theory (hollow star and diamond) and the DH theory (hollow triangle).The lines are guides to the eye. For test case IV,we fixσ2=0.15 and takekDas a tunable parameter.The excess properties in the range of 0.112 FIG.5 (a) Reduced electrostatic energy βue,(b) reduced excess chemical potential βμex for ions with size σ2=0.15 and tunable kD,from the HNC theory (filled square and circle),the MMDH theory (hollow star and diamond) and the DH theory (hollow triangle).The lines are guides to the eye. For the parameters considered,the MMDH theory is in reasonable good agreements with the HNC theory,where the energy differences are less than 11% for larger ions and less than 6% for smaller ions.The DH theory is less satisfactory,where the energy differences are as large as 29% for larger ions and 21% for smaller ions in certain conditions.In these cases,the HNC theory and MMDH theory lead to,while DH theory always leads to,so the trend for DH theory is incorrect.When the Debye parameterkDincreases,both the MMDH theory and DH theory become less accurate as expected. We have also tested the MMDH theory for binary electrolytes with different parameters,but the results are not shown for length reasons.As long as the reduced temperatureβis not large,the concentration is not high and size ratioσ2/σ1is not too small,the MMDH theory gives satisfactory results compared to the HNC theory. As the parameters in the primitive electrolyte models are dimensionless,it would be useful to relate these parameters to specific systems.Consider a 1:1 aqueous electrolyte solution with concentrationc=1.50 mol/L at temperatureT=300 K.Taking the relative dielectric constantϵr≈78.0 and a typical mean ion diameterd ≈4.00 Å,the reduced Debye length readskDd ≈1.61.So the above results imply that the MMDH theory is applicable to 1:1 electrolyte solution with concentration up to roughly 1.5 mol/L.Note that the derivation of the MMDH theory relies on the assumption of weak electrostatic coupling,one may wonder why the MMDH theory works reasonably well even for solutions with moderate concentration.This may be partly due to error cancellations,as several approximations are combined to build the MMDH theory. Note that the MMDH theory is developed for the primitive electrolytes for which ions are treated as charged hard spheres,one may wonder how to generate the MMDH theory for non-primitive electrolytes which consist of charge soft spheres.One possible hint is to use the perturbation theory to determine the effective hard sphere diameter of a soft sphere [22,25],so that charged soft spheres are mapped to charged hard spheres and the MMDH theory can be applied to non-primitive electrolytes in a straightforward way.The extension of the MMDH theory in non-primitive electrolyte solutions is underway. A minimum-modified Debye-Hückel theory for electrolyte solutions with size asymmetry is developed.Note that the size asymmetry of solvent electrolytes leads to a charge imbalanced border zone around a solute,a solute ‘‘o’’ is characterized by two types of charge sources,i.e.,a bare solute chargeQand a hard sphere contribution to the induced charge density(k)which is further approximated by a surface charge densityσe.These two kinds of charge sources are screened by the free ions in the same way,from which the electric potential as well as the electrostatic contributions to thermodynamic properties is obtained.So the MMDH theory treats an electrolyte solution as a dielectric continuum with inverse Debye lengthkDand the effect of size-asymmetry is characterized by an effective surface charge densityσe.Our model can distinguish the electrostatic energies and excess chemical potentials of solutes with positive or negative charges,and is successfully applied to electrolyte solutions with moderate concentrations. Supplementary materials:Four more figures about the excess properties of the electrolyte solution studied in the Sec.III are shown as FIG.S1(a,b) and FIG.S2(a,b),where the diameter parameter of the smaller ion is taken as σ2=0.35 or σ2=0.2. This work was supported by the National Natural Science Foundation of China (No.21863001) and a startup package from Guizhou Education University(to Tiejun Xiao);the Natural Science Foundation of department of education of Guizhou province(No.QJKY[2015]483) and a startup package from Guizhou Education University (to Yun Zhou).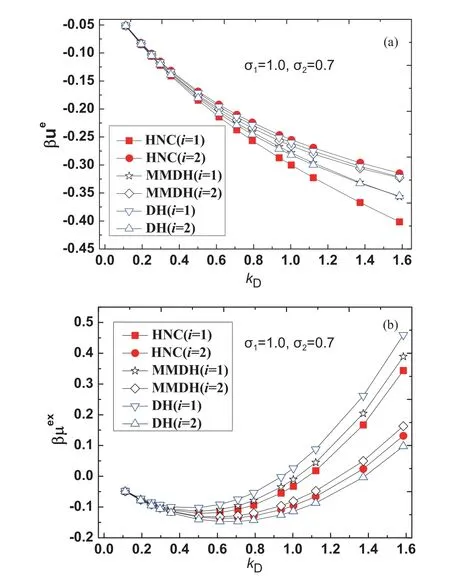

IV.CONCLUSION
V.ACKNOWLEDGMENTS
杂志排行
CHINESE JOURNAL OF CHEMICAL PHYSICS的其它文章
- Photothermal Catalytic Selective Oxidation of Isobutane to Methacrylic Acid over Keggin-Type Heteropolyacid
- Controllable Modulation of Morphology and Property of CsPbCl3 Perovskite Microcrystals by Vapor Deposition Method
- Quantum Dynamics Calculations on Isotope Effects of Hydrogen Transfer Isomerization in Formic Acid Dimer
- Design Strategy of Infrared 4-Hydroxybenzylidene-imidazolinone-Type Chromophores based on Intramolecular Charge Transfer: a Theoretical Perspective
- Third-Order Nonlinear Optical Responses of Bis(15-crown-5)-stilbenes Binding to One-or Two-Alkali Metal Cation (Li+,Na+and K+)
- On-the-Fly Nonadiabatic Dynamics of Caffeic Acid Sunscreen Compound
