Quantum Dynamics Calculations on Isotope Effects of Hydrogen Transfer Isomerization in Formic Acid Dimer
2023-11-08FengyiLiXioxiLiuXingyuYngJinweiCoWenshengBin
Fengyi Li,Xioxi Liu,Xingyu Yng,Jinwei Co,Wensheng Bin
a.Beijing National Laboratory for Molecular Sciences,Institute of Chemistry,Chinese Academy of Sciences,Beijing 100190,China
b.University of Chinese Academy of Sciences,Beijing 100049,China
We present a quantum dynamics study on the isotope effects of hydrogen transfer isomerization in the formic acid dimer,and this is achieved by multidimensional dynamics calculations with an efficient quantum mechanical theoretical scheme developed by our group,on a full-dimensional neural network ab initio potential energy surface.The ground-state and fundamental tunneling splittings for four deuterium isotopologues of formic acid dimer are considered,and the calculated results are in very good general agreement with the available experimental measurements.Strong isotope effects are revealed,the mode-specific fundamental excitation effects on the tunneling rate are evidently influenced by the deuterium substitution of H atom with the substitution on the OH bond being more effective than on the CH bond.Our studies are helpful for acquiring a better understanding of isotope effects in the double-hydrogen transfer processes.
Key words: Quantum dynamics,Isomerization,Isotope effect,Tunneling splitting,Double hydrogen transfer
I.INTRODUCTION
Hydrogen (H) transfer plays important roles in many fields [1-6],such as hydrocarbon combustions [1],transition metal-catalysts [2],and biological enzyme catalysts [3].As a result,the dynamics of H transfer has received considerable experimental and theoretical interests.In the past three decades,the single H transfer reactions and mechanisms have been well understood,and the significant contribution of the tunneling effect to the reaction kinetics and dynamics has been underscored.However,the studies of multiple H transfer process remain a great challenge for both experimentalists and theoreticians,due to the complexity in multiple H transfer [7,8].The dynamical behaviors (especial the contributions of quantum effects) in multiple H transfer processes are still elusive.
The isotope effect is usually defined as the changes in the kinetic or dynamical quantities when atoms in a molecular reactive system are substituted by their isotopes,which is greatly influenced by quantum mechanical effects such as tunneling,zero-point energy (ZPE),etc.The isotope effect [8-11] is very important in gaining a detailed understanding of the reaction dynamics and mechanisms.For example,the isotope effect can be used to determine whether the multiple H transfer occurs via a concerted mechanism or a stepwise mechanism in a series of processes,such as an enzymatic reaction [9] and the chirality switching in water tetramers on NaCl(001) [8].In a recent case,a strong quantumstate dependent isotope effect associated with the VUV photodissociation of CO was revealed experimentally,implying that such effect must be considered in the photochemical models for the understanding of the solar system and molecular clouds [10].In theoretical studies,the isotope effect is a very sensitive probe of the topographical features of the potential energy surface (PES)[12-14],and thus could be used to evaluate the accuracy or the quality of a given PES.One of the famous examples is that,in the Cl+HD reaction,exact quantum mechanical calculations on the BW2 PES [15] with van der Waals forces predict large DCl/HCl isotope effect correctly and are in excellent agreement with crossed molecular beam experiments [11],in contrast to the results using a previous PES without van der Waals forces.Besides,when the used PES is reliable,the isotope effect could also be used to test the theoretical approach if some approximations are utilized [16].
The carboxylic acid dimers have long served as the prototypes of multiple H transfer [6,17-19],among which the formic acid dimer (FAD) has been considered as the simplest benchmark system for studies of the concerted double H transfer.In FAD,the potential for the double H transfer exhibits a symmetric doublewell and a single barrier pattern along the reaction coordinate,and H transfer can occur via tunneling,leading to vibrational energy level splittings.Such splittings can be measured by the spectroscopic experiments [20,21] and calculated using various theoretical methods[22,23],and provide valuable information about the dynamics of H transfer.There have been some experimental studies on tunneling splittings of deuterated FAD.The tunneling splitting of DCOOH-HOOCD was reported in 2002 by Havenith group [24] with high-resolution infrared spectroscopic technique.In 2017,Duan group [25] measured the rotationally resolved infrared spectra of HCOOD-DOOCH,with the ground-state tunneling splitting reported as 0.00113 cm-1;they also measured the high-resolution spectra of HCOODDOOCH,and an upper limit of 0.00067 cm-1was estimated from the average linewidth for the ground-state tunneling splitting.In 2019,Liet al.[26] investigated the rotational spectra of HCOOH-HOOCD by using Fourier transform microwave spectroscopy,and obtained a precise tunneling splitting value of 331.2 MHz(0.01106 cm-1).On the other hand,the available theoretical studies on isotope effects in FAD are still limited.An accurate study on the isotope effects based upon fundamental tunneling splittings is still lacking.As for the ground-state tunneling splittings involving deuterated FAD,some quantum calculations [27-29] using the ring-polymer instanton or reduced-dimensionality approach were performed on a previous full-dimensionalab initioPES (referred to as QB) [28].However,recent calculations indicate that an improvement of the QB PES is necessary due to some deficiencies [30].
In this work,we perform multidimensional quantum dynamics (QD) calculations with an efficient QD scheme developed by us on a full-dimensional neural network (NN)ab initioPES and study the isotope effects of H transfer isomerization in FAD.
II.QUANTUM DYNAMICS METHODS
A.Process-oriented basis function customization method
The present quantum dynamics calculations are carried out using an efficient theoretical scheme deveploped by our group,which is a combination of the process-oriented basis function customization (PBFC)strategy [4,7] with several methods.The PBFC method[7,31,32] is proposed by Bian recently,and the main idea of PBFC is to customize basis functions for specific physical/chemical process,which is usually achieved by optimizing and adjusting then-dimensional (nD) effective Hamiltonian and the coordinate ranges.In the present calculations,the information about double H transfer isomerization is included into the basis function,and thenD effective potential (EP) part of the effective Hamiltonian is optimized and adjusted for the double H transfer process attracting our interest.
B.Coordinate representation and solution of matrix equation
In the present calculations,the normal coordinate representation is used,and the saddle point is chosen as the reference point of normal coordinates for the Hamiltonian.The FAD normal coordinates as well as the corresponding normal frequencies are presented in Table I.For a nonlinear system,the expression of theM-mode effective normal Hamiltonian for zero total angular momentum is [29,33]
HereQkiisanormalcoordinate,andinthe present calculations thecoordinates thatarecrucialto the process of double H transfer are taken into account;Vis theMD EP,which is obtained in accordance with the spirit of the PBFC method by minimizing the potential with all the remaining coordinates in the present calculations.Considering that the process of double H transfer mainly occurs in the plane,much larger optimized ranges are used for the coordinates of in-plane vibrational modes than those of out-of-plane modes.
The total wave function can be expanded as
whereπikj(Qkj) is the 1D discrete variable representation (DVR) basis function andNkjis the basis size.Here the 1D DVR basis function is obtained from a designed 1D effective Hamiltonian,the 1D EP part of which is customized for the process of double H transfer by using the PBFC method [29,34].
For the solution of the Hamiltonian matrix equation,the preconditioned inexact spectral transform (PIST)method [35-38] is used,in which the matrix(H-EI)-1instead of the original matrix H is employed in the Lanczos algorithm,where the shiftEis set as the energy of fundamental excitation of target mode.The PIST method can greatly reduce the needed number in Lanczos iterations,and has been extended to the polyatomic systems by our group.In addition,for better efficiency,an optimal separable basis plus Wyatt (OSBW) preconditioner [37,39-41] is combined with the PIST method,and message passing interface (MPI) is utilized to parallelize the time-consuming parts of our scheme.
III.POTENTIAL ENERGY SURFACE
Using the theoretical scheme described above,we perform multidimensional quantum dynamics calculations on a NN PES constructed by our group.The PES is constructed using a general NN fitting procedure[42-44] combined with the fundamental invariant (FI)method [45,46].The feedforward NN with two hidden layers is used,with the number of neurons in hidden layers chosen as 5 and 18,respectively.The input layer contains 1546 FIs.The “early stopping” method is used to avoid over-fitting,and the final PES is generated by averaging over six best fittings.Theab initiocalculations are performed at over 13000 symmetry-unique geometries covering various PES regions,and an accurate fit to the obtained energy points is achieved.The configurations are chosen from a previous geometry set [28]and our quasi-classical trajectory calculations.The energy calculations are carried out using the domainbased coupled cluster theory DLPNO-CCSD(T) [47,48]with the augmented correlation-consistent basis set augcc-pVnZ [49,50] (n=T).

TABLE I Formic acid dimer (FAD) normal coordinates,as well as the normal frequencies (in cm-1) on the present surface.
The quality of the fitted NN PES is measured by root mean square error (RMSE).The RMSEs for energy points below 50 and 100 kcal/mol (the energy of the lowest point inab initiocalculations is taken to be zero),are 0.061 and 0.099 kcal/mol,respectively,while the corresponding maximum errors are 1.02 and 2.10 kcal/mol,respectively.The present NN PES reaches a higher accuracy in fitting than the previous QB PES.For example,the energy-weighted RMSE(wRMSE) [28] of the QB PES,in which a weight of 0.004[(0.02+U)(0.2+U)]-1(Uis the energy of that point in Hartree) is assigned to each point of the data set,is 11 cm-1,whereas the corresponding value of the present PES is around 7.6 cm-1,or 0.0217 kcal/mol.In addition,the barrier height on the present PES is 2861 cm-1,which agrees well with ourab initioresult,and is considered to be somewhat better than the value of 2848 cm-1from the QB PES.
IV.RESULTS AND DISCUSSION
Various multidimensional QD calculations are performed with the above scheme on the full-dimensional NNab initioPES constructed by our group.The vibrational modes that are strongly coupled to the H transfer should be included,and the coupling patterns of various modes can be recognized from contour plots made using the FAD normal coordinates at the saddle point.Here,various cuts into the full-dimensional PES are obtained by plotting against specific normal coordinates with other coordinates fixed,and typical contour plots are shown inFIG.1to demonstrate the coupling patterns.In particular,we see that theQ6mode is strongly c oupled to theQ1mode,whereas the couplings betweenQ4andQ1are negligible.In addition,the couplings betweenQ17andQ1are also small,and thus the excitation ofQ17may suppress the tunneling.
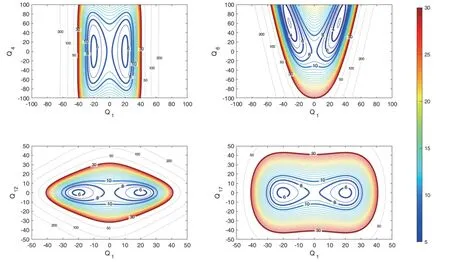
FIG.1 Selected contour plots of the surface cuts along the relevant saddle-point normal coordinates (Qi),with the other normal coordinates fixed at zero (Qi in a.u.and energies in kcal/mol).
Our analysis indicates that theQ6,Q3,Q8modes are strongly coupled to theQ1mode,and actually,a previous work [28] also shows that,theQ1,Q6,Q3,Q8modes are important in the process of H transfer.Illustrations of these normal modes are provided inFIG.2,in whichQ3denotes the intermolecular bending mode andQ8denotes the OCO bending mode.So theQ1,Q6,Q3,Q8modes need to be included in the multidimensional scheme,and our test calculations indicate that,to ob-tain converged energy levels,the basis size(NQ1=32,NQ6=13,NQ3=13,NQ8=11),denoted as (32,13,13,11) for simplicity,is necessary.The ground-state tunneling splitting for (HCOOH)2calculated with the 4D model is 0.0122 cm-1,and Table II shows that,the splitting value is lowered after deuterium substitution for H,displaying a dropping trend from DCOOH-HOOCH to HCOOD-DOOCH,which indicates strong isotope effects.

FIG.2 The typical vibrational modes of the formic acid dimer.

TABLE II Ground-state tunneling splitting for the deuterium isotopologues calculated with different models,energies in cm-1.Calculations are performed with the 1D (Q1),2D (Q1,Q6),2D (Q1,Q3),3D (Q1,Q6,Q3),and 4D(Q1,Q6,Q3,Q8)models,respectively.
We calculate the ground state tunneling splitting(∆0) for the four deuterium isotopologues (i.e.,DCOOH-HOOCH,DCOOH-HOOCD,HCOODHOOCH and HCOOD-DOOCH),and the results with different multidimensional models are presented in Table II.As can be seen,the ground-state tunneling splitting of all the four isotopologues is smaller than that of the HCOOH-HOOCH with the 4D model,which indicates that the substitution of deuterium atom for H atom will suppress the tunneling splitting.Furthermore,the ∆0 value of DCOOH-HOOCH,which is close to that of DCOOH-HOOCD,is only a little smaller than that of HCOOH-HOOCH;while the ∆0 value of HCOOD-HOOCH is about one-tenth of that of HCOOH-HOOCH and the ∆0 value of HCOODDOOCH is nearly two orders of magnitude smaller than that of HCOOH-HOOCH.
In addition,according tok=2c∆ (cis the speed of light in a vacuum),the tunneling rate (k) for H-transfer isomerization can be deduced from the tunneling splitting (∆).FIG.3shows the ratios of tunneling rates for H-transfer isomerization between the four deuterium isotopologues and FAD calculated by the present 4D scheme,from which we can see that thekD/kHratio decreases in the order of DCOOH-HOOCH>DCOOHHOOCD>HCOOD-HOOCH>HCOOD-DOOCH.On account of this,we can find that the deuterium substitution of H atom on the OH bond has a stronger suppression effect on tunneling splitting than the deuterium substitution of H atom on the CH bond.This is reasonable,since the H atom on the OH bond participates in the isomerization process with a bond making or breaking,whereas the H atom on the CH bond acts more or less like a spectator in the isomerization process.Nevertheless,in the latter case,the deuterium substitution of H atom on the CH bond will influence the whole vibrational motions of FAD in an indirect way(the reduced mass and ZPE would change),leading tokD/kHratios being slightly less than 1.

FIG.3 Ratio of tunneling rates for H-transfer isomerization between four deuterium isotopologues and the formic acid dimer calculated by the present quantum dynamics scheme with 4D model.

TABLE III Fundamental tunneling splittings for the deuterium isotopologues calculated with the 4D model.
We also find that,for all the four deuterium isotopologues,there is a trend that the isotope effect is more remarkable when more modes are included.For instance,the ratio of ∆0(DCOOH-HOOCH) and ∆0(HCOOHHOOCH) is 0.97 with the 1D model,whereas the corresponding value with the 4D model is 0.91;the ratio of∆0 (HCOOD-HOOCH) and ∆0(HCOOH-HOOCH) is 0.21 with the 1D model,whereas the corresponding value with the 4D model is 0.12,implying that the tunneling in the polyatomic molecular systems such as FAD is multidimensional and could not be described adequately by the methods based on the 1D effective potential energy.
Table II also lists the available experimental values for comparison.As shown,the calculated results are in very good general agreement with the experimental measurements.In particular,the calculated ∆0 value for DCOOH-HOOCH with 4D model is 0.01110 cm-1,which is in excellent agreement with the experimental values [26] of 0.01106 cm-1.The obtained ∆0 value of 0.00143 cm-1for HCOOD-HOOCH is also in very good agreement with the experimental value (0.00113 cm-1)of Duan group [25].In addition,the experiments by Duan group reported an upper limit (0.00067 cm-1) for the∆0value of HCOOD-DOOCH,and our value of 0.000289 cm-1is in good consistence with this limit.As for the DCOOH-HOOCD,the present result of 0.01105 cm-1is in very good agreement with an early experimental value of 0.0123 cm-1by Havenith group[24].However,considering that the reported ∆0value(0.01584 cm-1) for HCOOH-HOOCH by the same group is much larger than the most recent value of 0.01117 cm-1reported by higher resolution microwave spectroscopic experiments [26],it is more sensible to compare the ratio of ∆0(DCOOH-HOOCD) and∆0(HCOOH-HOOCH) rather than ∆0(DCOOHHOOCD) itself.The present calculations yield a value of 0.91 for this ratio,which agrees well with the value of 0.78 deduced from the experiments by Havenith group.
We also investigate the isotope effects in the tunneling splittings of vibrational excited states in deuterated FAD,and the fundamental tunneling splittings (∆i,i=3,6,8) for the four isotopologues calculated with the 4D model are summarized in Table III.As can be seen,for all the isotopologues,the obtained ∆3 values are significantly larger than the corresponding ∆0 values,indicating a remarkable mode-specific promotion effect.In particular,theQ3modes of HCOOD-DOOCH and HCOOD-HOOCH exhibit more remarkable mode-specific promotion effects than those of DCOOH-HOOCH and DCOOH-HOOCD,whereas theQ6modes of HCOOD-DOOCH and HCOOD-HOOCH lead to more evident mode-specific suppression effects than those of the other isotopologues,which implies that the modespecific suppression/promotion effects on the tunneling rate is evidently influenced by the deuterium substitution of H atom,with the substitution on the OH bond being more effective.We can also see from Table III that,for theQ3andQ8modes,the value of ∆idisplays a similar dropping trend from top to bottom,while for theQ6mode there is a different behavior.As can be seen in Table III,the ∆6 value for DCOOH-HOOCH is smaller than that for DCOOH-HOOCD,and ∆6for HCOOD-HOOCH is rather small and on the same or-der of magnitude as that for HCOOD-DOOCH.One of the possible explanations is that,the symmetry of theQ6vibrational motions (seeFIG.2) is broken in DCOOH-HOOCH and HCOOD-HOOCH,which hinders the concerted double-H transfer process and leads to remarkable suppression effects on the tunneling rate.
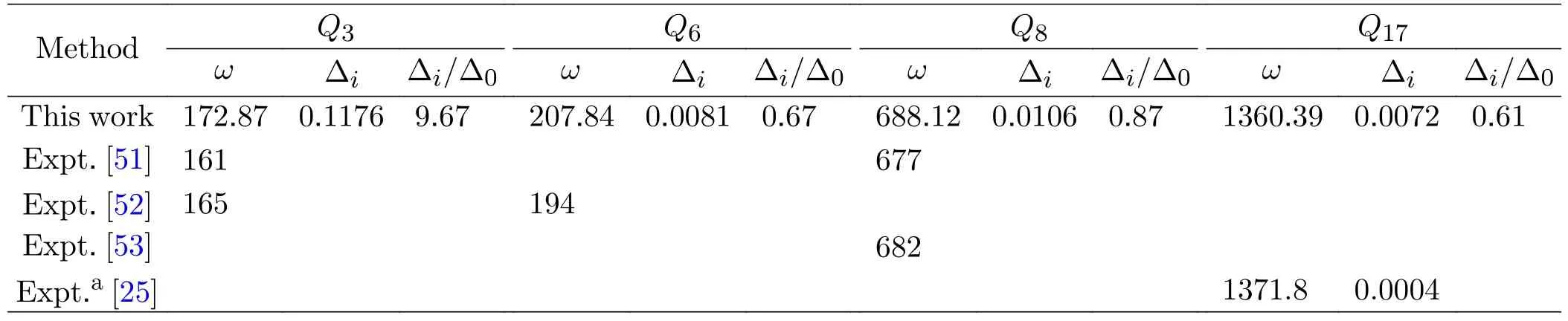
TABLE IV The frequencies (ω in cm-1) and fundamental tunneling splittings for the formic acid dimer calculated with the 4D model.
Furthermore,we calculate the frequencies and fundamental tunneling splittings for several modes of FAD with the 4D model,which is listed in Table IV.As seen,the obtained frequencies listed are in very good agreement with available experimental values,and the discrepancies between theory and experiment are<14 cm-1,which justifies the scheme used in the present calculations.We can also see from Table IV that,the effect of theQ3vibrational excitation on tunneling is significantly larger than that of the vibrational excitation of theQ6,Q8andQ17modes,which may be due to that the atom displacement of theQ3mode has effective component along the double H-transfer direction whereas the component of the atom displacement of the other three modes (Q6,Q8andQ17) are not effective (seeFIG.2).It should be mentioned that,the number of vibrational modes has been assigned according to the incensement of energy levels calculated on our surface,and the presentQ17mode (HC/OH bending) corresponds to the previousQ14mode calculated on the QB PES.The obtained fundamental tunneling splitting forQ17is 0.0072 cm-1,in reasonable agreement with the experimental value [25] by Duan group.
V.CONCLUSION
In this work,efficient multidimensional QD calculations are performed on an accurate full-dimensional NNab initioPES constructed by our group,with the PBFCPIST scheme.The ground-state and fundamental excitation tunneling splittings for four deuterium isotopologues of FAD are investigated.The obtained results are in very good general agreement with the available experimental values,with strong isotope effects being unraveled.In particular,the vibrational excitations of different modes exhibit interesting mode-specific suppression/promotion effects on the tunneling rate,and such effects are evidently influenced by the deuterium substitution of H atom,with the substitution on the OH bond being more effective.The present work also demonstrates the efficiency of our PBFC-PIST scheme.We hope that the present work will stimulate further experimental interests in isotope effects on double-H transfer.
VI.ACKNOWLEDGMENTS
This work is supported by the National Natural Science Foundation of China (No.21973098 and No.22133003),and the Beijing National Laboratory for Molecular Sciences.Jianwei Cao acknowledges the Youth Innovation Promotion Association CAS(No.2018045).
杂志排行
CHINESE JOURNAL OF CHEMICAL PHYSICS的其它文章
- Minimum-Modified Debye-Hückel Theory for Size-Asymmetric Electrolyte Solutions with Moderate Concentrations
- Controllable Modulation of Morphology and Property of CsPbCl3 Perovskite Microcrystals by Vapor Deposition Method
- Design Strategy of Infrared 4-Hydroxybenzylidene-imidazolinone-Type Chromophores based on Intramolecular Charge Transfer: a Theoretical Perspective
- Photothermal Catalytic Selective Oxidation of Isobutane to Methacrylic Acid over Keggin-Type Heteropolyacid
- Third-Order Nonlinear Optical Responses of Bis(15-crown-5)-stilbenes Binding to One-or Two-Alkali Metal Cation (Li+,Na+and K+)
- On-the-Fly Nonadiabatic Dynamics of Caffeic Acid Sunscreen Compound
