直流电机恒流制动和吊物落速动态控制方法研究
2023-11-08黄勃铭白海城姜相国
黄勃铭, 白海城, 姜相国
(1.辽宁石油化工大学 信息与控制工程学院,辽宁 抚顺 113001; 2.辽宁石油化工大学 人工智能与软件学院,辽宁 抚顺 113001)
反抗性负载的快速停车制动与位能型负载的落速控制,对提高电机拖动装置的动态运行效率和生产安全具有重要意义[1]。直流电动机由于其良好的启动和调速性能、较大的转矩以及受电磁干扰影响小等优点,在电力拖动和机器人控制系统中得到了广泛应用[1-3]。直流电机有电动和制动两种运转状态。研究电机制动的目的是使含有反抗性负载的电力拖动系统快速停车或减速。对于含有位能负载的升降机构,通过制动还可以使悬吊物获得稳定高效的落速控制。直流电机制动方式总体上分为机械制动和电气制动[4]。其中,电气制动包括能耗制动、反接制动和回馈制动。电气制动具有灵活性、易控性和寿命长等特点,因而在自动化控制领域得到了广泛应用[5]。常规能耗制动时将电枢与电源断开,并将电枢接到一个固定的制动电阻Rz上,把负载动能转化为电能并消耗在此电阻上,它既适用于反抗性负载的停车制动,又适用于位能型负载的稳速落放[6]。反接制动时需要将电源反接,同时在电枢回路中串入制动电阻Rz用于吸收负载动能,其特点是制动转矩较大,适用于频繁正反转启动和制动的运行方式。回馈制动时由位能负载带动电动机发电,电枢将轴上负载的机械功率变为电磁功率并回馈给电网,因此较为经济,但对位能负载而言难以获得较低的落放速度[7]。
上述三种电气制动方式均可用明确的机械特性方程进行描述。但是,现有制动方法均是基于某一固定制动电阻Rz基础上的,其存在的主要问题有:对反抗性负载而言,在系统停车制动过程中,随着电机转速的降低制动转矩也随之减小;由于期间无法保持恒转矩制动特性,因而难以实现制动效率的最大化;对位能型负载的落放过程,重物从静止状态到达稳定落速的时间较长,且在不改变制动系统硬件的条件下,重物只能以固定的稳定速度落放[8],难以实现变速落放的控制要求。
本文提出了一种由功率场效应管取代常规能耗制动电阻,并通过压控方式在线调节其漏极与源极之间等效阻值的他励电机新型制动方法。该方法在无须改变系统硬件的条件下采用电流和转速双闭环控制技术,并结合数字信号处理器,针对反抗性负载可实现全程恒流快速停车制动;针对位能负载,可实现对悬吊物的快速落放和落速的动态调节。该制动方法不仅能有效提高电机拖动系统的动态运行效率,还可以增强控制系统的灵活性和通用性。
1 恒流停车制动及负载落放的机械特性
恒流停车制动,是指电机拖动系统从初始制动时刻到停车的整个时间段内电枢中的制动电流IB始终保持恒定,且其值为电机在短时内所允许的最大电流IBmax[9]。本文提出的恒流制动的基本原理是用一个功率场效应管漏极与源极间的等效电阻Rds取代常规能耗制动方法中的固定电阻Rz,且Rds能够通过压控方式在线动态调节。电机的制动机械特性曲线如图1 中的Ⅱ、Ⅳ象限所示。图1 中,Ⅱ、Ⅳ象限分别反映反抗性负载的停车制动和位能负载下落时的制动特性;B-C-O实线段对应恒流制动;B-O虚线段对应常规能耗制动;O-ns-D-E实折线段对应负载的稳定落速,它具有可控性;O-E虚线段对应负载的稳定落速,它是固定不变的。若制动前电机的电动转速度是ni,因在制动的初始时刻ni保持不变,工作点由A点沿线段AB平行移动到B点,电动机进入制动状态后开始减速。对于恒流制动,转速将沿线段BC下降,期间制动转矩始终保持最大转矩TBmax。当电机转速n下降到nc(转折转速)时,制动转矩才沿线段CO线性减小,直至n为零时停车。

图1 直流电机制动机械特性曲线
nc的表达式见式(1):
式中:Ra为电枢固有电阻,Ω;Ce为电动势常数;φ为每极磁通量,Wb;IBmax为电机短时所允许的最大制动电流,A;nc等于MOS 管刚好完全导通时的电机转速,r/min。此时,因MOS 管源极与漏极之间的等效电阻Rds已经近似为零,制动电流已不再受MOS管控制,而完全取决于电枢的自身电阻Ra及其反电动势。事实上,因Ra很小,故nc较小,在整个制动过程可近似地视为由恒流段BC构成。O-ns-D-E段对应位能型负载落放时的制动机械特性,ns为期望达到的电机稳定转速。位能负载下落时带动电机从静止状态达到ns,经由过冲点D,最后转速稳定在ns。需要说明的是,电机转速的过冲是因为速度闭环调节导致的,其过冲量与过冲时间取决于调节器的控制算法,一般较小。通过以上分析,恒流制动的机械特性可表示为:
式中:T为电磁转矩,N·m;TBmax为电机所允许的最大制动转矩,N·m;TL为负载转矩,N·m;n为电机转速,r/min;CT为转矩常数;ns表示位能负载稳速下落时的电机转速或控制系统的设定落速,r/min;nc为过渡转速,r/min。
设常规能耗制动电阻为Rz,则其制动时的机械特性可表示为[10-11]:
由式(3)可见,常规能耗制动的机械特性为一经过原点的直线,转速n与电磁转矩T正相关,见图1 中的线段BE。
2 转速/电流随时间变化模型
为了深入分析恒流制动特性,图2 给出了在恒流制动过程中制动电流和制动转速随时间的变化曲线。图中,实线对应恒流制动法,虚线对应常规能耗制动法;tc表示恒流制动的转折点;to1与to2分别表示恒流制动与常规能耗制动过程的停车时刻;ts1与ts2分别表示恒流制动和常规能耗制动过程在位能负载下落情况下达到稳定落速的时刻;ni表示电机的初始转速。需要说明的是,这里的原点代表初始时刻,故各个时刻点也代表制动过程所经历的时间。

图2 恒流制动过程中制动电流和制动转速随时间的变化曲线
2.1 反抗性负载的停车制动时间
从图2 可以看出,恒流制动法的制动电流总体保持恒定,制动转速随时间总体上按线性规律下降。但是,常规能耗制动法制动电流和制动转速均随时间按指数规律下降。显然,无论是对反抗性负载的停车制动还是对位能负载的落放制动,恒流制动效率较常规能耗制动效率均有显著提升。恒流制动的根本目的是在电机短时所允许的过流条件下以最快速度使带有反抗性负载的电机停车。下面针对制动时间进行量化分析。
由于受机械惯性和功率承载能力的限制,电机的最大制动电流一般为额定电流的两倍,即IBmax=2IN,TBmax=2TL。首先考虑常规能耗制动法,将电机运动方程式T=TL+GD2/375×dn/dt(G为旋转部分的重力,D为惯性直径)代入式(3),有:
由式(3)可知,当T=TL时,n=ns,即当过渡过程结束时电机的稳定转速为:
由式(5)与式(4)可得常规能耗制动下的转速微分方程:
其中,TtM1=GD2(Ra+Rz)/(375CeCTφ2),称为机电时间常数。此一阶微分方程的解为:
由图1 中的几何关系可知,ni=-2ns。当n=0时,由式(7)可求得在常规能耗制动方式下电机从初始转速ni到停转的制动时间:
针对恒流制动方法,电机从ni到停转的制动时间to1由Otc时间段和tcto1时间段构成(见图2(b))。其中,Otc时间段内制动电流保持恒定,随着转速的降低,MOS 管的漏级与源极的等效电阻Rds在闭环压控过程中逐渐减小,直至到达tc时刻MOS 管完全导通,此时对应的转速为nc,即过渡转速,其值可表示为:nc=2TLRa/(CeCTφ2)。结合式(5)并考虑到ni=-2ns,得nc与ni的关系为:
在tcto1时间段,因MOS 管已完全开启对应的导通电阻即Rds≈0,电机只在电枢绕组自身电阻Ra的作用下进行能耗制动。由上述分析知,图2(b)中恒流制动直线段niC恰好为常规能耗制动曲线nito2在零时刻的切线。对式(7)两端求导,得:
考虑到边界条件,当t=0 时,ni=-2ns,切线niC的斜率为k=-1.50ni/TtM1。其对应的直线方程为
当n=nc时,由式(9)和式(11)可得Otc段对应的时间:
因tcto1段属常规能耗制动,由式(8)可得,tcto1=1.10TtM2,其中,TtM2=GD2Ra/(375CeCTφ2)=RaTtM1/(Ra+Rz)。结合式(12)可知,对于恒流制动方法,电机从初始转速ni到停转的总制动时间为:
对TtM1和TtM2进行归一化处理,式(13)可表示为:
通过比较式(8)和式(14),可以得出如下结论:
①当制动电阻Rz=0 时,to1=to2=1.1TtM1。此时,恒流制动与常规能耗制动时间相同,Otc时间段为0。
②Rz与Ra的差值越大,恒流制动时间to1越小于常规能耗制动时间to2。若IBmax=2IN,则Ra+Rz=UN/(2IN)(UN、IN分别为电机的额定电压和额定电流)。在通常情况下,Rz大于4Ra,此时to1小于0.75TtM1,即to1小于0.68to2。由此可见,理论上恒流制动方法可将停车制动时间至少缩短为常规能耗制动方法的68.0%,因而有效提高反抗性负载的停车制动效率。
2.2 位能负载落速动态控制
如果电动机带动位能型负载,在吊物下落过程中,电机的机械特性将位于第Ⅳ象限。从图1 的机械特性曲线可以看出,对于常规的能耗制动法,电磁转矩T将随着负载反向落放速度的增加而逐渐增加,直至T=TL时系统加速度为零,电机带动悬吊物体以n=ns的速度匀速旋转。因此,针对某一特定的制动电阻Rz,位能负载只能以一个固定的速度落放。电机拖动负载从静止到稳定转速ns的落放时间可由式(7)在ni=0的条件下求得。理论上,只有当t=∞时,n才将达到ns。但是,当t=3TtM1时,电机转速就已达到ns的95.0%。因此,常规能耗制动法的位能负载从静止状态达到稳速的落放时间近似为3TtM1。
本文通过DSP 以压控方式动态改变功率MOS管源极与漏极之间的等效电阻取代固定制动电阻Rz,在不改动硬件的条件下实现电机对位能负载的快速落放控制和稳定落速的动态调节。图2 中的to1ts1时间段对应吊物的落放过程。在该时间段内功率MOS 管完全关断,电枢回路的电流Ia和制动转矩T均为零,因而在忽略电机自身转动惯量的情况下吊物以自由落体方式下落,直至达到系统预先设定的稳定转速,MOS 管开启并产生与负载转矩TL相等的电磁制动转矩T。在忽略轴惯性时,该动态过程可以表示为:
取边界条件t=0,n=0,则当n=ns时,该方程组的解即为吊物达到稳速落放的时间:
为便于与常规能耗制动法比较,将ns=Ia(Ra+Rz)/(Ceφ)与TL=-CTφIa代入式(16)并进行归一化:
由此可见,落速动态控制法不但可以实现位能负载稳定落速的动态控制,而且可将吊物达到稳定落速的时间缩短到常规能耗制动法的33.3%,有效提高电机拖动系统的通用性和高效性。
3 恒流制动及吊物落速动态调节系统设计
3.1 硬件电路设计
图3 为他励直流电动机恒流制动及位能负载落速动态控制系统的硬件构成。系统主要由用于电流和转速反馈的两个独立的PI 调节单元、功率MOS 管Tp及信号隔离单元构成。其中,功率MOS管作为核心构成单元,其漏极与源极接入电机制动回路。两个PI 调节器的给定转速ns和给定最大制动电流IBmax均由DSP 程序设定,速度反馈量取自测速发电机TG 的输出,电流反馈量通过取样电阻RS的电压值间接获得。电流闭环用于实现反抗性负载的恒流制动,而速度闭环用于实现位能负载落放速度的控制。两个PI 调节器的输出通过模拟多路开关并经过线性光隔离放大器驱动后作用于功率MOS 管的栅极,从而实现压控电阻的功能。模拟开关的通道选择由DSP 的I/O 引脚控制。对应电机的正转和反转,测速发电机的输出电压Utg具有正负性,故需将其与一正偏置电压相加后变为单一极性的电压信号,再通过DSP 的内置AD 端口采集转速。信号隔离单元可由变压器或线性光耦放大器构成,热敏电阻Rt 用于对功率MOS 管的工作温度进行实时监测。

图3 他励直流电动机恒流制动及位能负载落速动态控制系统的硬件构成
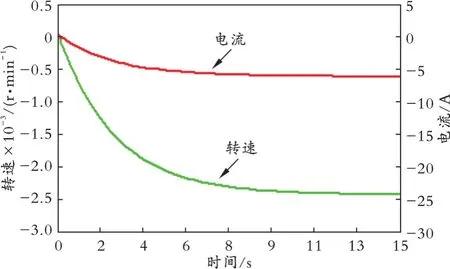
无论是恒流制动还是吊物落速动态控制均是基于功率MOS 管的压控可变电阻特性。图4 为MOS 管Rds 的压控特性。由图4 可知,当其栅极与源极电压Vgs小于门槛电压Vth时,源极与漏极的电阻Rds=∞;当Vgs大于开启电压Von时,Rds≈0;当Vth 图4 MOS 管Rds的压控特性 电机的工作状态可通过DSP 的I/O 口对开关SW 检测确定。当其闭合时,模拟多路开关选择CH3通道,此时Tp因Vgs 恒流制动的工作过程如下: ①由程序设定的IBmax经DSP 内置D/A 变换和反相器后转换为与其成比例的电压Uig=kIBmax(k为负数),而从取样电阻Rs获得的电压经反相器和光隔放大器后得到与制动电流成比例的反馈电压Uif,其值为正。图5 为PI 调节器1 和2 的电路构成,其中调节器1 的输出电压可表示为: 图5 PI 调节器1 和2 的电路构成 ②PI 调节器的输出Uo经多路开关选择和线性光隔放大后用以实现对Tp等效电阻Rds的压控调节。当实际制动电流IB小于程序设定的给定电流IBmax时,Uif<|Uig|。由于积分效应,Uo大于0 且不断增加,导致Rds不断减小,IB逐渐增大,直至IB=IBmax时Uo才趋于稳定。此时,Rds也稳定在某一确定值,电机进行恒流制动状态,对应图2 中的Otc段。 位能负载的落速控制主要是通过速度PI 调节器2、测速发电机TG 和功率MOS 管Tp的压控电阻特性实现的。其具体过程为:当DSP 检测到电机制动转速降为0 时,将模拟多路开关切换到CH2通道。此时,由程序设定的吊物稳定落速经D/A 变换器转换为与之对应的给定电压Ung。对Ung与TG 输出的与转速成正比的反馈电压Unf进行比较。由于吊物落放时电机反转,TG 输出电压Unf为负,故PI 调节器2 的输出电压可表示为: Uo经多路开关选择和隔离器放大后用以实现对Tp等效电阻Rds的压控调节。由式(19)可知,当反馈速度低于给定速度,等效于|Unf| 软件控制算法如图6 所示,它由主程序和中断服务程序构成。主程序的功能主要有:DSP 寄存器初始化;设定电机制动电流值IBmax(与Uig对应)和位能负载的稳定落速ns(与Ung对应);检测开关SW 用于判断电机是处于电动还是制动状态,并据此进行模拟多路开关的通道切换。中断服务程序用于实时检测功率MOS 管温度,以便对控制器进行过温报警和保护。 图6 软件控制算法 为了检验上述恒流制动和负载落速控制方法的有效性,采用国际公认的Multisim 仿真工具对上述理论进行了实验验证[12]。图7-10 给出了四组典型的比对实验结果,其所对应的电机参数如下:转速为9 258 r/min,轴转动惯量为0.015 kg·m2,电枢电感为0.1 mH,电枢电阻为0.2 Ω,IN=12.5 A,UN=80 V,IBmax=25 A。由图7-10 可以看出,四组实验曲线的合成波形与图2 所对应的理论分析结果一致,从而定性证明了上述电机制动理论的正确性。 图7 传统停车制动曲线 图8 恒流制动实验中转速和电流随时间的变化曲线 图9 传统负载落放制动实验中电流和转速随时间的变化曲线 图10 负载落速动态控制实验中电流和转速随时间的变化曲线 为了充分评估理论模型的准确性,有必要进一步对其进行多元化量化实验。表1 是在转动惯量为0.015 kg·m2、制动电流为额定电流2 倍的条件下,分别采用两种不同的制动方法测得的电机停车时间。其中,UN为电机额定电压,IN为电机额定电流,tB为恒流停车制动时间,tN为常规能耗停车制动时间,ηp为tB与tN之比。由表1 可以看出,ηp的最小值和最大值分别为65.0%和67.3%,与理论值66.7%吻合。经计算可知,相对误差小于2.5%。 表1 不同参数下两种电机制动方法的停车时间比较 表2 是在转动惯量为0.005、ni=0 时,分别采用两种方法测得的位能负载从静止到达稳速的落放时间。 表2 中,Is为稳定落放电流,tf为速度动态调节方法所对应的吊物由静止到达稳速的时间,tn为常规制动方法所对应的吊物由静止达到稳速95%的时间,ηd为tf与tn之比。由表2 可以看出,ηd的最小值和最大值分别为33.1%和33.7%,与理论值33.3%具有较好的一致性,经计算可知相对误差小于1.2%。 本文提出了一种由功率场效应管取代常规能耗制动电阻的直流电机恒流制动和吊物落速动态控制方法,据此建立了系统的机械特性方程,系统分析了在恒流停车制动和吊物落放过程中制动转速和制动电流随时间的变化。结果表明,恒流制动方法可将停车时间至少缩短为常规能耗制动方法的66.7%;落速动态控制法不但可以实现位能负载下落速度的连续调节,而且可将吊物达到稳定落速的时间缩短为常规能耗制动方法的33.3%。在此基础上,设计了系统的硬件电路和软件算法,证明了本文提出的恒流制动和落速动态控制技术的可实现性。通过不同参数组合情况下的多元化仿真实验,从定性和定量两种角度充分证明了本文提出的电机制动理论的正确性。该方法的实施能够有效提高直流电机拖动系统的动态工作效率,同时还有助于增强电机控制系统的通用性。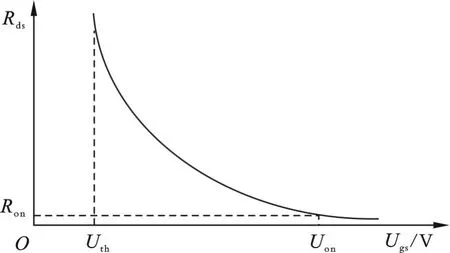
3.2 软件算法设计

4 系统仿真实验
4.1 仿真参数设置及性能比较
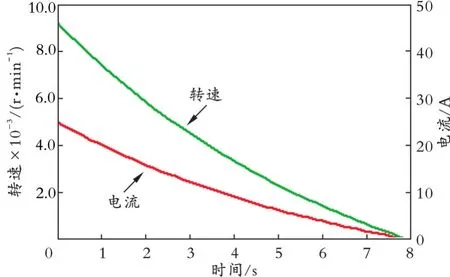
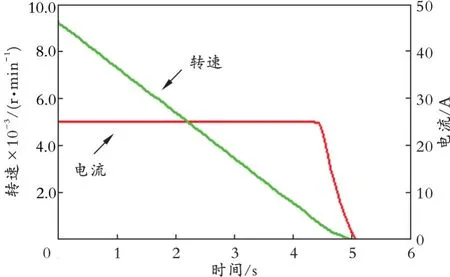

4.2 实验结果的定量分析

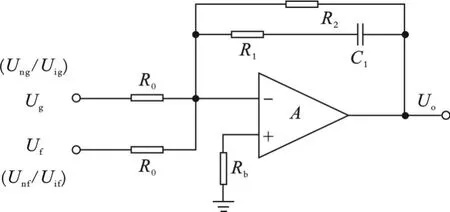
5 结 论
