基于流场特性分析的安全壳整体性密封性试验方法研究
2023-11-08娄淑雅顾济民沈东明黄晓明许国良
娄淑雅 ,顾济民,沈东明,何 锐,黄晓明,*,许国良
(1.华中科技大学能源与动力工程学院,湖北 武汉 430074;2.中广核工程有限公司核电安全监控技术与装备国家重点实验室,广东 深圳 518172)
作为核电站纵深防御原则的最后一道实体屏障,确保安全壳在任何情况下的密封性对核安全有着重要的意义[1]。整体泄漏率试验(Integrated Leakage Rate Test,ILRT)是目前监督安全壳整体密封性是否满足要求的重要手段[2-5]。整体泄漏率无法直接测量,因此整体密封性试验的原理是在设计压力下,通过连续测量安全壳内压力、温度和相对湿度,再依据理想气体状态方程计算出安全壳内空气总质量变化规律,以确定整体泄漏率[6-8]。这种气体流量计量方法又被称为pVTt 法[9]。可以看出,安全壳泄漏率测量的准确性十分依赖整体密封试验过程中测点布置和平均参数的计量方法[10,11]。
核电站安全壳内部净容积相当大,如CPR1000 安全壳内部自由空间约49 400 m³,EPR 安全壳内部自由空间约为78 000 m³。此外,安全壳内部空间因设备安装和工艺要求被分隔成若干个隔间,这些隔间布置对安全壳内气体的流动与传输有着很大的影响。因此,安全壳内部的温度分布和湿度分布是不均匀的,需要布置许多有代表性的传感器进行测量。通常,几万方的自由空间只能设置70~100 个温度传感器,每个传感器的测得值分配了一定的自由容积值Vi,Vi与安全壳总自由空间V的比值被称为该传感器的权重因子。将传感器的测量值根据权重因子进行加权平均,计算出平均温度,是安全壳整体泄漏率计算中的重要步骤[12-14]。
文献[15-17]指出,安全壳内的温度场不均匀性使得传感器布置和体积分配系数的确定具有很大不确定性,因此,掌握安全壳内流场和温度场分布情况是合理布置测温点的前提。然而,安全壳体积庞大,空间布置复杂,充气过程和稳压过程均具有强烈的非稳态特性,试验和分析方法在研究其流动与传热特性方面十分受限。而采用计算流体力学(CFD)仿真技术,不仅成本低、耗时少,还能模拟各种复杂或理想的试验过程[8],十分有助于指导安全壳整体密封性试验方法的改进和优化。但对安全壳整体密封性试验过程进行CFD 仿真模拟研究的相对较少[15,18],至今未见有研究者对全尺寸安全壳整体密封性试验的充气和稳压过程进行数值研究。
本文建立了一个安全壳及其内部构筑物的CFD 仿真模型,基于ANSYS Fluent 商用流体仿真软件,对安全壳打压(充气)试验和保压试验进行模拟,分析了其内部气体流动规律和温度分布规律。同时,本文还基于数值模拟结果,对不同测点布置方案得到的干空气质量准确性的定量研究,初步探索了提高整体试验精度的途径和方法。
1 数学物理模型
1.1 几何模型
采用简化的某安全壳模型作为研究对象,安全壳高度约为 60 m,内径为40 m。建模过程是按照标高分块,将模型分为四个主要空间:一层(标高0.00~4.00 m)、二层(4.00~7.35 m)、三层(7.35~38.00 m)及安全壳筒体(-0.50~59.88 m)。如图1 所示,安全壳空间内主要设备包含2 台蒸汽发生器、2 台冷却剂泵、1 台稳压器,构筑物隔间布置则考虑了堆坑、再生热交换器、阀门间、通风冷却口隔间、卸压箱隔间、通风机隔间、堆内构件存放池、安注箱隔间、余热排出泵隔间等。各楼层之间保留了必要的通道,确保空气流通与实际安全壳的相似性。安全壳与主要楼层隔间之间还有一个绕堆坑外墙的公用环廊区,位于层高4.63 m 处,它与蒸汽发生器隔间、主泵隔间大面积相连通。安全壳内部总体积为72 322 m3,其中,气体空间体积为63 606 m3。

图1 某安全壳简化三维几何模型Fig.1 The 3D geometric model of a simplified containment vessel
1.2 数学模型
视空气为可压缩气体,建立其三维流动与传热数学模型。主要控制方程包括连续性方程、动量方程、能量方程和湍流流动控制方程。具体如下:
连续性方程:
其中:ρ——密度;
u——速度。
动量方程:
其中:τ——黏度压力张量,Pa。
能量方程:
其中:cp——定压比热容;
T——温度;
λ——流体的传热系数;
Sr——流体的内热源及由于黏性耗散项。
湍流模型采用标准k-ε模型。标准k-ε模型需要求解湍动能及其耗散率方程,具体形式如下:
其中,μ——流体黏性系数;
μt——湍流黏性系数;
σk、σε——湍流普朗特数;
Gk——平均速度梯度所导致的湍流动能产生项;
Gb——浮力所导致的湍流动能产生项;
YM——可压缩湍流中扩张导致的波动对湍流耗散率的整体影响;
C1ε、C2ε、C3ε——湍流输运方程常数。湍流黏性系数通过k和ε计算得到:
本文取C1ε=1.44,C1ε=1.92,Cμ=0.09,湍动能k与耗散率ε的湍流普朗特数分别为σk=1.0、σε=1.3。浮力对湍流耗散率的影响程度由常数C3ε决定:
其中:vpa——平行于重力方向的速度分量;
vper——垂直于重力方向的速度分量。
Gk在标准k-ε模型和RNGk-ε模型中都是一样的表达,由湍流动能k的输运方程可以推出:
k-ε模型在k和ε方程中均考虑了浮力的影响,浮力由下式给出:
其中:Prt——湍流能量普朗特数,对于标准k-ε模型,Prt的默认值是0.85;
gi——重力在i方向上的分量;热膨胀系数β定义为:
YM通过下式计算:
其中:Mt——湍流Mach 数。
1.3 边界条件和基本假设
安全壳内初始空气的温度为300 K,压力为大气压力。整个计算过程包括80 min 充气过程,40 min 稳压过程。该过程模拟了实际打压过程第一个微小压力上升平台。充气过程的进气量为7 000 Nm3/h,进风口设置在层高y=4.2 m 处(z=0 截面经过其中心截面),定义为水平速度入口边界,送风速度和温度分别为:2.289 kg/s和300 K。进入稳压过程后,入口关闭。在充气和稳压的过程中,均不考虑任何气体出口,安全壳被假想为密闭的压力容器。考虑浮力模型,重力加速度为9.8 m/s2。
在传热方面,仅考虑充入的压缩空气与安全壳内空气之间的混合换热,不考虑气体与内部设备、隔间壁面的对流换热,即壁面取绝热。安全壳的周壁尽管会受到环境条件的影响,如风、雨、阳光等造成的外部散热或外部加热环境,但考虑安全壳壁面厚度大于1 m,这些换热对壳内空气的影响微乎其微,因此安全壳周壁也设置为绝热。
2 网格独立性验证与热力学验证
安全壳内部计算域采用非结构网格,本文采用了 ANSYS Meshing 中的四面体网格(Tetrahedrons)及Patch Conforming 算法网格划分方法,倒角处网格进行细化。第一、二、三层隔间区设备隔间布置较为复杂,因此对这些区域的网格均进行了适当加密。最终得到网格数量为43 万(模型2),默认网格大小为2.0 m,选择捕捉曲率,曲率最小尺寸为0.1 m,曲率法向角为15°;选择捕捉邻近性,邻近性最小尺寸为1.0 m,跨间隙单元格数为4。为了考察网格数量和密度对计算结果的影响,本文还采用3 万(模型1)和266 万(模型3)的网格进行相同工况的模拟,入口位置的基础均为0.05 m。
通过比较七个监测点(见图1)的温度和速度计算值来检验网格独立性。计算结果表明,其中六个点对网格密度不敏感,但位于入口上方的e1 点对网格划分方法有一定敏感性。三种网格划分方法下得到的e1 的温度随时间变化规律如图2(a)所示,显然粗网格(模型1)的结果与其他两种细网格相比,有一定偏差。为了节约计算成本与时间本文选取模型2 的网格划分方法。

图2 网格独立性验证及热力学验证Fig.2 Verification of grid independence and thermodynamics
为进一步验证网格的合适性,我们将数值计算结果与热力学分析结果进行对比。根据热力学第一定律,安全壳在打压充气期间能量方程满足式(12)[19]:
其中:m1——打压前安全壳内空气的质量;
m2——任意时刻安全壳内空气质量;
u——比热力学能;
hin——进口空气的比焓;
min——充气过程期间充入安全壳内的质量,其值为进风口质量流量与充气时间的乘积。
cvi和cpi——该时刻空气的比定容热容与比定压热容。
通过式(12)~式(15)联立可以得到不同时刻安全壳内平均温度与平均压力的理论值,将其与模型2、模型3 对应时刻的平均温度与平均压力进行对比,如图2(b)所示。由图可看出模型2 和模型3 的平均温度和平均压力相当,都与热力学计算的理论值吻合得较好。
3 安全壳内流动与传热特性分析
3.1 速度场
图3 给出了充气40 min、充气80 min 以及稳压40 min 时,安全壳内x=0 截面的速度场和流线分布。由图3(a)可以看出,受进气流影响环廊区域流动最为强烈,其次是一、二层底部空间和顶部自由空间;三层隔间连通性较差,各个隔间内气体流动均较弱。由图3(b)可以看出,当充气过程进行到80 min 时,气体流动增强的区域增多,但明显气流受到的阻力也增大;环廊仍保持了较强烈的流动,顶部大空间和一、二层隔间处则有明显的涡流。由图3(c)可以看出,稳压40 min 后安全壳内气体的流动已整体较弱,主要依靠气体浮升力的驱动,其流动方向与充气过程相反。相比顶部自由空间和环廊,一、二、三层隔间内的气体流动都较弱。根据流体特性来看,安全壳大致可分为四个不同区域:环廊区域、包含一层和二层的底部隔间区域、三层隔间区域以及顶部大空间区域。

图3 安全壳内气体速度分布和流场特征(x=0)Fig.3 Characteristics of the gas velocity distribution and the flow field in the containment (x=0)
3.2 温度场
图4 给出了三个时刻,即充气40 min、充气80 min 以及稳压40 min,安全壳内空气的温度场分布。图4(a)因为还在打压过程的中期,温度整体比后两个时刻低很多,安全壳内气体的最高温度为309 K。由图4(b)可以看出,充气80 min 时,安全壳气体温度都上升了,最高温度达到318 K。显然,这些热量的来源是充入气体带进来的焓值。同时可以看到,温度较高的区域对应了流动较弱的区域,即压缩效应更为明显的区域。图4(c)显示,稳压过程进行到足够深时,安全壳内大部分区域的温度都较为均匀,但几个分区的温度还是会有一定差异。三层隔间内温度最高,环廊区域温度最低,底部隔间区域略低于三层隔间内,顶部大空间则有分层现象。
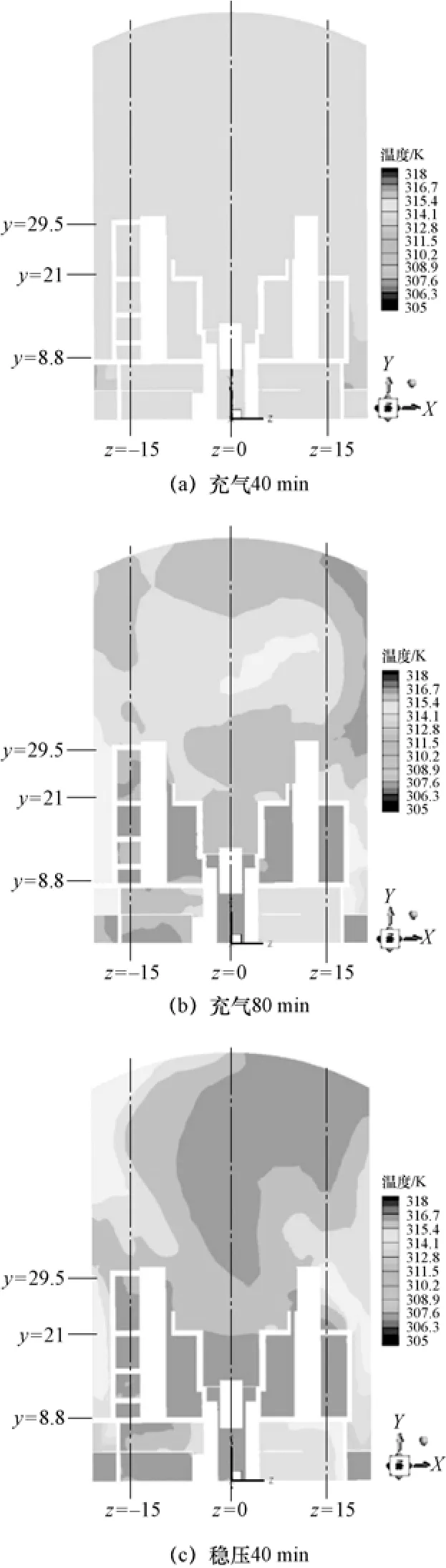
图4 安全壳内气体的温度分布(x=0)Fig.4 The temperature distribution of gas in the containment (x=0)
在x=0 截面上取z=-15 m、z=0 m、z=15 m 处,观察三个时刻空气沿高度方向的温度分布,如图5 所示。可以看到,在充气过程的早期阶段,如图5(a)所示,安全壳内大部分区域温度都较为均匀,即使有局部点温度较低,最大温差不超过0.7 ℃。当充气过程进行到80 min 后,如图5(b)所示,无论是高度方向,还是水平方向,都出现了较大的温度不均匀性,流动越弱的区域温度越高,多个截面的局部温差达到2.5 ℃左右。稳压40 min 时,如图5(c)所示,尽管流动已经较弱,但安全壳内各区域的温度仍不均匀。差异较大的区域主要体现在底部隔间和顶部,局部温差约2.0 ℃。
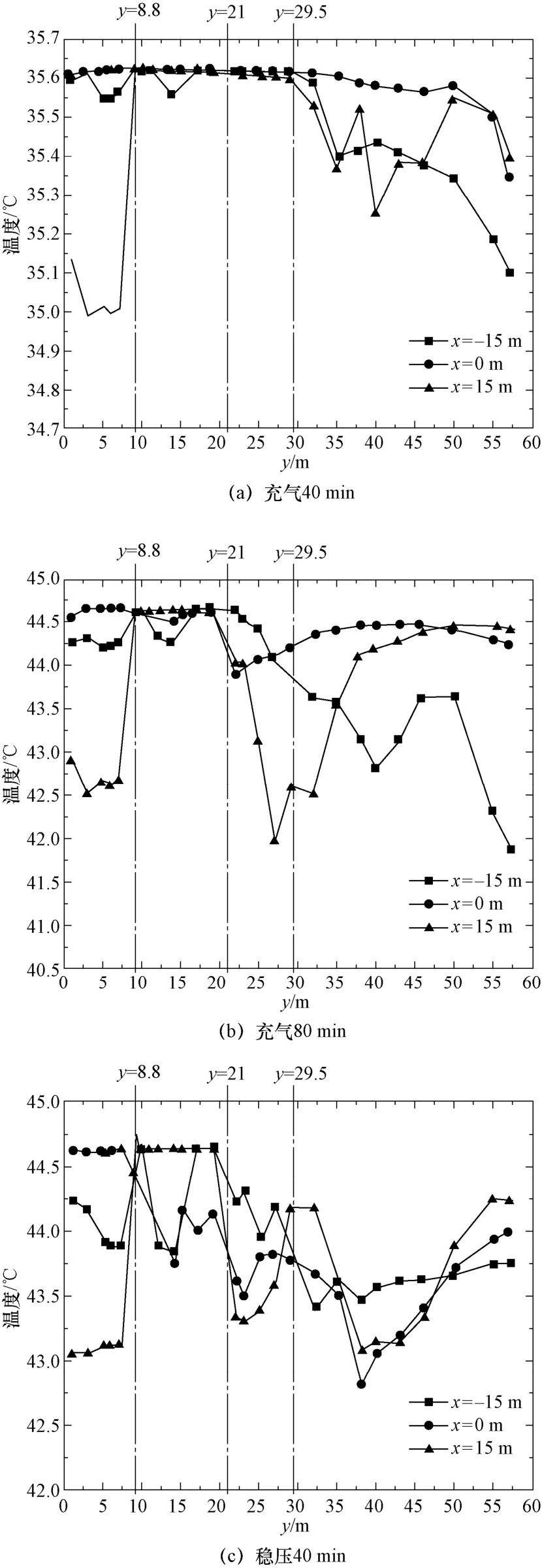
图5 安全壳内温度沿高度y 方向的分布Fig.5 The temperature distribution in the containment along y direction
4 测点布置对干空气质量计算的影响
4.1 安全壳内干空气质量的计算方法
安全壳的泄漏率不能直接测量,需要根据壳内空气质量变化间接计算。基于多点测量方法获得安全壳平均温度、平均压力,利用理想气体状态方程(16)即可获得某时刻空气质量:
式中:Pa——气体压力;
V——安全壳总自由容积;
m——任意时刻壳内干空气的总质量;
Rg——干空气的气体常数;
式中:Vi——第i个温度仪表所代表的周围自由空间气体体积;
Ti——第i个温度仪表的测量数据。
可以看出,各个仪表所代表的容积Vi的准确性直接影响到计算结果的准确性。
4.2 两种测量方案及比较
本文将基于上面的仿真结果对两种传感器布置方案的优劣进行对比,探讨安全壳内传感器布置对安全壳质量测量准确性的影响。测点当地的温度计算值被作为测量值,每个测点分配一定仪表代表容积。值得注意的是,本文的目的是探讨传感器布置的原则,因此,所提出的两种方案是结合仿真结果流场和温度场而定的较为理想的情况,并没有参考现有电站A 类试验的实际布点方案。
方案一考虑一种较为稀疏的布置方案,仅依据流场将安全壳粗略划分为7 个自由空间,每个空间设置一个温度测点,测点在安全壳的位置如图1 所示。方案二则基于温度场对这7个自由空间进行了进一步细分,设置了22 个测点。表1 以方案一为例给出了测点位置、代表空间、分配容积和容积加权因子的具体信息,图6 则进一步以面积占比表征容积占比的形式,绘制出了两种方案中各测点所代表的空间的相对位置、相对比例和彼此联通的情况。
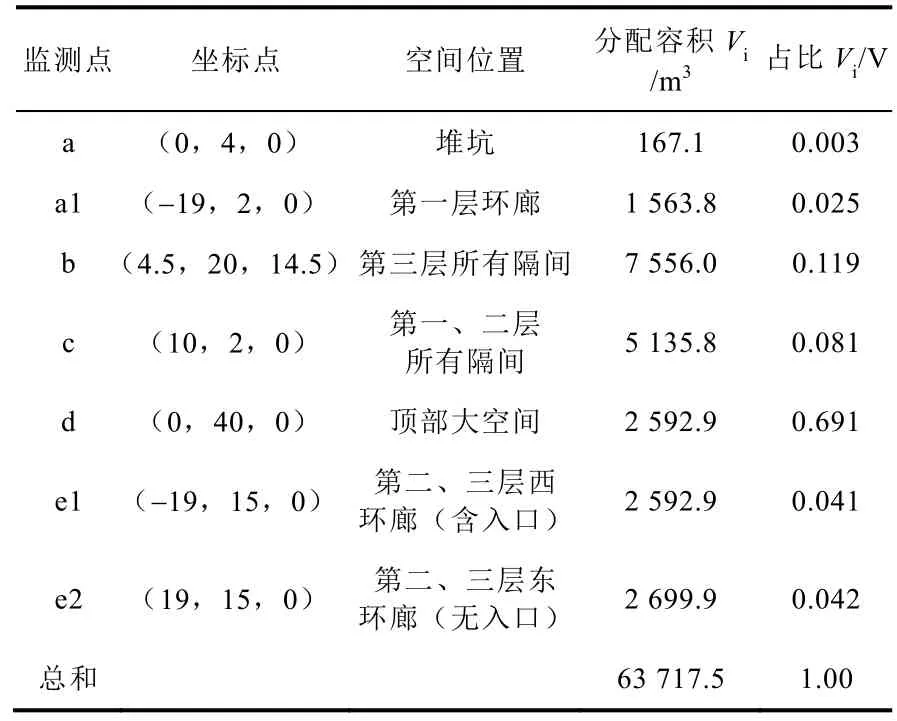
表1 七个测量点在安全壳内的位置及体积权重因子Table 1 Positions and volume weights of seven measuring points in the containment vessel
采用测量值与理论值比较的方式来评价测量值的准确性。理论值mth为通过入口进入安全壳的进气总量min和初始质量m0的总和。测量值为根据式(16)和式(17)计算得到的空气质量msim。测量误差ε定义如下:
图7 给出了不同时刻两种方案测量值的误差比较。可以看出,两种方案的测量误差都与时间有关,即受到安全壳内流动与传热过程的影响。充压阶段的测量误差随着时间先增长再降低,稳压阶段测量误差逐渐降低。大多数时刻,方案二的误差都小于方案一,但在稳压过程进行一段时间后,方案一的测量误差急剧减小,似乎更为精确。但事实上,本文计算过程中稳压阶段的空气质量理论值为常数,因此方案一的测量值并没有反映质量随时间变化的真实情况,而方案二则较好地反映了稳压过程的这一规律。综合各个时刻的情况,方案二的测量结果更为可靠。

图7 两种方案的测量值误差Fig.7 Measurement errors of the two schemes
4.3 不良测点修正的讨论
目前,对在役安全壳密封性的长期监控也是核工业界较为关注的技术研究方向。由于核电站的特殊性,仪表维护只能定期进行。因此,在役测量需要考虑局部仪表故障时的数据处理方法,一般会采用与相邻仪表代表容积合并的方法[2]。本文尝试基于仿真数据结果对合并容积的选择合理性进行探讨。
以上面给出的22 个测点的方案二为例,假设测点a1 发生仪表故障,分别选取了四种相邻仪表合并方案。其中,方案A 考虑相邻且联通原则将a1 和c 的代表容积相合并,方案B 考虑相邻且流场相似原则将a1 和a 的代表容积相合并。方案C 和方案D 都仅考虑了相邻原则,将a1 分别和e1、e4 的代表容积合并。e1 和e4 与a1 的连通性均较弱,流动和传热特性也差异较大。其中,e1 与e4 的区别是e1 中包含了空气入口。各种方案重新计算得到的干空气质量msim_i与原方案msim_22之间的偏差用 'ε表示:
图8 给出了不同时刻四种方案的测量偏差值。可以看到考虑相邻且流场相似原则的方案B 引起的测量偏差最小。考虑了相邻且连通的方案A 偏差略高,但在稳压区偏差非常稳定,因此得到的质量变化率仍是可靠性较高的。方案C 和方案D 因为合并时未考虑流场和温度场的差异,引起了较大偏差。其中方案C 因为受到入口流动的影响,在充气段引起的误差尤其大,在稳压段逐渐减小并趋于稳定。而方案D虽然在充气段小于方案C,但在稳压段偏差却较大且有波动。
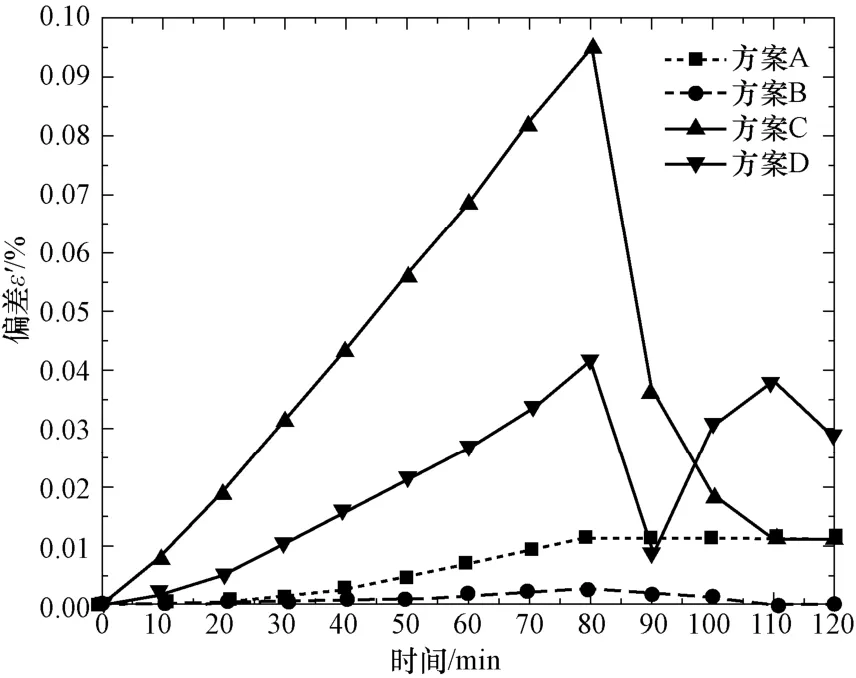
图8 关于不良测点的不同处置方案引起的测量偏差Fig.8 Measurement deviation caused by different disposal schemes for a defective measuring point
通过四种方案的比较,本文认为处理不良测点与其他测点代表容积合并时,应优先考虑相邻且流动特性相似的合并原则,在流动特性不易判断时,也可以以相邻且连通的原则。当拟合并的单元虽相邻但几乎不连通,或存在较大干扰源时,可能会引起较大的测量偏差。
5 结论
本文通过使用ANSYS Fluent 模拟安全壳内充气80 min 并静置40 min 的打压试验过程。基于仿真结果讨论了打压过程中安全壳内流场和温度场分布以及干空气质量测量方法的可靠性,得到如下结论:
(1)受壳内构筑物的影响,无论是在充气阶段还是稳压阶段,安全壳内的温度场都不均匀。稳压40 min 后,局部流动较弱的地方温度比自由空间的温度仍高2 ℃左右。
(2)空气质量测量值受测点布置和容积分配方案的影响较大。选择根据流动和温度场特性细化后的分配方案,比粗分配方案的测量误差低0.1%。
(3)对不良测点进行相邻测点容积合并时,应优先考虑相邻且流场相似原则,其次可选择相邻且联通原则。相邻但连通性较差、或有温度场干扰源的区域合并会导致较大偏差。
致谢
本研究得到了国家重点研究研发计划(No.2020YFB1901402)和中国国家自然科学基金(No.2020YFB1901402)的资助。
